РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по теории механизмов и машин
Руководитель
_______________________________
(Ф.И.О.)
Дата защиты____________________
Оценка________________________
Подпись руководителя___________
Санкт-Петербург
2011
1
.Описание работы машины и
исходные данные для проектирования.
Горизонтально-ковочная машина с вертикальным разъемом матриц
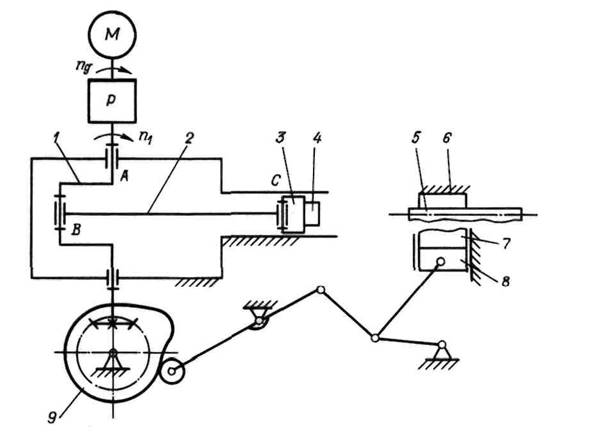
Движение передается от электродвигателя М
через редуктор Р
на кривошип 1
кривошипно-ползунного механизма (КПМ). От кривошипа через шатун 2
движение передается на ползун 3,
на котором установлен пуансон 4,
деформирующий заготовку 5, установленную в полуматрице 6.
Заготовка зажимается подвижной полуматрицей 7, установленной на зажимном ползуне 8.
Закрывание матриц происходит с помощью кулачкового механизма. Кулачок 9
получает вращение от кривошипа 1
через коническую зубчатую передачу с передаточным отношением равным единице.
Частота вращения Электродвигателя nд
= 1440 (мин-1
)
Модуль зубчатых колёс m = 2 (мм)
Момент инерции ротора двигателя Iд
= 0,06 (кг∙м2
)
Момент инерции вращающихся масс Iвр
= 0,08 (кг∙м2
)
I1А
= 0,1 (кг∙м2
)
| [s] |
ω1
(Рад/с) |
k |
υср
(м/с) |
λ |
Fmax
(н) |
| 0,05 |
10 |
3 |
0,32 |
1/3,2 |
0,01 |
2.Расчёт схемы редуктора
Цель: Подбор чисел зубьев для заданной схемы.
2.1 Определение передаточного отношения редуктора
n1
≈10∙ω1
=10∙10=100 (об/мин)
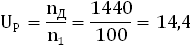
2.2 Схема редуктора
Схема состоит из двух ступеней
1-я: Простая зубчатая передача внешнего зацепления состоящая из колёс а и б
2-я: Планетарная передача состоящая из Центровых колёс 1,3
сателлита 2 и водила Н.
2.3 Разбивка передаточного отношения редуктора по ступеням.
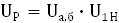
Принимаю: 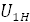 = 4 = 4
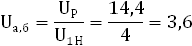
2.4 Подбор чисел зубьев по ступеням
Для подбора зубьев используем условие не подрезания зуба
zа
>17;
zб
>17;
z1
>17;
z2
>17;
z3
>85;
1) Для первой ступени 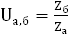
Примем z
а
=20
тогда z
б
=
z
а
∙
U
а,б
= 20 ∙ 3,6 = 72
2) Для второй ступени 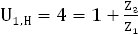
Отсюда 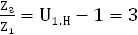
Примем z
3
=90
тогда z
1
= 30
Используя условие соостности
z3
= 2z2
+ z1
Отсюда следует z
2
=30
Предварительные итоги:
zа
=20; zб
= 72; z1
= 30; z2
= 30; z3
=90
Условие сборки 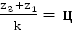 - где ц это любое целое число - где ц это любое целое число 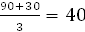
Условие соседства 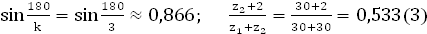
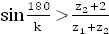
Окончательные итоги:
Реклама

z
а
=20;
z
б
= 72;
z
1
= 30;
z
2
= 30;
z
3
=90
2.5 Расчёт диаметров делительных окружностей
di
=m∙zi
dа
=40 (мм); dб
=144 (мм); d1
=60 (мм); d2
=60 (мм); d3
=180 (мм);
Схема редуктора в двух проекциях построена на листе приложений №1
3.Определение размеров звеньев КПМ
lАВ
= l1
= ? lBC
= l2
= ? h = ?
h = 2l1
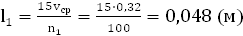
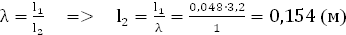
h = 2l1
= 0,096 (м)
4.Аналитический метод определения аналога скорости ползуна.
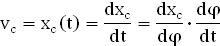
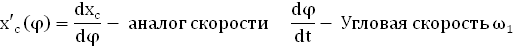
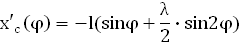
Расчёты по формуле только для рабочего хода с шагом Δφ = 30° сведены в таблицу на листе приложений №2
5.Расчёт маховика.
5.1 Определение приведённого к КПМ момента инерции
Iпр
= I1А
+ (Iд
+ Iвр
)∙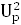
Iпр
= 0,1 + ( 0,06 + 0,08) ∙ 14,4 = 29,13
(кг∙м2
)
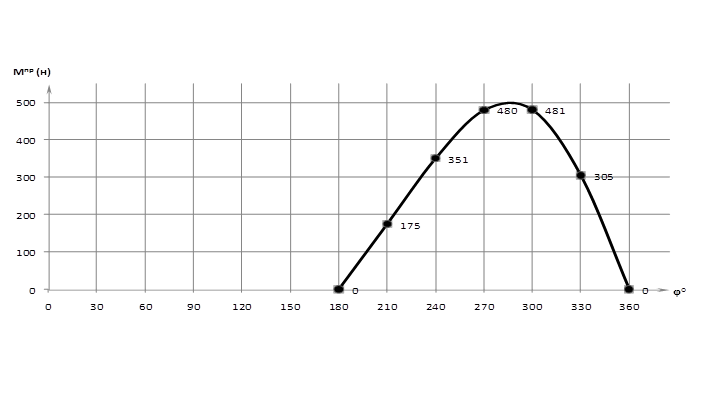
5.2 Определение приведённого момента сил полезного сопротивления
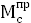 = Fmax
∙ | = Fmax
∙ | 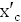 | |
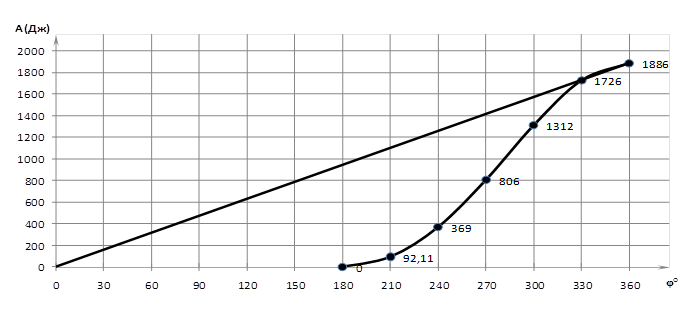
Расчёты по формуле сведены в таблицу, по ним построен график на листе приложений №2
5.3 Определение
Ac
приведённого момента сил сопротивления
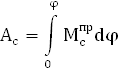
Определим интеграл численно с помощью метода трапеций
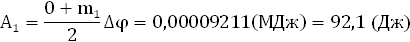
где 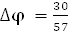
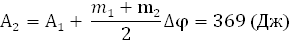
Расчёты по формуле сведены в таблицу, по ним построен график на листе приложений №2
5.4 Определение работы движущих сил
A
д
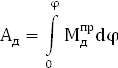
где 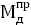 - const => - const => 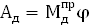 – эта прямая показана на графике на листе приложений №2 – эта прямая показана на графике на листе приложений №2
5.6 Определение максимального значения суммарной работы всех сил
Определим ΣАmax
= Ад
- Ас
графически.
С помощью графика определяем максимальное значение
ΣАmax
= 1010 (Дж) в точке φ = 210°
5.7 Определение момента инерции обеспечивающего заданное значение [
s
]
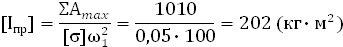
Iпр
= 29,13 кг∙м2
[Iпр
] > Iпр
следовательно нужен маховик
Iм
= [Iпр
] - Iпр
= 202-29,13= 172,87 (кг∙м2
)
Расположив маховик ДО редуктора необходимый момент инерции уменьшиться.
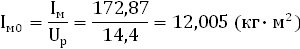
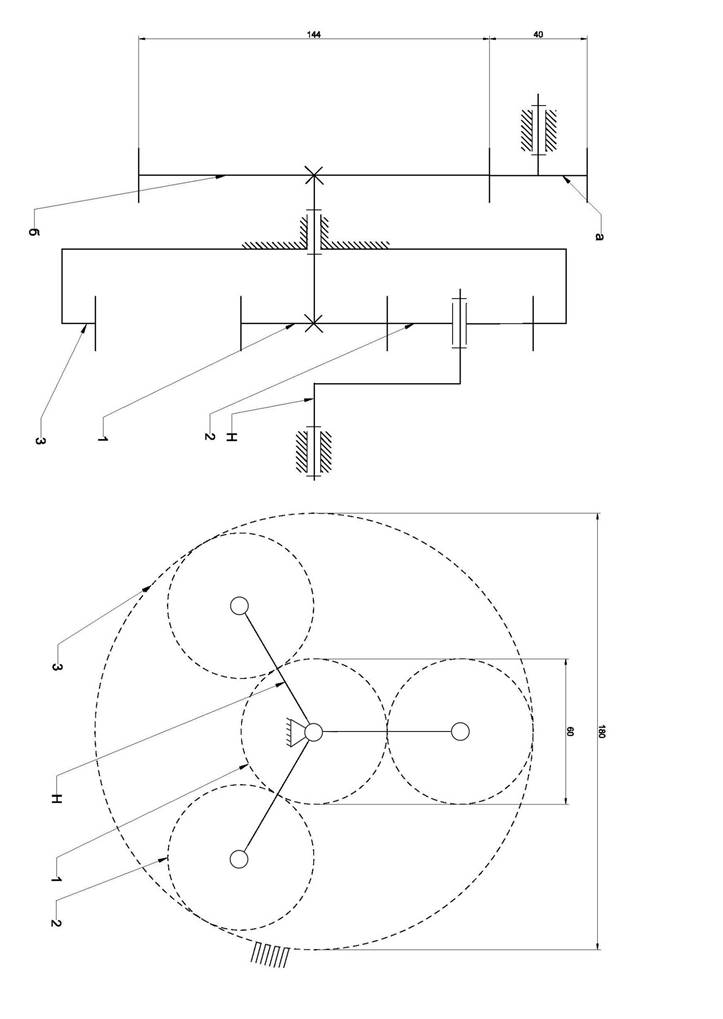 Лист приложения №1 Лист приложения №1
Лист приложения №2
| φ |
180 |
210 |
240 |
270 |
300 |
330 |
360 |
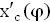 |
0,0 |
0,0175 |
0,0351 |
0,048 |
0,0481 |
0,0305 |
0,0 |
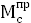 (н) (н) |
0 |
175 |
351 |
480 |
481 |
305 |
0 |
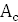 (Дж) (Дж) |
0 |
92,11 |
369 |
806 |
1312 |
1726 |
1886 |
|