Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и методики преподавания математики
Выпускная квалификационная работа
Функция Дирака
Выполнила студентка V курса
математического факультета Прокашева Е.В.
________________________________/подпись/
Научный руководитель:
старший преподаватель кафедры математического анализа и МПМ Ончукова Л.В.
________________________________/
подпись/
Рецензент:
старший преподаватель кафедры математического анализа и МПМ Фалелеева С.А.
________________________________/
подпись/
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой М.В. Крутихина
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение........................................................................................................... 3
Глава 1. Определение функции Дирака......................................................... 4
1.1. Основные понятия................................................................................ 4
1.2. Задачи, приводящие к определению дельта-функции Дирака………...10
1.2.1. Задача об импульсе ……………………………………………….10
1.2.2.Задача о плотности материальной точки……………………........11
1.3. Математическое определение дельта-функции………………………..16
Глава 2. Применение функции Дирака…………………………………………19
2.1. Разрывные функции и их производные………………………………….19
2.2. Нахождение производных разрывных функций………………………...21
Заключение………………………………………………………………………25
Введение
Развитие науки требует для ее теоретического обоснования все более и более «высокой математики», одним из достижений которой являются обобщенные функции, в частности функция Дирака. В настоящее время теория обобщенных функций актуальна в физике и математике, так как обладает рядом замечательных свойств, расширяющих возможности классического математического анализа, расширяет круг рассматриваемых задач и к тому же приводит к значительным упрощениям в вычислениях, автоматизируя элементарные операции.
Цели данной работы:
Реклама

1) изучить понятие функции Дирака;
2) рассмотреть физический и математический подходы к ее определению;
3) показать применение к нахождению производных разрывных функций.
Задачи работы: показать возможности использования дельта-функции в математике и физике.
В работе представлены различные способы определения и введения дельта-функции Дирака, ее применение при решении задач.
Глава 1
Определение функции Дирака
1.1. Основные понятия.
В разных вопросах математического анализа термин «функция» приходится понимать с разной степенью общности. Иногда рассматриваются непрерывные, но не дифференцируемые функции, в других вопросах приходится предполагать, что речь идет о функциях, дифференцируемых один или несколько раз и т.д. Однако в ряде случаев классическое понятие функции, даже трактуемое в самом широком смысле, т.е. как произвольное правило, относящее каждому значению x из области определения этой функции некоторое число y=f(x),оказывается недостаточным.
Вот важный пример: применяя аппарат математического анализа к тем или иным задачам, нам приходится сталкиваться с таким положением, когда те или иные операции анализа оказываются невыполнимыми; например, функцию, не имеющую производной (в некоторых точках или даже всюду), нельзя дифференцировать, если производную понимать как элементарную функцию. Затруднений такого типа можно было бы избежать, ограничившись рассмотрением одних только аналитических функций. Однако такое сужение запаса допустимых функций во многих случаях весьма нежелательно. Необходимость дальнейшего расширения понятия функции стала особенно острой.
В 1930 году для решения задач теоретической физики крупнейшему английскому физику-теоретику П. Дираку, одному из основателей квантовой механики, не хватило аппарата классической математики, и он ввел новый объект, названный “дельта-функцией”, который выходил далеко за рамки классического определения функции.
П. Дирак в книге «Принципы квантовой механики» [5] определил дельта-функцию δ(x) следующим образом:
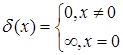 . .
Кроме того задается условие:
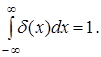
Наглядно можно представить график функции, похожей на δ(x), как показано на рисунке 1. Чем более у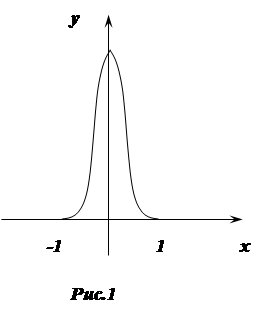 зкой сделать полоску между левой и правой ветвью, тем выше должна быть эта полоска, для того чтобы площадь полоски (т.е. интеграл) сохраняла свое заданное значение, равное 1. При сужении полоски мы приближаемся к выполнению условия δ(
x
) = 0
при x
≠ 0
, функция приближается к дельта-функции. зкой сделать полоску между левой и правой ветвью, тем выше должна быть эта полоска, для того чтобы площадь полоски (т.е. интеграл) сохраняла свое заданное значение, равное 1. При сужении полоски мы приближаемся к выполнению условия δ(
x
) = 0
при x
≠ 0
, функция приближается к дельта-функции.
Реклама

Такое представление общепринято в физике.
Следует подчеркнуть, что δ(
x
)
не является функцией в обычном смысле, так как из этого определения следуют несовместимые условия с точки зрения классического определения функции и интеграла:
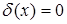 при
при 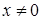 и и 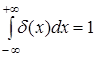 . .
В классическом анализе не существует функции, обладающей свойствами, предписанными Дираком. Лишь несколько лет спустя в работах С.Л. Соболева и Л. Шварца дельта-функция получила свое математическое оформление, но не как обычная, а как обобщенная функция.
Прежде чем переходить к рассмотрению функции Дирака, введем основные определения и теоремы, которые нам будут необходимы:
Определение 1.Изображением функцииf(t) или L - изображением заданной функции f(t) называют функцию комплексной переменной p,определяемую равенством:
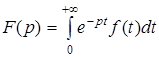
При этом будем считать, что при t
<0
f
(
t
)=0
, а при t
>0
выполняется неравенство 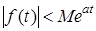 , где М
и а
– некоторые положительные постоянные. , где М
и а
– некоторые положительные постоянные.
Определение 2.
Функция f
(
t
)
, определенная так:
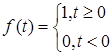 , ,
 называется единичной функцией Хевисайда
и обозначается через называется единичной функцией Хевисайда
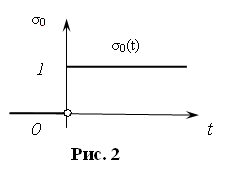
и обозначается через 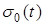 . График этой функции изображен на рис.2 . График этой функции изображен на рис.2
Найдем L
– изображение функции Хевисайда:
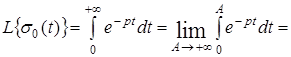
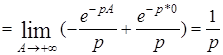 . .
Итак,
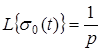 (1) (1)
Пусть функция f(t) при t<0 тождественно равна нулю (рис.3). Тогда функция f(t-t0
) будет тождественно равна нулю при t<t0
(рис.4).
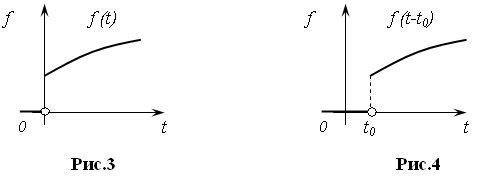
Для нахождения изображения δ(x) с помощью вспомогательной функции рассмотрим теорему запаздывания:
Теорема 1.
Если
F
(
p
) есть изображение функции
f
(
t
), то 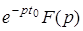 есть изображение функции
f
(
t
-
t
0
), то есть если
L
{
f
(
t
)}=
F
(
p
), то есть изображение функции
f
(
t
-
t
0
), то есть если
L
{
f
(
t
)}=
F
(
p
), то
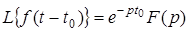 . .
Доказательство.
По определению изображения имеем
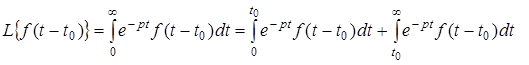 .
.
Первый интеграл равен нулю, так как f
(
t
-
t
0
)=0
при t
<
t
0
. В последнем интеграле сделаем замену переменной t
-
t
0
=
z
:
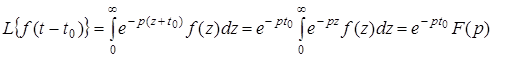 . .
Таким образом, 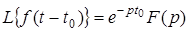 . .
Для единичной функции Хевисайда было установлено, что 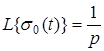 . На основании доказанной теоремы следует, что для функции
. На основании доказанной теоремы следует, что для функции 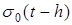 , L
–
изображением будет , L
–
изображением будет 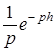 , то есть , то есть
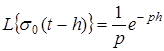 (2)
(2)
Определение 3.
Непрерывная или кусочно-непрерывная функция δ(
t
,
λ
)
аргумента t
, зависящая от параметра λ
, называется иглообразной
, если:
1) 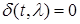 при при 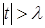 ; ;
2) 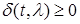 при при 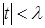 ; ;
3) 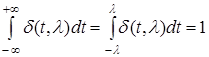
Определение 4.
Числовую функцию f
, определенную на некотором линейном пространстве L
, называют функционалом
.
Зададим совокупность тех функций, на которых будут действовать функционалы. В качестве этой совокупности рассмотрим множество K
всех вещественных функций φ(
x
)
, каждая из которых имеет непрерывные производные всех порядков и финитна, то есть обращается в нуль вне некоторой ограниченной области (своей для каждой из функций φ(
x
)
). Эти функции будем называть основными
, а всю их совокупность К
– основным пространством
.
Определение 5
. Обобщенной функцией
называется всякий линейный непрерывный функционал, определенный на основном пространстве К
.
Расшифруем определение обобщенной функции:
1) обобщенная функция f
есть функционал на основных функциях φ
, то есть каждой φ
сопоставляется (комплексное) число (
f
, φ)
;
2) функционал f
линейный, то есть 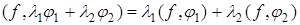 для любых комплексных чисел λ1
и λ2
и любых основных функций φ1
и φ2
; для любых комплексных чисел λ1
и λ2
и любых основных функций φ1
и φ2
;
3) функционал f
непрерывный, то есть 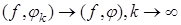 , если , если 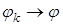 . .
Определение 6.
Импульс
– одиночный, кратковременный скачок электрического тока или напряжения[2, стр. 482].
Определение 7.
Средняя плотность
– отношение массы тела m
к его объему V
, то есть 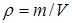 [2, стр. 134]. [2, стр. 134].
Теорема 2.
(Обобщенная теорема о среднем).
Если
f
(
t
) – непрерывная, а 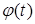 - интегрируемая функции на [
a
;
b
], причем - интегрируемая функции на [
a
;
b
], причем 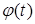 на этом отрезке не меняет знака, то на этом отрезке не меняет знака, то 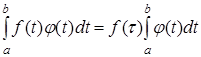 , где , где 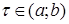 [1, стр. 228].
[1, стр. 228].
Теорема 3.
Пусть функция
f
(
x
), ограничена на [
a
,
b
] и имеет не более конечного числа точек разрыва. Тогда функция
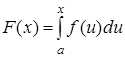 является первообразной для функции
f
(
x
) на отрезке [
a
,
b
] и для любой первообразной Ф(
x
) справедлива формула
является первообразной для функции
f
(
x
) на отрезке [
a
,
b
] и для любой первообразной Ф(
x
) справедлива формула 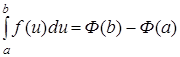 [1, стр. 220].
[1, стр. 220].
Определение 8.
Совокупность всех непрерывных линейных функционалов, определенных на некотором линейном пространстве Е
, образует линейное пространство. Оно называется пространством, сопряженным
с Е
, и обозначается Е*
.
Определение 9.
Линейное пространство Е
, в котором задана некоторая норма, называется нормированным пространством
.
Определение 10.
Последовательность 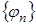 называется слабо сходящейся
к называется слабо сходящейся
к 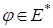 , если для каждого , если для каждого 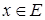 выполнено соотношение выполнено соотношение 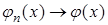 . .
Теорема 4.
Если {
xn
} – слабо сходящаяся последовательность в нормированном пространстве, то существует такое постоянное число С, что 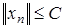 [10, стр. 187].
[10, стр. 187].
1.2 Задачи, приводящие к определению дельта-функции Дирака.
С физической точки зрения, функция Дирака, применяемая в математической физике при решении задач, в которые входят сосредоточенные в одной точке величины (нагрузка, заряд и т. п.), представлена как простейшая обобщенная функция, позволяющая записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в точке a
пространства Rn
. Она характеризует, например, плотность распределения масс, при котором в одной точке сосредоточена единичная масса, а любой интервал, не содержащий этой точки, свободен от масс.
1.2.1.Задача об импульсе.
Рассмотрим функцию
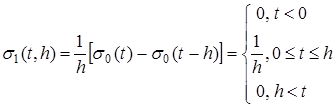 , ,
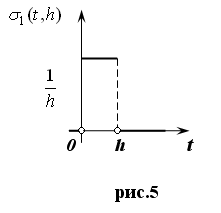
изображенную на рис.5.
Если эту функцию трактовать как силу, действующую за промежуток времени от 0
до h
, а в остальное время равную нулю, то импульс этой силы, вычисляемый по формуле 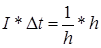 равен единице. равен единице.
На основании формул (1) и (2) изображение этой функции будет
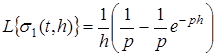
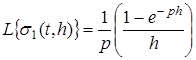 . .
В механике бывает удобно рассматривать силы, действующие очень короткий промежуток времени, как силы, действующие мгновенно, но имеющие конечный импульс. Поэтому вводят функцию δ(
t
)
как предел функции 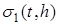 при при 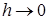 : :
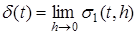 . .
Эту функцию называют единичной импульсной функцией
или дельта-функцией
, причем 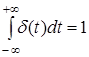 , так как импульс силы равен единице. , так как импульс силы равен единице.
1.2.2. Задача о плотности материальной точки.
Попытаемся определить плотность, создаваемую материальной точкой массы 1.
Положим, что эта точка есть начало координат. Чтобы определить плотность, распределим единичную массу равномерно внутри шара радиуса ε
с центром в 0
. В результате получим среднюю плотность fε
(
x
)
, равную
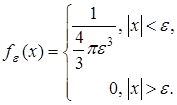
Но нас интересует плотность при 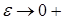 (т.е. ε
стремится к 0
справа). Примем сначала в качестве искомой плотности δ(
x
)
предел последовательности средних плотностей fε
(
x
)
при (т.е. ε
стремится к 0
справа). Примем сначала в качестве искомой плотности δ(
x
)
предел последовательности средних плотностей fε
(
x
)
при 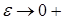 , то есть функцию , то есть функцию
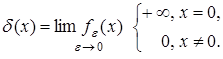 (3) (3)
От плотности δ
естественно требовать, чтобы интеграл от нее по всему пространству давал бы полную массу вещества, то есть
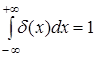 . (4) . (4)
Но для функции δ(
x
)
, определенной формулой (3), 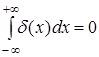 . Это значит, что функция не восстанавливает массу (не удовлетворяет требованию (4)) и поэтому не может быть принята в качестве искомой плотности. Таким образом, предел последовательности средних плотностей fε
(
x
)
не подходит для наших целей, то есть не может быть принят в качестве плотности δ(
x
)
. . Это значит, что функция не восстанавливает массу (не удовлетворяет требованию (4)) и поэтому не может быть принята в качестве искомой плотности. Таким образом, предел последовательности средних плотностей fε
(
x
)
не подходит для наших целей, то есть не может быть принят в качестве плотности δ(
x
)
.
Для любой непрерывной функции φ(
x
)
найдем слабый предел последовательности 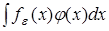 при при 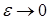 . .
Покажем, что
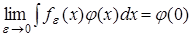 (5)
(5)
Действительно, в силу непрерывности функции φ(
x
)
для любого η>0
существует такое ε0
>0
, что 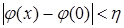 , коль скоро , коль скоро 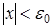 . Отсюда при всех . Отсюда при всех 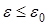 получаем получаем
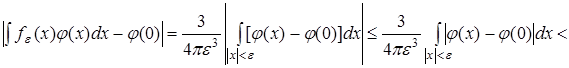
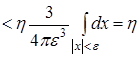 . .
Покажем, что 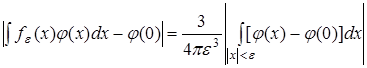 . .
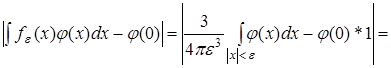
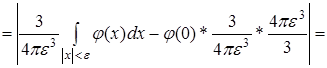
Так как 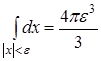 (здесь dx
фактически равен dV
), то (здесь dx
фактически равен dV
), то 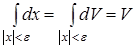 - объем шара радиуса ε
. Следовательно, - объем шара радиуса ε
. Следовательно,
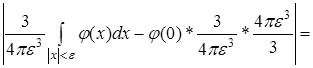
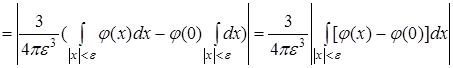 . .
Формула (5) обозначает, что слабым пределом последовательности функций fε
(
x
)
, 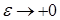 , является функционал φ(0)
(а не функция!), сопоставляющий каждой непрерывной функции φ(
x
)
число φ(0)
– ее значение в точке x
=0
. Этот функционал принимается за определение плотности δ(
x
)
– это и есть дельта-функция Дирака. Итак, можно записать
, является функционал φ(0)
(а не функция!), сопоставляющий каждой непрерывной функции φ(
x
)
число φ(0)
– ее значение в точке x
=0
. Этот функционал принимается за определение плотности δ(
x
)
– это и есть дельта-функция Дирака. Итак, можно записать
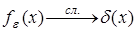 , , 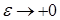 , ,
понимая под этим предельное соотношение (5). Значение функционала δ
на функции φ
– число φ(0)
– обозначается так:
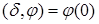 (6)
(6)
Это равенство дает точный смысл дельта-функции, введенной Дираком, обладающей следующими свойствами:
δ(
x
)=0,
x
≠0, 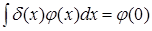 , ,
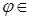 C
. C
.
Роль интеграла 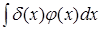 здесь играет величина здесь играет величина 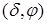 - значение функционала δ
на функции φ
.
- значение функционала δ
на функции φ
.
Таким образом, дельта-функция - функционал, сопоставляющий по формуле 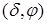 =φ(0) каждой непрерывной функции φ число φ(0)- ее значение в нуле. =φ(0) каждой непрерывной функции φ число φ(0)- ее значение в нуле.
Проверим, что функционал δ
восстанавливает полную массу. Действительно, роль интеграла 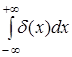 играет величина играет величина 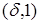 , равная, в силу (6), значению функции, тождественно равной 1, в точке x=0, то есть
, равная, в силу (6), значению функции, тождественно равной 1, в точке x=0, то есть 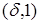 =1(0)=1
. =1(0)=1
.
Таким образом, плотность, соответствующая точечному распределению масс, не может быть описана в рамках классического понятия функции, и для ее описания следует привлекать линейные (непрерывные) функционалы.
1.3
.Математическое определение функции Дирака.
Функция δ(
x
)
применяется не только в механике, а во многих разделах математики, в частности при решении многих задач уравнений математической физики.
Пусть f
(
t
)
- функция, непрерывная на (
a
;
b
)
, а 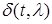 - иглообразная функция. Для дальнейшего введения определения дельта-функции Дирака рассмотрим поведение интеграла - иглообразная функция. Для дальнейшего введения определения дельта-функции Дирака рассмотрим поведение интеграла
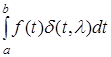 при
при 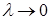
Рассмотрим (
a
;
b
)
, содержащий внутри себя точку t
=0
, то есть a
<0<
b
и 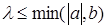 . Из определения иглообразной функции и обобщенной теоремы о среднемполучаем: . Из определения иглообразной функции и обобщенной теоремы о среднемполучаем:
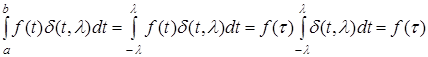 , где , где 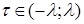 . .
Если 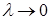 , то и , то и 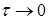 , а в силу непрерывности функции f
(
t
)
и , а в силу непрерывности функции f
(
t
)
и 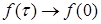 . Поэтому при a
<0<
b . Поэтому при a
<0<
b
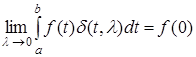 (7)
(7)
Если же числа a
и b
одинаковых знаков (a
<
b
<0
или 0<
a
<
b
), то есть (
a
;
b
)
не содержит внутри себя точки t
=0
, то

при всех достаточно малых λ
.
Если числа a
и b
имеют одинаковые знаки, то при 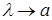 , если a
>0
(рис.6), или при , если a
>0
(рис.6), или при 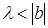 , если b
<0
(рис.7), интервал , если b
<0
(рис.7), интервал 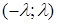 не будет пересекаться с (
a
;
b
)
, а поэтому для всех не будет пересекаться с (
a
;
b
)
, а поэтому для всех 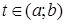
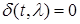 и
и 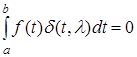 . .
Следовательно,
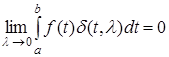 (8) (8)
Введём обозначение: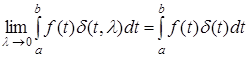 (9)
(9)
Таким образом, δ(
t
)
– обобщенная функция, характеризующая предельное поведение иглообразной функции 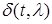 при при 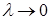 и использующаяся при вычислении интегралов. и использующаяся при вычислении интегралов.
Дельта-функцию можно применять и формально, пользуясь лишь следующим ее основным свойством
, вытекающим из равенств (7) - (9) для любой непрерывной функции.
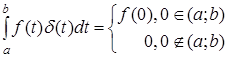 (10)
(10)
Введем подстановку 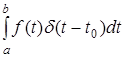 = = 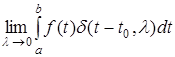 , то , то
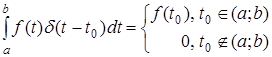 (11)
(11)
Свойство, описываемое соотношениями (10) и (11) называют фильтрующим свойством
дельта-функции.
При f
(
t
)≡1
соотношения (9) – (11) принимают вид
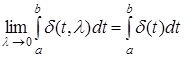

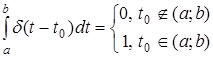
Если за интервал (
a
;
b
)
взять всю числовую ось, то 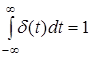 . .
Глава 2
Применение функции Дирака
2.1. Разрывные функции и их производные.
XX - XI век находит много конструктивных решений для того, что казалось невозможным в XIX веке. Так дельта-функция решает вопрос о производной в точке разрыва (в частности, для разрыва, имеющего вид конечного скачка).
 Рассмотрим интеграл функции δ
(
x
)
в зависимости от его верхнего предела, то есть функцию Рассмотрим интеграл функции δ
(
x
)
в зависимости от его верхнего предела, то есть функцию
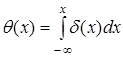 . (12) . (12)
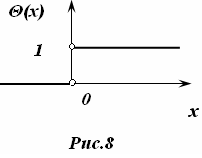
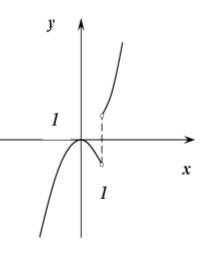
График этой функции имеет вид «ступеньки» (рис.8). Пока x
<0
, область интегрирования в формуле (12) целиком находится там, где δ
(
x
)=0
. Следовательно, θ
(
x
)=0
при x
<0
. Если же x
>0
, то при интегрировании включается окрестность начала координат, где 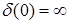 . С другой стороны, так как приx
>0
также δ
(
x
)=0
, то значение интеграла не изменяется, когда верхний предел меняется от 0,1
до 1
, или до 10
, или до ∞
. Следовательно, при x
>0
имеем . С другой стороны, так как приx
>0
также δ
(
x
)=0
, то значение интеграла не изменяется, когда верхний предел меняется от 0,1
до 1
, или до 10
, или до ∞
. Следовательно, при x
>0
имеем
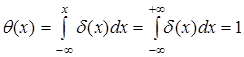
как и показано на рис.8.
Таким образом, с помощью дельта-функции сконструирована простейшая разрывная функция θ
(
x
)
такая, что при x
<0
, θ
(
x
)=0
, а в области x
>0
, θ
(
x
)=1
. При x=0
, θ
терпит разрыв от 0
до 1
.
Не зная дельта-функции, приходится говорить, что производную нельзя находить там, где функция разрывна. Мы построили разрывную функцию θ
(
x
)
. По теореме о существовании первообразной для ограниченной функции, имеющей конечное или счетное число точек разрыва, общее правило связи между интегралом и производной имеет вид:
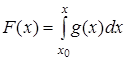 . .
Тогда 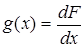 . .
Применим его к выражению (12), получим
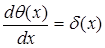 . .
Значит, для производной разрывной функции не надо делать исключений: просто в точке разрыва производная равна «особенной» функции – дельта-функции Дирака.
Производная разрывной функции определяется следующим образом:
f
’(
x
)={
f
’(
x
)}+[
fx
0
]
δ
(
x
–
x
0
)
,
где fx
0
– величина разрыва в точке x
0
,
{
f
’(
x
)}
– производная везде, кроме точки x
0
.
Благодаря дельта-функции Дирака можно найти производные в более сложных случаях.
2.2. Нахождение производных разрывных функций.
Пример 1: Найти производную функции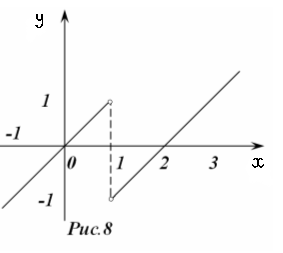
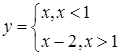 . .
График функции рис.8. Разрыв имеет место при x
=1
. Величина разрыва y
(1+0)-
y
(1-0) =1-2-1= -2
, где
y
(1+0)
– это предельное значение y
при приближении x
к 1
справа (со стороны x
>1
), y
(1 - 0)
– то же слева. Отсюда получаем, что
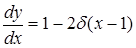 (13) (13)
 Такая запись лучше утверждения, что Такая запись лучше утверждения, что 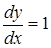 везде, кроме точки x
=1
, где функция терпит разрыв и не имеет производной. В записи (13) в одной строчке содержится и факт разрыва (раз вошла δ
), и место его (x
=1
), и величина (коэффициент (- 2) при δ
). везде, кроме точки x
=1
, где функция терпит разрыв и не имеет производной. В записи (13) в одной строчке содержится и факт разрыва (раз вошла δ
), и место его (x
=1
), и величина (коэффициент (- 2) при δ
).
Пример 2:
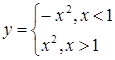 . .
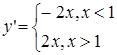 . .
Разрыв в точке x
=1
. Величина разрыва: y
(1+0)-
y
(1 - 0)=2
. Теперь мы можем точку х=1
присоединить к левой области и тогда написать
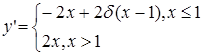 . .
Либо другой вариант – можно присоединить х=1
к правой области и тогда с равным правом запишем
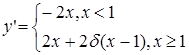 . .
Можно написать также
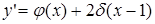 , ,
где 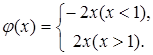
Пример 3:
Рассмотрим модель прохождения тока вдоль цепи, представленную в работе М.Н. Дубайловой «Применение рядов Фурье при решении задач Электродинамики» [7].
Найдем производную данной функции, представленной графиком зависимости силы тока от времени:
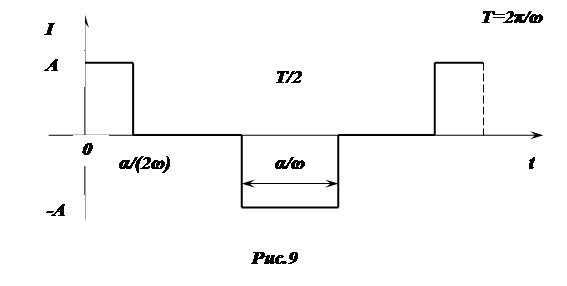
По графику видно, что сила тока в точках α/(2ω)
, 2π-α/(2ω)
, 2π+α/(2ω)
, 4π-α/(2ω)
,… мгновенно падает от А
до 0
или от 0
до –А
, то есть ток мгновенно становится равным 0
, и вновь появляется с отрицательным значением. Исчезновение тока в цепи означает, что цепь разрывается, поэтому в реальном процессе снова появится через какое-то время ток самопроизвольно не может. Такая модель прохождения тока вдоль цепи является противоречивой.
В действительности сила тока меняется не мгновенно, а в течение короткого конечного промежутка времени. Реальный процесс можно изобразить следующим графиком (рис.10).
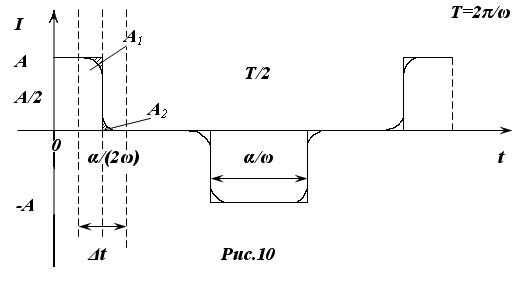
В физике используется упрощенная модель, график которой представлен на рис.9, так как работа силы тока в коротком конечном промежутке времени Δ
t
равна нулю (A
=
 =
A
1
+
A
2
=
A
1
+(-
A
1
)=0
, геометрически числа A
1
и A
2
выражают площади заштрихованных фигур, см. рис.10).
=
A
1
+
A
2
=
A
1
+(-
A
1
)=0
, геометрически числа A
1
и A
2
выражают площади заштрихованных фигур, см. рис.10).
В математике рис.9 не является графиком функции (одному значению t
соответствует бесконечное множество значений I
). Поэтому математика рассматривает упрощенную модель, абстрагированную от реального процесса, разрывая функцию, график этой модели представлен на рис.11.
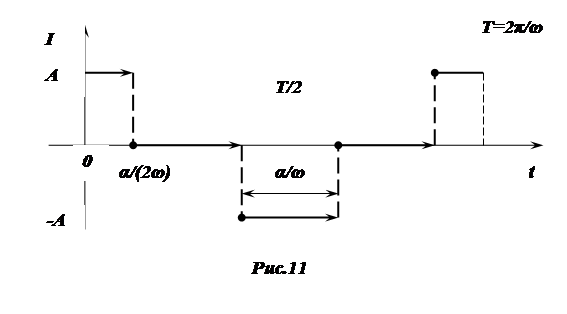 
Найдем производную данной функции.
Для этого функцию зададим следующим образом:
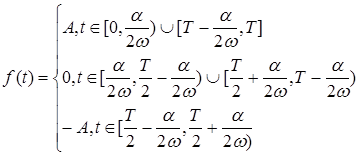 . .
Разрывы имеют место при 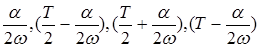 . .
Величины разрывов равны –
A
, -
A
,
A
,
A
соответственно. Отсюда получаем, что
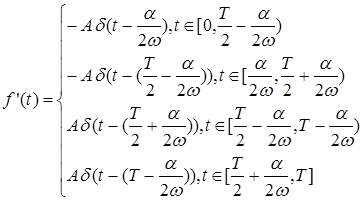 . .
Заключение
В выпускной квалификационной работе поставленные цели достигнуты, то есть были достаточно подробно рассмотрены математический и физический подходы к определению функции Дирака, причем физический подход к определению осуществлен через решение физических задач об импульсе и плотности материальной точки. Применение функции Дирака для нахождения производных разрывных функций было проиллюстрировано с помощью математических и физических примеров, выявлена целесообразность применения дельта-функции для нахождения производных разрывных функций. Теоретический материал подтверждается решением различных примеров.
Таким образом, функция Дирака – одно из наиболее необходимых и широко применяемых понятий, как в физике, так и в математическом анализе.
Библиографический список
1. Архипов, Г.И. Лекции по математическому анализу [Текст]: учебник для университетов и пед. вузов / Г.И. Архипов, В.А. Садовничий, В.Н. Чубариков. Под ред. В.А. Садовничего. – М.: Высш. шк., 1999.
2. Большая советская энциклопедия [Текст] / Гл. ред. А.М. Прохоров. – М.: Советская энциклопедия, 1972.
3. Бронштейн, И.Н. Справочник по математике [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 1967.
4. Владимиров, В.С. Обобщенные функции и их применение [Текст] / В.С. Владимиров. – М.: Знание, 1990.
5. Владимиров, В.С. Обобщенные функции в математической физике[Текст] / В.С. Владимиров. – М.: Наука, 1981.
6. Дирак, П. Принципы квантовой механики [Текст]/ П.Дирак. - М.: Наука, 1979.
7. Дубайлова, М.Н. Применение рядов Фурье при решении задач Электродинамики [Текст] / Выпускная квалификационная работа. – Киров, ВГГУ 2003.
8. Ершова, В.В. Импульсные функции. Функции комплексной переменной. Операционное исчисление [Текст] / В.В. Ершова. Под ред. В.И. Азаматовой. - Минск: Вышэйш. школа, 1976.
9. Зельдович, Я.Б. Высшая математика для начинающих [Текст] / Я.Б. Зельдович. – М.: Наука, 1970.
10. Колмогоров, А.Н. Элементы теории функций и функционального анализа [Текст] / А.Н. Колмогоров, С.В. Фомин. – М.: Наука, 1972.
11. Пискунов, Н.С. Дифференциальное и интегральное исчисления [Текст] / Н.С. Пискунов // учеб. для втузов. В 2-х т. Т. II: - М.: Интеграл-Пресс, 2001.
12. Соболев, В.И. Лекции по дополнительным главам математического анализа [Текст] / В.И. Соболев. – М.: Наука, 1968.
|