Математический факультет
Кафедра информатики и прикладной математики
КУРСОВАЯ РАБОТА НА ТЕМУ:
«УМЕНЬШЕНИЕ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА»
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
3. ОКНА ПРОСМОТРА ДАННЫХ
ЗАКЛЮЧЕНИЕ
СПИСОКИСПОЛЬЗОВАННЫХИСТОЧНИКОВ
ПРИЛОЖЕНИЕ
 ВВЕДЕНИЕ
ВВЕДЕНИЕ
Почти в каждой области встречаются явления, которые интересно и важно изучать в их развитии и изменении во времени. В повседневной жизни могут представлять интерес, например, метеорологические условия, цены на тот или иной товар, те или иные характеристики состояния здоровья индивидуума и т.п. Все они изменяются во времени. Совокупность измерений какой-либо одной характеристики подобного рода и представляет собой временной ряд.
Одной из главных задач спектрального анализа временных рядов является построение и исследование оценок спектральных плотностей стационарных случайных процессов, так как они дают важную информацию о структуре процесса.
Методы анализа временных рядов широко используются в различных областях науки и техники, их можно применять при анализе больших объемов данных, получаемых в процессе вибрационных испытаний или извлекаемых из сводок экономических данных.
В данной работе исследована оценка спектральной плотности, построенная с использованием различных окон просмотра данных. Построены графики этой оценки для временного ряда, представляющего собой последовательность наблюдений - температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
Графики построены также для центрированного случайного процесса.
 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
Векторным временным рядом
(r-мерным временным рядом) называется совокупность функций вида
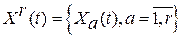 . .
Переменная t обычно соответствует времени выполнения или регистрации наблюдений и измерений.
Действительным случайным процессом
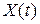 = = 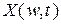 называется семейство случайных величин, заданных на вероятностном пространстве называется семейство случайных величин, заданных на вероятностном пространстве 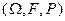 , где , где 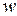 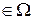 , , 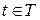 , , 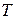 - некоторое параметрическое множество. - некоторое параметрическое множество.
Если 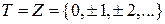 , или , или 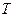 - подмножество из - подмножество из 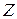 , то говорят, что , то говорят, что 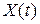 , , 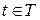 - случайный процесс с дискретным временем
. - случайный процесс с дискретным временем
.
Если 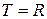 , или , или 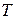 подмножество из подмножество из 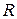 , то говорят, что , то говорят, что 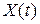 , , 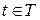 - случайный процесс с непрерывным временем. - случайный процесс с непрерывным временем.
Реклама

Введем характеристики случайного процесса 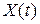 , , 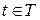 , во временной области. , во временной области.
Математическим ожиданием
случайного процесса 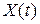 , , 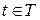 , называется функция вида , называется функция вида
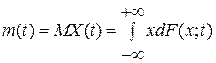 , ,
где 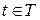 . .
Дисперсией
случайного процесса 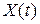 , , 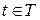 , называется функция вида , называется функция вида
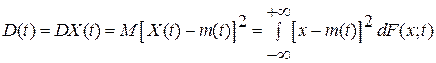 , ,
где 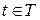 . .
Спектральной плотностью
случайного процесса 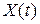 , , 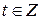 , называется функция вида , называется функция вида
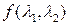 = =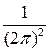 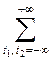 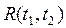 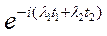 , ,
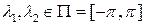 , ,
при условии, что
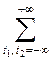 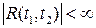 . .
Нормированной спектральной плотностью
случайного процесса 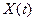 называется функция вида называется функция вида
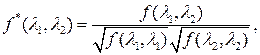
где 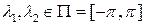 , если , если 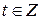 и и 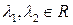 , если , если 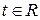 . .
Из определения видно, что спектральная плотность 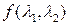 непрерывная, периодическая функция с периодом, равным непрерывная, периодическая функция с периодом, равным 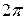 по каждому из аргументов. по каждому из аргументов.
Ковариационной функцией
случайного процесса 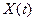 , , 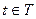 , называется функция вида , называется функция вида
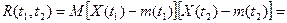 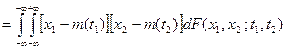 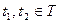 . .
Смешанным моментом 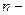 го порядка
, го порядка
, 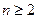 , случайного процесса , случайного процесса 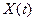 , , 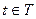 , называется функция вида , называется функция вида
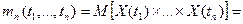 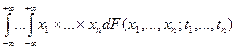 , , 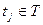 , , 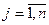 . .
Заметим, что
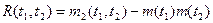 , ,
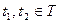 . .
Лемма 1.1.
Для любого целого р справедливо следующее соотношение
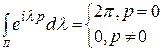 . .
Доказательство.
Если 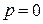 , то доказательство очевидно. Рассмотрим случай , то доказательство очевидно. Рассмотрим случай 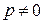 . Воспользуемся формулой Эйлера . Воспользуемся формулой Эйлера
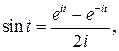
тогда
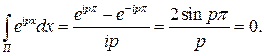
Лемма доказана.
Пусть 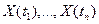 - значения случайного процесса - значения случайного процесса 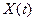 в точках в точках 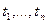 . Введем функцию . Введем функцию
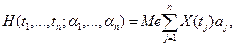 , ,
которую будем называть характеристической функцией
, где 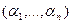 - ненулевой действительный вектор, - ненулевой действительный вектор, 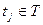 , , 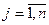 . .
Смешанный момент 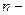 го порядка
, го порядка
, 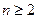 , можно также определить как , можно также определить как
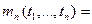 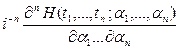 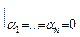 , , 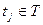 , , 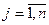 . .
Смешанным семиинвариантом (кумулянтом) 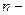 го порядка
, го порядка
, 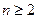 , случайного процесса , случайного процесса 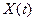 , , 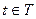 , называется функция вида , называется функция вида
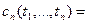 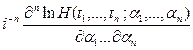 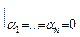 , , 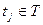 , , 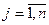 , ,
которую также будем обозначать как 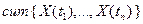 . .
Между смешанными моментами и смешанными семиинвариантами 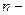 го порядка, го порядка, 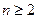 , существуют связывающие их соотношения, которые имеют вид , существуют связывающие их соотношения, которые имеют вид
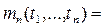 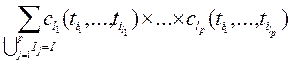 , ,
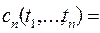 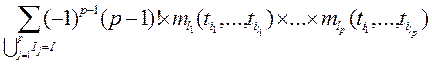 , ,
где суммирование производится по всевозможным разбиениям множества
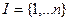
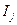 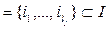 , , 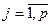 , , 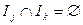 , , 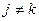 , ,  . .
При 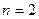
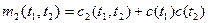 , ,
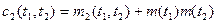 , ,
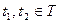 . .
При 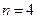
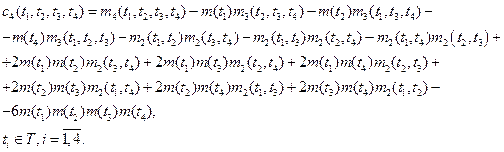
Спектральной плотностью
случайного процесса 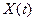 , , 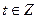 , называется функция вида , называется функция вида
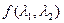 = =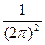 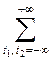 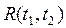 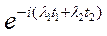 , , 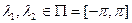 , ,
при условии, что
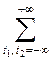 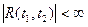
Из определения видно, что спектральная плотность 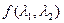 непрерывная, периодическая функция с периодом, равным непрерывная, периодическая функция с периодом, равным 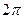 по каждому из аргументов. по каждому из аргументов.
Семиинвариантной спектральной плотностью 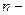 го порядка, го порядка,
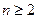 , случайного процесса , случайного процесса 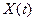 , , 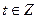 , называется функция вида , называется функция вида
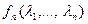 = =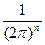 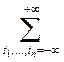 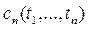 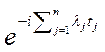 , , 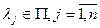 , ,
при условии, что
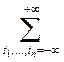 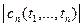 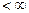 . .
Теорема 1.
Для смешанного семиинварианта 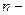 го порядка, го порядка, 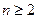 , случайного процесса , случайного процесса 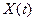 справедливы представления справедливы представления
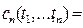 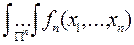 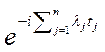 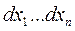 , ,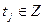 . .
Пусть 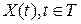 - случайный процесс, заданный на вероятностном пространстве - случайный процесс, заданный на вероятностном пространстве 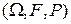 , и , и
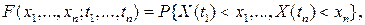
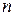 - мерная функция распределения, где - мерная функция распределения, где 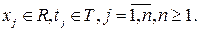
Случайный процесс 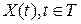 называется стационарным в узком смысле
(строго стационарным), если для любого натурального называется стационарным в узком смысле
(строго стационарным), если для любого натурального 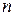 , любых , любых 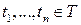 и любого и любого 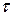 , такого что , такого что 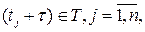 выполняется соотношение выполняется соотношение
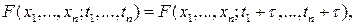
где 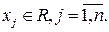
Возьмем произвольное 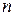 . Пусть . Пусть 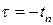 , тогда , тогда
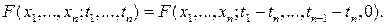
В дальнейшем функцию, в правой части (1), будем обозначать
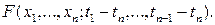
Используя определение стационарного в узком смысле СП 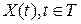 , смешанный момент , смешанный момент 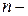 го порядка, го порядка, 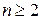 , будем обозначать , будем обозначать
Реклама

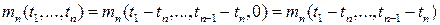 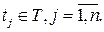
Смешанный семиинвариант 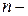 го порядка, го порядка, 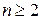 , стационарного в узком смысле СП , стационарного в узком смысле СП 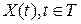 будем обозначать будем обозначать
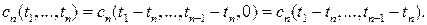 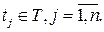
Случайный процесс 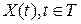 , называется стационарным в широком смысле
, если , называется стационарным в широком смысле
, если 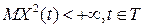 и и
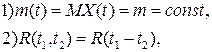
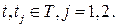
Замечание 1.
Если 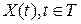 , является стационарным в узком смысле СП и , является стационарным в узком смысле СП и 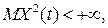 то то 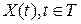 , является стационарным в широком смысле, но не наоборот. , является стационарным в широком смысле, но не наоборот.
Спектральной плотностью
стационарного случайного процесса 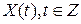 , называется функция вида , называется функция вида
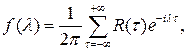 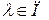 , ,
при условии, что
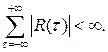
Семиинвариантной спектральной плотностью 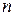 - го порядка
, - го порядка
, 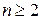 , стационарного СП , стационарного СП 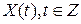 , называется функция вида , называется функция вида
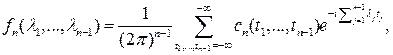
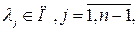
при условии, что
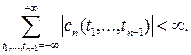
Для смешанного семиинварианта 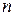 -го порядка, -го порядка, 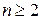 , стационарного СП , стационарного СП 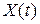 справедливо следующее соотношение справедливо следующее соотношение
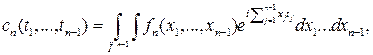 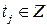 . .
Для 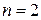 эти соотношения примут вид эти соотношения примут вид
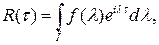 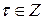 . .
  2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ 2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
Рассмотрим действительный стационарный в широком смысле случайный процесс 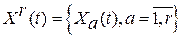 , ,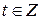 , с математическим ожиданием , с математическим ожиданием 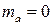 , , 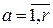 , взаимной ковариационной функцией , взаимной ковариационной функцией 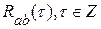 , и взаимной спектральной плотностью , и взаимной спектральной плотностью 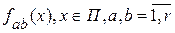 . .
Предположим, имеются Т последовательных, полученных через равные промежутки времени наблюдений  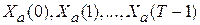 за составляющей за составляющей 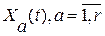 , рассматриваемого процесса , рассматриваемого процесса 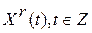 . Как оценку взаимной спектральной плотности в точке . Как оценку взаимной спектральной плотности в точке 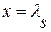 рассмотрим статистику рассмотрим статистику
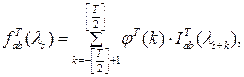 (2.1) (2.1)
где 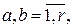 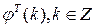 , - произвольная, не зависящая от наблюдений четная целочисленная функция, , - произвольная, не зависящая от наблюдений четная целочисленная функция, 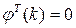 для для 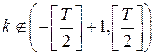 , а , а
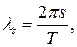 (2.2) (2.2)
s – целое число, 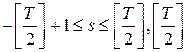 - целая часть числа - целая часть числа 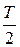 . .
Статистика 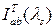 , называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением , называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением
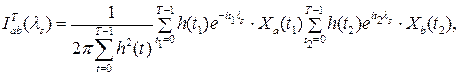 (2.3) (2.3)
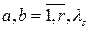 определено равенством (2.2). определено равенством (2.2).
Предположим, если оценка 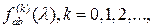 взаимной спектральной плотности взаимной спектральной плотности 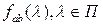 , построенная по T наблюдениям, является асимптотически несмещенной, то математическое ожидание ее можно представить в виде , построенная по T наблюдениям, является асимптотически несмещенной, то математическое ожидание ее можно представить в виде
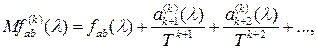 (2.4) (2.4)
где 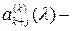 некоторые действительные функции, не зависящие от T, некоторые действительные функции, не зависящие от T, 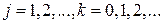
В качестве оценки взаимной спектральной плотности возьмем статистику
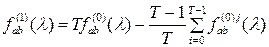 , ,
и исследуем первый момент построенной оценки.
Математическое ожидание построенной оценки будет следующее
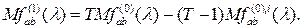
Использовав соотношение (2.4), получим
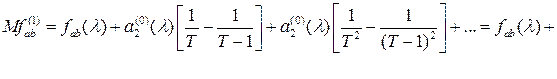 
где
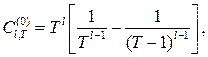 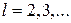
Поскольку
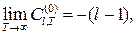
следовательно, оценка 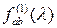 является асимптотически несмещенной со смещением, убывающим как является асимптотически несмещенной со смещением, убывающим как 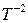 . .
Так как равенство (2.4) справедливо и при 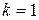 , то, рассматривая оценку , то, рассматривая оценку
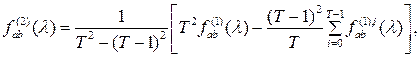
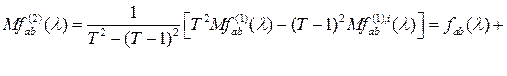
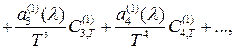
где
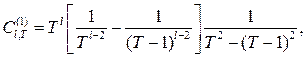
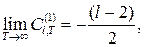
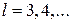 , то оценка , то оценка  является асимптотически несмещенной со смещением, убывающим на является асимптотически несмещенной со смещением, убывающим на 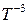 . Далее рассмотрим оценку . Далее рассмотрим оценку
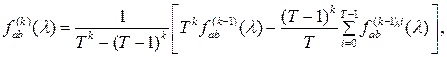 (2.5) (2.5)
Найдем математическое ожидание построенной оценки :
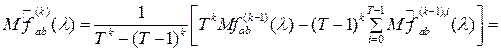
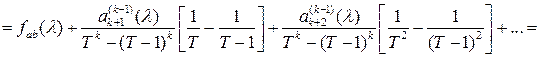
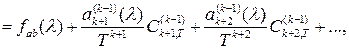
где
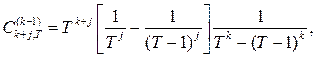
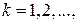 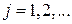
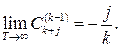
Следовательно, оценка 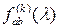 является асимптотически несмещенной со смещением, убывающим как является асимптотически несмещенной со смещением, убывающим как 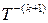 . .
Найдем явный вид коэффициентов 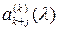 в представлении (2.4), в представлении (2.4), 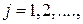 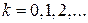
Видим, что
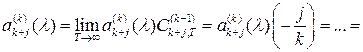
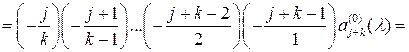 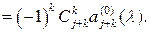
Таким образом, справедливо следующее утверждение.
Теорема 2.1
.
Оценка 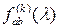 взаимной спектральной плотности взаимной спектральной плотности  стационарного в широком смысле случайного процесса стационарного в широком смысле случайного процесса 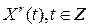 , задаваемая равенством (2.5), удовлетворяет соотношению , задаваемая равенством (2.5), удовлетворяет соотношению
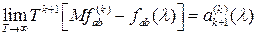 , ,
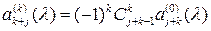 , ,
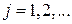 при условии, что справедливо соотношение (2.4) для при условии, что справедливо соотношение (2.4) для 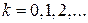
При нахождении моментов оценок спектральных плотностей вторых и высших порядков появляются функции вида
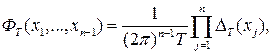 (2.6) (2.6)
где 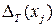 задаются соотношением задаются соотношением 
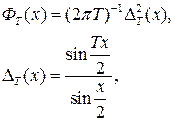
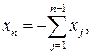 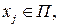 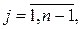 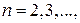 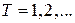
 3. ОКНА ПРОСМОТРА ДАННЫХ 3. ОКНА ПРОСМОТРА ДАННЫХ
Чтобы выделить определенные характеристики спектральных оценок, нередко прибегают к сглаживанию значений на концах случайного временного ряда. Временное сглаживание представляет собой умножение ряда на «окно данных».
В соотношении (2.3) введена функция 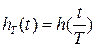 , называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания). , называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания).
Функцию
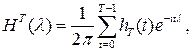 (3.1) (3.1)
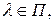 называют частотным окном. Из соотношения (3.1) вытекает, что называют частотным окном. Из соотношения (3.1) вытекает, что
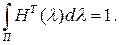
Характерное поведение функции 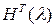 состоит в том, что она становится все более сконцентрированной в окрестности нуля при состоит в том, что она становится все более сконцентрированной в окрестности нуля при 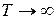 . .
Примеры окон просмотра данных:
1. 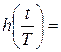 1 – окно Дирихле; 1 – окно Дирихле;
2. 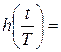 1- 1-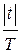 – окно Фейера; – окно Фейера;
3. 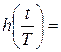 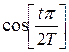 ; ;
4. 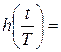 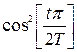 – окно Хэннинга; – окно Хэннинга;
5. 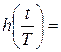 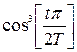 – окно Хэмминга; – окно Хэмминга;
6. 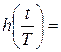 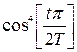 – окно Хэмминга; – окно Хэмминга;
7. 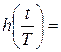 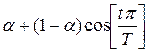 , где , где 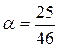 – окно Хэмминга; – окно Хэмминга;
8. 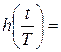 1- 1-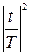 – окно Рисса. – окно Рисса.
 ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
В данной работе исследована оценка спектральной плотности вида
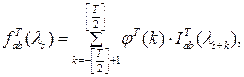
где 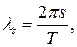 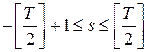 , а периодограмма задана следующим соотношением , а периодограмма задана следующим соотношением
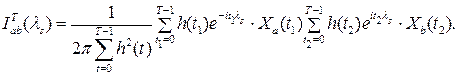
Построены графики этой оценки для различных окон данных на основании данных, представляющих собой последовательность наблюдений - температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
Графики построены также для центрированного случайного процесса.
 СПИСОК
ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
СПИСОК
ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
1. Андерсон Т. Статистический анализ временных рядов. – М.: Мир, 1976. – 755 с.
2. Бриллинджер Д. Временные ряды. Обработка данных и теория. - М.: Мир, 1980. - 536 с.
3. Журбенко И.Г. Спектральный анализ временных рядов. - М.: Изд-во МГУ, 1982. - 168 с.
4. Труш Н.Н. Асимптотические методы статистического анализа временных рядов. – Мн.: БГУ, 1999. - 218 с.
5. Труш Н.Н., Мирская Е.И. Случайные процессы. Преобразования Фурье наблюдений. – Мн.: БГУ, 2000.
ПРИЛОЖЕНИЕ
Для исследования оценки (3.1) был исследован ряд, состоящий из 176 наблюдений ежедневной температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
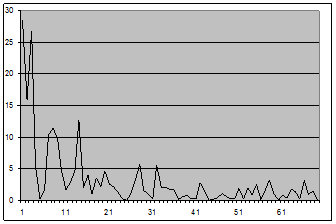
Рис. 1 - График оценки спектральной плотности (2.1) для окна Дирихле
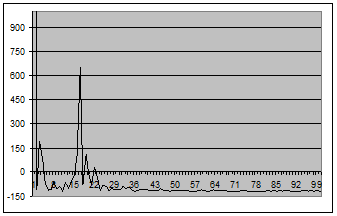
Рис. 2 - График оценки спектральной плотности (2.1) для окна Дирихле для центрированного случайного процесса
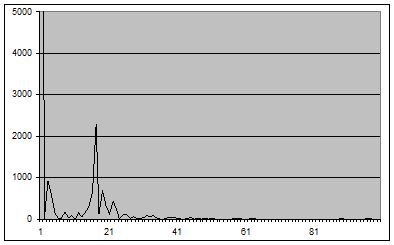
Рис. 3 - График оценки спектральной плотности (2.1) для окна Фейера
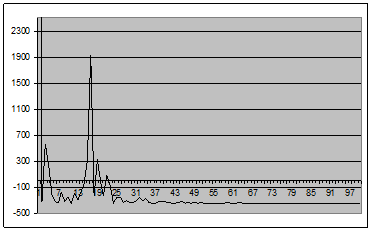
Рис. 4 - График оценки спектральной плотности (2.1) для окна Фейера для центрированного случайного процесса
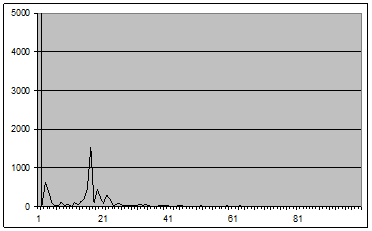
Рис. 5 - График оценки спектральной плотности (2.1) для окна вида 3
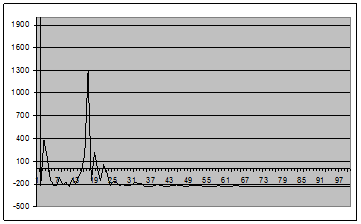
Рис. 6 - График оценки спектральной плотности (2.1) для окна вида 3 для центрированного случайного процесса
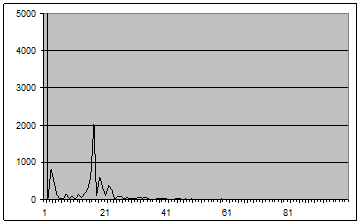
Рис. 7 - График оценки спектральной плотности (2.1) для окна Хэннинга
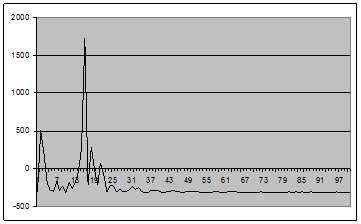
Рис. 8 - График оценки спектральной плотности (2.1) для окна Хэннинга для центрированного случайного процесса
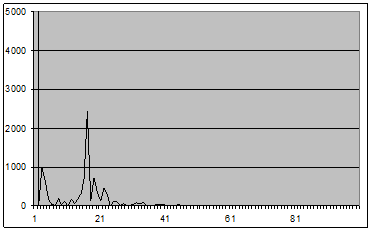
Рис. 9 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 5
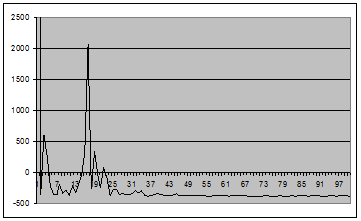
Рис. 10 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 5 для центрированного случайного процесса
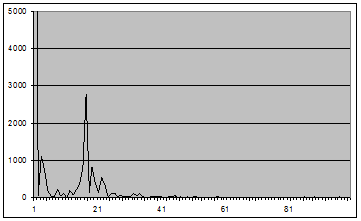
Рис. 11 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 6
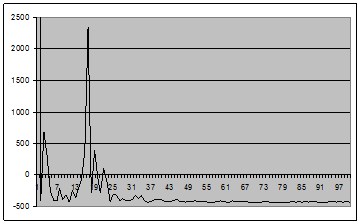
Рис. 12 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 6 для центрированного случайного процесса
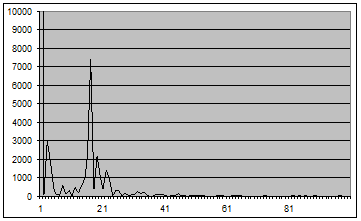
Рис. 13 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 7
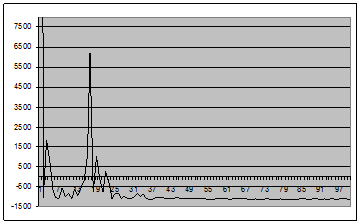
Рис. 14 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 7 для центрированного случайного процесса
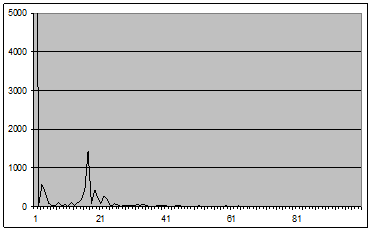
Рис. 15 - График оценки спектральной плотности (2.1) для окна Рисса
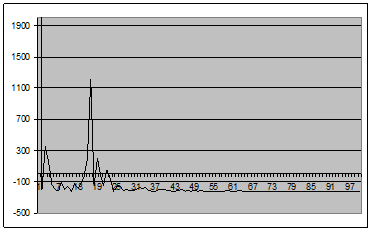
Рис. 16 - График оценки спектральной плотности (2.1) для окна Рисса для центрированного случайного процесса
|