МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО - ЭКОНОМИЧЕСКАЯ
АКАДЕМИЯ
Кафедра А и ИТ
Курсовая работа
по дисциплине «Программирование и основы алгоритмизации»
Вариант № 22
Выполнил: студент
группы № 4241-с
Валиев М.Р.
Проверил: доцент
Савицкий С.К.
Набережные Челны
2011
Задание
1. Найти минимум функции tg(0.55x+0.1)–x2
методом золотого сечения.
1.1 Выбрать начальный отрезок, содержащий минимум функции. Для этого построить график функции. При построении графиков функции следует предварительно выбрать расположение координатных осей и масштаб на них.
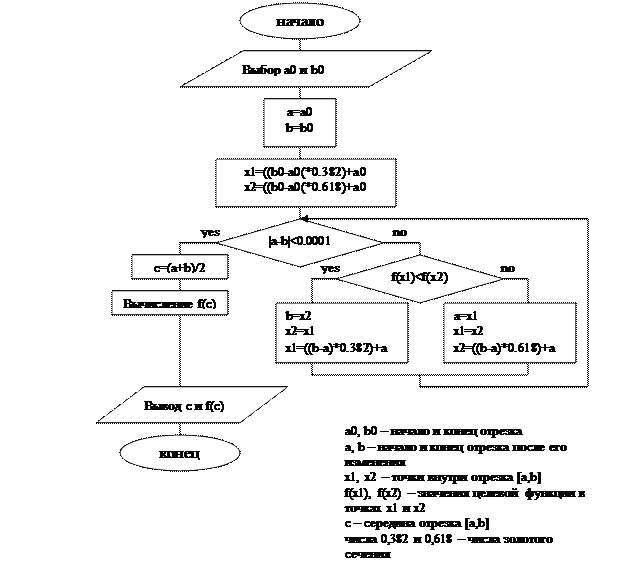
1.2 Составить блок-схему алгоритма.
1.3 Отладить и выполнить программу на ЭВМ, получить с заданной точностью е=10-4
максимум функции.
1.4 Для контроля подставить найденный корень в уравнение и сравнить результат с «е» (он должен быть меньше «е»).
1.5 Проверить полученное решение путем построения графиков в Excel или MathCAD.
2. Дана целочисленная матрица a[ij] i, j=1, ..., n. Получить b1
, ..., bn
, где bi
– это maxaij
1 £ j £n.
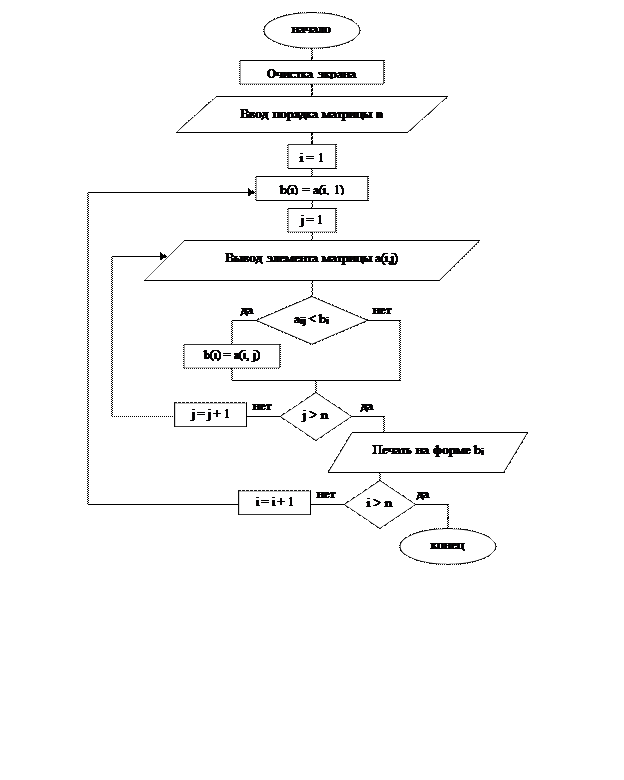
2.1 Составить блок-схему алгоритма.
2.2 Отладить и выполнить программу на ЭВМ.
Теоретическое обоснование методов решения
Задание 1
Метод золотого сечения. Этот метод является одним из наиболее эффективных методов, в котором при ограниченном количестве вычислений целевой функции f(x) достигается наилучшая точность. Суть метода заклюю чается в построении последовательности отрезков [a0
,b0
], [a1
,b1
], … стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) производится лишь один раз. Эта точка, называемая золотым сечением, выбирается так, чтобы отношение длинны большого отрезка к длине всего отрезка равнялось отношению длинны меньшего отрезка к длине большого отрезка lб
/l=lм
/lб
. Поскольку неизвестно в какой последовательности (lм
и lб
или lм
и lб
) делить интервал неопределенности, то рассматривают внутренние точки, соответствующие двум способам деления.
На первом шаге процесса оптимизации внутри отрезка [a0
,b0
] выбираются две внутренние точки х1
и х2
и вычисляются значения целевой функции f(x1
) f(x2
). Поскольку в данном случае f(x1
) < f(x2
) , очевидно, что минимум расположен на одном из прилегающих к x1
отрезков [a1
x1
] или [x1
x2
]. Поэтому отрезок [x2
b0
] можно отбросить, сузив тем самым первоначальный интервал неопределенности.
Реклама

Второй шаг проводим на отрезке [a1
,b1
], где a1
=a0
b1
=x2
. Нужно снова выбрать две внутренние точки, но одна из них х1
осталась из предыдущего шага x3
=x1
, поэтому достаточно выбрать лишь одну точку x4
, вычислить значение f(x4
) и провести сравнение. Поскольку f(x4
) < f(x3
) , ясно что минимум находится на отрезке [х4
,b1
]. Обозначим этот отрезок [a2
,b2
], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длинна очередного отрезка [an
,bn
] не станет меньше заданной величины е
Задание 2
Массив
- это регулярная структура данных одного типа, где все компоненты могут выбираться произвольно и являются одинаково доступными. Регулярность заключается в том, что все данные организованы по одной закономерности. Для обеспечения доступа к любому элементу массива вводится специальное число называемое индексом.
Индекс
- это целое число или совокупность целых чисел, указывающих местоположение элемента в массиве.
Массивы применяются в широкой области приложений, например:
1. Векторы. Управляющие воздействия, которые изменяют состояние системы, обычно задаются в виде векторов, называемых управляющими векторами.
2. Матрицы. Системы управления часто описывают в виде систем дифференциальных уравнений, для решения которых применяют представление данных в виде систем матриц.
3. Тензоры. Для графических данных на экране дисплея помимо двухмерного массива, отображающего место символа или элемента, существует еще и третья координата - цветовая гамма.
Листинг программ
Текст программы 1:
Dim a As Double, b As Double 'отрезок
Dim m 'масштаб
Dim i 'счетчик
DimX 'координата х
DimY 'значение f(x)
Dimu 'смещение по Оу
Dimw 'смещение по оси Ох
Private Sub Command1_Click()
Cls 'очистка экрана
a = -5
b = 5
Calldraw 'вызов функции, которая рисует график
EndSub
PublicSubdraw() 'функция, рисующая график
'разметка по Ох (правая часть)
For i = 0 To b + 1
Line (w + i * m, u - 0.1)-(w + i * m, u + 0.1)
Printi;
Nexti
'разметка по Ох (левая часть)
For i = 0 To a - 1 Step -1
Line (w + i * m, u - 0.1)-(w + i * m, u + 0.1)
Реклама

Printi;
Nexti
'разметка по Оу (верхняя часть)
For i = 1 To 20
Line (w - 0.1, u - i * m)-(w + 0.1, u - i * m)
Printi
Nexti
'разметка по Оу (нижняя часть)
For i = 1 To 4
Line (w - 0.1, u + i * m)-(w + 0.1, u + i * m)
Print "-"; i
Nexti
'рисование графика по точкам
For X = a To b Step 0.0001
Y = -(Tan(0.55 * X + 0.1) - X ^ 2)
PSet (X * m - a * m + 0 + m * a + w, Y * m + u)
Next
'рисование осей Ох и Оу
Line (0, u)-(30, u)
Line (w, 0)-(w, 30)
End Sub
Private Sub Form_Load()
m = 1.5 'начальный масштаб
u = 3 'начальное смещение координат относительно Оy
w = 4 'начальное смещение координат относительно Оx
EndSub
'вычисление минимума методом сечения
Private Sub Command4_Click()
Dim a, b, x1, x2, fx1, fx2
Dim c As Currency
Dim f_c As Currency
Dim a0, b0, e
a0 = Val(InputBox("a"))
b0 = Val(InputBox("b"))
a = a0
b = b0
x1 = ((b0 - a0) * 0.382) + a0
x2 = ((b0 - a0) * 0.618) + a0
Do Until Abs(b - a) < 0.0001
If (Tan(0.55 * x1 + 0.1) - x1 ^ 2) < (Tan(0.55 * x2 + 0.1) - x2 ^ 2) Then
b = x2
x2 = x1
x1 = ((b - a) * 0.382) + a
Else
a = x1
x1 = x2
x2 = ((b - a) * 0.618) + a
End If
Loop
c = (a + b) / 2
f_c = Tan(0.55 * c + 0.1) - c ^ 2
Text4.Text = c
Text3.Text = f_c
Calldraw 'вызов функции, которая рисует график
EndSub
Текст программы 2:
Private Sub Command1_Click()
Cls ' очистка экрана
n = InputBox("Введите порядок матрицы")
ReDima(n, n) AsDouble 'переопределение размера массива
ReDimb(n) AsDouble
'ввод элементов матрицы
For i = 1 To n
b(i) = a(i, 1)
For j = 1 To n
a(i, j) = InputBox("Введите пожалуста элемент матрицы: (" + Str(i) + "," + Str(j) + "):")
If a(i, j) > b(i) Then b(i) = a(i, j)
Next j
Print b(i)
Next i
End Sub
Private Sub zad_Click()
MsgBox ("Дана целочисленная матрица a[ij] i, j=1, ..., n. Получить b[1], ..., b[n], где b[i] - это max a[ij]= 1<= j<= n.")
End Sub
Скриншоты программ
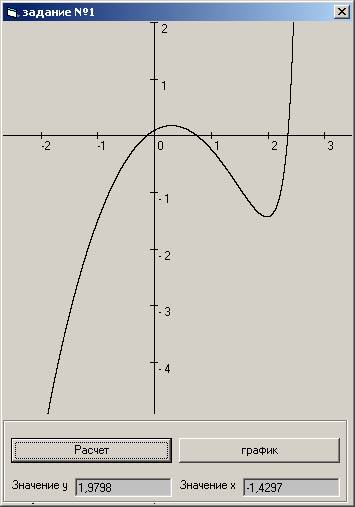
Блок-схемы алгоритмов решения
Метод золотого сечения (1 задание)
2 задание
Проверка графика в
MathCAD
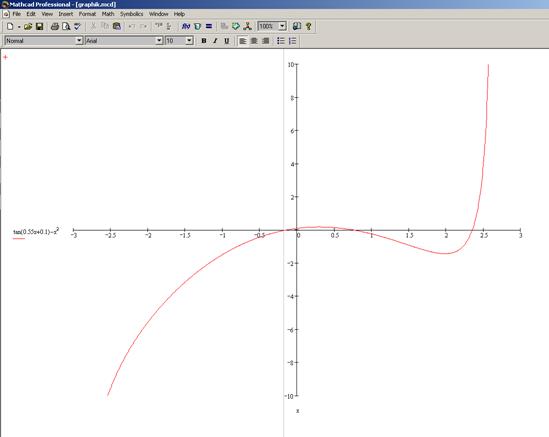
Вывод:
Я научился пользоваться средствами программирования VisualBasicдля нахождения экстремума функции методом золотого сечения и для получения матрицы из нулей и единиц по исходной матрице и по заданному условию
Список использованной литературы
1. Волченков Н. Г. Программирование на VisualBasic 6: Учебное пособие Ч.1 - Ч.3 - М.: ИНФРА-М, 2000.
2. VisualBasic 6.0: Пер. с англ. - СПб.: БХВ-Петербург, 2004. - 992 с.: ил. ISBN 5-8206-0019-3
3. Иванов М.Н., Суворов С.В. Информатика Часть 2. Программирование. Учебно-методическое пособие - М.; МГИУ, 2004
4. Слепцова Л.Д. Программирование на языке VBA. Самоучитель,: -М.: Издательский дом «Вильямс», 2004
5. Браун С. VisualBasic 5 c самого начала - СПб : Питер, 1998
|