Введение
Одной из основных задач теории автоматического регулирования является изучение динамических процессов, происходящих в автоматических системах. Автоматические системы при нормальной эксплуатации должны поддерживать определенный режим работы объекта регулирования при действии на него многих возмущающих факторов. Такое поведение может быть достигнуто лишь в системах автоматического регулирования, обладающих устойчивостью по отношению к этим воздействиям. Устойчивость системы означает, что малое изменение входного сигнала или какого-нибудь возмущения, начальных условий или параметров не приведут к значительным отконениям выходного сигнала. Это определение раскрывает физический смысл понятия устойчивости.
Теория устойчивости, основоположниками которой являются великий русский ученый А.М. Ляпунов и великий французский ученый А.Пуанкаре, представляет собой важный раздел прикладной математики. Создателями современной теории устойчивости являются русские ученые Н.Г. Четаев, Е.А. Барбашин, Н.П. Еругин, Н.Н. Красовский.
1. Понятие устойчивости, асимптотической устойчивости и неустойчивости по Ляпунову.
Рассмотрим задачу Коши для нормальной системы дифференциальных уравнений
(1)
с начальными условиями x ( t0
) = x0
(2)
 где x = ( x1
, x2
, ... , xn
) - n - мерный вектор; t Î I = [t0
, + ¥
[ - независимая переменная, по которой производится дифференцирование; где x = ( x1
, x2
, ... , xn
) - n - мерный вектор; t Î I = [t0
, + ¥
[ - независимая переменная, по которой производится дифференцирование;
f ( t, x ) = ( f1
( t , x ) , f2
( t , x ) , ... , fn
( t , x ) ) - n - мерная вектор - функция.
Комментарии к задаче Коши (1), (2).
Для простоты восприятия эту задачу можно сначала трактовать как задачу Коши для скалярного дифференциального уравнения первого порядка вида x’= f ( t , x ) с начальным условием x ( t0
) = x0
. С целью упрощения все рисунки п. 10
,если нет специальных оговорок, приводится для случая n = 1.
 
x
0 t
Рис.1
|
 Так как задача теории устойчивости впервые возникла в механике, то переменную t принято интерпретировать как время, а искомую вектор-функцию x ( t ) - как движение точки в зависимости от времени в пространстве Rn+1
(рис.1) Так как задача теории устойчивости впервые возникла в механике, то переменную t принято интерпретировать как время, а искомую вектор-функцию x ( t ) - как движение точки в зависимости от времени в пространстве Rn+1
(рис.1)
 Пусть задача Коши (1), (2) удовлетворяет условиям теоремы существования и единственности. Тогда через каждую точку ( t0
, x0
) области единственности решений проходит только одна интегральная кривая. Если начальные Пусть задача Коши (1), (2) удовлетворяет условиям теоремы существования и единственности. Тогда через каждую точку ( t0
, x0
) области единственности решений проходит только одна интегральная кривая. Если начальные  данные ( t0
, x0
) изменяются, то изменяется и решение. Тот факт, что решение зависит от начальных данных, обозначается следующим данные ( t0
, x0
) изменяются, то изменяется и решение. Тот факт, что решение зависит от начальных данных, обозначается следующим    образом: x ( t ) = образом: x ( t ) =  x ( t ; t0
, x0
). Изменение этого решения в данной x ( t ; t0
, x0
). Изменение этого решения в данной  математической модели с изменением начальных данных ( t0
, x0
) математической модели с изменением начальных данных ( t0
, x0
)   приводят к существенному изменению решения x ( t ; t0
, x0
) , приводит к тому, что такой моделью нельзя пользоваться, поскольку приводят к существенному изменению решения x ( t ; t0
, x0
) , приводит к тому, что такой моделью нельзя пользоваться, поскольку  начальные данные ( t0
, x0
) получаются из опыта, а изменения не могут быть абсолютно точными. Естественно, что в качестве математической модели пригодна лишь та задача Коши, которая устойчива к малым изменениям начальных данных. начальные данные ( t0
, x0
) получаются из опыта, а изменения не могут быть абсолютно точными. Естественно, что в качестве математической модели пригодна лишь та задача Коши, которая устойчива к малым изменениям начальных данных.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
    Определим понятие устойчивости, асимптотической устойчивости и неустойчивости в смысле Ляпунова. Для этого отклоение решения x ( t ) = Определим понятие устойчивости, асимптотической устойчивости и неустойчивости в смысле Ляпунова. Для этого отклоение решения x ( t ) =  x ( t ; t0
, x0
) , вызванное отклонением D x0
начального значения x0
, будем записывать следующим образом: x ( t ; t0
, x0
) , вызванное отклонением D x0
начального значения x0
, будем записывать следующим образом:
         | x ( t ; t0
, x0
+ D x0
) - x ( t ) | = | x ( t ; t0
, x0
+ D x0
) - x ( t ; t0
, x0
) |. | x ( t ; t0
, x0
+ D x0
) - x ( t ) | = | x ( t ; t0
, x0
+ D x0
) - x ( t ; t0
, x0
) |.
        Определение 1.
Решение x ( t ) = Определение 1.
Решение x ( t ) =  x ( t ; t0
, x0
) системы (1) называется устойчивым по Ляпунову в положительном направлении (или устойчивым), если оно непрерывно по x0
на интервале I = = [ t0
, + ¥
[ , т.е. "e > 0 $d > 0 такое, что "D x0 x ( t ; t0
, x0
) системы (1) называется устойчивым по Ляпунову в положительном направлении (или устойчивым), если оно непрерывно по x0
на интервале I = = [ t0
, + ¥
[ , т.е. "e > 0 $d > 0 такое, что "D x0
 | D x0
| £dÞ | x ( t ; t0
, x0
+ D x0
) - x ( t ) | £e" t ³ t0
. | D x0
| £dÞ | x ( t ; t0
, x0
+ D x0
) - x ( t ) | £e" t ³ t0
.
Если, кроме того, отклонение решения x ( t ) стремится к нулю при t ® + ¥
для достаточно малых D x0
, т.е. $D > 0 "D x0
.
      | D x0
| £DÞ | x ( t ; t0
, x0
+ D x0
) - x ( t ) | ® 0 , t ® + ¥
. (3) | D x0
| £DÞ | x ( t ; t0
, x0
+ D x0
) - x ( t ) | ® 0 , t ® + ¥
. (3)
 то решение x ( t ) системы (1) называется асимптотически устойчивым в положительном направлении (или асимптотически устойчивым). то решение x ( t ) системы (1) называется асимптотически устойчивым в положительном направлении (или асимптотически устойчивым).
Аналогично определяются различные типы устойчивости решения в отрицательном направлении.
     Комментарий к определению 1.
1) Геометрически устойчивость по Ляпунову решение х ( t ) можно интерпритировать следующим образом ( рис.1 ) : все решения x ( t ; t0
, x0
+ D x0
) , близкие в начальный момент t0
к решению x ( t ) (т.е. начинающиеся в пределах d - трубки ) , не выходят за пределы e - трубки при всех значениях t ³ t0
. Комментарий к определению 1.
1) Геометрически устойчивость по Ляпунову решение х ( t ) можно интерпритировать следующим образом ( рис.1 ) : все решения x ( t ; t0
, x0
+ D x0
) , близкие в начальный момент t0
к решению x ( t ) (т.е. начинающиеся в пределах d - трубки ) , не выходят за пределы e - трубки при всех значениях t ³ t0
.
 
x
0 t
Рис.2
|
     2) Асимптотическая устойчивость есть устойчивость с дополнительным условием (3) : любое решение x1
( t ) , начинающееся в момент t0
в D - трубке, с течением времени неограниченно приближается к решению x ( t ) (рис.2). Трубка радиуса D называется областью притяжения решения x ( t ). Решение x2
( t ), начинающееся при t = t0
за пределами области притяжения, но в пределах d - трубки, не покидает e - трубку, хотя может и не приближаться к решению x(t). 2) Асимптотическая устойчивость есть устойчивость с дополнительным условием (3) : любое решение x1
( t ) , начинающееся в момент t0
в D - трубке, с течением времени неограниченно приближается к решению x ( t ) (рис.2). Трубка радиуса D называется областью притяжения решения x ( t ). Решение x2
( t ), начинающееся при t = t0
за пределами области притяжения, но в пределах d - трубки, не покидает e - трубку, хотя может и не приближаться к решению x(t).
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
  Определение 2.
Решение x ( t ) = x ( t ; t0
, x0
) системы (1) называется неустойчивып по Ляпунову в положительном направлении (или неустойчивым), если оно не является устойчивым в положительном направлении. Определение 2.
Решение x ( t ) = x ( t ; t0
, x0
) системы (1) называется неустойчивып по Ляпунову в положительном направлении (или неустойчивым), если оно не является устойчивым в положительном направлении.
Аналогично определяется неустойчивость в отрицательном направлении.
 Комментарий к определению 2.
Геометрически неустойчивость по Ляпунову означает, что среди решений, близких в начальный момент t0
к решению х ( t ) , найдется хотя бы одно, которое в некоторый момент t1
( свой для каждого такого решения) выйдет за пределы e - трубки (рис.3). Комментарий к определению 2.
Геометрически неустойчивость по Ляпунову означает, что среди решений, близких в начальный момент t0
к решению х ( t ) , найдется хотя бы одно, которое в некоторый момент t1
( свой для каждого такого решения) выйдет за пределы e - трубки (рис.3).
Приведем примеры из механики, иллюстрирующие определения различных типов устойчивости для одномерного случая, т.е. n = 1.
Рассмотрим маятник, состоящий из точечной массы m, укрепленной на невесомом стержне длиной l (рис.4). Выведем маятник из состояния I, отклонив стержень на угол a ; тогда, как известно из опыта, он будет стремиться занять вновь положение I. Если пренебречь сопротивлением окружающей среды, то маятник будет колебаться возле положения I сколь угодно долго с амплитудой, равной начальному отклонению, - это модель устойчивого положения равновесия. Если же учитывать сопротивление окружающей среды, то амплитуда колебаний маятника будет уменьшаться и в итоге он снова займет положение I - это модель асимптотически устойчивого положения равновесия. Если маятник находится в положении II, то малейшее его смещение приведет к удалению маятника от состояния II - это модель не устойчивого положения равновесия.
 
x
0 t
Рис.3 Рис.4
      Исследование устойчивости произвольного решения x ( t ) системы (1) всегда можно свести к исследованию устойчивости нулевого решения некоторой преобразованной системы. Действительно, в системе (1) произведем подстановку y ( t ) = x - x (t). Тогда получим систему Исследование устойчивости произвольного решения x ( t ) системы (1) всегда можно свести к исследованию устойчивости нулевого решения некоторой преобразованной системы. Действительно, в системе (1) произведем подстановку y ( t ) = x - x (t). Тогда получим систему
 y’ = F ( t, y ). (4) y’ = F ( t, y ). (4)
          где F ( t , y ) = f ( t , y ( t ) + x ( t ) ) - f ( t , x ( t ) ) , F (t, 0) º 0 " t ³ t0
. где F ( t , y ) = f ( t , y ( t ) + x ( t ) ) - f ( t , x ( t ) ) , F (t, 0) º 0 " t ³ t0
.
   Решению x ( t ) системы (1) соответствует нулевое решение y (t) º 0 системы (4). Решению x ( t ) системы (1) соответствует нулевое решение y (t) º 0 системы (4).
     В дальнейшем будем предполагать, что система (1) имеет нулевое решение, т.е. f ( t , 0 ) = 0 " t ³ t0
, и ограгничимся исследованием устойчивости нулевого решения. Переформулируем определения различных типов устойчивости для нулевого решения x ( t ) º 0 системы (1). В дальнейшем будем предполагать, что система (1) имеет нулевое решение, т.е. f ( t , 0 ) = 0 " t ³ t0
, и ограгничимся исследованием устойчивости нулевого решения. Переформулируем определения различных типов устойчивости для нулевого решения x ( t ) º 0 системы (1).
  Определение 3.
Нулевое решение x ( t ) º 0 системы (1) называется устойчивым по Ляпунову в положительном направлении (или устойчивым), если "e > 0 $d = d ( e ) > 0 такое, что " x0 Определение 3.
Нулевое решение x ( t ) º 0 системы (1) называется устойчивым по Ляпунову в положительном направлении (или устойчивым), если "e > 0 $d = d ( e ) > 0 такое, что " x0
| D x0
| £dÞ | x ( t ; t0
, x0
) | £e" t ³ t0
.
Если кроме того,
    $ $ D > 0 " x0
| D x0
| £DÞ | x ( t ; t0
, x0
) | ® 0 , t ® + ¥
, D > 0 " x0
| D x0
| £DÞ | x ( t ; t0
, x0
) | ® 0 , t ® + ¥
,
  то решение x ( t ) º 0 системы (1) называется асимптотически устойчивым в положительном направлении ( или асимптотически устойчивым ) . то решение x ( t ) º 0 системы (1) называется асимптотически устойчивым в положительном направлении ( или асимптотически устойчивым ) .
    Определение 4.
Нулевое решение x ( t ) º 0 системы (1) называется неустойчивым по Ляпунову в положительном направлении (или неустойчиво), если оно не является устойчивым в положительном направлении, т.е. Определение 4.
Нулевое решение x ( t ) º 0 системы (1) называется неустойчивым по Ляпунову в положительном направлении (или неустойчиво), если оно не является устойчивым в положительном направлении, т.е.
  $e > 0 $ t1
> t0
"d > 0 x0
¹ 0 | x0
| £dÞ | x ( t ; t0
, x0
) | > e . $e > 0 $ t1
> t0
"d > 0 x0
¹ 0 | x0
| £dÞ | x ( t ; t0
, x0
) | > e .
Геометрическая интерпритация устойчивости, асимптотической устойчивости и неустойчивости нулевого решения x ( t ) º 0 системы (1) дана соответственно на рис.5-7.
  x x
t
0
Рис.5
|
  x x
t
0
Рис.6
|
  x x
t
0
Рис.7
|
2. Устойчивость решения автономной системы. Устойчивость решения системы линейных дифференциальных уравнений с постоянными коэффициентами.
Система обыкновенных дифференциальных уравнений называется автономной (или стационарной, или консервативной, или динамической), если независимая переменная не входит явно в систему уравнений.
Нормальную автономную систему n - го порядка можно записать в векторной форме :
   dx / dt = f ( x ). (5) dx / dt = f ( x ). (5)
Рассмотрим задачу Коши для системы (5) с начальными условиями (2). В дальнейшем предполагаем, что задача Коши (5), (2) удовлетворяет условиям теоремы существования и единственности.
    Пусть x = x ( t ) - есть решение системы (5). Направленная кривая g , которую можно параметрически задать в виде xi
= xi
( t ) ( i = 1, ... , n ), называется траекторией (фазовым графиком) системы (5) или траекторией решения x = x ( t ). Пространство Rn
с координатами ( x1
, ... , xn
), в котором расположены траектории системы (5), называется фазовым пространством автономной системы (5). Известно, что интегральные кривые системы (5) можно параметрически задать в виде t = t , x1
= x1
( t ), ... , xn
= xn
( t ). Следовательно, интегральная кривая принадлежит пространству Rn+1
с координатами ( t , x1
, x2
, ... , xn
) , а траектория является проекцией интегральной кривой на пространство Rn
параллельно оси t. Проиллюстрируем это для случая n = 2 , т.е. когда Rn+1
- трехмерное пространство, а фазовое пространство Rn
- двумерная плоскость. На рис.8,а изображена интегральная кривая, заданная параметрическими уравнениями t = t, x1
= x1
( t ) , x2
= x2
( t ), на рис.8,б - ее проекция на плоскость, т.е. траектория, заданная параметрическими уравнениями x1
= x1
( t ) , x2
= x2
( t ). Стрелкой указано направление возрастания параметра t. Пусть x = x ( t ) - есть решение системы (5). Направленная кривая g , которую можно параметрически задать в виде xi
= xi
( t ) ( i = 1, ... , n ), называется траекторией (фазовым графиком) системы (5) или траекторией решения x = x ( t ). Пространство Rn
с координатами ( x1
, ... , xn
), в котором расположены траектории системы (5), называется фазовым пространством автономной системы (5). Известно, что интегральные кривые системы (5) можно параметрически задать в виде t = t , x1
= x1
( t ), ... , xn
= xn
( t ). Следовательно, интегральная кривая принадлежит пространству Rn+1
с координатами ( t , x1
, x2
, ... , xn
) , а траектория является проекцией интегральной кривой на пространство Rn
параллельно оси t. Проиллюстрируем это для случая n = 2 , т.е. когда Rn+1
- трехмерное пространство, а фазовое пространство Rn
- двумерная плоскость. На рис.8,а изображена интегральная кривая, заданная параметрическими уравнениями t = t, x1
= x1
( t ) , x2
= x2
( t ), на рис.8,б - ее проекция на плоскость, т.е. траектория, заданная параметрическими уравнениями x1
= x1
( t ) , x2
= x2
( t ). Стрелкой указано направление возрастания параметра t.
x2
x2
0 t 0 x1
x1
а) Рис.8 б)
|
     Определение 5.
Точка ( a1
, a2
, ... , an
) называется точкой покоя (положением равновесия) автономной системы (5), если правые части f1
, f2
, ... , fn
системы (5) обращаются в этой точке в нуль, т.е. f (a) = 0,где a = ( a1
, a2
, ... , an
) , 0 = ( 0 , 0 , ... , 0 ) . Определение 5.
Точка ( a1
, a2
, ... , an
) называется точкой покоя (положением равновесия) автономной системы (5), если правые части f1
, f2
, ... , fn
системы (5) обращаются в этой точке в нуль, т.е. f (a) = 0,где a = ( a1
, a2
, ... , an
) , 0 = ( 0 , 0 , ... , 0 ) .
       Если ( a1
, ... , an
) - точка покоя, то система (5) имеет постоянное решение x ( t ) = a. Как известно, исследование устойчивости любого, а значит, и постоянного решения a можно свести к исследованию устойчивости нулевого решения. Поэтому далее будем считать, что система (5) имеет нулевое решение x ( t ) º 0 , т.е. f ( 0 ) = 0, и точка покоя совпадает с началом координат фазового пространства Rn
. В пространстве Rn+1
точке покоя соответствует нулевое решение. Это изображено на рис.8 для случая n = 2. Если ( a1
, ... , an
) - точка покоя, то система (5) имеет постоянное решение x ( t ) = a. Как известно, исследование устойчивости любого, а значит, и постоянного решения a можно свести к исследованию устойчивости нулевого решения. Поэтому далее будем считать, что система (5) имеет нулевое решение x ( t ) º 0 , т.е. f ( 0 ) = 0, и точка покоя совпадает с началом координат фазового пространства Rn
. В пространстве Rn+1
точке покоя соответствует нулевое решение. Это изображено на рис.8 для случая n = 2.
Таким образом, устойчивость нулевого решения системы (5) означает устойчивость начала координат фазового пространства системы (5), и наоборот.
  Дадим геометрическую интерпретацию устойчивого, асимптотически устойчивого и неустойчивого начала плоскости, т.е. когда n = 2. Для этого следует спроектировать аналоги рис.5-7 в двумерном случае на фазовую плоскость R2
, причем проекциями e - трубки и d - трубки являются окружности с радиусами e и d . Начало x = 0 устойчиво, если все траектории, начинающиеся в пределах d - окружности, не покидают e - окружность " t ³ t0
(рис.9) ; асимптотически устойчиво, если оно устойчиво и все траектории, начинающиеся в области притяжения D , стремятся к началу (рис.10) ; неустойчиво, если для любой e - окружности и всех d > 0 существует хотя бы одна траектория, покидающая ее (рис.11). Дадим геометрическую интерпретацию устойчивого, асимптотически устойчивого и неустойчивого начала плоскости, т.е. когда n = 2. Для этого следует спроектировать аналоги рис.5-7 в двумерном случае на фазовую плоскость R2
, причем проекциями e - трубки и d - трубки являются окружности с радиусами e и d . Начало x = 0 устойчиво, если все траектории, начинающиеся в пределах d - окружности, не покидают e - окружность " t ³ t0
(рис.9) ; асимптотически устойчиво, если оно устойчиво и все траектории, начинающиеся в области притяжения D , стремятся к началу (рис.10) ; неустойчиво, если для любой e - окружности и всех d > 0 существует хотя бы одна траектория, покидающая ее (рис.11).
  Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами, имеющая вид Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами, имеющая вид
dx / dt = A x, (6)
где A - постоянная матрица размера n ´ n , является частным случаем системы (5). Следовательно, для этой системы справедливы все сделанные выше утверждения об автономных системах.
3. Простейшие типы точек покоя.
Пусть имеем систему дифференциальных уравнений
æ dx / dt = P ( x , y ),
í(A)
î dy / dt = Q ( x , y ).
Точка ( x0
, y0
) называется точкой покоя или особой точкой системы (A), если P ( x0
, y0
) = 0 , Q ( x0
, y0
) = 0.
Рассмотрим систему
æ dx / dt = a11
x + a12
y,
í(7)
î dy / dt = a21
x + a22
y.
где aij
( i , j = 1 , 2 ) - постоянные. Точка ( 0 , 0 ) является точкой покоя системы (7). Исследуем расположение траектории системы (7) в окрестности этой точки. Ищем решение в виде
x = a1
e k t
, y = a2
e k t
. (8)
Для определения k получаем характеристическое уравнение
  a11
- k a12 a11
- k a12
= 0. (9)
a21
a22
- k
Рассмотрим возможные случаи.
I. Корни характеристического уравнения действительны и различны.
Подслучаи :
1) k1
< 0, k2
< 0. Точка покоя асимптотически устойчива (устойчивый узел).
2) k1
> 0, k2
> 0. Точка покоя неустойчива (неустойчивый узел).
3) k1
> 0, k2
< 0. Точка покоя неустойчива (седло).
4) k1
= 0, k2
> 0. Точка покоя неустойчива.
5) k1
= 0, k2
< 0. Точка покоя устойчива, но не асимптотически.
II. Корни характеристического уравнения комплексные
: k1
= p + q i, k2
= p - q i. Подслучаи :
1) p < 0 , q ¹ 0. Точка покоя асимптотически устойчива (устойчивый фокус).
2) p > 0 , q ¹ 0. Точка покоя неустойчива (неустойчивый фокус).
3) p = 0, q ¹ 0. Точка покоя устойчива (центр). Асимптотической устойчивости нет.
III. Корни кратные
: k1
= k2
. Подслучаи :
1) k1
= k2
< 0. Точка покоя асимптотически устойчива (устойчивый узел).
2) k1
= k2
> 0. Точка покоя неустойчива (неустойчивый узел).
3) k1
= k2
= 0. Точка покоя неустойчива. Возможен исключительный случай, когда все точки плоскости являются устойчивыми точками покоя.
Для системы линейных однородных уравнений с постоянными коэффициентами
dxi
n
 = å ai j
xj
( i = 1 , 2 , ... , n ) (10) = å ai j
xj
( i = 1 , 2 , ... , n ) (10)
dt i=1
 характеристическим уравнением будет характеристическим уравнением будет
 a11
- k a12
a13
... a1n a11
- k a12
a13
... a1n
a21
a22
- k a23
... a2n
= 0. (11)
. . . . . . . .
an1
an2
an3
... ann
- k
1) Если действительные части всех корней характеристического уравнения (11) системы (10) отрицательны, то точка покоя xi
( t ) º 0 ( i = 1 , 2 , ... , n ) асимптотически устойчива.
2) Если действительная часть хотя бы одного корня характеристического уравнения (11) положительна, Re k i
= p i
> 0, то точка покоя xi
( t ) º 0 ( i = 1, 2, ... n ) системы (10) неустойчива.
3) Если характеристическое уравнение (11) имеет простые корни с нулевой действительной частью (т.е. нулевые или чисто мнимые корни ), то точка покоя xi
( t ) º 0 ( i = 1, 2, ... n ) системы (10) устойчива, но не асимптотически.
Для системы двух линейных линейных уравнений с постоянными действительными коэфициентами
.
æ x = a11
x + a12
y,
í . (12)
î y = a21
x + a22
y
характеристическое уравнение (9) приводится к виду
k2
+ a1
k + a2
= 0.
1) Если a1
> 0 , a2
> 0, то нулевое решение системы (12) асимптотически устойчиво.
2) Если а1
> 0 , a2
= 0, или a1
= 0 , a2
> 0 , то нулевое решение устойчиво, но не асимптотически.
3) Во всех остальных случаях нулевое решение неустойчиво; однако при a1
= a2
= 0 возможен исключительный случай, когда нулевое решение устойчиво, но не асимптотически.
4. Критерий устойчивости Михайлова.
Частотные критерии устойчивости получили наиболее широкое практическое применение, так как, во-первых, они позволяют судить об устойчивости замкнутой системы по более простой передаточной функции системы W ( s ) ; во-вторых, анализ устойчивости можно выполнять и по экспериментально определенным частотным характеристикам; в-третьих, с помощью частотных характеристик можно судить и о качестве переходных процессов в системе.
А.В. Михайлов первым предложил использовать развитые в радиотехнике Найквистом частотные методы для анализа устойчивости линейных систем регулирования. Сформулированным им в 1938 г. критерий устойчивости назвали его именем. Рассмотрим существо этого критерия.
Пусть характеристическое уравнение замкнутой системы имеет вид
D ( l ) = ln
+ a1
ln-1
+ a2
ln-2
+ ... + an
= 0. (13)
Зная его корни l1
, l2
, ... , ln
, характеристический многочлен для уравнения (13) запишем в виде
D ( l ) = ( l - l1
) ( l - l2
) ... ( l - ln
). (14)
Рис.12. Векторное изображение сомно-жителей характерис-тического уравнения замкнутой системы на плоскости :
а - для двух корней l и li
;
б - для четырех корней l1
, l ‘1
, l2
, l ‘2
Графически каждый комплексный корень l можно представить точкой на плоскости. Поэтому, в свою очередь, каждый из сомножителей уравнения (14) можно представить в виде разности двух векторов ( l - li
), как это показано на рис.12,а. Положим теперь, что l = j w ; тогда определяющей является точка w на мнимой оси (рис.12,б). При изменении w от - ¥ до + ¥ векторы j w - l1
и j w - l ‘1
комплексных корней l и l ‘1
повернуться против часовой стрелки, и приращение их аргумента равно + p , а векторы j w - l2
и j w - l ‘2
повернутся по часовой стрелке, и приращение их аргумента равно - p . Таким образом, приращение аргумента arg( j w - li
) для корня характеристического уравнения li
, находящегося в левой полуплоскости, составит + p , а для корня, находящегося в правой полуплоскости, - p . Приращение результирующего аргумента D arg D( j w ) равно сумме приращений аргументов его отдельных сомножителей. Если сре1ди n корней характеристического уравнения m лежит в правой полуплоскости, то приращение аргумента составит
D arg D( j w ) = ( n - m ) p - m p = ( n - 2m ) p . (15)
  -
¥
<
w
<
¥
для левой для правой -
¥
<
w
<
¥
для левой для правой
полуплоскости полуплоскости
Отметим теперь, что действительная часть многочлена
D ( j w ) = ( j w )n
+ a1
( j w )n-1
+ a2
( j w )n-2
+ ... + an
(16)
содержит лишь четные степени w , а мнимая его часть - только нечетные, поэтому
arg D ( j w ) = - arg D ( -j w ), (17)
и можно рассматривать изменение частоты только на интервале w от 0 до ¥ . В этом случае приращение аргумента годографа характеристического многочлена
D arg D( j w ) = ( n - 2m ) p / 2 . (18)
0
£
w
<
¥
Если система устойчива, то параметр m = 0, и из условия (18) следует, что приращение аргумента
D arg D( j w ) = n p / 2 . (19)
0
£
w
<
¥
На основании полученного выражения сформулируем частотный критерий устойчивости Михайлова: для того чтобы замкнутая система автоматического регулирования была устойчива, необходимо и достаточно, чтобы годограф характеристического многочлена в замкнутой системе (годограф Михайлова) начинался на положительной части действительной оси и проходил последовательно в положительном направлении, не попадая в начало координат, n квадрантов комплексной плоскости ( здесь n - порядок характеристического уравнения системы).
 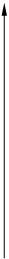  
j V’ j V’
0 U’ 0 U’
а) б)
|
Рис.13. Примеры годографов Михайлова для различных характеристических уравнений замкнутых систем:
а - устойчивые системы при n = 1 - 6 ; б - неустойчивые системы при n = 4 и различных параметрах
Соответствующие устойчивым системам годографы Михайлова для уравнений различных порядков построены на рис. 13,а. На рис. 13,б построены годографы Михайлова для неустойчивых систем при n = 4.
|