1. Векторы. Действия над векторами.
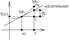
Вектором наз. упорядоченная совокупность чисел Х
={X1
,X2
,...Xn
} вектор дан в n-мерном пространстве. Т(X1
,X2
,X3
). n=1,2,3. Геометрический вектор - направленный отрезок. |AB
|=|a
| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А
||В.
б) l>0, то А
В,
l<0, то А
¯В
. в)l>1, то А
<В
, )l<1, то А
>В
. 2. Разделить вектор на число n значит умножить его на число, обратное n: а
/n=a
*(1/n).
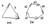 3.Суммой неск-их векторов а
и в
наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а
и в
наз-ся вектор c
, который, будучи сложенным с вектором в
даст вектор а
. 3.Суммой неск-их векторов а
и в
наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а
и в
наз-ся вектор c
, который, будучи сложенным с вектором в
даст вектор а
.
2.3. Декартова прямоугольная система координат. Базис.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
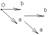 Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов. Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.
 Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве. Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.
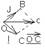 ОС
=OA
+OB, OA
=x*i
, OB
=j*y, OC
=xi
+yj
. Числа х,у наз-ся координатами вектора ОС
в данном базисе ОС
=OA
+OB, OA
=x*i
, OB
=j*y, OC
=xi
+yj
. Числа х,у наз-ся координатами вектора ОС
в данном базисе

4. Действия над векторами.
а
=х1
i
+y1
j
+z1
k
; b
=х2
i
+y2
j
+z2
k
l*a
=l(х1
i
+y1
j
+z1
k
)= l(х1
)i
+l (y1
)j
+l(z1)k
a
±b
=(x1
±x2
)i
+(y1
±y2
)j
+(z1
±z2
)k
ab
=x1
x2
ii
+y1
x2
ij
+x2
z1
ki
+x1
y2
ij
+y1
y2
jj
+ z1
y2
kj
+x1
z1
ik
+y1
z2
jk
+z1
z2
kk
=x1
x2
+y1
y2
+z1
z2
ii
=1; ij
=0; и т.д.
скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.
аа
=x2
+y2
+z2
=|a
|2
a
{x,y,z}, aa
=|a
|*|a
|, то a
2
=|a
|
2
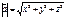
ab
=|a|*|b|*cosj
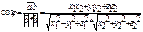
а)ав
=0,<=>а
^в
, x1
x2
+y1
y2
+z1
z2
=0
Реклама

б)а
||в
- коллинеарны, если , x1
/x2
=y1
/y2
=z1
/z2
5. Скалярное произведение векторов и его свойства.
-(“skala”-шкала) 2х векторов а
и в
наз. число, равное произведению длин этих векторов на cos угла между ними. (а
,в
)- скалярное произведение. а
*в
=|а
|*|в
|*cosj, j=p/2, cosp/2=0, a^b=>ab
=0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).
6. Векторное произведение 2х векторов.
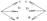
левая ----- правая
Тройка векторов а
,в
,с
наз. правоориентированной (правой), если с конца 3го вектора с
кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а
и в
наз. такой вектор с
, который удовлетворяет условиям: 1. |c
|=|a
|*|b
|*sinj. 2. c
^a
и c
^b
. 3. тройка а
,в
,с
-правая.
7. Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a
*b
*c
=[a
*b
]*c
=a
*[b
*c
], где
a
={ax
,ay
,az
}
b
={bx
,by
,bz
}
c
={cx
,cy
,cz
}
Св-ва:
1. При перестановке 2х сомножителей:
a
*b
*c
=-b
*c
*a
2. не меняется при перестановке циклических сомножителей:
a
*b
*c
=c
*a
*b
=b
*c
*a
3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a
*b
*c
=0
б)если некомпланарные вектора a
,b
,c
привести к 1 началу, то |a
*b
*c
|=Vпараллепипеда, построенного на этих векторах
если a
*b
*c
>0, то тройка a
,b
,c
- правая
если a
*b
*c
<0, то тройка a
,b
,c
- левая
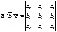
8. Уравнение линии и поверхности.
1. Уравнение сферы. Сфера- геометрическое место точек, равноудаленных от 1ой точки, называемой центром.
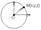 O(a,b,c) O(a,b,c)
|OM
|=r, OM
={x-a,y-b,z-c}
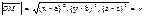
r2
=(x-a)2
+(y-b)2
+(z-c)2
- уравнение сферы. x2
+y2
+z2
=r2
- ур-е сферы с центром точке(0,0).
F(x,y,z)=0- ур-е поверхности - ур-ю, удовлетворяющему координатам x,y,z любой точки, лежащей на поверхности.
2. Уравнение окружности
 |OM
|=r, OM
={x-a,y-b) |OM
|=r, OM
={x-a,y-b)
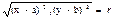
r2
=(x-a)2
+(y-b)2
+(z-c)2
- ур-е окружности
а=b=0, то x2
+y2
=r2
F(x,y)=0- ур-е линии на плоскости.
9. Плоскость в пространстве.
Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.
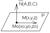 N
-вектор нормали N
-вектор нормали
M
0
M
{x-x0
,y-y0
,z-z0
}
Для того, чтобы точка MÎP, необходимо и достаточно чтобы вектора N
^M
0
M
(т.е. N
*M
0
M
=0)
Реклама

A(x-x0
)+B(y-y0
)+С(z-z0
)=0 - ур-е плоскости, проходящей через данную точку ^вектору.
10. Общее уравнение плоскости.
Ax+By+Сz-Ax0
-By0
-Сz0
=0
-Ax0
-By0
-Сz0
=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
Частный случай:
Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)
Если A=0, то By+Сz+D=0
Если B=0, то Ax +Сz+D=0
Если C=0, то Ax+By+D=0
Если A=B=0, то Сz+D=0
Если A=C=0, то By+D=0
Если A=D=0, то By+Сz=0
Если B=D=0, то Ay+Сz=0
11. Взаимное расположение плоскостей.
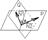
N
1
,N
2
-нормальные векторы плоскости.
P:A1
x+B1
y+C1
z+D1
=0
Q:A2
x+B2
y+C2
z+D2
=0
P^Q{A1
,B1
,C1
}
Q^N
2
{A2
,B2
,C2
}
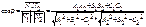
1)Пусть P^Q<=>N1
^N
2
A1
A2
+B1
B2
+C1
C2
=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N
1
^N
2
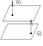
A1
/A2
=B1
/B2
=C1
/C2
- Условие параллельности 2х плоскостей.
A1
/A2
=B1
/B2
=C1
/C2
=D1
/D2
- Условие совпадения 2х плоскостей.
12. Каноническое уравнение прямой в пространстве.
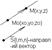
M0
M
{x-x0
,y-y0
,z-z0
}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M
0
M
||S
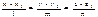
13. Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
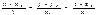

lmn
S
{x2
-x1
,y2
-y1
,z2
-z1
}
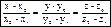
14. прямая, как пересечение плоскостей. Нахождение начальной точки и направляющего вектора прямой.

P:A1
x+B1
y+C1
z+D1
=0
Q:A2
x+B2
y+C2
z+D2
=0
Общее ур-е прямой в пространстве.
Для того, чтобы перейти от общего к каноническому ур-ю прямой, надо задать начальную точку и направляющий вектор:
1. Найдем начальную точку:
Z=0 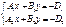
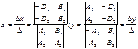
M0
(x0
,y0
,0), т.к. Z=0
2. Найдем направляющий вектор S
-?
P^N1
{A1
,B1
,C1
}
Q^N1
{A2
,B2
,C2
}
S
=N1
*N2
16. Взаимное расположение прямой на плоскости.
P:A1
x+B1
y+C1
z+D1
=0^N1
{A1
,B1
}
Q:A2
x+B2
y+C2
z+D2
=0^N2
{A2
,B2
}
а)
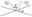
то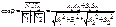
б)
 pq<=> N1
||N2
, то A1
/A2
=B1
/B2 pq<=> N1
||N2
, то A1
/A2
=B1
/B2
в)
 p||q<=> N1
^N2
, то A1
A2
+B1
B2
=0 p||q<=> N1
^N2
, то A1
A2
+B1
B2
=0
 17. Общее ур-е прямой линии на плоскости. Его частные случаи. 17. Общее ур-е прямой линии на плоскости. Его частные случаи.
Сначала запишем ур-е прямой, проходящей через заданную точку ^ заданному вектору.
M0
(x0
,y0
)

M0
M
{x-x0
,y-y0
}
n*M0
M
=0
A(x-x0
)+B(y-y0
)=0
Ax+By-Ax0
-By0
=0
-Ax0
-By0
=C
Ax+By+C=0-общее уравнение прямой на плоскости.
18.19. Каноническое ур-е прямой линии на плоскости. Ур-е прямой, проходящей ч/з 2 точки. Ур-е с угловым коэффициентом.
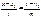
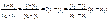 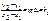
y-y1
=k1
(x-x1
)
y=k1
x-k1
x1
+y1
y1
-k1
x1
=b
y=k1
x+b
ур-е прямой с угловым коэффициентом k.
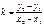  Пусть даны 2 точки M1
(x1
,y1
), M2
(x2
,y2
) и x1
¹x2
, y1
¹y2
. Для составления уравнения прямой М1
М2
запишем уравнения пучка прямых, проходящих через точку М1
: y-y1
=k(x-x1
). Т.к. М2
лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2
в уравнение пучка М1
: y-y1
=k(x-x1
) и найдем k: Пусть даны 2 точки M1
(x1
,y1
), M2
(x2
,y2
) и x1
¹x2
, y1
¹y2
. Для составления уравнения прямой М1
М2
запишем уравнения пучка прямых, проходящих через точку М1
: y-y1
=k(x-x1
). Т.к. М2
лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2
в уравнение пучка М1
: y-y1
=k(x-x1
) и найдем k:
Теперь вид искомой прямой имеет вид:
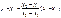 или: или: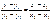
- Ур-е прямой, проходящей ч/з 2
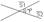 20,21. Угол м/ду прямыми на плоскости. Условия || и
^
. 20,21. Угол м/ду прямыми на плоскости. Условия || и
^
.
а) 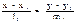
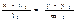
S1
{l1
,m1
} S2
{l2
,m2
},
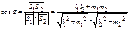
или
p:y=k1
x+b1
, k1
=tgj1
q:y=k2
x+b2
, k2
=tgj2
=>tgj=tg(j2
-j1
)=
=(tgj2
-tgj1
)/(1+ tgj1
tgj2
)=
=(k2
-k1
)/(1+k1
k2
).
б) p||q, tgj=0, k1
=k2
в)p^q,то 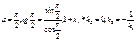
22. Расстояние от точки до прямой на плоскости и до плоскости в пространстве.
1. Ax+By+C=0, M0
(x0
,y0
)
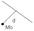
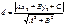
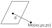
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0
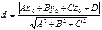
23. Кривые линии 2-го порядка.
Кривые 2го порядка описываются с помощью общего ур-я:
Ax2
+2Bxy+Cy2
+2Dx+2Ey+F=0, где
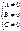
а) Каноническое ур-е эллипса
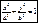 - Каноническое ур-е эллипса - Каноническое ур-е эллипса
Если a=b, то x2
+b2
=a2
- ур-е окружности.
б) Ур-е гиперболы: x2
/a2
-y2
/b2
=1

в) ур-е параболы: y2
=2px или y=ax2
г) ур-е сферы: x2
+y2
+z2
=а2
(r2
=(x-a)2
+(y-b)2
+(z-c)2
)
д) ур-е эллипса: x2
/a2
-y2
/b2
+z2
/c2
=1
24. Парабола и ее свойства.
Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2
, где х и у - текущие координаты, а- нек. число, наз. параболой.
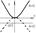 Если вершина нах. в О(0,0), то ур-е примет вид Если вершина нах. в О(0,0), то ур-е примет вид
y2
=2px-симметрично отн. оси ОХ
х2
=2pу-симметрично отн. оси ОУ
Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.
Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2
Св-ва:
1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2
.
25.Эллипс и его св-ва:
Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки
Аx2
+Cy2
=d
ур.-е 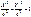
наз. канонич. ур.-ем эллипса, где 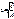 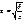 При а=в представляет собой ур-е окружности х2
+y2
=а2 При а=в представляет собой ур-е окружности х2
+y2
=а2
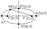
Точки F1
(-c,0) и F2
(c,0) - наз. фокусами эллипса а.
Отношение e=с/а наз. его эксцентриситетом (0<=e<=1)
Точки A1
,A2
,B1
,B2
-вершины эллипса.
Св-во:
Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.
26. Гипербола и ее св-ва.
Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2
+Cy2
=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0
б) Если d>0, то каноническое ур-е гиперболы примет вид: x2
/a2
-y2
/b2
=1, F1(c,o) и F2
(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.
Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.
б) если d=0, ур-е примет вид x2
/a2
-y2
/b2
=0, получаем 2 перекрестные прямые х/а±у/b=0
в) если d<0, то x2
/a2
-y2
/b2
=-1 - ур-е сопряженной гиперболы.
27. Понятие о поверхностях 2го порядка.
Алгебраическим ур-ем 2ой степени наз. ур-е вида Ax2
+Bxy+Cy2
+Dx+ey+F=0, где A,B,C,D,e,F - действительные числа
Линии, которые в системе декартовых координат определяются алгебраическим ур-ем 2ой степени наз. линиями 2го порядка.
28. Функции. Определение способа задания. Классификация функций. Основные элементарные функции.
Функция - это зависимость одной величины от другой.
Если существует взаимооднозначное соответствие между переменной х одного множества и переменной у другого множества, то она называется функциональной зависимостью. y=f(x).
Определение способа задания:
-аналитически (y=kx+b)
-графический (график)
-таблично
-алгоритмически (с помощью ЭВМ)
Классификация функций:
Элементарные:
- функции, которые получаются из основных элементарных ф-ций с помощью алгебраических действий (+,-,*,/,введение в степень). Основные элементарные ф-ции:
1. y=xn
- степенная
2. y=ax
- показательная
3. y=loga
x - логарифмическая
4. y=sinx, y=cosx - тригонометрические.
Сложные:
Y=f(U), где U=j(x), Y=f[j(x)]
Если ф-ция у зависит от промежуточного аргумента U, который зависит от независимой переменной х, то y=f[j(x)] называется сложным заданием х.
29. Определение пределов последовательности и ф-ции. Осн. св-ва пределов ф-ции 1ой переменной.
а) Предел последовательности:
y=f(Un), где U1
,U2
,...Un
, а Un
=n/(n2
+1)
 Предел: число а называется пределом переменной xn
, если для каждого “+” как угодно малого числа e(эпсилон) существует такой номер N, что при n>N разность |xn
-a|<e Предел: число а называется пределом переменной xn
, если для каждого “+” как угодно малого числа e(эпсилон) существует такой номер N, что при n>N разность |xn
-a|<e
limxn
=a
n®¥
-e<Xn
-a<e
a-e<Xn
<a+e
б) Предел ф-ции:
y=f(x) число а называется пределом переменной х, если разность м/ду ними есть б.м.в. |x-a|®0, |x-a|<e
Число А называется пределом ф-ции f(x) при х®а, если для каждого, как угодно малого на период заданного числа e. -e>0, найдется такое как угодно малое на период заданного d>0, что будут выполняться неравенства: Если |x-a|<d, то |f(x)-A|<e
Основные св-ва:
1.Если величина имеет предел, то только 1.
2. limC=C, где С- постоянная величина
3. Если a-б.м.в., то lima=0
4. предела б.б.в. не существует
5. если limy=a, то y=a+a, где a-б.м.в.
30. Основные теоремы о пределах.
1. Предел суммы = суммы пределов:
limx=a, limy=b, тогда x=a+a, y=b+b, где a и b - б.м.в. x+y=(a+a)+(b+b)=(a+b)+(a+b), где a+b=w- б.м.в.
x±y=(a±b)+w, то lim(x±y)=a±b=limx+limy.
2. Теорема о пределе производной: если сомножители имеют пределы, то и произведение имеет предел, равный произведению пределов сомножителей.
limx=a, limy=b, то на основании 5го св-ва
x=a+a
y=b+b, где a и b - б.м.в.
x*y=(a+a)*(b+b)=a*b+(ab+ab+ab), то
сумма б.м.в. = d(дельта)
xy=ab+d
xy®ab,
limxy=ab=limx*limy
3. Следствие: постоянная величина выноситься за знак предела.
limCx=limC*limx=C*limx
4. Предел от частного = частному пределов (кроме limx/limy=0
limx/y=limx/limy, т.к. limx=a, limy=b
x=a+a, y=b+b
x/y=(a+a)/(b+b)
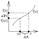
31. 1й, 2й замечательный пределы.
1
й
: limsinx/x=1, limx/sinx=1. x
®
0
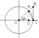 j j
lim((Sina)/a)=1
x®0
SD
OAC
<Sсектора
OAC
<SD
OCB
SD
OAC
=1/2*OC*AD, OA=OC=1, то
SD
OAC
=1/2*OC*OA*Sina=1/2*Sina
Sсектора
OAC
=1/2*OA*OC*a=1/2*a(т.к. OA=OC)
SD
OCB
=1/2*OC*BC=1/2*OC*OC*tga=1/2*tga
1/2*Sina<1/2*a<1/2tga //*2
sina<a<tga//:sin
1<a/sina<1/cosa, =>cosa<sina/a<1,
limCosa<lim((Sina)/a)<lim1, по признаку
a®0 a®0 существования
предела ф-ции
lim((Sina)/a)=1
a®0
2ой: lim(1+1/n)n
=e»2.7183
n®¥
Зная, что 1/n=a - б.м.в., то n=1/a и
x®¥a®0
lim(1+1/n)1/
a
=e
a®0
32. Основные приемы нахождения пределов.
1. Подстановка: при х®х0
и х0
Îобласти определения ф-ции f(x), предел ф-ции f(x)= его частному значению при х=х0
limf(x)=f(x0
)
x®x0
2. Сокращение: при х®¥ и х®х0
f(x)/g(x)=0/0, то сокращают числитель и знаменатель на множитель, стремящийся к 0.
3. уничтожение иррациональности (* числитель и знаменатель на 1 число).
4.деление на наивысшую степень х: при х®¥ и х®х0
f(x)/g(x)=0/0, то делим числитель и знаменатель на наивысшую степень.
5. сведение к известным пределам: lim((Sinx)/x)=1
x®¥
lim(1+1/n)x
=e
x®¥
 33. Непрерывность ф-ции в точке и на интервале. 33. Непрерывность ф-ции в точке и на интервале.
x=x0
+Dx, Dx=x-x0
Dy=f(x0
+Dx)-f(x0
)
Ф-ция y=f(x) наз. непрерывной в точке x0
, если она определена в окрестности этой точки, а limDy=0. (б.м. приращению аргумента соответствует б.м. приращению ф-ции).
limDy=lim[f(x)-f(x0
)]=limf(x)-limf(x0
)=0, то
limf(x)=limf(x0
)
x®x0
Ф-ция непрерывна в точке х0
, если ее предел = значению этой ф-ции в точке х0
Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.
34. Признаки существования а) предела ф-ции и б) предела последовательности.
а) если все значения ф-ции f(x) заключены между значениями ф-ции j(x) и g(x), которые имеют 1 предел при х®а, то и limf(x)=A
j(x)<=f(x)<=g(x), где limj(x)=А, limg(x)=А, то limf(x)=A. х®а
б) Если последовательность монотонно возрастает и ограниченна сверху, то она имеет предел.
Последовательность монотонно возрастает, если последующий член>предыдущего (xn
+1
>xn
)
Последовательность ограничена сверху, если существует такое М, что xn
<=M.
35. Бесконечно малые величины и их св-ва:
величина называется б.м.в. в каком-то процессе, если она в этом процессе бесконечно уменьщается.(r=m/V, если V®¥, то r®0)
Св-ва б.м.в.:
-сумма или разность конечного числа б.м.в. есть б.м.в. (a и b-б.м.в., то a±b=б.м.в.)
-произведение б.м.в. на величину ограниченную есть б.м.в. (U<=M, то a*U=б.м.в.)
-произведение б.м.величин=б.м.в.
-произведение б.м.в. на постоянную = б.м.в
36. Бесконечно большие величины и их св-ва.
б.б.в - величина для которой |Xn
|®¥ (при xn
=1/n, n®0, то xn
®¥)
Св-ва:
-величина обратная б.б.в. явл. б.м.в. (1/¥=0; 1/0=¥)
-сумма б.б.в. (с одинаковым знаком) есть б.б.в.
-произведение 2х б.м.величин=б.м.в.
-частное от деления 2х б.б.в = неопределенность
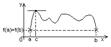
38. Св-ва непрерывных ф-ций:в
в отрезке:
1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.
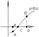 2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке. 2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.
3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке minm и maxM (теорема Вейерштрасса).
в точке:
1. если ф-ция f(x) и g(x) непрерывна в х0
, то их сумма, произведение, частное (при j(х0
)¹0) явл-ся ф-циями, непрерывными в х0
2. если ф-ция y=f(x) непрерывна в х0
, и f(x0
)>0, то существует окрестность х0
, в которой f(x)>0
3. если y=f(U) непрерывна в U0
, а U=j(x) непрерывна в U0
=j(x0
), то сложная ф-ция y=f[j(x)] непрерывна в х0
.
39. Задачи, приводящие к понятию производной. Определение производной и ее геометрический смысл.
1. ncp.
=DS/Dt, n=lim(DS/Dt), гдеDt®0
2. pcp.
=Dm/Dl, pT
=lim(Dm/Dl), гдеDl®0
Dy=f(x+Dx)-f(x), y=f(x)
lim(Dy/Dx)=lim((f(x+Dx)-f(x))/Dx)
Dx®0 Dx®0
Смысл производной - это скорость изменения ф-ции при изменении аргумента.
y=f(x+Dx)-f(x), y=f(x). производной в точке а называется предел отношения приращения ф-ции к приращению аргумента:
lim(Dy/Dx)=lim((f(x+Dx)-f(x))/Dx)=dy/dx
Dx®0 Dx®0
Вычисление производной: lim(Dy/Dx)=y` Dx®0
1) если y=x, Dy=Dx, y`=x=lim(Dy/Dx)=1.
2) если y=x2
, Dy=(x+Dx)2
-x2
=x2
+2xDx+Dx2
-x2
=Dx(2x-Dx),
(x2
)`=lim((Dx(2x+Dx))/Dx)=lim(2x+Dx)=2x
x®0 Dx®0
Геометрический смысл производной.
 KN=Dy, MK=Dx KN=Dy, MK=Dx
DMNK/tg2=Dy/Dx
вычислим предел левой и правой части:
limtga=lim(Dy/Dx) Dx®0
tga0
=y`
a®a0
При Dx®0 секущая MN®занять положение касательной в точке M(tga0
=y`, a®a0
)
Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x0
.
40. Основные правила дифференцирования.
Теорема: Если f(x) и g(x) дифферен. в точке х, то: 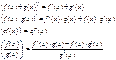
Теорема о произв. сложной функции:
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Теорема о произв. обратной функции.
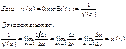
Таблица производных:
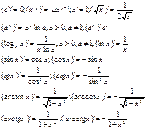
41. Дифференцирование сложных ф-ций:
Производная сложной ф-ции = произведению производной ф-ции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной.
y`=f(x)*U`,или yx
`=yU
`*Ux
`, или dy/dx=dy/dU=dU/dx
Например:
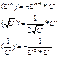
42. Дифференцирование обратной ф-ции.
y=f(x), то x=j(y) - обратная ф-ция.
Для дифференцируемой ф-ции с производной, не = 0, производная обратной ф-ции = обратной величине производной данной ф-ции, т.е. xy
`=1/yx
`.
Dy/Dx=1/(Dy/Dx) - возьмем предел от левой и правой части, учитывая, что предел частного = частному пределов:
lim(Dy/Dx)=1/(lim(Dy/Dx), т.е. yx
`=1/xy
или f`(x)=1/j`(x)
Например:
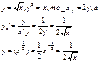
43. Производные степенных и тригонометрических функций.
Основные формулы: 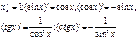
44. Производные обратных тригонометрических функций.
Основные формулы: 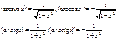
Для сложных функций:
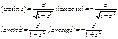
45. Производные показательных и логарифмических функций.
Основные формулы:
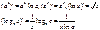
Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:
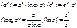
46. Логарифмическое дифференцирование. Вывод производной степенной ф-ции.
y=ax
- показательная ф-ция, y=xn
- степенная, y=xx
- показательно-степенная.
y=[f(x)]j
(
x
)
- показательно-степенная ф-ция.
lny=xlnx - найдем производную от левой и правой части, считая у ф-цией х.
(1/y)*y`=(lny)
(x*lnx)`=x`lnx+x*(lnx)`=lnx+1
y`=y*(lnx+1)=xx
(lnx+1)
Операция, которая заключается в последовательном применении к ф-ции y=f(x) сначала логарифмирование, а затем дифференцирование.
Степенная ф-ция:
1.y=xn
, nlnx, y`/y=n/x=n*(x)-1
y`=y*n*(x-1
)=n*xn
*x-1
=n*xn-1
2.y=eU
, где U=sinx
U`=cosx, y`=(eU
)`=eU
*U`=esinx
*cosx.
47. Производная высших порядков ф-ции 1й переменной.
y=f(x)
y``=(y`)`=lim((f`(x+Dx)-f`(x))/Dx)
x®0
y```=(y``)`= lim((f``(x+Dx)-f``(x))/Dx)
f(n)
(x)=[f(n-1)
(x)]`
48. Производные 1,2-го порядка неявных ф-ций.
Неявной называется такая ф-ция у аргумента х, если она задана уравнением F(x,y)=0, не разрешенным относительно независимой переменной.
y=f(x), y=x2
-1 - явные
F(x,y)=0, a2
=x2
+y2
- неявные ф-ции.
1)a2
=x2
+y2
- найдем производную, продифференцируем, считая у - сложной ф-цией х.
y`=2x+2y=0, т.к. а- постоянная
y*y`=-x, y`=-x/y
2) x3
-3xy+y3
=0
3x3
-3(xy)`+3y2
*y`=0 //:3
x2
-(x`y+y`x)+y2
*y`=0
y`y2
-xy`=y-x2
y`=(y-x2
)/(y2
-x)
49. Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.
limy=A, y=A+a
limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx
Dx®0
Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.
dy=y`Dx
Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.
Если y=x, то dy=dx=x`Dx=Dx, dx=Dx
Если y¹x, то dy=y`dx, y`=dy,dx
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0
,f(x0
)) при изменении x0
на величину Dx
Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)
2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV
3.d(c)=c`dx=0*dx=0
4. d(U/V)`=(V`dU-U`dV)/V2
.
50.Теорема Ролля.
 Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с
из интерв. (a,b), такая, что f’(c)=0. Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с
из интерв. (a,b), такая, что f’(c)=0.
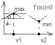 
51
. Теорема Лагранжа.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство:
применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.
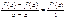

52. Теорема Коши.
Если f(x), g(x) удовл. трем условиям:
1). f(x), g(x) непрерыв. на промеж [a,b]
2). f(x), g(x) деффер. на интервале (a,b)
3). g’(x)¹0 на интер. (a,b), то сущ. т. с
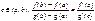
g(b)¹g(a) (неравны по теореме Ролля).
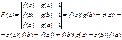
1). F(x) – непрерывна на [a,b]
2). F(x) – деффиренцирована на (a,b)
3). F(a)=0 ; F(b)=0
по теореме Ролля сущ. сÎ(a,b); F’(с)=0
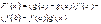
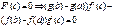
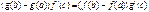
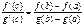
53
. Необходимые и достаточные признаки монотонности ф-ции:
Если x2
>x1
, f(x2
)>f(x1
), то ф-ция монотонно возрастает
Если x2
>x1
, f(x2
)<f(x1
), то ф-ция монотонно убывает
Монотонность - постоянство
Необходимые признаки:1)если ф-ция f(x) всюду в интервале возрастает, то ее производная в этом интервале неотрицательна (f`(x)>=0)
2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x)<=0)
3)если ф-ция f(x) всюду в интервале постоянна, то ее производная в этом интервале =0 (f`(x)=0)
Достаточные признаки монотонности: 1)если f`(x) в интервале положительна, то ф-ция f(x) возрастает в этом интервале.
2)если f`(x)<0, то ф-ция f(x) возрастает в этом интервале.
3)если f`(x)=0, то ф-ция f(x)=const на интервале.
x1
<a<x2
, x2
-x1
>0, x2
>x1
1. если f`(a)>0, то f(x2
)>f(x1
)
2. если f`(a)<0, то f(x2
)<f(x1
)
3. если f`(a)=0, то f(x2
)=f(x1
)
54
. Экстремумы ф-ций. Признаки существования экстремума. Наибольшее и наименьшее значение ф-ции 1й переменной.
Точка х называется точкой max ф-ции, если значение ф-ции в этой точке - наименьшее в некоторой ее окрестности.
1- локальный max
2- локальный min
3- глобальный max
4- глобальный min
если tga>0, то f`(x)>0
если tga<0, то f`(x)<0
Необходимый признак экстремума:ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.
 (В них можно построить ¥ касательных). (В них можно построить ¥ касательных).
Достаточный признак: точка х0
является точкой экстремума, если ее производная в этой точке меняет знак:
- если с “+” на “-”, то х0
- т. max
- если с “-” на “+”, то х0
- т. min
55
. Выпуклость и вогнутость линий точки перегиба.
Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.
Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.
Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.
Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0
Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая
Признаки точки перегиба: чтобы X0
была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х0
.
56. Асимптота графика ф-ции.
Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает.
1) прямая х=х0
назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х0
|f(x)|®+¥ (вида x=b)
2) y=kx+b, ,y=f(x) - общее ур-е наклонной асимптоты
lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б.м.в.) по св-ву x®¥пределов.
разделим левую и правую части на х. Возьмем предел при х®¥
f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x)
x®¥
, то
k=lim(f(x)/x)
b=lim[f(x)-kx]
Если эти пределы существуют, то существует и наклонная ассимптота вида kx+b=y
3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.
57. Предел и непрерывность ф-ции нескольких переменных.
Величина U наз-ся ф-цией переменных (x1
,x2
...xn
), если каждой, рассматриваемой в совокупности этих величин соотв-ет 1 определенное значение величины U.
Пусть f(M)=M0
(x1
0
, x2
0
,... xn
0
), M(x1
, x2
,... xn
)
Ф-ция f(M)=f(x1
, x2
,... xn
) имеет предел А при М0
®М, если каждому значению как угодно малого числа d(дельта) соотв-ет, как угодно малое заданное число e>0, если |M0
M
|=d, то |f(M)-A|<e
Ф-ция f(M) наз-ся непрерывной в точке М0
, если б.м. приращению любого аргумента соответствует б.м. приращение ф-ции.
limf(x1
0
, x2
0
,... xn
0
)=limf(x1
, x2
,... xn
)
x1
0
® x1
x2
0
® x2
xn
0
® xn
58. а) Частная производная ф-ции нескольких переменных. б) Частный и полный дифференциалы.
а) рассмотрим на примере ф-ции 2х переменных
x=f(x,y), точка A(x0
,y0
)
Dz=f(x0
+Dx, y0
+Dy)-f(x0
,y0
) - полное приращение.
Частное приращение по х (по у):
DxZ=f(x0
+Dx, y)-f(x0
, y0
)
DyZ=f(y0
+Dy, x)-f(x0
, y0
)
Частная производная ф-ция:
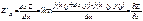 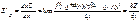 б) dxZ=Zx
`*Dx=¶Z/¶x*dx; dxZ=Zy
`*Dy=¶Z/¶y*dy б) dxZ=Zx
`*Dx=¶Z/¶x*dx; dxZ=Zy
`*Dy=¶Z/¶y*dy
Полный дифференциал dZ=dx
Z+dy
Z=Z`x
dx +Z`y
dy
dZ=¶Z/¶x*dx+=¶Z/¶y*dy
Чтобы найти полный дифференциал ф-ции надо найти частные производные от этой ф-ции по всем независимым переменным, умножить их на дифференциал этих переменных, рез-ты сложить.
59. Производная 2го порядка ф-ции нескольких переменных. Дифференцирование сложной ф-ции 2х переменных.
Частное производной 2го порядка от ф-ции Z явл. частная производная от 1й производной:
Z``XX
=(Z`x
)`x
; Z``yy
=(Z`y
)`y
Z``Xy
=(Z`x
)`y
=(Z`y
)`x
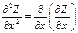
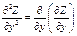
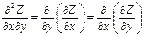
60
. Экстремумы ф-ции нескольких переменных. Необходимые и достаточные признаки экстремума ф-ции 2х переменных.
Z=f(x,y), M0
(x0
,y0
), M(x,y)
Max ф-ции Z называется такое ее значение f(x0
,y0
), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M0
Min ф-ции Z называется такое ее значение f(x0
,y0
), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M0
Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:
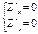
Если Z=f(x1
,x2
,...xn
), то ¶Z/¶xi
=0, i=1,2,...n - необходимое условие.
Достаточный признак:
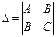
где A= Z``XX
(x0
,y0
), C= Z``yy
(x0
,y0
), B= Z``yx
(x0
,y0
),
1) если D>0, то М0
- точка экстремума;
если А<0 или С<0, то М0
- точка max;
если А>0 или С>0, то М0
- точка min.
2) если D<0, то экстремума нет
3) если D=0, то вопрос о существовании экстремума остается открытым.
61. Общая схема исследования ф-ции необходима для построения графика.
Найти:
-обл. определения ф-ции
-точки разрыва и интервалы, где ф-ция явл-ся непрерывной
-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты
-т. пересечения графика с осями координат
-симметрия графика (чет./нечет):
f(-x)=x симметрична относительно осей
f(-x)=-x симметрична относительно О(0,0)
-периодичность
-интервалы монотонности
-точки экстремума
-наибольшее и наименьшее значение
-выпуклость, вогнутость
-точки перегиба
-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты
-нанесение на график.
|