Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственный технический университет
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебное пособие по математике
для студентов всех специальностей
заочной формы обучения
2007
ФУНКЦИЯ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
Основные определения и понятия
Одним из основных понятий математики является число. Числа целые и дробные, как положительные, так и отрицательные, вместе с числом ноль называются рациональными
числами. Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. Числа, которые представляются в виде бесконечных, но непериодических дробей, называются иррациональными
.
Совокупность всех рациональных и иррациональных чисел называется множеством действительных
, или вещественных
чисел. Действительные числа можно изображать точками числовой оси. Числовой осью
называется бесконечная прямая, на которой выбраны:
1) некоторая точка О, называемая началом отсчёта;
2) положительное направление, указываемое стрелкой;
3) масштаб для измерения длин.
Между всеми действительными числами и всеми точками числовой оси
существует взаимно–однозначное соответствие
, т.е. каждому действительному числу соответствует точка числовой оси и наоборот.
Абсолютной величиной
(или модулем
) действительного числа x
называется неотрицательное действительное число ׀x
׀, определяемое следующим образом: ׀x
׀ = x
, если x
≥ 0, и ׀x
׀ = –x
, если x
< 0.
Переменной величиной
называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной.
Переменная величина называется упорядоченной
, если известна область её изменения и про каждое из двух любых её значений можно сказать, какое из них предыдущее и какое последующее. Частным случаем такой величины является числовая последовательность 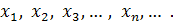
Переменная величина называется возрастающей
(убывающей
), если каждое её последующее значение больше (меньше) предыдущего. Возрастающие и убывающие переменные величины называются монотонными
. Переменная величина называется ограниченной
, если существует такое постоянное число M > 0, что все последующие значения переменной, начиная с некоторого, удовлетворяют условию:
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
– M ≤ x ≤ M, т.е. ׀x
׀ ≤ M.
Переменная величина y называется (однозначной) функцией
переменной величины x, если каждому значению переменной величины x, принадлежащему множеству действительных чисел X, соответствует одно определённое действительное значение переменной величины y
.
Переменная x называется в этом случае аргументом
, или независимой
переменной
, а множество X – областью определения
функции.
Запись y
=
f
(
x
)
означает, что y является функцией x
. Значение функции f
(
x
)
при x
=
a
обозначают через f
(
a
).
Область определения функции в простейших случаях представляет собой: интервал
(открытый промежуток
) (a
,
b
), т.е. совокупность значений x
, удовлетворяющих условию a
<
x
<
b
; сегмент
(отрезок
или замкнутый
промежуток
) 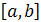 , т.е. совокупность значений x
, удовлетворяющих условию a
≤
x
≤
b
; полуинтервал , т.е. совокупность значений x
, удовлетворяющих условию a
≤
x
≤
b
; полуинтервал
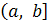 (т.е. a
<
x
≤
b
) или (т.е. a
<
x
≤
b
) или 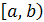 (т.е. a
≤
x
<
b
); бесконечный интервал
(a
,
+ ∞) (т.е. a
<
x
< + ∞) или (– ∞, b
) (т.е. – ∞ < x
<
b
) или (– ∞, + ∞) (т.е. – ∞ < x
< + ∞); совокупность нескольких интервалов или сегментов и т. п. (т.е. a
≤
x
<
b
); бесконечный интервал
(a
,
+ ∞) (т.е. a
<
x
< + ∞) или (– ∞, b
) (т.е. – ∞ < x
<
b
) или (– ∞, + ∞) (т.е. – ∞ < x
< + ∞); совокупность нескольких интервалов или сегментов и т. п.
Графиком
функции y
=
f
(
x
)
называется геометрическое место точек плоскости xOy, координаты которых удовлетворяют уравнению y
=
f
(
x
).
Функция f
(
x
)
называется чётной, если 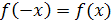 для любого значения x
. График чётной функции расположен симметрично относительно оси ординат. Функция f(x) называется нечётной
, если для любого значения x
. График чётной функции расположен симметрично относительно оси ординат. Функция f(x) называется нечётной
, если 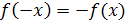 для любого значения x
. График нечётной функции расположен симметрично относительно начала координат. для любого значения x
. График нечётной функции расположен симметрично относительно начала координат.
Функция f
(
x
)
называется периодической
, если существует такое положительное число T, называемое периодом
функции, что для любого значения x
выполняется равенство 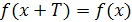 . .
Наименьшим
же периодом
функции называется наименьшее положительное число τ, для которого f
(
x
+ τ) =
f
(
x
)
при любом x
. Следует иметь в виду, что f
(
x
+
k
τ) =
f
(
x
)
, где k
– любое целое число.
Функции задаются:
1) аналитически (в виде формулы), например,  ; ;
2) графически (в виде графика);
3) таблично (в виде таблицы), например таблица логарифмов.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Основными элементарными функциями
являются следующие, аналитически заданные функции:
1. Степенная функция
: 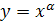 , где α – действительное число. , где α – действительное число.
2. Показательная функция
: 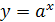 , где a
> 0, a
≠ 1. , где a
> 0, a
≠ 1.
3. Логарифмическая функция
: 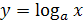 , где a
> 0, a
≠ 1. , где a
> 0, a
≠ 1.
4. Тригонометрические функции
: y
= sinx
,
y
= cosx
,
y
= tgx
,
y
= ctgx
,
y
= sec x, y
= cosec x.
5. Обратные тригонометрические функции
:
y
= arcsin x, y
= arccos x, y
= arctg x, y
= arcctg x, y
= arcsec x
,
y
= arccosecx
.
Если y является функцией от u
, а u
есть функция от x
, то y также зависит от x
. Пусть y
= F(u
), u
= φ(x
). Тогда y
= F(φ(x
)). Последняя функция называется функцией от функции
, или сложной функцией.
Например, y
= sinu
, u
= 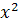 . Функция y
= sin ( . Функция y
= sin (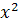 ) есть сложная функция от x
. ) есть сложная функция от x
.
Элементарной функцией
называется функция, которая может быть задана одной формулой вида y
=
f
(
x
)
, где выражение f
(
x
)
составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
Например, y
= ׀x
׀ = 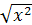 ; ; 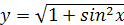 ; ; 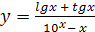 . .
Пример 1
. Найти 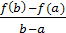 , если , если 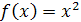 . .
Решение
. Найдём значения данной функции при x
=
a
и x
=
b
:
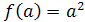 , ,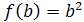 . .
Тогда получим
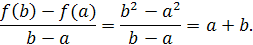
Пример 2
. Определить, какая из данных функций чётная или нечётная:
а) 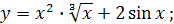 б) б) 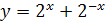 ; в) ; в) 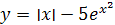 ; ;
г) 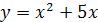 . .
Решение
. а) Так как 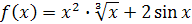 , то , то 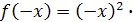
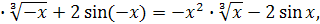 т.е. f
(–
x
) = –
f
(
x
).
Следовательно, функция нечётная. т.е. f
(–
x
) = –
f
(
x
).
Следовательно, функция нечётная.
б) Имеем 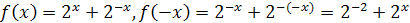 , т.е. , т.е.
f(– x) = f(x). Следовательно, функция чётная.
в) Здесь 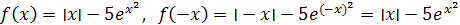 ,т.е. ,т.е.
f
(–
x
) =
f
(
x
).
Следовательно, функция чётная.
г) Здесь 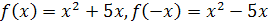 . Таким образом, функция не является ни чётной, ни нечётной. . Таким образом, функция не является ни чётной, ни нечётной.
Пример 3
. Найти область определения функции 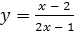 . .
Решение
. Функция 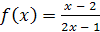 определена, если 2x
– 1 ≠ 0, т.е. если определена, если 2x
– 1 ≠ 0, т.е. если 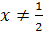 . Таким образом, областью определения функции является совокупность двух интервалов: . Таким образом, областью определения функции является совокупность двух интервалов: 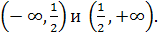
Пример 4
. Найти область определения функции 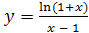 . .
Решение
. Функция определена, если x
– 1 ≠ 0 и 1+ x
> 0, т.е. если x
≠ 1 и x
> – 1. Область определения функции есть совокупность двух интервалов: ( – 1, 1) и (1, + ∞).
Пример 5.
Найти область определения функции
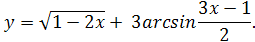
Решение.
Первое слагаемое 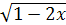 принимает вещественные значения при 1 –2x
≥ 0, а второе при принимает вещественные значения при 1 –2x
≥ 0, а второе при 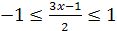 . Таким образом, для нахождения области определения заданной функции необходимо решить систему неравенств: . Таким образом, для нахождения области определения заданной функции необходимо решить систему неравенств: 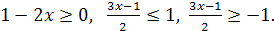 Получаем Получаем 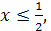
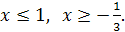 Следовательно, областью определения будет сегмент Следовательно, областью определения будет сегмент
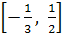 . .
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
При построении графиков функций применяются следующие приёмы:
а) построение «по точкам»;
б) действия с графиками (сложение, вычитание, умножение графиков);
в) преобразования графиков (сдвиг, растяжение).
Исходя из графика функции y
=
f
(
x
)
, можно построить графики функций:
1) y
=
f
(x
–
a
) – первоначальный график, сдвинутый вдоль оси Оx на величину a
;
2) y
=
f
(x
) +
b
– тот же график, сдвинутый вдоль оси Oy на величину b
;
3) y
=
A
·
f
(x
) – исходный график, растянутый в A раз вдоль оси Oy;
4) y
=
f
(kx
) – тот же график, сжатый в k
раз вдоль оси Ox.
Таким образом, можно по графику функции y
=
f
(x
) построить график функции вида 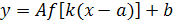 . .
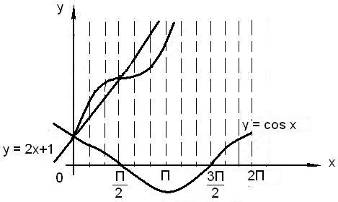
Рис. 1
Пример 6
. Построить график функции y
= 2x
+ 1 + cosx
.
Решение
. График данной функции можно построить путём сложения графиков двух функций: y
= 2x
+ 1, y
= cosx
. График первой функции есть прямая, её можно построить по двум точкам, график второй функции–косинусоида(Рис. 1).
Пример 7
. Построить график функции 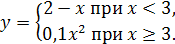
Решение
. При x
< 3 графиком является луч прямой, а при x
≥ 3 – ветвь параболы. Искомый график изображен на рис. 2.
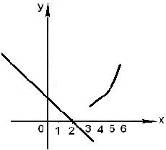
Рис. 2
Пример 8
. Построить график функции y
= 2 sin (2x
– 1) или 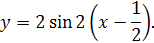
Решение
. Здесь 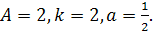 Исходный график y = sinx. Затем строим график функции y = sin 2x путём сжатия вдоль оси абсцисс в два раза. После этого строим график функции Исходный график y = sinx. Затем строим график функции y = sin 2x путём сжатия вдоль оси абсцисс в два раза. После этого строим график функции 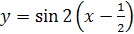 путём сдвига путём сдвига 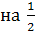 вправо и, наконец, искомый график функции y
= 2 sin (2x
– 1) путём растяжения вдоль оси ординат графика (3) в два раза (рис. 3). вправо и, наконец, искомый график функции y
= 2 sin (2x
– 1) путём растяжения вдоль оси ординат графика (3) в два раза (рис. 3).
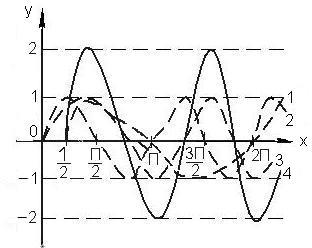
Рис.3
ПРЕДЕЛЫ
Число а
называется пределом последовательности
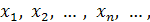 если для всякого сколь угодно малого положительного числа ε найдётся такое положительное число N, что если для всякого сколь угодно малого положительного числа ε найдётся такое положительное число N, что 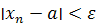 при n
> N. при n
> N.
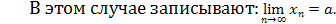
Число A называется пределом функции
f(x) при x → a
, если для любого сколь угодно малого ε > 0 найдётся такое δ > 0, что ׀f
(
x
)
– A׀ < ε при
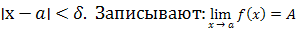 . .
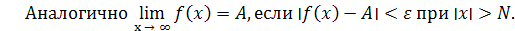
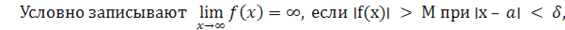
где M – произвольное положительное число .
В этом случае функция f
(
x
)
называется бесконечно большой
величиной при x
→ a
.
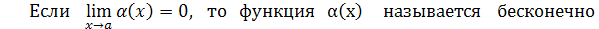
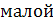 величиной при x
→ a
. величиной при x
→ a
.
Если x
< a
и x
→ a
, то условно пишут x
→ a
– 0; если x
> a
и x
→ a
, то пишут x
→ a
+ 0.
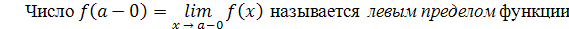
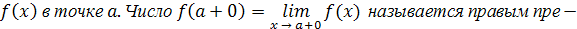
делом
функции f
(x
) в точке a
.
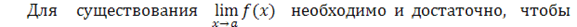
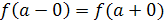
Практическое вычисление пределов основывается на следующих теоремах.
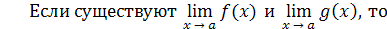
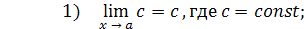
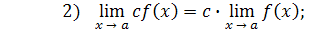
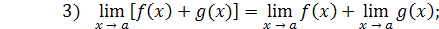
4)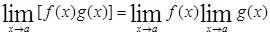
5) 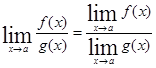 при ( при (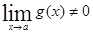 ) )
Используются также первый и второй замечательные пределы:
1)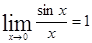
2)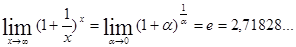
Логарифм числа x
по основанию e
называется натуральным
логарифмом
и обозначается lnx
.
При решении примеров полезно иметь в виду следующие равенства:
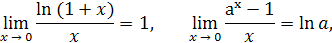
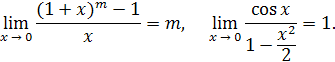
Пример 9
. Показать, что при n
→∞ последовательность 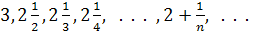 имеет пределом число 2. имеет пределом число 2.
Решение
. Здесь n
–й член последовательности 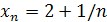 . Следовательно, . Следовательно, 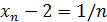 . Зададим заранее положительное число ε. Выберем n настолько большим, что будет выполняться неравенство 1/n
< ε. Для этого достаточно принять n
> 1/ε. При таком выборе n будем иметь . Зададим заранее положительное число ε. Выберем n настолько большим, что будет выполняться неравенство 1/n
< ε. Для этого достаточно принять n
> 1/ε. При таком выборе n будем иметь 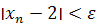 . Следовательно, . Следовательно, 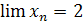 . .
Пример 10
. Показать, что при n
→ ∞ последовательность 7/3, 10/5,
13/7, . . . , (3n + 4) /(2n + 1), . . . имеет пределом число 3/2.
Решение
. Здесь 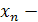 3/2 = (3n + 4) /(2n + 1) – 3/2 = 5/ 3/2 = (3n + 4) /(2n + 1) – 3/2 = 5/ 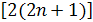 . Определим, при каком значении n выполняется неравенство . Определим, при каком значении n выполняется неравенство
5/ 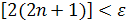 ; так как 2(2n + 1) > 5/ε, то n > 5/4ε – 1/2. ; так как 2(2n + 1) > 5/ε, то n > 5/4ε – 1/2. 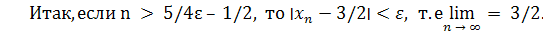
Положив ε = 0,1, заключаем, что неравенство 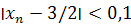 выполняется при n
> 12 (например, при n
= 13). выполняется при n
> 12 (например, при n
= 13).
Неравенство 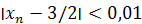 выполняется при n
> 124,5 (например, при n
= 125). выполняется при n
> 124,5 (например, при n
= 125).
Неравенство 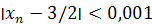 выполняется при n
> 1249,5 (например, при n = 1250). выполняется при n
> 1249,5 (например, при n = 1250).
Пример 11
.
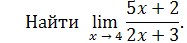
Решение
. Так как x
→ 4, то числитель дроби стремится к числу
5 · 4 + 2 = 22, а знаменатель к числу 2 · 4 + 3 = 11.
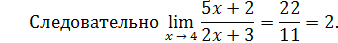
Пример 12
.
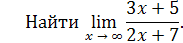
Решение.
Числитель и знаменатель дроби безгранично возрастают при
x
→ ∞. В таком случае говорят, что здесь имеет место неопределённость вида  . .
Разделив на x
числитель и знаменатель дроби, получаем
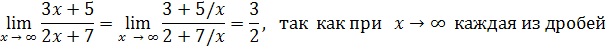
Пример 13
.
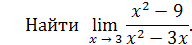
Решение
. Здесь числитель и знаменатель дроби стремятся к нулю при
x
→ 3 (принято говорить, что получается неопределённость вида 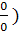 . .
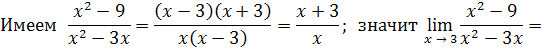
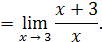
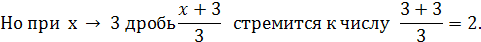
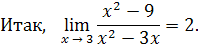
Пример 14
.
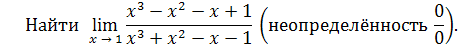
Решение
. Разложим на множители числитель и знаменатель дроби:
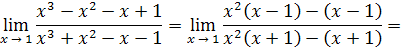
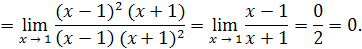
Пример 15
.
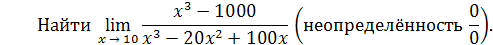
Решение
. Имеем
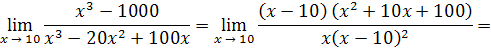
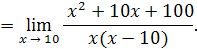
Числитель дроби стремится к 300, а знаменатель стремится к нулю, т.е. является бесконечно малой величиной, следовательно, рассматриваемая дробь –бесконечно большая величина и
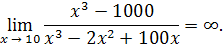
Пример 16
.
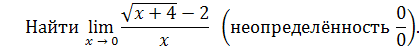
Решение
. Умножим числитель и знаменатель дроби на сумму
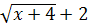 : :
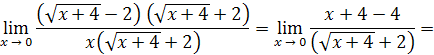
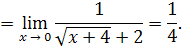
Пример 17
.
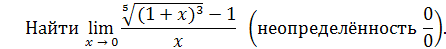
Решение
. Положим 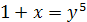 , тогда , тогда
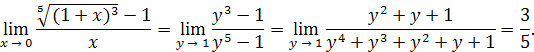
Пример 18
.
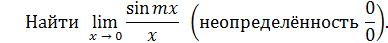
Решение
. Имеем
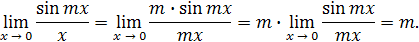
Пример 19
.
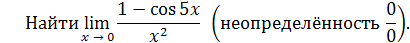
Решение
. Имеем
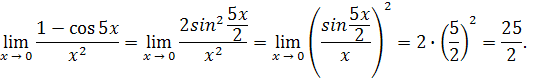
Здесь мы воспользовались результатом предыдущего примера, приняв
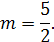
Пример 20
.
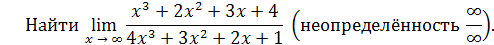
Решение
. Разделим числитель и знаменатель дроби на старшую степень x
, т.е. на 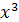 : :
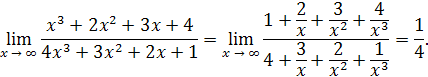
Пример 21
.
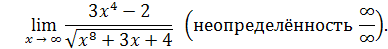
Решение
. Разделим числитель и знаменатель на 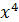 : :
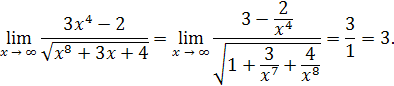
Пример 22
.

Решение
. Умножим и разделим рассматриваемое выражение на
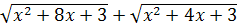 : :
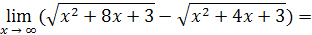
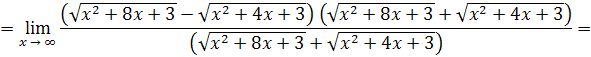
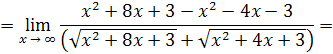
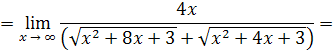
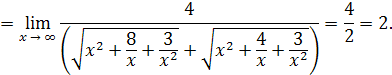
Пример 23.
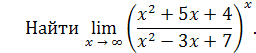
Решение
. Делением числителя дроби на знаменатель выделим целую часть:
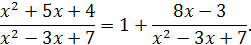
Таким образом,
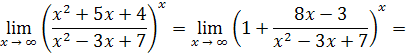
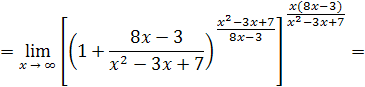
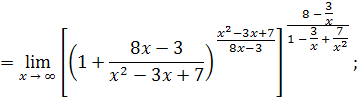
так как
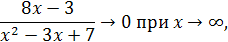
то
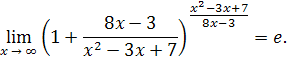
Приняв во внимание, что
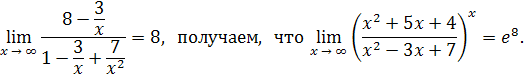
Пример 24
. Найти левый и правый пределы функции
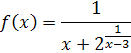
при x → 3.
Решение
.
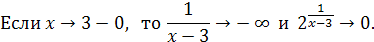
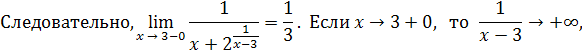
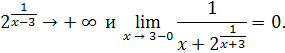
Пример 25
. Найти левый и правый пределы функции 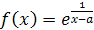 при при
x
→ a
.
Решение
.

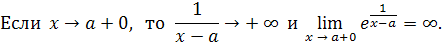
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Функция f(x) называется непрерывной в точке а
, если: 1) эта функция определена в некоторой окрестности точки а
; 2) существует 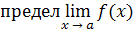 ; 3) этот предел равен значению функции в точке а
, т.е. ; 3) этот предел равен значению функции в точке а
, т.е.
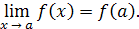
Обозначая 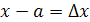 (приращение аргумента) и (приращение аргумента) и 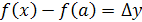 (приращение функции), можно условие непрерывности записать так: (приращение функции), можно условие непрерывности записать так:
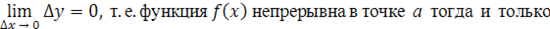
тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области
.
Точка а
, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва
, если в этой точке нарушается условие непрерывности функции.
Если существуют конечные пределы:
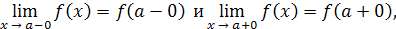
причём не все три числа 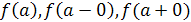 равны между собой, то а
называется точкой разрыва
I рода
. равны между собой, то а
называется точкой разрыва
I рода
.
В частности, если левый и правый пределы функции в точке а
равны между собой: 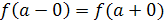 , но не равны , но не равны 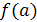 , то а
называется устранимой точкой разрыва
. , то а
называется устранимой точкой разрыва
.
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода
. В точках разрыва II рода не существует хотя бы один из односторонних пределов.
Сумма и произведение конечного числа непрерывных функций есть функция непрерывная.
Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю.
Пример 26
.
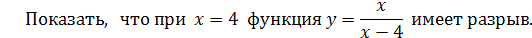
Решение
. Находим
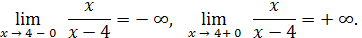
Таким образом, функция при  не имеет ни левого, ни правого конечного предела. Следовательно, не имеет ни левого, ни правого конечного предела. Следовательно,  является точкой разрыва II рода (рис. 4). является точкой разрыва II рода (рис. 4).
Пример 27
.
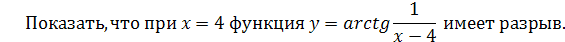
Решение
.
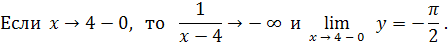
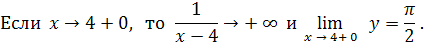
Итак, при 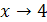 функция имеет левый и правый конечные пределы, причём эти пределы различны. Следовательно, функция имеет левый и правый конечные пределы, причём эти пределы различны. Следовательно, 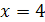 является точкой разрыва I рода. является точкой разрыва I рода.
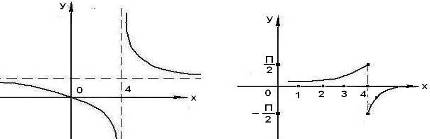
Рис. 4 Рис. 5
Разность между правым и левым пределом в точке разрыва I рода
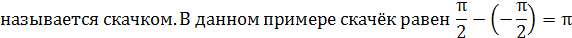
(рис. 5).
Пример 28
.
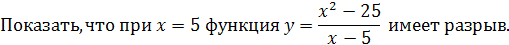
Решение
. В точке 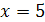 функция не определена, так как, выполнив функция не определена, так как, выполнив
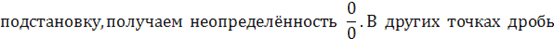
может быть сокращена на 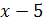 , так как , так как 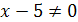 . Следовательно, при . Следовательно, при
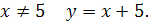 Легко видеть, что Легко видеть, что 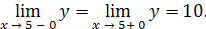
Таким образом, при 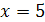 функция имеет устранимый разрыв. Он будет устранён, если условиться, что при функция имеет устранимый разрыв. Он будет устранён, если условиться, что при 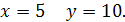
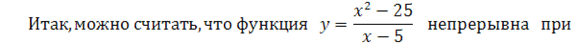

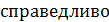 при всех значениях x
,
не исключая и при всех значениях x
,
не исключая и 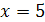 . В этом случае графиком функции будет прямая линия . В этом случае графиком функции будет прямая линия 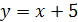 . .
Пример 29
. Доказать, что функция 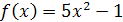 непрерывна в точке непрерывна в точке 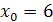 . .
Решение
. Находим 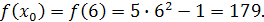
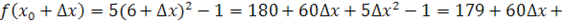
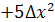 . .
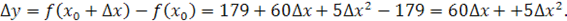
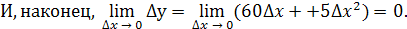
Значит, функция 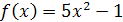 непрерывна в точке непрерывна в точке 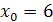 . .
Пример 30
. Исследовать на непрерывность функцию
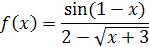
и изобразить график функции в окрестностях точки разрыва.
Решение
. Знаменатель 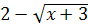 при при 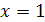 обращается в ноль, и значит, обращается в ноль, и значит, 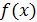 при при 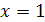 не существует. Следовательно, не существует. Следовательно, 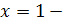 точка разрыва функции. точка разрыва функции.
Для определения типа разрыва надо найти пределы функции слева и справа при 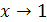 . .
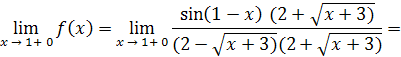
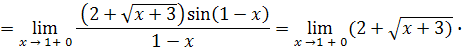
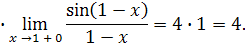
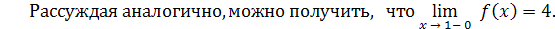
Таким образом, пределы функции слева и справа при 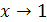 равны между собой, но в точке равны между собой, но в точке 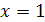 функция не определена, значит, имеем устранимый разрыв. График функции в окрестности точки разрыва изображён на рис. 6 функция не определена, значит, имеем устранимый разрыв. График функции в окрестности точки разрыва изображён на рис. 6
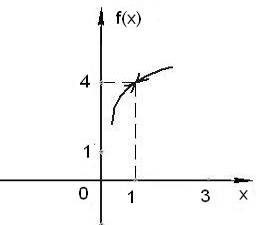
Рис. 6
Доопределив функцию 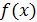 в точке в точке 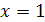 , положив , положив 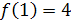 , получим непрерывную функцию , получим непрерывную функцию
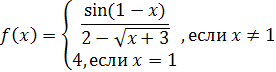
|