Федеральное агенство по образованию
РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ ТЕХНОЛОГИЧЕСКАЯ
АКАДЕМИЯ им. П.А. Соловьева
Факультет: СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ
Кафедра: физики
РЕФЕРАТ
по дисциплине:
«Концепции современного естествознания»
на тему:
«Симметрия в естествознании»
Студент группы ЗКП-09 Большаков Д.Н.
Преподаватель: Гурьянов А.И.
Рыбинск 2009
Содержание
Введение ………………………………………………………………….3
Понятие симметрии………………………………………………………5
Виды симметрии………………………………………………………….6
Симметрия кристаллов…………………………………………………...8
Симметрия пространства……………………………………………… 14
Симметрия времени…………………………………………………… 15
Заключение………………………………………………………………17
Список литературы……………………………………………………...18
Введение
Симметрия – это такая особенность природы, про которую принято говорить, что она охватывает все формы движения и организации материи. Истоки понятия симметрии восходят к древним. Наиболее важным открытием древних было осознание сходства и различия правого и левого. Здесь природными образцами им служили собственное тело, а также тела животных, птиц и рыб.
Вот что написал русский исследователь, ученый ломоносовского склада, энциклопедист В.И. Вернадский в своей работе «Химическое строение биосферы Земли и ее окружения»: «…чувство симметрии и реальное стремление его выразить в быту и в жизни существовало в человечестве с палеолита или даже с эолита, то есть самых длительных периодов в доистории человечества, который длился для палеолита около полмиллиона лет, а для эолита – миллионы лет. Это чувство и связанная с ним работа, еще резко и интенсивно меняясь, сказывались и в неолите 25 000 лет тому назад».
Можно вспомнить также великолепные памятники архитектуры глубокой древности, где пространственные закономерности проявляются особенно ярко. Это храмы древнего Вавилона и пирамиды Гизы, дворец в Ашшуре. Итак, с глубокой древности, начиная, по-видимому с неолита, человек постепенно осознал и пытался выразить в художественных образах тот факт, что в природе, кроме хаотического расположения одинаковых предметов или их частей, существуют некоторые пространственные закономерности. Они могут быть совсем простыми – последовательное повторение одного предмета, более сложными – повороты или отражения в зеркале. Для того, чтобы точно выразить эти закономерности, нужны были специальные термины. По преданию, их придумал Пифагор Регийский.
Реклама

Термином «симметрия», что в буквальном смысле значит соразмерность (пропорциональность, однородность, гармония), Пифагор Регийский обозначил пространственную закономерность в расположении одинаковых частей фигуры или самих фигур. Симметрия может проявляться в перемещениях, поворотах или отражениях в зеркале.
Понятие симметрии
Симметрия – от греческого symmetria, что значит соразмерность – отражает универсальные взаимосвязи объектов мира, выражающиеся одновременно в соотношениях их тождества и различия.
Истоки представлений о симметрии своими глубокими корнями уходят в духовный мир народов Древнего Востока, Греции и Рима.
Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным нарушением определенных видов симметрий. Чтобы это утверждение стало более понятным, рассмотрим подробнее понятие симметрии. «Симметричное обозначает нечто, обладающее хорошим соотношением пропорций, а симметрия – тот вид согласованности отдельных частей, который объединяет их в целое. Красота тесно связана с симметрией», - писал Г. Вейль в своей книге «Этюды о симметрии». Он ссылается при этом не только на пространственные соотношения, т.е. геометрическую симметрию. Разновидностью симметрии он считает гармонию в музыке, указывающую на акустические приложения симметрии.
Зеркальная симметрия в геометрии относится к операциям отражения или вращения. Она достаточно широко встречается в природе. Наибольшей симметрией в природе обладают кристаллы (например, симметрия снежинок, природных кристаллов), однако не у всех из них наблюдается зеркальная симметрия. Известны так называемые оптически активные кристаллы, которые поворачивают плоскость поляризации падающего на них света. В общем случае симметрия выражает степень упорядоченности какой-либо системы или объекта. Например, круг более упорядочен и, следовательно, симметричен, чем квадрат. В свою очередь, квадрат более симметричен, чем прямоугольник. Другими словами, симметрия – это неизменность (инвариантность) каких-либо свойств и характеристик объекта по отношению к каким-либо преобразованиям (операциям) над ним. Например, окружность симметрична относительно любой прямой (оси симметрии), лежащей в ее плоскости и проходящей через центр, она симметрична и относительно центра. Операциями симметрии в данном случае будут зеркальное отражение относительно оси и вращение относительно центра окружности.
Реклама

В широком смысле симметрия
– это понятие, отображающее существующий в объективной действительности порядок, определенное равновесное состояние, относительную устойчивость, пропорциональность и соразмерность между частями целого. Противоположным понятием является понятие асимметрии, которое отражает существующее в объективном мире нарушение порядка, равновесия, относительной устойчивости, пропорциональности и соразмерности между отдельными частями целого, связанное с изменением, развитием и организационной перестройкой. Уже отсюда следует, что асимметрия может рассматриваться как источник развития, эволюции, образования нового. Симметрия может быть не только геометрической. Различают геометрическую и динамическую формы симметрии (и, соответственно, асимметрии). К геометрической форме симметрии
(внешние симметрии) относятся свойства пространства – времени, такие как однородность пространства и времени, изотропность пространства, эквивалентность инерциальных систем отсчета и т.д.
К динамической форме относятся симметрии
, выражающие свойства физических взаимодействий, например, симметрии электрического заряда, симметрии спина и т.п. (внутренние симметрии). Современная физика, однако, раскрывает возможность сведения всех симметрий к геометрическим симметриям.
Виды симметрии
В отличие от искусства или техники, красота в природе не создаётся, а лишь фиксируется, выражается. Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. К числу таких образов относятся некоторые кристаллы, многие растения.
В конформной (круговой) симметрии
главным преобразованием является инверсия относительно сферы. Для простоты возьмём круг радиуса R с центром в точке O. Инверсия этого круга определяется как такое преобразование симметрии, которое любую точку P переводит в точку P', лежащую на продолжении радиуса, проходящего через точку P на расстоянии от центра:
OP'=R2
/ OP
Конформная симметрия обладает большой общностью. Все известные преобразования симметрии: зеркальные отражения, повороты, параллельные сдвиги представляют собой лишь частные случаи конформной симметрии.
Главная особенность конформного преобразования состоит в том, что оно всегда сохраняет углы фигуры и сферу и всегда переходит в сферу другого радиуса.
Известно, что кристаллы какого-либо вещества могут иметь самый разный вид, но углы между гранями всегда постоянны.
Зеркальной симметрии
. Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична. Сначала представляется, что параллельно одной из его сторон могла бы проходить ось симметрии. Но стоит мысленно попробовать воспользоваться ею, как сразу убеждаешься, что это не так. Несимметрична и спираль.
В то время как симметричные фигуры полностью соответствуют своему отражению, несимметричные отличны от него: из спирали, закручивающейся справа налево, в зеркале получится спираль, закручивающаяся слева направо.
Если вы поместите буквы перед зеркалом, расположив его параллельно строке, то заметите, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».
Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф означает
именно истинную середину.
В архитектуре оси симметрии используются как средства выражения архитектурного замысла. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля.
Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
Винтовая симметрия. В пространстве существуют тела, обладающие винтовой симметрией, т.е. совмещаемые со своим первоначальным положением после поворота на какой-либо угол вокруг оси, дополненного сдвигом вдоль той же оси. Если данный угол поделить на 360 градусов - рациональное число, то поворотная ось оказывается также осью переноса.
Симметрия кристаллов
Твердые тела природы существуют в двух формах: аморфной и кристаллической. Аморфные тела представлены стеклами, смолами, пластмассами, к ним могут быть причислены также вар, битумы, воск и т.д. Кристаллические тела – большинство тел природы – пески, глины, базальты, граниты, металлы, большинство минералов природы и химических соединений. Часть из них может существовать в виде монокристаллов - тел с правильной геометрической огранкой (каменная соль, горный хрусталь, медный купорос и др.), значительная часть минералов природы - поликристаллические тела.
Результаты исследований свидетельствуют о том, что в основе структуры у аморфных тел и жидкостей лежит так называемый ближний порядок. Расположение частиц тела обнаруживает определенную тенденцию к упорядочению, тогда как структура кристаллических тел обусловлена наличием дальнего порядка. Расположение частиц тела геометрически упорядочено в пределах всего объема. Его принято отображать с помощью геометрической модели - кристаллической решетки.
Рассмотрение кристаллической структуры твердых тел убеждает, что можно произвольно выделить некоторый наименьший объем (элементарную ячейку), параллельными трансляциями которого можно получить весь кристалл. Таким образом, на первое место в структуре кристаллических тел мы поставим трансляционную симметрию.
В качестве примера рассмотрим простую элементарную ячейку (см. рис.4.2). Она определяется тремя векторами а, в, с
элементарных трансляций и тремя углами a
, b
, g
.

Рис.4.2. Задание элементарной ячейки
Другие свойства симметрии кристаллов отображаются с помощью так называемой решетки Браве.
Решётка Браве выявляет характерные элементы симметрии в расположении одинаковых и одинаково расположенных атомов. Именно этот геометрический образ характеризует симметрию кристаллов относительно операции зеркальной, осевой, центральной, зеркально-поворотной симметрий. Следует иметь в виду, что часто элемент ячейки представляется не одной решеткой Браве, а суперпозицией двух и более. Ниже (рис.4.3–4.9) представлены все возможные типы решеток Браве. Казалось бы, их может быть значительное множество. Однако это не так. Дело в том, что все операции симметрии должны быть совместны с операцией трансляционной симметрии, и это обстоятельство существенно сужает число возможных решеток, ограничивая их количество до 14 типов, объединенных в 7 пространственных групп (сингоний).
Наиболее существенным является то обстоятельство, что в кристаллах исключаются поворотные симметрии пятого порядка, а также поворотные симметрии порядка выше шестого. Исключение симметрии пятого порядка (пентагональной) представляет замечательный факт природы, который обсудим несколько позже.
Следствием симметрии кристаллов является анизотропия их свойств, другими словами, их асимметрия относительно разных направлений внутри кристалла. Поэтому все свойства кристаллов следует разделить на скалярные, которые не зависят от выбора направления, и векторные. К первым можно отнести теплоемкость, теплоту плавления, температуру плавления и т.д.; ко вторым – электропроводность, теплопроводность, механические, оптические, магнитные свойства. Мы видим, что симметрия тесно связана с асимметрией. Тела, более асимметричные по одному физическому свойств, могут оказаться более симметричными по другом.

а) б) в)
Рис.4.3. Решетки кубической системы (a=b=c
; a
=
b
=
g
=90o
):
а) простая; б) объемноцентрированная (ОЦК);
в) гранецентрированная (ГЦК)

а) б)
Рис.4.4. Решетки тетрагональной системы (a=b
¹
c
; a
=
b
=
g
=90o
):
а) простая; б) объемноцентрированная

а) б) в) г)
Рис.4.5. Решетки ромбической системы (а
¹
b
¹
с
, a
=
b
=
g
=90о
): а) простая; б) ОЦК; в) ГЦК; г) базоцентрированная

Рис.4.6. Решетка ромбоэдрической системы

Рис.4.7. Решетки моноклинной системы (a
¹
b
¹
c
; a
=
g
=90o
¹b
):
а) простая; б) базоцентрированная

Рис.4.8. Решетка триклинной системы(a
¹
b
¹
c
; a
¹
b
¹
g
¹90o
)

Рис. 4.9. Решетка гексогональной системы (a=b
¹
c
; a
=
g
=90o
; b
=1200
)
Естественно, возникает законный вопрос: какова же природа симметрии кристаллов? Закономерному расположению частиц в кристалле соответствует минимум энергии частиц, составляющих его, а, следовательно, и состояние устойчивого равновесия. Как известно, устойчивость в диалектике мироздания играет огромную роль, формируя конкретное состояние развивающегося мира. Аморфное состояние вещества является неустойчивым, метастабильным, оно обнаруживает тенденцию к переходу в кристаллическое состояние. Таким образом, симметрия кристаллов выступает как форма, в которой неживая природа выражает тенденцию к своему самосохранению посредством фактора структурности со свойствами симметрии.
Симметрия пространства
Представления о симметрии пространства связаны с непосредственным мироощущением человека, которое формирует представления об эквивалентности всех инерциальных систем отчета и эквивалентности направлений в пространстве. Симметрия пространства в житейских представлениях ассоциируется с его безграничностью, неисчерпаемостью, а реализуется она в форме однородности и в форме изотропности. Однородность пространства выражает инвариантность физических явлений и процессов относительно выбора места их наблюдения. Одинаковый физический эксперимент, поставленный в одинаковых условиях, но в разных лабораториях, приведет к тождественным результатам. Таким образом, однородность пространства предлагает физическую инвариантность процессов, явлений относительно пассивного или активного параллельного переноса системы отсчета. Эквивалентность всех точек пространства предполагает, что при преобразовании 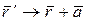 , где , где 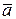 – вектор трансляции, механические свойства любой замкнутой механической системы остаются неизменными. – вектор трансляции, механические свойства любой замкнутой механической системы остаются неизменными.
Пусть материальные точки с массами m1
, m2
, .... , mn
составляют замкнутую механическую систему ;  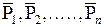 – импульсы каждого из тел, составляющих эту систему; – импульсы каждого из тел, составляющих эту систему; 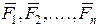 – силы, с которыми тела системы действуют на отдельное тело m1
, m2
и т.д. соответственно. Вследствие однородности пространства расстояния между телами системы – силы, с которыми тела системы действуют на отдельное тело m1
, m2
и т.д. соответственно. Вследствие однородности пространства расстояния между телами системы 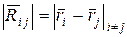 , относительные скорости , относительные скорости 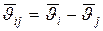 остаются неизменными при преобразовании остаются неизменными при преобразовании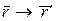 , а, следовательно, остаются неизменными и внутренние силы , а, следовательно, остаются неизменными и внутренние силы 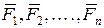 . Именно поэтому . Именно поэтому 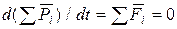 , откуда и следует известный закон сохранения импульса для замкнутой механической системы: , откуда и следует известный закон сохранения импульса для замкнутой механической системы: 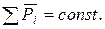
Сохранение импульса – отображение однородности пространства. Другой аспект симметрии пространства связан с изотропностью пространства. Это фундаментальное свойство пространства выражается в эквивалентности всех направлений в нем. Действительно, мы наблюдаем системы двойных звезд, плоскости движения которых некоторым образом ориентированы относительно плоскости эклиптики, однако физические законы, действующие во всех случаях, одни и те же.
Представим себе однородное массивное сферическое тело. Его гравитационное поле будет обладать сферической симметрией. Любые возможности движения другой материальной частицы в нем описываются одним математическим аппаратом и характерной ситуацией для такой задачи является сохранение векторной величины 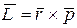 , называемой моментом импульса. В этом выражении , называемой моментом импульса. В этом выражении 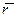 – радиус-вектор частицы относительно центрального тела, – радиус-вектор частицы относительно центрального тела, 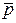 – ее импульс. Сохранение момента импульса является отображением изотропности пространства. – ее импульс. Сохранение момента импульса является отображением изотропности пространства.
Симметрия времени
Симметрия пространства, пожалуй, наиболее противоречивая из всех возможных симметрий. Она отражает сложную логику взаимоотношений прошлого, настоящего, будущего. Эта симметрия определяет мотивацию нашей деятельности сегодня, определяет границы жизненности прошлого опыта и его переноса в настоящее, а также переноса настоящего в будущее. Она так же как и симметрия пространства имеет 2 аспекта. Первый из них - однородность времени - выражается в том, что один и тот же эксперимент, поставленный в разных исторических условиях, приводит к одному и тому же результату. Мы можем воспроизвести любой опыт Ньютона или Фарадея и воспроизвести их результаты. Физически такая возможность обусловлена фундаментальным законом движения материи – законом сохранения энергии. Другой аспект симметрии проявляется в симметрии законов развития процессов относительно инверсии времени t
®- t
. Так, в задачах динамики, когда сила 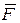 зависит только от относительных расстояний между телами системы, основное уравнение движения тела зависит только от относительных расстояний между телами системы, основное уравнение движения тела 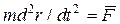 инвариантно относительно преобразования t
®- t
. Именно это обстоятельство позволяет нам восстановить хронологию событий по известным документальным данным астрономических явлений: затмений Луны, Солнца, вспышек сверхновых звезд и т.д. инвариантно относительно преобразования t
®- t
. Именно это обстоятельство позволяет нам восстановить хронологию событий по известным документальным данным астрономических явлений: затмений Луны, Солнца, вспышек сверхновых звезд и т.д.
Другие примеры симметрии связаны, в частности, с волновым уравнением Даламбера
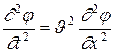 , ,
где j
– параметр, определяющий волновой процесс (сдвиговое смещение, давление, мгновенное значение плотности в точке с координатой х
в момент времени t
); 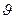 – скорость процесса. Замена t
на - t
не влияет на характер процесса. Аналогичный случай – колебания упругой балки – скорость процесса. Замена t
на - t
не влияет на характер процесса. Аналогичный случай – колебания упругой балки 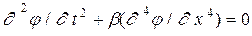 , где , где 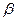 – коэффициент упругости. Но как показывает нам жизненный опыт, нет симметрии между прошлым и будущим, процессы, как правило, необратимы. Таким образом, симметрии времени сопутствует его асимметрия. Единство симметрии и асимметрии, их взаимопроникновение является всеобщим, универсальным. – коэффициент упругости. Но как показывает нам жизненный опыт, нет симметрии между прошлым и будущим, процессы, как правило, необратимы. Таким образом, симметрии времени сопутствует его асимметрия. Единство симметрии и асимметрии, их взаимопроникновение является всеобщим, универсальным.
Заключение
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира
Еще одним интересным проявлением симметрии жизненных процессов являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука - хронобиология.
Помимо симметрии существует также понятие ассиметрии:
Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.
Список литературы:
1.
Карпенков С.Х. Концепции современного естествознания.М.:”ЮНИТИ”,1997
2. «Симметрия в природе», И.И. Шафрановский, Ленинград «недра», 1985г.
3.
«Кристаллы», М.П. Шаскольская, Москва «наука», 1978г.
4. Грядовой Д.И. Концепции современного естествознания. Структурный курс основ естествознания. – М.: Учпедгиз, 1999.
5. Дубнищева Т.Я. Концепции современного естествознания. – Новосибирск: ЮКЭА, 1997.
6. Концепции современного естествознания./ под ред. проф. С.А. Самыгина, 3-е изд. – Ростов н/Д: «Феникс», 2002.
7. Найдыш В.М. Концепции современного естествознания.- М.: АЛЬФА-М, ИНФРА-М.-2003
8. «Концепция современного естествознания» под ред. проф. Лаврененко. Москва, «Просвещение», 1997г.
9. Миронов А. В. «Концепции современного естествознания». – ПЗ Пресс, 2003.
10. Солопов «Концепция современного естествознания» Москва, «Владас», 1997-2002г.
|