Задача 1.
Построить графики функций с помощью производной первого порядка.
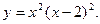
1) 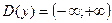 . .
2) Функция ни четная, ни нечетная.
3) 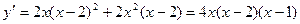 . .
При  , , 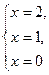

(0;0)- точка минимума,
(2;0)- точка минимума,
(1;1)- точка максимума.

Задача 2.
Построить графики функций с помощью производной первого порядка.
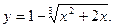
1) 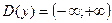 . .
2) Функция ни четная, ни нечетная.
3) 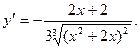
При  , , 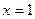 ; ; 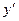 не существует в точках не существует в точках 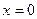 и и 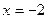 . .

(-1;2)- точка максимума.

Задача 3.
Найти наибольшее и наименьшее значения функций на заданных отрезках.
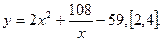
ОДЗ 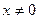 . .
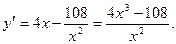
При  , , 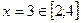 ; ;
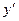 не существует при не существует при 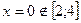 . .
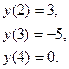
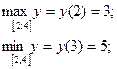
Задача 4.
При подготовке к экзамену студент за 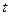 дней изучает дней изучает 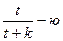 часть курса, а забывает часть курса, а забывает 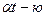 часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса? часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?
k=1/2, 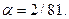
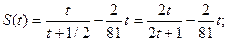
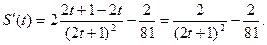
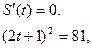
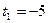 не удовлетворяет условию задачи. не удовлетворяет условию задачи.
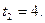
Точка 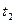 является точкой минимума. является точкой минимума.
Ответ:
4 дня.
Задача 5.
Исследовать поведение функций в окрестностях заданных точек с помощью производных высших порядков.
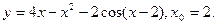
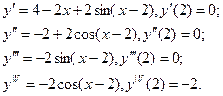
Т.к. 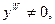 то в точке то в точке 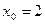 функция имеет максимум. функция имеет максимум.
Задача 6.
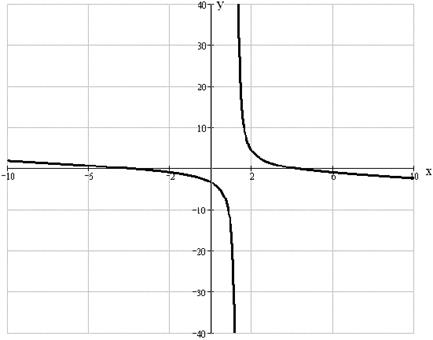
Найти асимптоты и построить графики функций.
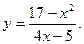
1) 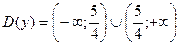 . .
2) Функция ни четная, ни нечетная.
3)
а) 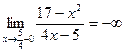 , ,
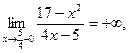
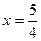 -вертикальная асимптота. -вертикальная асимптота.
б)  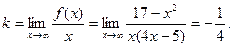
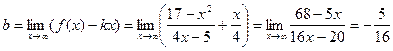 . .
Следовательно, 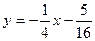 - наклонная асимптота. - наклонная асимптота.
4) 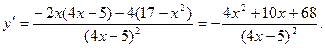
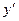 не существует при не существует при 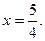
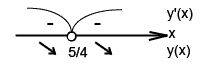
5) Найдем точки пересечения с осями:
При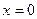 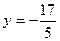 . .
При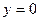 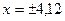 . .
Задача 7.
Провести полное исследование функций и построить их график.
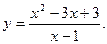
1) 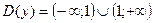 . .
2) Функция ни четная, ни нечетная.
3)
а) 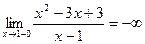 , ,
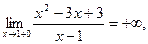
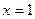 -вертикальная асимптота. -вертикальная асимптота.
б)  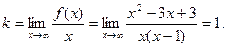
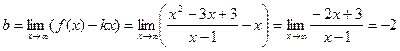 . .
Следовательно, 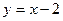 - наклонная асимптота. - наклонная асимптота.
4) 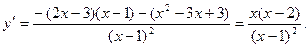
 при при 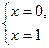
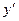 не существует при не существует при 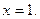

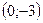 -точка максимума функции. -точка максимума функции.
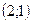 -точка минимума функции. -точка минимума функции.
5) 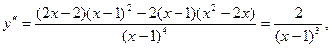
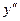 не существует при не существует при 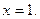
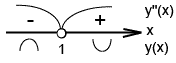
6) Найдем точки пересечения с осями:
При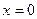 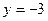 . .
При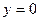 квадратное уравнение не имеет корней, следовательно график не пересекается с осью квадратное уравнение не имеет корней, следовательно график не пересекается с осью 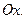
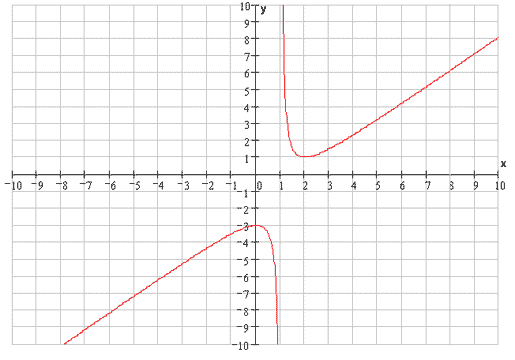
Задача 8.
Провести полное исследование функций и построить их графики.
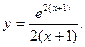
1) 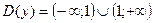 . .
2) Функция ни четная, ни нечетная.
3)
а) 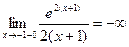 , ,
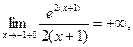
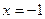 -вертикальная асимптота. -вертикальная асимптота.
б)  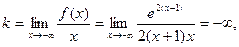
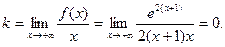
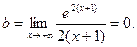 . .
Следовательно, 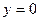 - горизонтальная асимптота. - горизонтальная асимптота.
4) 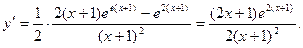
 при при 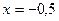 , ,
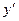 не существует при не существует при 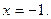
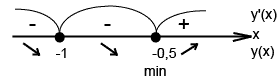
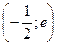 -точка минимума функции. -точка минимума функции.
5) 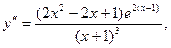
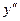 не существует при не существует при 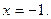
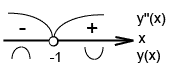
6) Найдем точки пересечения с осями:
При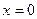 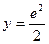 . .
При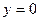 квадратное уравнение не имеет корней, следовательно график не пересекается с осью квадратное уравнение не имеет корней, следовательно график не пересекается с осью 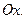
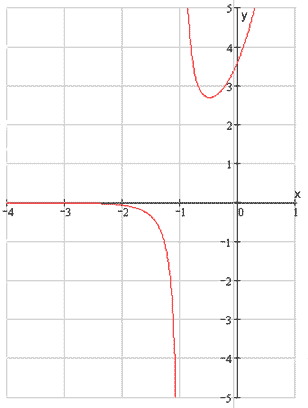
Задача 9.
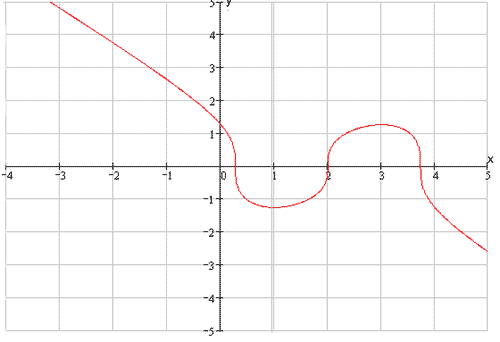
Провести полное исследование функций и построить их графики.
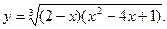
1) 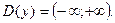
2) Функция ни четная, ни нечетная.
3)
а) вертикальных асимптот нет.
б)  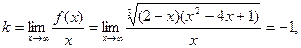
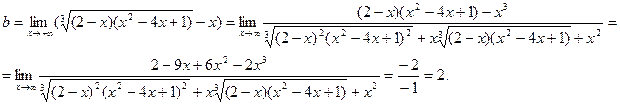 . .
Следовательно, 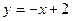 - наклонная асимптота. - наклонная асимптота.
4) 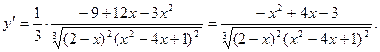
 при при 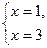 , ,
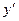 не существует при не существует при 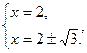
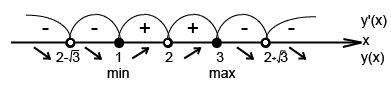
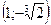 -точка минимума функции, -точка минимума функции,
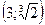 - точка максимума функции. - точка максимума функции.
5) 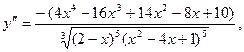
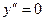 при при 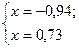 , ,
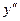 не существует при не существует при 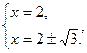
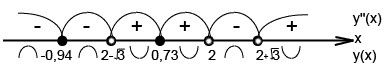
6) Найдем точки пересечения с осями:
Реклама

При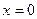 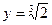 . .
При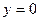 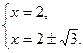
Задача 10.
Провести полное исследование функций и построить их графики.

1) 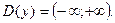
2) Функция ни четная, ни нечетная.
3)
а) вертикальных асимптот нет.
б) наклонных асимптот нет.
4) функция является периодической
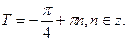
5) 
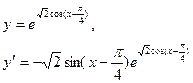
 ,тогда ,тогда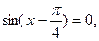
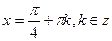 . .
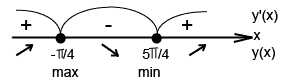
6)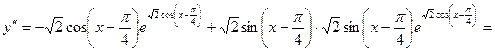
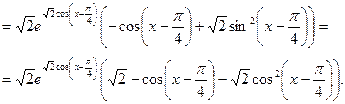
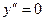 при при 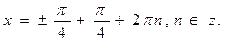 , ,
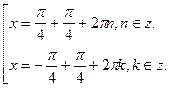
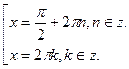
При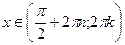 функция вогнута, т.к. функция вогнута, т.к. 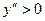 . .
При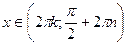 функция выпукла, т.к. функция выпукла, т.к. 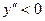 . .
Точки перегиба:
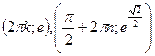 . .
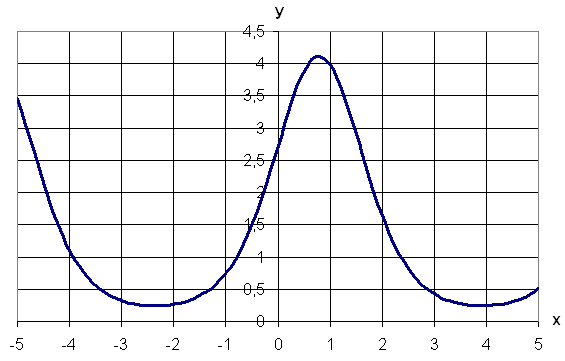
|