Міністерство освіти і науки України
Національний технічний університет
“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ"
Кафедра “Обчислювальної техніки та програмування"
Реферат з курсу “Численные методы"
Тема: “Решение уравнений в конечных разностях”
Виконав:
студент групи
Перевірив:
Харків
Содержание
1. Разностная аппроксимация дифференциальных уравнений
2. Решение линейных разностных уравнений
3. Рекуррентные формулы для решения разностных уравнений
4. Интерполяционные рекуррентные формулы
4.1 Интерполяция конечными разностями “назад”
4.2 Рекуррентные формулы Адамса
Литература
Используя описанные выше соотношения между операторами дифференцирования и операторами конечных разностей несложно в заданном интервале изменения независимой переменной получить конечно-разностную аппроксимации дифференциальных уравнений системой алгебраических рекуррентных формул или уравнений. Основная идея аппроксимации схематически представляется так: В заданном в общем виде дифференциальном уравнении или системе
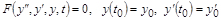
производится замена независимой переменной t
ее представлением в заданном интервале 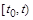 путем преобразования путем преобразования 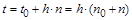 , а искомая функция и ее производные выражаются посредством конечно-разностных соотношений через некоторое число равномерно расположенных с шагом , а искомая функция и ее производные выражаются посредством конечно-разностных соотношений через некоторое число равномерно расположенных с шагом 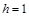 ординат ординат 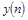 , начиная с , начиная с 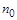 : : 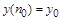 , , 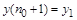 , , 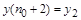 ,..., ,..., 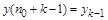 : : 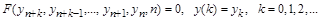 . .
Разрешив неявную форму разностного выражения относительно старшей ординаты 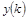 , получим рекуррентную формулу, из которой по известным k
начальным ординатам можно последовательно найти ординаты всего искомого процесса. Вопрос лишь в том, где взять нужное количество начальных ординат. Благополучно разрешима задача лишь в случае, когда производная аппроксимируется разностью первого порядка: , получим рекуррентную формулу, из которой по известным k
начальным ординатам можно последовательно найти ординаты всего искомого процесса. Вопрос лишь в том, где взять нужное количество начальных ординат. Благополучно разрешима задача лишь в случае, когда производная аппроксимируется разностью первого порядка:
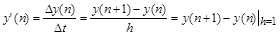 . .
После приведения исходной системы к системе уравнений первого порядка каждая искомая переменная получает значение при 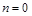 , равное своему начальному условию. В результате рекуррентный вычислительный процесс оказывается определенным и позволяет вычислить на очередном шаге , равное своему начальному условию. В результате рекуррентный вычислительный процесс оказывается определенным и позволяет вычислить на очередном шаге 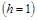 значения всех переменных: значения всех переменных:
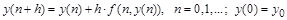
или
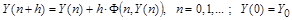
где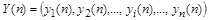 - вектор переменных, - вектор переменных,
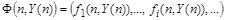 - вектор производных. - вектор производных.
Такой вычислительный процесс в литературе получил название численного интегрирования систем дифференциальных уравнений по явному методу Эйлера. Основная трудность здесь заключается в выборе шага интегрирования для нецелочисленной независимой переменной t
.
Реклама

Система линейных разностных уравнений может быть в ряде случаев решена и аналитически. Решение представляется в виде алгебраического выражения от целочисленной переменной. Методика решения аналогична той, что применяется и при решении линейных дифференциальных уравнений.
Используется тот факт, что общее решение неоднородного линейного уравнения представляется взвешенной суммой системы фундаментальных решений однородного уравнения и одного частного решения уравнения неоднородного. Воздействие неоднородности на характер общего решения не связано с конкретными значениями начальных условий. Именно это позволяет находить лишь одно частное решение уравнения с правой частью. Число фундаментальных решений однородного уравнения определяется порядком последнего.
В качестве частных решений для линейных уравнений обычно используют функции, инвариантные по отношению к операции сдвига, т.е. функции, не изменяющие своей структуры при переносе начала координат. В конечно-разностных уравнениях это показательные функции:
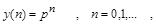
Где p - некоторый параметр-константа. Количество частных решений определится числом параметров 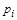 , для которых , для которых 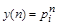 будет обращать разностное уравнение в тождество. Общее решение составляется в виде суммы частных решений, умноженных на коэффициенты, определяемые конкретными начальными условиями. Рассмотрим пример решения линейного неоднородного уравнения третьего порядка. будет обращать разностное уравнение в тождество. Общее решение составляется в виде суммы частных решений, умноженных на коэффициенты, определяемые конкретными начальными условиями. Рассмотрим пример решения линейного неоднородного уравнения третьего порядка.
Пусть требуется заменить рекуррентный вычислительный процесс с псевдокодом следующего вида:
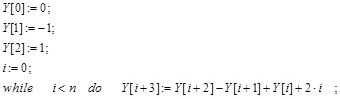
на формульное выражение для 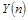 , как функции от n,
позволяющее выборочно вычислять значение любого члена последовательности. Для этого в рекуррентном операторе цикла заменим оператор ': =' на символ равенства '=' и запишем полученное уравнение в форме неоднородного разностного уравнения относительно , как функции от n,
позволяющее выборочно вычислять значение любого члена последовательности. Для этого в рекуррентном операторе цикла заменим оператор ': =' на символ равенства '=' и запишем полученное уравнение в форме неоднородного разностного уравнения относительно 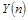 : :
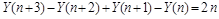 .
.
В качестве фундаментальной системы функций возьмем 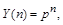 тогда характеристическое уравнение примет следующий вид: тогда характеристическое уравнение примет следующий вид:
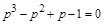 . .
Решив уравнение, найдем корни:  , следовательно, частными решениями однородного уравнения будут: , следовательно, частными решениями однородного уравнения будут:
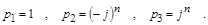
Частное решение неоднородного уравнения (с правой частью) попробуем найти в виде функции, которая будет пропорциональна квадратуре от правой части с неизвестными коэффициентами:
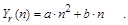
Для нахождения коэффициентов a
и b
подставим в уравнение 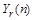 и приравняем коэффициенты при одинаковых степенях n
в левой и правой частях полученного равенства. Последовательно выполняя сказанное, имеем: и приравняем коэффициенты при одинаковых степенях n
в левой и правой частях полученного равенства. Последовательно выполняя сказанное, имеем:
Реклама

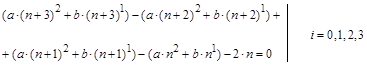
Раскрыв скобки и сгруппировав слагаемые при различных степенях n
, получим
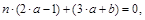
откуда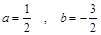 и частное решение примет вид и частное решение примет вид
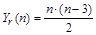 . .
Общее решение для конкретных начальных условий ищем в виде суммы частных решений:
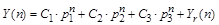 . .
Константы 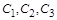 находим из уравнений, получаемых после подстановки в общее решение значений для находим из уравнений, получаемых после подстановки в общее решение значений для 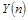 при при 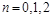 : :
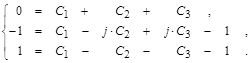
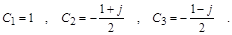
В результате, общее решение неоднородного уравнения будет:
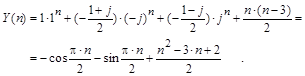
Для примера выпишем несколько первых членов ряда, полученных вычислением этого выражения: [0, - 1, 1, 2, 2, 5, 11, 16, 20, 27, 37, 46, 54, 65, 79, 92, 104, 119, 137, 154, 170,...]
Интегрирование системы нелинейных разностных уравнений первого порядка по Эйлеру аналитически выполнить, как правило, не удается. Поэтому решение задачи получают в численном виде путем вычисления очередных значений процессов по рекуррентным формулам, начиная с известных начальных условий:
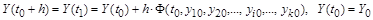 , ,
Где 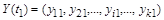 - очередное значение вектора решений, - очередное значение вектора решений,
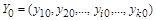 - вектор начальных значений. - вектор начальных значений.
Основной проблемой процесса численного интегрирования является выбор величины шага h
. Формула Эйлера вносит в процесс численного решения погрешность, пропорциональную h.
Это несложно увидеть, если сравнить вычисляемое при интегрировании уравнения выражение с первыми слагаемыми ряда Тейлора для точки 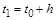 : :
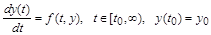 . .
По Эйлеру
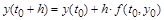 , ,
или иначе:
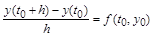 , ,
а по Тейлору:
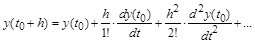 , ,
или иначе:
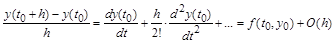 . .
Отбрасываемые члены разложения 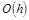 характеризуют погрешность формулы Эйлера, в которую входят слагаемые с h
в первой степени и выше. характеризуют погрешность формулы Эйлера, в которую входят слагаемые с h
в первой степени и выше.
Результат интегрирования можно улучшить, если по найденному значению 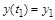 , , 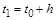 вычислить значение производной, т.е. вычислить значение производной, т.е. 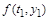 , и в формулу Эйлера ввести среднее арифметическое двух производных: для начала и для конца интервала , и в формулу Эйлера ввести среднее арифметическое двух производных: для начала и для конца интервала 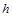 . Модифицированная формула примет следующий вид: . Модифицированная формула примет следующий вид:
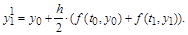
Такого рода уточнения (итерации) можно повторять, пока в выражении
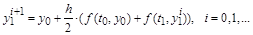 модуль разности станет модуль разности станет 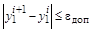 . .
Погрешность модифицированной формулы будет пропорциональна 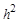 . Это показывается аналогично предыдущему сопоставлению. . Это показывается аналогично предыдущему сопоставлению.
Продифференцируем исходное уравнение
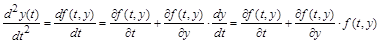
и подставим выражение производной в ряд Тейлора. В результате получим:
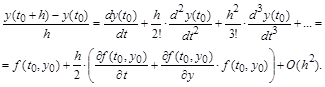
Аналогичное выражение для первых двух слагаемых и остаточного ряда второй степени от h
получается и для модифицированной формулы Эйлера, если в последней осуществить разложение 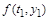 в ряд Тейлора по степеням h
: в ряд Тейлора по степеням h
:
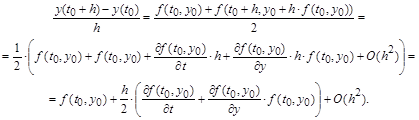
Усреднение производных с итерационным уточнением их для нескольких точек интервала особенно наглядно представлено в формулах Рунге-Кутта четвертого порядка 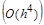 : :
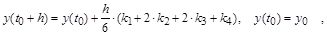
где
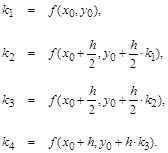
Здесь производная вычисляется в трех точках интервала h
(на концевых точках и дважды в средней точке интервала для итерационного уточнения), после чего окончательное приращение находится как взвешенное среднее.
Достоинством методов Эйлера и Рунге-Кутта является их самоначинаемость независимо от порядка формулы, а основной недостаток в том, что число вычислений правой части неоднородной системы дифференциальных уравнений равно порядку формулы.
В этом плане выгодно отличаются формулы интегрирования, построенные на основе интерполяционных многочленов, опорными точками которого являются предыдущие, уже вычисленные значения переходного процесса. Широко используемым методом интегрирования с таким подходом могут служить формулы интегрирования Адамса.
Возьмем в качестве примера интерполяционный многочлен Ньютона для интерполирования функции “назад”, т.е. в сторону меньших значений независимой переменной по отношению к текущему ее значению:
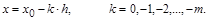
Построение такого интерполяционного многочлена удобно осуществлять с применением повторных конечных разностей “назад”:
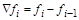 . .
Взаимосвязь оператора 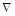 и рассмотренных выше операторов и рассмотренных выше операторов 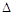 и и 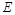 характеризуется следующими соотношениями: характеризуется следующими соотношениями:

Выразим ординату функции, отстоящую от текущей на k
шагов назад, через ординату функции 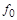 в текущей точке и выполним ряд эквивалентных преобразований с названными линейными операторами: в текущей точке и выполним ряд эквивалентных преобразований с названными линейными операторами:
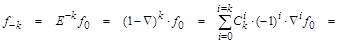
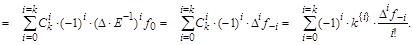
Если положить
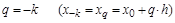 , то , то
 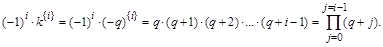
Таким образом, интерполяционный многочлен Ньютона для интерполирования “назад” принимает вид:
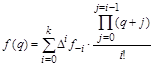 , ,
где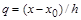 принимает целые значения для принимает целые значения для 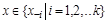 , ,
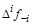 - i-
тая повторная конечная разность “вперед", вычисляемая по значениям функции в соответствии с таблицей: - i-
тая повторная конечная разность “вперед", вычисляемая по значениям функции в соответствии с таблицей:
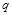 |
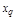 |
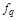 |
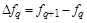 |
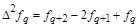 |
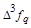 |
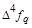 |
| -4 |
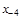 |
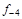 |
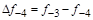 |
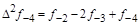 |
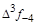 |
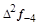 |
| -3 |
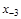 |
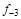 |
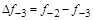 |
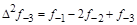 |
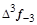 |
- |
| -2 |
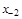 |
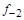 |
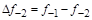 |
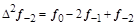 |
- |
- |
| -1 |
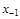 |
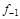 |
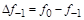 |
- |
- |
- |
| 0 |
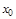 |
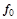 |
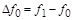 |
- |
- |
- |
| 1 |
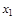 |
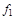 |
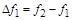 |
- |
- |
- |
В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона.
Пусть теперь требуется найти решение уравнения
 . .
для которого уже каким-либо способом найдены k
+1 значений решения 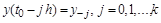 , что, естественно, определяет и соответству-ющие значения , что, естественно, определяет и соответству-ющие значения 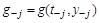 . На основе . На основе 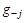 построим интерполя-ционный многочлен k-
той степени: построим интерполя-ционный многочлен k-
той степени:
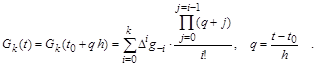
Приращение решения на внешнем интервале 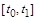 можно получить, проинтегрировав интерполяционный многочлен в интервале можно получить, проинтегрировав интерполяционный многочлен в интервале 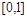 по переменной q
, предварительно сделав замену переменных: по переменной q
, предварительно сделав замену переменных:
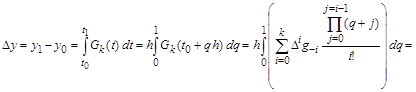
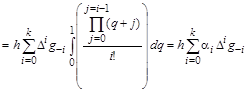 . .
Интегралы в каждом слагаемом зависят только от i
и определяют коэффициенты, с которыми повторные разности входят в выражение для приращения. Таким образом, экстраполяционная формула Адамса имеет вид:
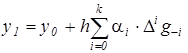 , ,
где первые пять коэффициентов приведены в таблице
Появление нового значения 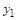 требует для очередного шага вычислить новые значения повторных разностей. Для этого в таблице разностей заполняется по одной дополнительной клеточки в каждом столбце после одного-единственного вычисления правой части. В этом и состоит основное достоинство экстраполяционных формул. требует для очередного шага вычислить новые значения повторных разностей. Для этого в таблице разностей заполняется по одной дополнительной клеточки в каждом столбце после одного-единственного вычисления правой части. В этом и состоит основное достоинство экстраполяционных формул.
В формулу Адамса вместо повторных разностей можно подставить их выражения через ординаты  . Например, ограничившись . Например, ограничившись 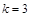 , получим , получим
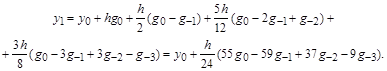
Модификаций у формул Адамса много. Можно менять не только интерполяционные многочлены, но и вычислять приращения в пределах нескольких шагов. Наиболее простой получается формула для k
=4, в которой приращение вычисляется на интервале в два шага 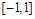 : :
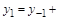 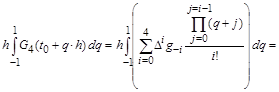
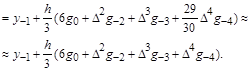
Если построить интерполяционный многочлен Ньютона не от точки 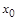 , а от точки , а от точки 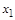 и опять вычислить для k
=4 приращение в интервале и опять вычислить для k
=4 приращение в интервале 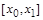 , то последнее может служить контролем за точностью вычислений: , то последнее может служить контролем за точностью вычислений:
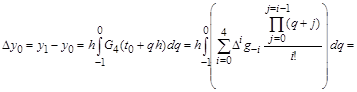
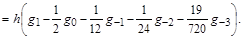
1. Беллман Р., Кук К. Дифференциально-разностные уравнения. М.: Мир, 1967. - 548с.
2. Волков Е.А. Численные методы. СПб.: Лань, 2004. - 248с.
3. Гельфонд А.О. Исчисление конечных разностей. М.: Наука, 1967. - 375с.
4. Калашников В.И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. - Харьков: НТУ “ХПИ", 2002. - 196с.
5. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. Новосибирск: Изд-во иностр. лит., 1958. - 474с.
6. Скалкина М.А., “О колебаниях решений уравнений в конечных разностях", Изв. вузов. Матем., 1959, № 6, 138-144
|