 Постановка транспортной задачи общего вида Постановка транспортной задачи общего вида
Классическая постановка транспортной задачи общего вида такова.
Имеется m пунктов отправления («поставщиков») и n пунктов потребления («потребителей») некоторого одинакового товара. Для каждого пункта определены:
ai
– объемы производства i -го поставщика, i = 1, …, m;
вj
– спрос j-го потребителя, j= 1,…,n;
сij
– стоимость перевозки одной единицы продукции из пункта Ai
– i-го поставщика, в пункт Вj
– j-го потребителя.
Для наглядности данные удобно представлять в виде таблицы, которую называют таблицей стоимостей перевозок.
| Потребители Поставщики |
В1
|
В2
|
… |
Вn
|
запасы |
| А1
|
С11
|
C12
|
C1n
|
а 1
|
| А2
|
С21
|
C22
|
C2n
|
а2
|
| … |
| Am
|
Cm1
|
Cm2
|
Cmn
|
а m
|
| Потребности |
в1
|
в2
|
в n
|
Требуется найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные транспортные расходы были бы минимальными.
Под планом перевозок понимают объем перевозок, т.е. количество товара, которое необходимо перевезти от i-го поставщика к j-му потребителю. Для построения математической модели задачи необходимо ввести m·n штук переменных хij
, i= 1,…, n, j= 1, …, m, каждая переменная хij обозначает объем перевозок из пункта Ai в пункт Вj. Набор переменных X = {xij
} и будет планом, который необходимо найти, исходя из постановки задачи.
 Ограничения задачи примут вид: Ограничения задачи примут вид:

Это условие для решения закрытых и открытых транспортных задач (ЗТЗ).
Очевидно, что для разрешимости задачи 1 необходимо, чтобы суммарный спрос не превышал объема производства у поставщиков:
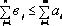
Если это неравенство выполняется строго, то задача называется «открытой» или «несбалансированной», если же 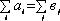 , то задача называется «закрытой» транспортной задачей, и будет иметь вид (2): , то задача называется «закрытой» транспортной задачей, и будет иметь вид (2):
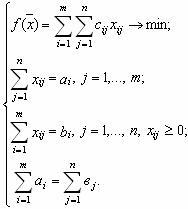
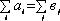 – условие сбалансированности. – условие сбалансированности.
Это условие для решения закрытых транспортных задач (ЗТЗ).
В силу ограничений нетрудно увидеть, что ЗТЗ является задачей ЛП и может быть решена симплекс-методом после приведения ее к специальному виду. Но структура системы ограничений имеет некоторою специфику, а именно:  каждая переменная х ij
входит ровно два раза в неравенства системы, и все переменные входят в неравенства системы с коэффициентом 1. В силу этой специфики существует более простой метод решения, называемый методом потенциалов, который, по сути, является некоторой модификацией симплекс-метода. По-прежнему идеей является переход от одного опорного плана к другому, обязательно «лучшему» с точки зрения значения целевой функции. Каждому опорному плану также соответствует своя распределительная таблица. Переход осуществляется от одного плана к другому, пока полученный план не будет удовлетворять условию оптимальности. Необходимо научиться строить первоначальный опорный план. В качестве первоначального плана годится любое решение системы уравнений (2). Заметим, что это система линейных уравнений, состоящая из m + n уравнений с m*n неизвестными. Можно доказать, что линейно независимых уравнений в системе (2) m + n – 1, ввиду условия сбалансированности, т.е. базисных переменных должно быть m + n– 1. Итак, в качестве плана будем представлять себе таблицу размера m ∙ n, в которой должно быть занято m + n – 1 клеток, отвечающих базисным переменным xij
. каждая переменная х ij
входит ровно два раза в неравенства системы, и все переменные входят в неравенства системы с коэффициентом 1. В силу этой специфики существует более простой метод решения, называемый методом потенциалов, который, по сути, является некоторой модификацией симплекс-метода. По-прежнему идеей является переход от одного опорного плана к другому, обязательно «лучшему» с точки зрения значения целевой функции. Каждому опорному плану также соответствует своя распределительная таблица. Переход осуществляется от одного плана к другому, пока полученный план не будет удовлетворять условию оптимальности. Необходимо научиться строить первоначальный опорный план. В качестве первоначального плана годится любое решение системы уравнений (2). Заметим, что это система линейных уравнений, состоящая из m + n уравнений с m*n неизвестными. Можно доказать, что линейно независимых уравнений в системе (2) m + n – 1, ввиду условия сбалансированности, т.е. базисных переменных должно быть m + n– 1. Итак, в качестве плана будем представлять себе таблицу размера m ∙ n, в которой должно быть занято m + n – 1 клеток, отвечающих базисным переменным xij
.
Реклама

Построение первоначального опорного плана по правилу наименьшей стоимости
Построение плана по правилу наименьшей стоимости заключается в следующем. Рассматриваем матрицу (таблицу) транспортных расходов, стоимостей, данную изначально в качестве условия задачи. Выбираем клетку с минимальной ценой перевозки (клетка с номером i, j) и помещаем в эту клетку наименьшее из чисел {ai
, bj
}. Затем исключаем из рассмотрения строку, соответствующую поставщику (если аi
меньшее), или столбец, соответствующий потребителю (если в j меньшее). Исключение строки означает, что запасы i-го потребителя удовлетворены. Из оставшейся таблицы снова выбираем наименьшую стоимость, и т.д. продолжаем до тех пор, пока все запасы не исчерпаны, а потребности не удовлетворены. Проверьте, что сумма чисел в каждой строке получившейся таблицы равна а i, а сумма чисел в каждом столбце равна вj
, что и требовалось. Число занятых клеток должно равняться m + n – 1, в противном случае, если занятых клеток меньше, чем m + n – 1, дополним таблицу необходимым количеством нулей (нулевых перевозок) и будем считать эти клетки с нулями занятыми так, чтобы общее количество занятых клеток равнялось равноm + n – 1. Нули поставим в клетки, соответствующие минимальной стоимости.
 Метод потенциалов Метод потенциалов
При построении плана мы ставим задачу найти хоть какой-нибудь, не обязательно лучший, оптимальный план, удовлетворяющий ограничениям задачи. Теперь нам хотелось бы уметь отвечать на вопрос: является ли найденный опорный план оптимальным, и если нет, то «улучшать» его. Эту задачу решает метод потенциалов, предложенный в 1949 г. советскими учеными Л.В. Канторовичем и М.К. Гавуриным. теоретической основой метода является теорема.
Реклама

Теорема. Если для некоторого опорного плана Х = { xij
} транспортной задачи можно подобрать систему из m + n чисел u1
, u2
, …, um
, v1
, v2
, … vn
, называемых потенциалами, то план оптимален тогда и только тогда, когда выполняются условия:
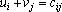 для всех xij
> 0 для всех xij
> 0
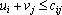 для всех i = 1,m, j = 1,n для всех i = 1,m, j = 1,n
где (cij
) – матрица стоимостей перевозок.
Доказательство теоремы опускаем, оно основывается на рассмотрении двойственной задачи к исходной транспортной. Итерация метода потенциалов состоит из трех шагов.
I шаг (вычисление потенциалов).
Условие (1) представляет собой систему из ( m + n – 1) линейных уравнений с (m + n) неизвестными потенциалами. Поэтому одно из неизвестных полагаем равным 0 для определенности, затем последовательно находим остальные потенциалы.
II шаг (проверка плана на оптимальность).
Для проверки плана на оптимальность необходимо проверить условие (2). Для занятых клеток это условие выполняется, именно на них достигается равенство. Остается посчитать суммы ui + vj
для свободных клеток. Если ui
+ vj
≤ сij
, то, по теореме, план является оптимальным и задача решена.
 III шаг (улучшение плана). III шаг (улучшение плана).
Для проведения операции улучшения плана нам понадобится понятие цикла.
Определение. Циклом будем называть набор клеток матрицы перевозок, в котором две и ровно две соседние клетки расположены в одной строке или в одном столбце, и первая и последняя клетки набора лежат тоже в одной строке или столбце.
Графически нетрудно представить цикл в виде ломаной, каждое звено которой лежит в строке или в столбце, причем в каждой строке или столбце не более чем по одному звену.
Примеры:
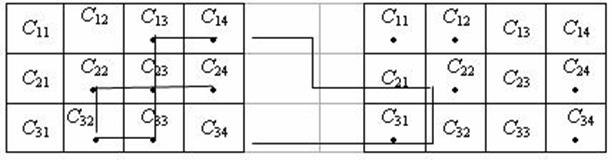
С понятием цикла связаны важные свойства планов:
допустимый план является опорным, когда из занятых этим планом клеток нельзя образовать ни одного цикла;
если имеем опорный план, то для каждой свободной клетки можно образовать единственный цикл, содержащий данную клетку и некоторые из занятых.
Улучшение плана производится по следующей схеме. В подчеркнутых клетках табл. 2 находим клетку с наибольшей разностью ui
+ vj
– cij
, т.е. где условие (2) нарушается максимально.
Затем для этой клетки, согласно утверждению 2, строим единственный цикл. Набор клеток в цикле помечаем поочередно знаками «+» и «–», начиная с «+» в свободной клетке.
Начиная с клетки (1, 1), где условие (2) нарушено максимально, строим цикл. Клетку (1, 1) помечаем знаком «+». Цикл единственен, у нас все занятые  клетки вошли в цикл, но это необязательно. Строим новый план хn
по правилу: клетки вошли в цикл, но это необязательно. Строим новый план хn
по правилу:

Замечание. Если транспортная задача является задачей открытого типа, в которой условие баланса не выполняется, а именно сумма запасов больше суммы потребностей, то решить такую задачу можно по предложенной схеме методом потенциалов, введя дополнительного потребителя, с потребностью равной разности балансов и нулевыми стоимостями перевозок от каждого поставщика к этому потребителю.
|