| Міністерство освіти і науки України
Вінницький національний технічний університет
Інститут автоматики, електроніки та комп’ютерних систем управління
Факультет автоматики та
комп’ютерних систем управління
Кафедра автоматики та
інформаційно-вимірювальної техніки
КУРСОВА РОБОТА
з дисципліни: “Моделювання на ЕОМ”
за темою: “ ДОСЛІДЖЕННЯ ОДНОКРОКОВИХ МЕТОДІВ
РОЗВ’ЯЗАННЯ ЗВИЧАЙНИХ ДИФЕРЕНЦІЙНИХ РІВНЯНЬ ”
Виконала __________ _______________
ст. гр. 1АМ-01 Баковська Н.О.
Перевірив __________ _______________
ст. викладач Кабачій В.В.
2004 р.
АНОТАЦІЯ
В данній курсовій роботі розглядаються методи чисельного розв’язання звичайних диференціальних рівнянь з початковими умовами. Ілюстрацією є програма на мові Паскаль, що знаходить таблицю значень шуканої функції за простим, виправленим та удосконаленим методами Ейлера з оцінкою похибки
ЗМІСТ
Зміст
Вступ.
1. Теоретичні відомості
2. Огляд та аналіз методів розв`язання системи диференціальних рівнянь, вибір методів рішення
3. Блок-схема алгоритму
3.1. Алгоритми методів Ейлера
3.2. Алгоритм головної програми
4. Результати роботи програми
Висновки
Використані джерела інформації
ВСТУП
Головним методом дослідження складних процесів та систем сьогодні став обчислювальний експеримент, що оснований на побудові та аналізі комп’ютерної моделі об’єкта, який вивчається.
Метод математичного моделювання дозволяє виключити необхідність виготовлення громіздких фізичних моделей, зв'язану з матеріальними витратами; скорочувати час визначення характеристик (в особливості при розрахунку математичних моделей на ЕОМ і застосуванні ефективних обчислювальних методів і алгоритмів ); вивчати поводження об'єкта моделювання при різних значеннях параметрів; аналізувати застосовність різних елементів ; одержувати характеристики і показники; які складно знімати експерементально (кореляційні , частотні, параметричної чутливості).
Дана курсова робота й має на меті надати початкових навичок у математичному моделюванні та у вирішені задач обчислювальної математики.
1. ТЕОРЕТИЧНІ ВІДОМОСТІ
Постановка задачі
Звичайне диференціальне рівняння має безліч рішень. Для відшукання якого-небудь конкретного рішення вимагаються додаткові умови. Ці умови можуть бути різними. У випадку, коли додаткові умови задаються при одному значенні незалежної зміною, має місце задача Коші (задача з початковими умовами). Якщо ж умови задаються при двох чи більш значеннях незалежної змінної, то задача називається крайовию. У задачі Коші додаткові умови називаються початковими, а в крайовій-краєвими. При рішенні цих задач використовуються різні методи й алгоритми.
Реклама

Сформулюємо задачу Коші.
Нехай дане диференціальне рівняння
у' = f (x, y);
і початкова умова y(0)=у
. Потрібно знайти систему точок на відрізку від х=а
до х=b
з кроком h ,
що задовольняє як вказаному рівнянню, так і початковій умові (при цьому завжди передбачається, що існує єдине рішення на усьому відрізку).
Крайову задачу розглянемо на прикладі звичайного диференціального рівняння другого порядку
y” = f (x, y, у' )
при граничних умовах у(а)=А, у(b)=В.
Методи рішення рівнянь більш високих порядків аналогічні.
Вибір методу рішення задачі Коші.
При порівнянні ефективності однокрокових і багатокрокових методів можна виділити наступні особливості.
1. Багатокрокові методи вимагають великого обсягу пам'яті ЕОМ, тому що оперують великою кількістю вихідних даних.
2. При використанні багатокрокових методів існує можливість оцінки погрішності на кроці. Тому величина кроку вибирається оптимальної, а в однокрокових з деяким запасом, що знижує швидкодію.
3. При порівнянні точності багатокрокові методи вимагають великого обсягу обчислень. Наприклад, застосовуючи метод Рунге-Кута четвертого порядку точності, доводиться обчислити чотири значення функції на кожнім кроці, а для забезпечення збіжності методу прогнозу і корекції того ж порядку точності - два.
4. Однокрокові методи, на відміну від багатокрокових, дозволяють почати рішення задачі (самостартування) і легко змінити крок у процесі рішення.
Перед початком рішення задачі необхідно зробити перевірку на <жосткість> і у випадку позитивного результату застосувати спеціальні методи. Якщо задача Коші дуже складна, то звичайна перевага віддається методу прогнозу і корекції, що володіє до того ж більш високим швидкодією. Початок рішення задачі при цьому виробляється за допомогою однокрокових методів. Якщо для обчислення чергового значення yi
потрібно більше двох ітерацій, чи якщо помилка відсічення занадто велика, то необхідно зменшити величину кроку h
. З іншого боку, при дуже малій погрішності усікання можна збільшити крок, тим самим підвищивши швидкодію, але при цьому весь процес рішення виробляється спочатку. Іноді на практиці потрібно мінімізувати час підготовки задачі до рішення. Тоді доцільно використовувати методи Рунге-Кута.
Реклама

2. ОГЛЯД ТА АНАЛІЗ МЕТОДІВ РОЗВ`ЯЗАННЯ СИСТЕМИ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ, ВИБІР МЕТОДІВ РІШЕННЯ.
Методи рішення задачі Коші
В основі чисельних методів рішення диференціальних рівнянь лежить розклад функції в
у ряд Тейлора в околі вихідної точки х0
:
Y(X0 + H )=Y(X0) + HY
¢
(X0 )
+ 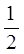 H2 Y
¢¢
(X0 )+
…. + H2 Y
¢¢
(X0 )+
…. + 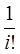 Hi Yi (X0 ), Hi Yi (X0 ),
де h-відстань
(крок) між вихідною точкою х0
і точкою х1=х0+h, у якій відшукується рішення.
Причому в різних методах враховується різна кількість членів розкладання (у багатокрокових методах у сполученні з інтерполяційними формулами), що визначає точність обчислень. Вважають, що порядок помилки дорівнює р
. В методах Ейлера вона визначається з співвідношення:
Δ≤ch2
де с=(М1+M0 M2 )/2, М0 ,M1 , M2 -- визначаються як
М0≥│f(x,y)
│;
М1≥│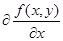 │; │;
М2≥│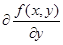 │; │;
Число С
не залежить від номера кроку і його величини, а визначається похідними і довжиною інтервалу. При апроксимації рішення рядами Тейлора воно зв'язано зі ступенем членів ряду, що відкидаються.
Методи рішення задачі Коші можна розділити на дві групи: однокрокові, у яких для перебування наступної точки на кривій у=f(х)
потрібна інформація лише про один попередній крок (методи Ейлера і Рунге-Кута); багатокрокові (прогнозу і корекції), у яких для знаходження слідуючої точки на кривій у=f(х)
потрібно інформація більш ніж про одну з попередніх точок. Для одержання досить точного чисельного значення часто використовується ітераційна процедура (наприклад, у методах Мілна, Адамса-Башфорта і Хеммінга).
Однокрокові методи.
Найбільш простим однокроковим методом, що вимагає мінімальних ресурсів, але володіє порівняно низкою точністю, є метод Ейлера.
Рішення диференціальних рівнянь
Геометричне тлумачення цього методу полягає в тому, що він апроксимує графік рішення диференціального рівняння дотичної до графіка в точці (t0, x0) (рисунок 2.1). Цей метод називається однокроковим, тому що процедура одержання оцінки рішення в деякій точці складається з одного кроку. Похибка простого методу Эйлера досить велика, отже, він потребує модифікації.
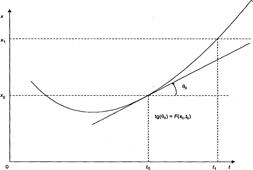
Рисунок 2.1.Крок методу Ейлера
Модифікований метод Эйлера (відомий також як метод Хьюна) — це двухкроковий процес (рисунок 2.2).
Простий метод Ейлера в ньому використовується для побудови першого наближення в точці. У цій точці визначається тангенс кута нахилу дотичної до графіка функції. Для одержання остаточної оцінки в точці виробляється усереднення тангенсів кута нахилу в обох крапках. Очевидно, у цьому випадку вимагаються дві оцінки функції Р(х):
S1 = F(t0,x0), z = x0+s1 dt,
S2 = F(t1,z), x1 =x0+(s1+s2)dt/2.
Рисунок. 2.2. Крок модифікованого методу Ейлера. Жирною лінією показано використовуване наближення.
В цьому методі для оцінки наступної точки на кривій y = f (x) використовується тільки один лінійний член в формулі Тейлора.
Метод Ейлера, крім значної похибки часто буває нестійкий (малі локальні похибки приводять до значного збільшення глобальної)
Ще більш висока точність може бути досягнута при обчисленні вищих похідних і збереженні більшого числа членів ряду Тейлора. Такими методами є методи Рунге - Кутта.
Метод Рунге - Кутта дає набір формул для розрахунку координат внутрішніх крапок, необхідних для реалізації цієї ідеї. Оскільки існує ряд способів перебування цих точок, метод Рунге — Кутта поєднує сімейство методів для рішення диференціальних рівнянь першого порядку. Частіше інших використовується класичний метод — метод четвертого порядку точності
У загальному випадку метод Рунге - Кутта
є n-кроковим методом. На інтервалі [t0,t1
] мається послідовність п
точок, і для цих точок обчислюються нахили дотичних до графіка функції. Одержавши кілька значень, ми використовуємо їх зважене середнє для побудови відрізка лінії, що йде з початкової точки. Робиться це для того, щоб обчислити оцінку рішення в наступній точці. Потім обчислюється нахил у цій точці і т.д. Це - геометричне тлумачення методів Рунге-Кутта. Читач може самостійно побудувати малюнок, аналогічний малюнкам для методу Ейлера. Можна дати і більш строге формулювання. Нехай задані числові коефіцієнти аi, by, i
= 2, ..., т, j =
1, ..., т—
1,
sk, k =
1, ..., т
і послідовно обчислюються функції
k = F(tn,xn),
k2 =F(tn + a2 h, xn +b21 hk1),
k3 =F(tn + a3 h, xn +b31 hk1 +b32 hk2 ),
---------------------------------------------
k = F(t +ah, x + bhk+bhk+...+bhk ).
Потім з формули
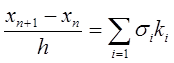
знаходиться значення хn+1 = х(tn+1).
Числові коефіцієнти вибираються з розумінь точності, методи Рунге-Кутта розрізняються способом вибору цих коефіцієнтів. Помітимо, що методи Рунге-Кутта при m> 5 не використовуються.
У розрахунках звичайно роблять слідуючим чином. Інтервал, на якому необхідно знайти наближене рішення диференціального рівняння, розбивають на кілька інтервалів меншого розміру, і на кожнім такому інтервалі застосовують метод Ейлера чи будь-який інший з названих чисельни0х методів рішення диференціальних рівнянь. У підсумку одержують, якщо знову звернутися до мови геометричних побудов, ламану, котра досить (чи недостатньо!) добре наближає графік точного рішення диференціального рівняння (рисунок 2.3).
Розглянемо загальні риси однокрокових методів.
1. Для одержання інформації в новій точці потрібні дані лише про одній попередній точці.
2. В основі всіх однокрокових методів лежить розкладання функції в ряд Тей лора, у якому зберігаються члени, содержащі h
у ступені до k
включно. Ціле число і називається порядком методу. Погрішність на кроці має порядок k
+1.
3. Однокрокові методи не вимагають обчислення похідних - обчислюється лише функція, але може знадобитися її значення в декількох проміжних точках.
4. Можливість зміни величини кроку обчислень.
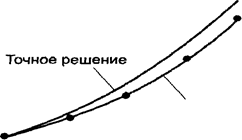
Рисунок. 2.3. Відповідність між наближеним і точним рішеннями диференціального рівняння
3. БЛОК-СХЕМА АЛГОРИТМУ
3.1 Алгоритми методів Ейлера
В розробленій програмі використовуються окремі алгоритми для кожного методу та алгоритм головної програми. Таким чином є 4 основних алгоритми. Розглянемо їх.
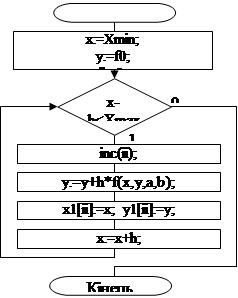
Рисунок 3.1.Алгоритм простого методу Ейлера
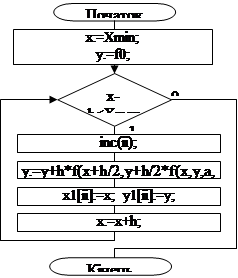
Рисунок 3.2.Алгоритм виправленого методу Ейлера
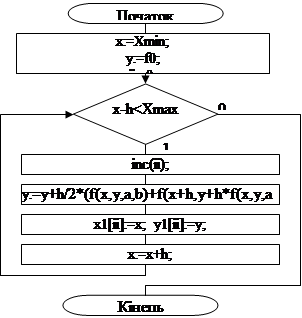
Рисунок 3.3.Алгоритм модифікованого методу Ейлера
Як бачимо алгоритми майже однакові, різниця тільки в формулі обчислення наступного члена.
3.2 Алгоритм головної програми
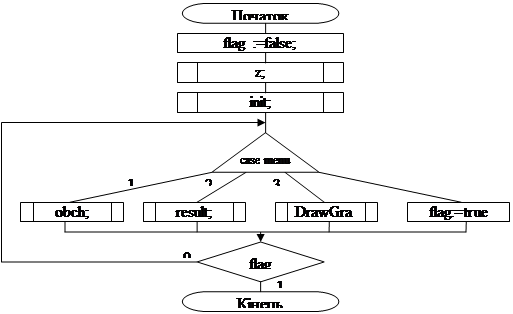
Рисунок 3.4. Алгоритм головної програми
Головна програма складається з двох частин (рисунок 3.4). Перша частина програми складається з процедури-заставки z
та процедури ініціалізації графічного режиму init
для зображення меню. Друга частина розміщена в циклі і виконується довільне число раз (в залежності скільки разів будуть вводитись нові данні).
4. РЕЗУЛЬТАТИ РОБОТИ ПРОГРАМИ
Після запуску програми з’являється заставка з описом функції програми та іменем розробника (додаток Б). Користувач може зразу ж вийти з програми, натиснувши клавішу Esc. При натисканні клавіші Enter з’являться головне меню програми (додаток В).
Після натиснення клавіші „1” введемо крок обчислення. Далі натиснувши клавішу „2” , з’являються результати роботи програми (додаток Г).
ВИСНОВКИ
У даній роботі розглянуті методи наближеного обчислення таблиці значень функції, яка є розв’язком заданого диф.рівняння на прикладі простого, виправленого і модифікованого методів. Дана методика розрахунку пригідна для розв’язання різних диф.рівнянь першого порядку з початковими умовами. У ході роботи отримані практичні навички програмування на мові Паскаль.
Використані джерела інформації
1. Квєтний Р.Н. Методи комп’ютерних обчислень. – Вінниця: ВДТУ, 2001.
2. Бурківська В.Л., Войцехівський С.О., Гаврилюк І.П. та ін. Методи обчислень. Практикум на ЕОМ. – К.: Вища школа, 1995
3. Каранчук В.П., Сваровський И.Н., Суздальницкий И.Д. Основы применения ЭВМ. – М.: Радио и связь, 1988.
4. Бахвалов Н.С. Численные методы. – М.: Наука, 1975.
5. Волков Е.А. Численные методы. – М.: Наука, 1987.
6. Краскевич В.Е., Зеленский К.Х., Гречко В.И. – К.: Вища школа, 1986
7. Маликов В.Т., Кветный Р.Н. – К.: Вища школа, 1989
|