Лабораторная работа: Анализ накладных расходов

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Кафедра экономико-математических методов и моделей

Лабораторная работа

по эконометрике

Вариант 8

Липецк 2007

Анализ накладных расходов

По данным, представленным в табл. 1, исследуется зависимость между величиной накладных расходов 40 строительных организаций Y (млн. руб.) и следующими тремя основными факторами:

x1 – объемом выполненных работ, млн. руб.

x2 – численностью рабочих, чел.

x3 – фондом зарплаты, млн. руб.

Таблица 1

Задание 1

1. Построить уравнение множественной регрессии в линейной форме с полным набором факторов, отобрать информативные факторы в модель по t-критерию для коэффициентов регрессии.

2. Построить уравнение множественной регрессии только со значимыми факторами, рассчитать индекс корреляции R и оценить качество полученного уравнения регрессии с помощью коэффициента детерминации.

3. Оценить статистическую значимость уравнения регрессии, используя критерий Фишера F(α=0,05) и статистическую значимость параметров регрессии, используя критерий Стьюдента.

4. Дать сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности, β- и ∆-коэффициентов.

5. Проверить выполнение предпосылок МНК, в том числе провести тестирование ошибок уравнения регрессии на гетероскедастичность.

Задание 1

С помощью инструмента Регрессия (Анализ данных в Excel) построим уравнение множественной регрессии в линейной форме с полным набором факторов:

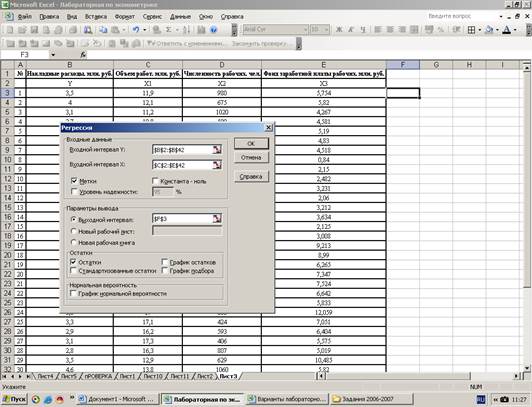
Результат регрессионного анализа содержится в таблицах 2 – 4:

Таблица 2

Таблица 3. Дисперсионный анализ

Таблица 4

Уравнение регрессии выглядит следующим образом:

y= 1,132+ 0,060x₁ + 0,001x₂ +0,103x₃ .

Для отбора информативных факторов в модель воспользуемся инструментом Корреляция (Excel).

Получим

Анализ матрицы коэффициентов парной корреляции показывает, что накладные расходы имеют тесную связь с фондом заработной платы (r_{yx 3} =0,815), с объемом работ и с численностью рабочих. Однако факторы X₁ и X₃ тесно связаны между собой (r_{yx 1 x3} =0,825), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели X₁ – объем работ.

Задание 2

С помощью инструмента Регрессия (Анализ данных в Excel) построим уравнение множественной регрессии только со значимыми факторами. Результат регрессионного анализа содержится в таблицах 5 – 8:

Таблица 5. Регрессионная статистика

Таблица 6. Дисперсионный анализ

Таблица 7

Таблица 8. ВЫВОД ОСТАТКА

Уравнение регрессии имеет вид: y= 1,165+ 0,097x₁ +0,001x₂ . Индекс корреляции (R)=0,851 (табл.5). Коэффициент детерминации = 0,724. Следовательно, около 72% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Задание 3

Проверку значимости уравнения регрессии произведем на основе критерия Фишера. Значение F-критерия Фишера находится в таблице 6 и равен 48,636. Табличное значение при α=0,05 и k₁ =2, k₂ =37 составляет 3,252. Поскольку F_рас › F_табл , то уравнение регрессии следует признать адекватным.

Значимость коэффициентов уравнения регрессии оценим с использованием t-критерия Стьюдента. Расчетные значения для a₁ и a₂ приведены в таблице 7 и равны 4,883 и 2,848. Табличное значение найдем с помощью функции СТЬЮДРАСПОБР при α=0,05 и k=37. Оно составляет 2,026. Т.к. расчетные значения больше табличного, то коэффициенты уравнения регрессии значимы.

Задание 4

Коэффициент эластичности рассчитывается по формуле:

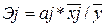
β_j =

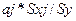
∆_j =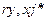β_j /R²

Таблица 9

Тогда Э₁ (для X₁ )=0,097*11,86/2,95=0,391

β₁ =0,097*5,43/0,82=0,581

∆₁ =0,806*0,581/0,724=0,647.

При изменении объема работ на 1% накладные расходы изменятся на 39%.При увеличении объема работ на 5,43 млн. руб. накладные расходы увеличатся на 476 тыс. руб. (0,581*0,82). Доля влияния объема работ в суммарном влиянии всех факторов составляет 64,7%.

Таблица 10

Тогда Э₂ =0,001*568,725/2,95=0,214

β₂ =0,001*276,6/0,82=0,339

∆₂ =0,744*0,339/0,724=0,348.

При изменении численности рабочих на 1% накладные расходы изменятся на 21%. При увеличении численности рабочих на 277 человек накладные расходы увеличатся на 280 тыс. руб. (276,6*0,82). Доля влияния численности рабочих в суммарном влиянии всех факторов составляет 35%.

Задание 5

Проверим выполнение предпосылок МНК:

· Отсутствие автокорреляции

Отсутствие автокорреляции проверяется по d-критерию Дарбина - Уотсона:

.

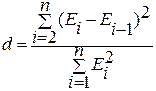d=1,46 (d₁ =1,45 и d₂ =1,59).

Следовательно возникает неопределенность,

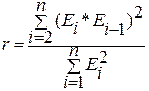
r=0,73 (r_табл =0,851), следовательно автокорреляция отсутствует.

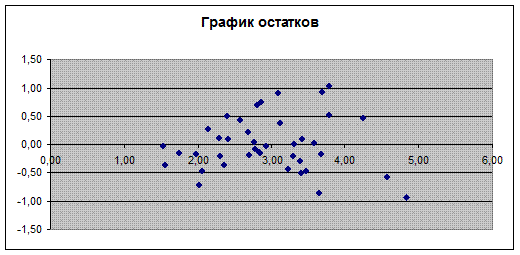
· Случайный характер остатков.

Случайный характер остатков проверяется по графику. Как видно из графика в расположении точек E_i нет направленности, следовательно, E_i – случайные величины и применение МНК оправдано.

· Средняя величина остатков или математическое ожидание равно нулю.

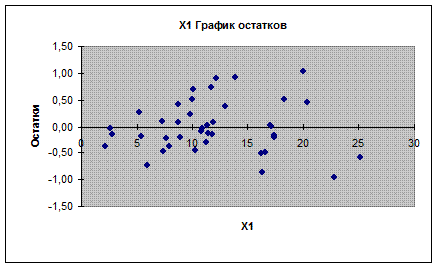
Так как расположение остатков на графике не имеет направленности, то они независимы от значений фактора x₁ .

· Остатки подчиняются нормальному закону распределения.

· Проверка гомоскедастичности остатков:

Гомоскедастичность остатков проверяется по тесту Голдфельда - Кванта.

1) Ранжируем наблюдение в порядке возрастания х. Делим их на две группы: с большим и меньшим x и для каждой группы определяем уравнение регрессии.

Получаем следующие уравнения y=0,84+0,16x₁ + 0,0006x₂ и y=1,996+0,05x₁ + 0,001x₂

Рассчитываем остаточные суммы квадратов для каждой регрессии.

,

.

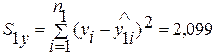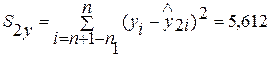Вычисляются F- распределения.

Fнабл.=S_2ŷ /S_1ŷ или Fнабл.= S_1ŷ /S_2ŷ из условий, что в числителе должна быть большая сумма квадратов.

Fнабл. = S_2ŷ /S_1ŷ =2,67

Производится сравнение Fнабл. и Fтабл.

2,06<2,67(при k₁ =40, k₂ =18, α=0,05) следовательно, гетероскедастичность имеет место.