| Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ
5.1. Понятие о средней величине
Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.
Средняя арифметическая
– частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.
Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х
1
, х
2
, ¼, хп
и рассчитывается по формуле
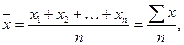
где n
– число вариант;
х
– значение признака.
Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
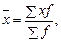
где х
– значение признака;
f
– частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическая имеет следующие свойства:
· произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;
· если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число;
· если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во столько же раз;
· если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится;
· сумма отклонений вариант от их средней арифметической величины равна нулю.
Средняя гармоническая
– это величина, обратная средней арифметической из обратных значений признака. Данный показатель применяется тогда, когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака. Средняя гармоническая также может быть простой и взвешенной.
Средняя гармоническая простая исчисляется по формуле

Средняя гармоническая взвешенная рассчитывается по следующей формуле:
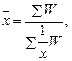
где W = xf
– вес средней гармонической.
Средняя квадратиче
ская
(и т. д. для любой степени) рассчитывается по следующим формулам:
· простая: 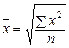
· взвешенная: 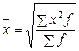
Средняя геометрическая
определяется по следующим формулам:
Реклама

· простая: 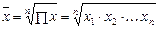 , ,
где Π – знак перемножения.
· взвешенная: 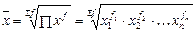 . .
Пример 1
. Имеются следующие данные о размере торговой площади магазинов, входящих в районное потребительское общество (табл. 9).
Таблица 9
| Магазин
|
1-й
|
2-й
|
3-й
|
4-й
|
5-й
|
6-й
|
7-й
|
8-й
|
9-й
|
10-й
|
| Площадь магазина, м2
|
60
|
100
|
80
|
60
|
60
|
80
|
80
|
80
|
100
|
100
|
Необходимо определить среднюю площадь магазина.
Решение
Так как известна площадь каждого магазина, то для вычисления средней площади магазина 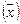 следует применить среднюю арифметическую простую: следует применить среднюю арифметическую простую:
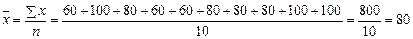 м2
. м2
.
Средняя площадь магазина составляет 80 м2
.
Пример 2
. Приведенные данные в предыдущем примере могут быть представлены в сгруппированном виде (табл. 10).
| Площадь магазинов, м2
(признак – х
)
|
60
|
80
|
100
|
| Число магазинов (частота – f
)
|
3
|
4
|
3
|
Необходимо определить среднюю площадь магазина.
Решение
Если известны отдельные значения признака и соответствующие ему частоты, то применяется средняя арифметическая взвешенная:
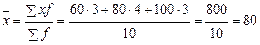 м2
. м2
.
Средняя площадь магазина составляет 80 м2
.
Пример 3
. Имеются следующие данные о распределении магазинов по торговой площади (табл. 11).
Таблица 11
| Группировка магазинов по торговой площади,
м2
(признак – х
)
|
Удельный вес магазинов
в общей численности, % (частость – f
)
|
| 40–60
|
20
|
| 60–80
|
50
|
| 80–100
|
30
|
| Итого
|
100
|
Следует определить среднюю площадь магазина.
Решение
Известны отдельные значения признака и их частоты, следовательно, следует применять среднюю арифметическую взвешенную:
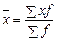 . .
Так как варианты представлены в виде интервального ряда распределения, то, чтобы воспользоваться указанной формулой, необходимо выразить их одним числом, т. е. следует перейти к дискретному ряду распределения (в этом случае находят середину каждого интервала).
Для первого интервала 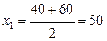 м2
и т. д. по остальным интервалам. Расчеты следует производить в табл. 12. м2
и т. д. по остальным интервалам. Расчеты следует производить в табл. 12.
Таблица 12
| Группировка магазинов
по торговой площади, м2
(х
)
|
Удельный вес магазинов
в общей численности, % ( f
)
|
Середина
интервала (х
)
|
xf
|
| 40–60
|
20
|
50
|
1000
|
| 60–80
|
50
|
70
|
3500
|
| 80–100
|
30
|
90
|
2700
|
| Итого
|
100
|
–
|
7200
|
Таким образом, 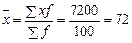 м2
. м2
.
Средняя площадь магазина равна 72 м2
.
Пример 4
. Имеются следующие данные о распределении магазинов по площади (табл. 13).
Таблица 13
| Площадь магазинов,
м2
(признак – х
)
|
Общая площадь магазинов,
входящих в данную группу, м2
(w
= xf
)
|
| 60
|
180
|
| 80
|
320
|
| 100
|
300
|
| Итого
|
800
|
Необходимо определить среднюю площадь магазина.
Решение
Так как весами является площадь W
= xf
, то следует применять среднюю гармоническую взвешенную:
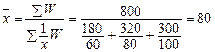 м2
. м2
.
Таким образом, средняя площадь магазина равна 80 м2
.
Реклама

5.2. Вычисление средней из вариационного ряда
«способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
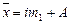 , ,
где i
– размер интервала;
m
1
– момент первого порядка (средняя арифметическая из новых упрощенных вариант 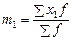 ; ; 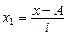 – новые упрощенные варианты; f
– частота); – новые упрощенные варианты; f
– частота);
А
– постоянное число (лучше всего взять его равным варианте, у которой наибольшая частота).
Определим среднее значение признака «способом моментов» на следующем примере.
Пример 5
. Имеются следующие данные о распределении магазинов облпотребсоюза по торговой площади (табл. 14).
Таблица 14
| Группировка магазинов
по торговой площади, м2
(х
)
|
Удельный вес магазинов,
% ( f
)
|
| До 40
|
5
|
| 40–60
|
30
|
| 60–80
|
40
|
| 80–100
|
20
|
| Свыше 100
|
5
|
| Итого
|
100
|
Следует определить среднюю площадь магазинов, применив «способ моментов».
Решение
Данные распределения магазинов по торговой площади представлены в виде интервального ряда распределения с равными интервалами (i
= 20 м2
), следовательно, расчет средней площади магазина можно провести по формуле 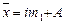 , применив «способ моментов». , применив «способ моментов».
Первый и последний интервалы даны открытыми, т. е. не имеют границ нижней и верхней соответственно. Для определения среднего значения в них границы интервалов следует закрыть. Для первой группы с размером площади до 40 м2
условно считаем, что интервал также равен 20 м2
, затем вычитаем 20 м2
из 40 м2
и находим условную нижнюю границу первого интервала (20 – 40). Условную верхнюю границу последнего интервала определяем аналогично (100 – 120).
Расчеты следует проводить в табл. 15.
Таблица 15
| Группировка мага-
зинов по торговой
площади, м2
(х
)
|
Удельный вес
магазинов, % (f
)
|
Середина
интервала (х
)
|
х
– А
|
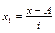
|
xf
|
| 20–40
|
5
|
30
|
–40
|
–2
|
–10
|
| 40–80
|
30
|
50
|
–20
|
–1
|
–30
|
| 60–80
|
40
|
70
|
0
|
0
|
0
|
| 80–100
|
20
|
90
|
20
|
1
|
20
|
| 100–120
|
5
|
110
|
40
|
2
|
10
|
| Итого
|
100
|
–
|
–
|
–
|
–10
|
Наибольшая частота f
равна 40, следовательно, в качестве постоянной величины А
принимаем 70.
Определяем момент первого порядка: 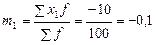 . .
Среднее значение признака равно: 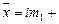 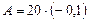 + 70 = + 70 =
= 68 м2
.
Следовательно, средняя площадь магазина составляет 68 м2
.
5.3. Структурные средние
В качестве структурных средних чаще всего используют показатели моды и медианы. Мода
(Мо
) – наиболее часто повторяющееся значение признака. Медиана
(Ме
) – величина признака, которая делит упорядоченный ряд на две равные по численности части.
Если расчет моды и медианы проводится в дискретном ряду, то он опирается на их понятия. В интервальном ряду распределения для расчета моды и медианы применяют следующие формулы.
Мода рассчитывается по формуле
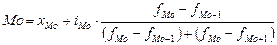 , ,
где хМо
– нижнее значение модального интервала;
iМо
– размер модального интервала;
fМо
– частота модального интервала;
fМо
–1
– частота, предшествующая модальной частоте;
fМо
+1
– частота, последующая за модальной частотой.
Модальному интервалу соответствует наибольшая (модальная) частота. Медиана рассчитывается по формуле
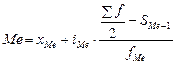 , ,
где хМе
– нижнее значение медианного интервала;
iМе
– размер медианного интервала;
Sf
– сумма частот;
SМе
–1
– сумма частот, предшествующих медианной частоте;
fМе
– медианная частота.
Медианному интервалу соответствует медианная частота. Таким интервалом будет интервал, сумма накопленных частот которого равна или превышает половину суммы всех частот.
Рассмотрим определение моды и медианы на следующих примерах.
Пример 6
. В результате статистического обследования области получены следующие данные по распределению семей по числу детей (табл. 16).
Таблица 16
| Число детей (х
)
|
Количество семей, в % к итогу ( f
)
|
| 0
|
5
|
| 1
|
32
|
| 2
|
34
|
| 3
|
16
|
| 4
|
6
|
| 5
|
4
|
| 6 и более
|
3
|
| Итого
|
100
|
Следует определить моду и медиану.
Решение
В дискретных рядах модой является варианта с наибольшей частотой. Наибольшая частота – 34, следовательно мода равна 2.
Для вычисления медианы определим сумму частот ряда (Sf
= 100), затем рассчитаем полусумму 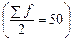 . .
Так как сумма накопленных частот 5 + 32 + 34 = 71 превышает полусумму (71 > 50), то варианта, имеющая значение 2 и соответствующая этой накопленной сумме частот, и есть медиана.
Пример 7
. В результате статистического обследования получены следующие данные распределения продавцов магазинов облпотребсоюза по возрасту (табл. 17).
Таблица 17
| Группировка продавцов по возрасту, лет (х
)
|
Удельный вес продавцов, % ( f
)
|
| До 20
|
6
|
| 20–30
|
24
|
| 30–40
|
35
|
| Окончание табл. 17
|
| Группировка продавцов по возрасту, лет (х
)
|
Удельный вес продавцов, % ( f
)
|
| 40–50
|
26
|
| Свыше 50
|
9
|
| Итого
|
100
|
Необходимо определить моду и медиану.
Решение
В интервальных рядах мода и медиана определяются по вышеприведенным формулам.
Сначала определим модальный интервал, он соответствует наибольшей частоте. Так как наибольшая частота равна 35 и является модальной, то интервал 30–40 является модальным интервалом. Затем подставим данные в следующую формулу:
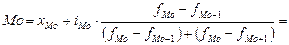
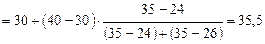 лет. лет.
Определим медианный интервал. Полусумма частот равна 50 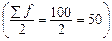 . Накапливая частоты, определим интересующий интервал. Так как сумма накопленных частот 6 + 24 + 35 = 65 превышает полусумму (65 > 50), значит 35 является медианной частотой, а интервал 30–40 является медианным интервалом. . Накапливая частоты, определим интересующий интервал. Так как сумма накопленных частот 6 + 24 + 35 = 65 превышает полусумму (65 > 50), значит 35 является медианной частотой, а интервал 30–40 является медианным интервалом.
Затем подставим данные в формулу
 . .
Таким образом, мода равна 35,5 лет (больше всего продавцов
в возрасте 35,5 лет), медиана – 35,7 лет (50 % продавцов достигли возраста 35,7 лет).
|