Национальный Горный Университет Украины
Контрольная работа
по дисциплине
«Использование вычислительной техники»
Днепропетровск
Используя приложение Excel пакета MicrosoftOffice (версии 95,97, 2000 или XP) рассчитать значения функций и построить графики.
Оформить работу в текстовом редакторе MicrosoftWord (все выражения должны быть набраны в редакторе формул MicrosoftEquation).
Задание 1. Исследовать методами математического анализа поведение функций при заданных значениях аргумента
Алгебраические рациональные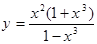
1. Область существования: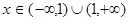
2. Четность: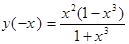 функция ни четная, ни нечетная функция ни четная, ни нечетная
3. Точки разрыва: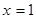 .Промежутки непрерывности .Промежутки непрерывности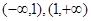
4. Точки пересечения функции с осями координат: (-1,0),(0,0).
5. Экстремум функции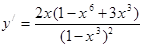 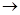 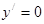 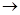 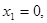 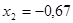 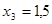
| x |
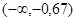 |
-0,67 |
(-0,67; 0) |
0 |
(0,1) |
(1;1,5) |
1,5 |
(1,5;+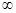 ) ) |
| y/
|
+ |
0 |
– |
0 |
+ |
+ |
0 |
– |
| y |
возрастает |
0,23 |
убывает |
0 |
возрастает |
возрастает |
-4,14 |
убывает |
6. Вертикальная асимптота 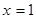
Значения функции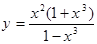
| x |
y |
x |
y |
| -3 |
-8,35714 |
0,1 |
0,01002 |
| -2,9 |
-7,74751 |
0,2 |
0,040645 |
| -2,8 |
-7,15684 |
0,3 |
0,094995 |
| -2,7 |
-6,58507 |
0,4 |
0,18188 |
| -2,6 |
-6,03218 |
0,5 |
0,321429 |
| -2,5 |
-5,49812 |
0,6 |
0,558367 |
| -2,4 |
-4,98288 |
0,7 |
1,001629 |
| -2,3 |
-4,48648 |
0,8 |
1,982951 |
| -2,2 |
-4,00896 |
0,9 |
5,16786 |
| -2,1 |
-3,55043 |
1 |
| -2 |
-3,11111 |
1,1 |
-8,52118 |
| -1,9 |
-2,69131 |
1,2 |
-5,39604 |
| -1,8 |
-2,29152 |
1,3 |
-4,51373 |
| -1,7 |
-1,91249 |
1,4 |
-4,20771 |
| -1,6 |
-1,55529 |
1,5 |
-4,14474 |
| -1,5 |
-1,22143 |
1,6 |
-4,21375 |
| -1,4 |
-0,91299 |
1,7 |
-4,36713 |
| -1,3 |
-0,63276 |
1,8 |
-4,58106 |
| -1,2 |
-0,38428 |
1,9 |
-4,84229 |
| -1,1 |
-0,17182 |
2 |
-5,14286 |
| -1 |
0 |
2,1 |
-5,47767 |
| -0,9 |
0,126958 |
2,2 |
-5,84332 |
| -0,8 |
0,206561 |
2,3 |
-6,23743 |
| -0,7 |
0,23971 |
2,4 |
-6,65832 |
| -0,6 |
0,232105 |
2,5 |
-7,1047 |
| -0,5 |
0,194444 |
2,6 |
-7,57564 |
| -0,4 |
0,140752 |
2,7 |
-8,07039 |
| -0,3 |
0,085268 |
2,8 |
-8,58838 |
| -0,2 |
0,039365 |
2,9 |
-9,12914 |
| -0,1 |
0,00998 |
3 |
-9,69231 |
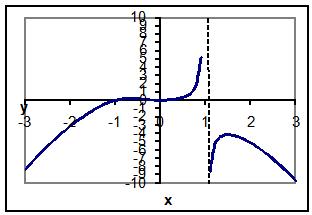
График функции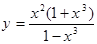
Алгебраические иррациональные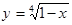
1. Область существования:
2. Четность: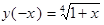 функция ни четная, ни нечетная функция ни четная, ни нечетная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 1),(1,0).
5. Экстремум функции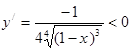 , следовательно, функция y(x) убывает , следовательно, функция y(x) убывает
6. Выпуклость, вогнутость функции:
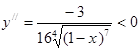 , следовательно, кривая выпукла , следовательно, кривая выпукла
Значения функции 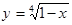
| x |
y |
x |
y |
| -3 |
1,414214 |
-1 |
1,189207 |
| -2,9 |
1,405291 |
-0,9 |
1,174055 |
| -2,8 |
1,396194 |
-0,8 |
1,158292 |
| -2,7 |
1,386917 |
-0,7 |
1,141858 |
| -2,6 |
1,377449 |
-0,6 |
1,124683 |
| -2,5 |
1,367782 |
-0,5 |
1,106682 |
| -2,4 |
1,357906 |
-0,4 |
1,087757 |
| -2,3 |
1,347809 |
-0,3 |
1,06779 |
| -2,2 |
1,337481 |
-0,2 |
1,046635 |
| -2,1 |
1,326907 |
-0,1 |
1,024114 |
| -2 |
1,316074 |
0 |
1 |
| -1,9 |
1,304967 |
0,1 |
0,974004 |
| -1,8 |
1,293569 |
0,2 |
0,945742 |
| -1,7 |
1,281861 |
0,3 |
0,914691 |
| -1,6 |
1,269823 |
0,4 |
0,880112 |
| -1,5 |
1,257433 |
0,5 |
0,840896 |
| -1,4 |
1,244666 |
0,6 |
0,795271 |
| -1,3 |
1,231493 |
0,7 |
0,740083 |
| -1,2 |
1,217883 |
0,8 |
0,66874 |
| -1,1 |
1,203801 |
0,9 |
0,562341 |
| -1 |
1,189207 |
1 |
0 |
График функции
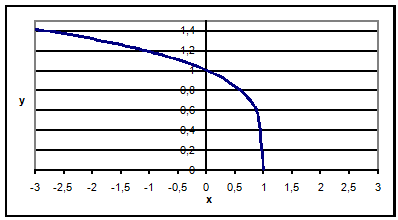
Тригонометрические:функция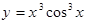
1. Область существования: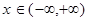
2. Четность: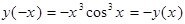 функция нечетная функция нечетная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 0),(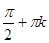 ,0), ,0), 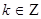
5. Экстремум функции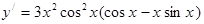 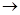 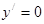 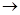 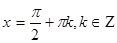 , , 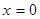
Значения функции 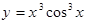
| x |
y |
x |
y |
x |
y |
x |
y |
| -31,4 |
-30947,4 |
-17,27 |
0 |
3,14 |
-30,959 |
17,27 |
-0,00346 |
| -30,615 |
-9676,29 |
-16,485 |
1623,773 |
3,925 |
-21,5061 |
18,055 |
2023,979 |
| -29,83 |
0,091927 |
-15,7 |
3869,525 |
4,71 |
0 |
18,84 |
6686,259 |
| -29,045 |
9048,639 |
-14,915 |
1146,551 |
5,495 |
58,17235 |
19,625 |
2752,484 |
| -28,26 |
22562,26 |
-14,13 |
0 |
6,28 |
247,6694 |
20,41 |
0,009432 |
| -27,475 |
7028,394 |
-13,345 |
-857,374 |
7,065 |
126,0212 |
21,195 |
-3258,35 |
| -26,69 |
0 |
-12,56 |
-1981,26 |
7,85 |
0 |
21,98 |
-10617 |
| -25,905 |
-6390,02 |
-11,775 |
-566,904 |
8,635 |
-224,652 |
22,765 |
-4316,48 |
| -25,12 |
-15847,2 |
-10,99 |
0 |
9,42 |
-835,868 |
23,55 |
-0,02226 |
| -24,335 |
-4907,58 |
-10,205 |
381,5954 |
10,205 |
-381,595 |
24,335 |
4907,579 |
| -23,55 |
0 |
-9,42 |
835,8683 |
10,99 |
-0,00023 |
25,12 |
15847,22 |
| -22,765 |
4316,479 |
-8,635 |
224,6522 |
11,775 |
566,9042 |
25,905 |
6390,015 |
| -21,98 |
10617,01 |
-7,85 |
0 |
12,56 |
1981,265 |
26,69 |
0,047166 |
| -21,195 |
3258,345 |
-7,065 |
-126,021 |
13,345 |
857,3739 |
27,475 |
-7028,39 |
| -20,41 |
0 |
0 |
0 |
14,13 |
0,001039 |
28,26 |
-22562,3 |
| -19,625 |
-2752,48 |
0,785 |
0,171231 |
14,915 |
-1146,55 |
29,045 |
-9048,64 |
| -18,84 |
-6686,26 |
1,57 |
0 |
15,7 |
-3869,52 |
29,83 |
-0,09193 |
| -18,055 |
-2023,98 |
2,355 |
-4,60118 |
16,485 |
-1623,77 |
30,615 |
9676,285 |
| 31,4 |
30947,37 |
График функции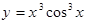
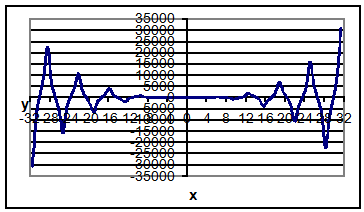
Гиперболические: функция 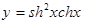
1. Область существования: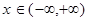
2. Четность: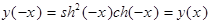 функция четная функция четная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции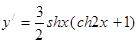 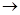 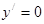 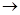 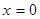
Значения функции 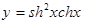
| x |
y |
x |
y |
x |
y |
| -3 |
1010,369 |
-1 |
2,131145 |
1 |
2,131145 |
| -2,9 |
748,0854 |
-0,9 |
1,510096 |
1,1 |
2,976561 |
| -2,8 |
553,8202 |
-0,8 |
1,054878 |
1,2 |
4,125531 |
| -2,7 |
409,9402 |
-0,7 |
0,722286 |
1,3 |
5,685108 |
| -2,6 |
303,383 |
-0,6 |
0,480502 |
1,4 |
7,799941 |
| -2,5 |
224,4723 |
-0,5 |
0,306196 |
1,5 |
10,66543 |
| -2,4 |
166,0397 |
-0,4 |
0,182396 |
1,6 |
14,54546 |
| -2,3 |
122,7752 |
-0,3 |
0,096937 |
1,7 |
19,79642 |
| -2,2 |
90,74509 |
-0,2 |
0,04135 |
1,8 |
26,8995 |
| -2,1 |
67,03564 |
-0,1 |
0,010084 |
1,9 |
36,50441 |
| -2 |
49,48836 |
0 |
0 |
2 |
49,48836 |
| -1,9 |
36,50441 |
0,1 |
0,010084 |
2,1 |
67,03564 |
| -1,8 |
26,8995 |
0,2 |
0,04135 |
2,2 |
90,74509 |
| -1,7 |
19,79642 |
0,3 |
0,096937 |
2,3 |
122,7752 |
| -1,6 |
14,54546 |
0,4 |
0,182396 |
2,4 |
166,0397 |
| -1,5 |
10,66543 |
0,5 |
0,306196 |
2,5 |
224,4723 |
| -1,4 |
7,799941 |
0,6 |
0,480502 |
2,6 |
303,383 |
| -1,3 |
5,685108 |
0,7 |
0,722286 |
2,7 |
409,9402 |
| -1,2 |
4,125531 |
0,8 |
1,054878 |
2,8 |
553,8202 |
| -1,1 |
2,976561 |
0,9 |
1,510096 |
2,9 |
748,0854 |
| -1 |
2,131145 |
1 |
2,131145 |
3 |
1010,369 |
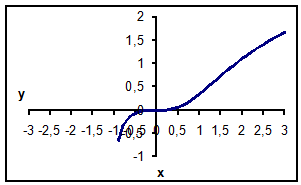
График функции
Натуральные логарифмы:функция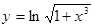
1. Область существования: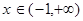
2. Четность: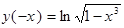 функция ни четная, ни нечетная функция ни четная, ни нечетная
3. Функция непрерывна.4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции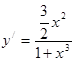 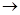 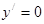 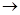 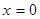
6. Точки перегиба: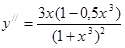 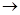 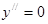 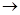 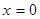 , , 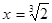
Значения функции 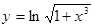
| x |
y |
x |
y |
| -1 |
1 |
0,346574 |
| -0,9 |
-0,65282 |
1,1 |
0,423149 |
| -0,8 |
-0,35872 |
1,2 |
0,501784 |
| -0,7 |
-0,21004 |
1,3 |
0,581106 |
| -0,6 |
-0,12167 |
1,4 |
0,660077 |
| -0,5 |
-0,06677 |
1,5 |
0,737953 |
| -0,4 |
-0,03307 |
1,6 |
0,814228 |
| -0,3 |
-0,01369 |
1,7 |
0,888577 |
| -0,2 |
-0,00402 |
1,8 |
0,960809 |
| -0,1 |
-0,0005 |
1,9 |
1,03083 |
| 0 |
0 |
2 |
1,098612 |
| 0,1 |
0,0005 |
2,1 |
1,164175 |
| 0,2 |
0,003984 |
2,2 |
1,227567 |
| 0,3 |
0,013321 |
2,3 |
1,288857 |
| 0,4 |
0,031018 |
2,4 |
1,348124 |
| 0,5 |
0,058892 |
2,5 |
1,405454 |
| 0,6 |
0,097783 |
2,6 |
1,460935 |
| 0,7 |
0,147453 |
2,7 |
1,514656 |
| 0,8 |
0,206717 |
2,8 |
1,566703 |
| 0,9 |
0,273772 |
2,9 |
1,617158 |
| 1 |
0,346574 |
3 |
1,666102 |
Сочетание тригонометрических, гиперболических:функция 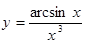
1. Область существования: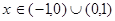 .Точка разрыва .Точка разрыва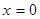 . .
2. Четность: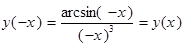 функция четная. функция четная.
4. Точек пересечения функции с осями координат нет.
5. Экстремум функции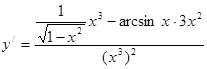
Значения функции 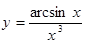
| x |
y |
| -1 |
1,570796 |
| -0,9 |
1,536035 |
| -0,8 |
1,811123 |
| -0,7 |
2,260634 |
| -0,6 |
2,979172 |
| -0,5 |
4,18879 |
| -0,4 |
6,429951 |
| -0,3 |
11,28491 |
| -0,2 |
25,16974 |
| -0,1 |
100,1674 |
| 0 |
| 0,1 |
100,1674 |
| 0,2 |
25,16974 |
| 0,3 |
11,28491 |
| 0,4 |
6,429951 |
| 0,5 |
4,18879 |
| 0,6 |
2,979172 |
| 0,7 |
2,260634 |
| 0,8 |
1,811123 |
| 0,9 |
1,536035 |
| 1 |
1,570796 |
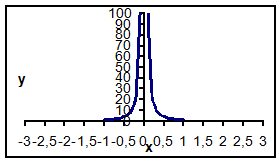
Задание 2. Выполнить исследование методами математического анализа уравнения функции
и определить значения аргумента и параметра (если он имеется). Вид уравнения выбирается самостоятельно
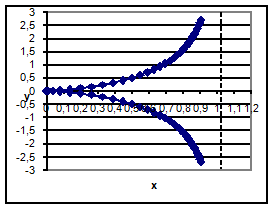
Циссоида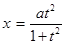 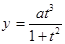 ( (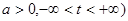
Обе функции 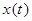 и и 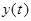 определены при всех значениях определены при всех значениях 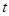 . Заметим, что . Заметим, что 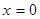 , , 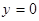 при при 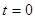 . Найдем производные . Найдем производные 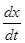 и и 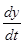 : :
Реклама

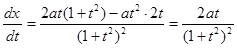
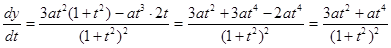
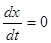 при при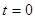 , ,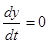 при при 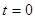 . .
Для параметра t получили критическую точку 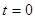 . .
Далее, находим
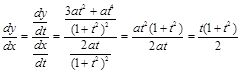
Составляем таблицу:
Найдем 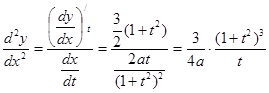
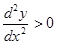 при при 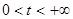 - кривая вогнута; - кривая вогнута;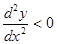 при при 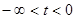 - кривая выпукла - кривая выпукла
Точка 0 – точка возврата (такая точка, где направление движения вдоль кривой скачкообразно меняется на противоположное).
Вертикальная асимптота: 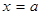 . .
Значения функции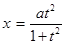 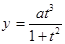 (при (при 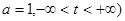
| t |
x |
y |
| -3 |
0,9 |
-2,7 |
| -2,9 |
0,89373 |
-2,59182 |
| -2,8 |
0,886878 |
-2,48326 |
| -2,7 |
0,879373 |
-2,37431 |
| -2,6 |
0,871134 |
-2,26495 |
| -2,5 |
0,862069 |
-2,15517 |
| -2,4 |
0,852071 |
-2,04497 |
| -2,3 |
0,841017 |
-1,93434 |
| -2,2 |
0,828767 |
-1,82329 |
| -2,1 |
0,815157 |
-1,71183 |
| -2 |
0,8 |
-1,6 |
| -1,9 |
0,78308 |
-1,48785 |
| -1,8 |
0,764151 |
-1,37547 |
| -1,7 |
0,742931 |
-1,26298 |
| -1,6 |
0,719101 |
-1,15056 |
| -1,5 |
0,692308 |
-1,03846 |
| -1,4 |
0,662162 |
-0,92703 |
| -1,3 |
0,628253 |
-0,81673 |
| -1,2 |
0,590164 |
-0,7082 |
| -1,1 |
0,547511 |
-0,60226 |
| -1 |
0,5 |
-0,5 |
| -0,9 |
0,447514 |
-0,40276 |
| -0,8 |
0,390244 |
-0,3122 |
| -0,7 |
0,328859 |
-0,2302 |
| -0,6 |
0,264706 |
-0,15882 |
| -0,5 |
0,2 |
-0,1 |
| -0,4 |
0,137931 |
-0,05517 |
| -0,3 |
0,082569 |
-0,02477 |
| -0,2 |
0,038462 |
-0,00769 |
| -0,1 |
0,009901 |
-0,00099 |
| 0 |
0 |
0 |
| 0,1 |
0,009901 |
0,00099 |
| 0,2 |
0,038462 |
0,007692 |
| 0,3 |
0,082569 |
0,024771 |
| 0,4 |
0,137931 |
0,055172 |
| 0,5 |
0,2 |
0,1 |
| 0,6 |
0,264706 |
0,158824 |
| 0,7 |
0,328859 |
0,230201 |
| 0,8 |
0,390244 |
0,312195 |
| 0,9 |
0,447514 |
0,402762 |
| 1 |
0,5 |
0,5 |
| 1,1 |
0,547511 |
0,602262 |
| 1,2 |
0,590164 |
0,708197 |
| 1,3 |
0,628253 |
0,816729 |
| 1,4 |
0,662162 |
0,927027 |
| 1,5 |
0,692308 |
1,038462 |
| 1,6 |
0,719101 |
1,150562 |
| 1,7 |
0,742931 |
1,262982 |
| 1,8 |
0,764151 |
1,375472 |
| 1,9 |
0,78308 |
1,487852 |
| 2 |
0,8 |
1,6 |
| 2,1 |
0,815157 |
1,71183 |
| 2,2 |
0,828767 |
1,823288 |
| 2,3 |
0,841017 |
1,93434 |
| 2,4 |
0,852071 |
2,04497 |
| 2,5 |
0,862069 |
2,155172 |
| 2,6 |
0,871134 |
2,264948 |
| 2,7 |
0,879373 |
2,374306 |
| 2,8 |
0,886878 |
2,483258 |
| 2,9 |
0,89373 |
2,591817 |
| 3 |
0,9 |
2,7 |
График функции
Список использованной литературы
1. Гай Харт-Девис WORD 2000. Базовый курс: Пер. с англ. – К.:ВЕК+,М:ЭНТРОП, СПБ: Корона-Принт, 2000. – 400 с., ил.
2. Джен Вейсскопф EXCEL 2000. Базовый курс (русифицированная версия): пер. с англ. – К.:ВЕК+, М.:ЭНТРОП, СПБ.: Корона-Принт, 2000. – 400 с., ил.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления , том 1: учебное пособие для втузов. – 13-е изд. – М.: Наука, 1985. – 432 с.
4. Выгодский М.Я. Справочник по высшей математике. – М.:Физматгиз, 1963– 872с.
|