
Единый государственный экзамен по
МАТЕМАТИКЕ
Демонстрационный вариант
контрольных измерительных материалов единого
государственного экзамена 2012 года
по
математике
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
Пояснения к демонстрационному варианту
контрольных измерительных материалов для ЕГЭ 2012 года
по МАТЕМАТИКЕ
Демонстрационный вариант ЕГЭ по математике 2012 года разработан по заданию Федеральной службы по надзору в сфере образования и науки Российской Федерации.
Демонстрационный вариант предназначен для того, чтобы дать представление о структуре будущих контрольных измерительных материалов, количестве заданий, их форме, уровне сложности. Задания демонстрационного варианта не отражают всех вопросов содержания, которые могут быть включены в контрольные измерительные материалы в 2012 году. Структура работы приведена в спецификации, а полный перечень вопросов – в кодификаторах требований и элементов содержания по математике для составления контрольных измерительных материалов ЕГЭ 2012 года.
Правильное решение каждого из заданий В1–В14 части 1 экзаменационной работы оценивается 1 баллом. Правильное решение каждого из заданий С1 и С2 оценивается 2 баллами, С3 и С4 – 3 баллами, С5 и С6 – 4 баллами. Максимальный первичный балл за выполнение всей работы – 32.
Верное выполнение не менее пяти заданий экзаменационной работы отвечает минимальному уровню подготовки, подтверждающему освоение выпускником основных общеобразовательных программ общего (полного) среднего образования.
К каждому заданию с развёрнутым ответом, включённому в демонстрационный вариант, даётся возможное решение. Приведённые критерии оценивания позволяют составить представление о требованиях к полноте и правильности решений. Демонстрационный вариант контрольных измерительных материалов, система оценивания, спецификация и кодификаторы помогут выработать стратегию подготовки к ЕГЭ по математике.
Единый государственный экзамен по МАТЕМАТИКЕ
Демонстрационный вариант
контрольных измерительных материалов 2012 года
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике даётся 4 часа (240 мин.). Работа состоит из двух частей и содержит 20 заданий.
Реклама

Часть 1 содержит 14 заданий с кратким ответом (В1–В14) базового уровня по материалу курса математики. Ответом является целое число или конечная десятичная дробь.
Часть 2 содержит 6 более сложных заданий (С1–С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценке работы.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха
!
Часть 1
| Ответом на задания В1–В14 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
|
Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Ярославле по результатам многолетних наблюдений. Найдите по диаграмме количество месяцев, когда средняя температура в Ярославле была отрицательной.
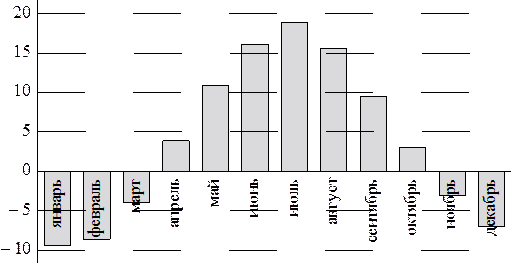
 Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах. Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
Строительная фирма планирует купить 70 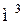 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой? пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
| Поставщик
|
Стоимость
пеноблоков
(руб. за 1 м3
)
|
Стоимость доставки
(руб.)
|
Дополнительные
условия доставки
|
| А |
2 600 |
10 000 |
Нет |
| Б |
2 800 |
8 000 |
При заказе товара на сумму свыше 150 000 рублей доставка бесплатная |
| В |
2 700 |
8 000 |
При заказе товара на сумму свыше 200 000 рублей доставка бесплатная |
Найдите корень уравнения 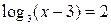 . .
Треугольник 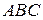 вписан в окружность с центром вписан в окружность с центром 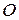 . Найдите угол . Найдите угол 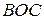 , если угол , если угол 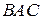 равен равен 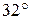 . .
Найдите 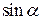 , если , если 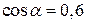 и и 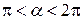 . .
На рисунке изображён график дифференцируемой функции 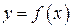 . На оси абсцисс отмечены девять точек: . На оси абсцисс отмечены девять точек: 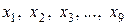 . Среди этих точек найдите все точки, в которых производная функции . Среди этих точек найдите все точки, в которых производная функции 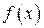 отрицательна. В ответе укажите количество найденных точек. отрицательна. В ответе укажите количество найденных точек.
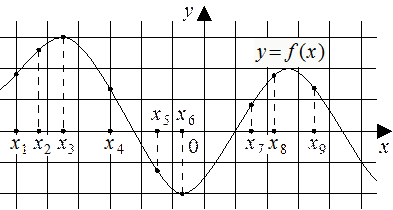
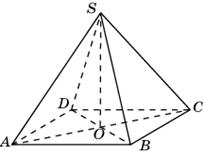 Диагональ Диагональ 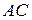 основания правильной четырёхугольной пирамиды основания правильной четырёхугольной пирамиды 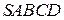 равна 6. Высота пирамиды равна 6. Высота пирамиды 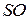 равна 4. Найдите длину бокового ребра равна 4. Найдите длину бокового ребра 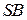 . .
В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Реклама

Объём первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м³).
Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой 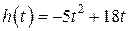 , где , где 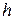 – высота в метрах, – высота в метрах, 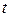 – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров. – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
Весной катер идёт против течения реки в 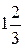 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 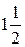 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Найдите наибольшее значение функции
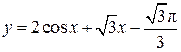 на отрезке на отрезке 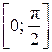 . .
Часть 2
а)
Решите уравнение 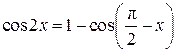 . .
б)
Найдите все корни этого уравнения, принадлежащие промежутку 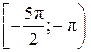 . .
Сторона основания правильной треугольной призмы 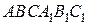 равна равна 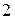 , а диагональ боковой грани равна , а диагональ боковой грани равна 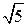 . Найдите угол между плоскостью . Найдите угол между плоскостью 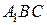 и плоскостью основания призмы. и плоскостью основания призмы.
Решите систему неравенств 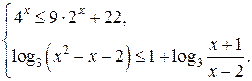
На стороне BA
угла 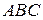 , равного , равного 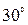 , взята такая точка D
, что , взята такая точка D
, что 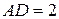 и и 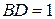 . Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
. . Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
.
Найдите все значения 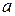 , при каждом из которых наименьшее значение функции , при каждом из которых наименьшее значение функции 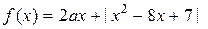 больше 1. больше 1.
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 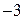 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 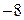 . .
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Система оценивания демонстрационного варианта
контрольных измерительных материалов по МАТЕМАТИКЕ
Ответы к заданиям части 1
Каждое правильно выполненное задание части 1 оценивается 1 баллом. Задания части 1 считаются выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
| Задание
|
Ответ
|
| В1 |
5 |
| В2 |
5 |
| В3 |
18 |
| В4 |
192000 |
| В5 |
12 |
| В6 |
64 |
| В7 |
–0,8 |
| В8 |
3 |
| В9 |
5 |
| В10 |
0,92 |
| В11 |
9 |
| В12 |
2,4 |
| В13 |
5 |
| В14 |
1 |
Ответы к заданиям части 2
Решения и критерии оценивания заданий части 2
Количество баллов, выставляемых за выполнение заданий части 2 зависит от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, в частности, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное число баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.
В критериях оценивания конкретных заданий содержатся общие требования к выставлению баллов.
При выполнении задания можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.
а)
Решите уравнение 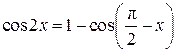 . .
б)
Найдите все корни этого уравнения, принадлежащие промежутку 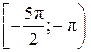 . .
Решение.
а)
Так как 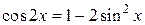 , , 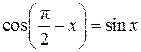 , то , то 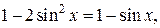 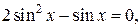 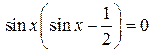 . .
 Корни уравнения: Корни уравнения: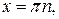 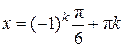 ,
, 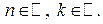
б)
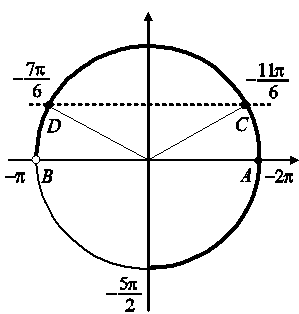
Корни уравнения 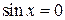 изображаются точками изображаются точками 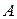 и и 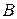 , а корни уравнения , а корни уравнения 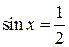 — точками — точками 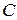 и и 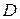 , промежуток , промежуток 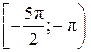 изображается жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: изображается жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: 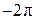 , , 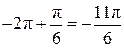 и и 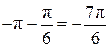 . .
Ответ:
а)
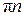 , , 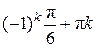 , , 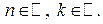
б)
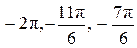 . .
Другие решения пункта б).
б)
Корни, принадлежащие промежутку 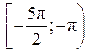 , отберем по графику , отберем по графику 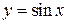 . Прямая . Прямая 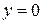 (ось (ось 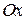 ) пересекает график в единственной точке ) пересекает график в единственной точке 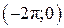 , абсцисса которой принадлежит промежутку , абсцисса которой принадлежит промежутку 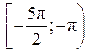 . .
Прямая 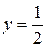 пересекает график ровно в двух точках, абсциссы которых принадлежат пересекает график ровно в двух точках, абсциссы которых принадлежат 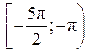 (см. рис.). Так как период функции (см. рис.). Так как период функции 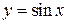 равен равен 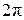 , то эти абсциссы равны, соответственно, , то эти абсциссы равны, соответственно,
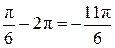 и и 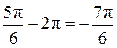 . .
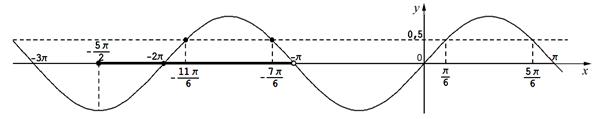
В промежутке 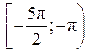 содержатся три корня: содержатся три корня: 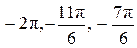 . .
б)
Пусть  . Подставляя . Подставляя 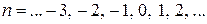 , получаем , получаем 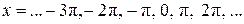 . Промежутку . Промежутку 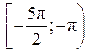 принадлежит только принадлежит только 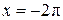 . .
Пусть 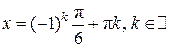 . Подставляя . Подставляя 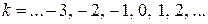 , получаем: , получаем: 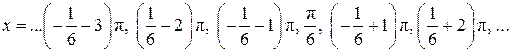 . Промежутку . Промежутку 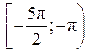 принадлежат только принадлежат только 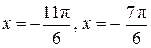 . .
Промежутку 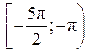 принадлежат корни: принадлежат корни: 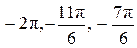 . .
б)
Отберем корни, принадлежащие промежутку 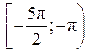 . .
Пусть 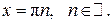 Тогда Тогда 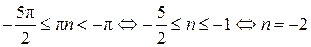 . Корень, принадлежащий промежутку . Корень, принадлежащий промежутку 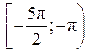 : : 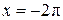 . .
Пусть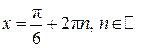 . .
Тогда 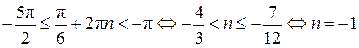 . .
Корень, принадлежащий промежутку 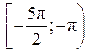 : : 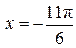 . .
Пусть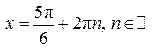 . .
Тогда 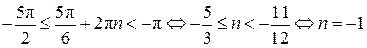 . .
Корень, принадлежащий промежутку 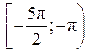 : : 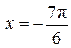 . .
Промежутку 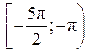 принадлежат корни: принадлежат корни: 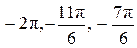 . .
| Содержание критерия |
Баллы |
| Обоснованно получены верные ответы в п. а)
и в п. б)
|
2 |
Обоснованно получен верный ответ в п. а)
, но обоснование отбора корней в п. б)
не приведено или
задача в п. а)
обоснованно сведена к исследованию простейших тригонометрических уравнений без предъявления верного ответа, а в п. б)
приведен обоснованный отбор корней
|
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный балл
|
2 |
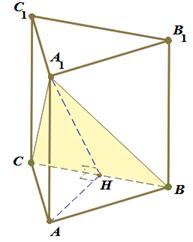
Сторона основания правильной треугольной призмы 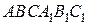 равна равна 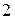 , а диагональ боковой грани равна , а диагональ боковой грани равна 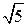 . Найдите угол между плоскостью . Найдите угол между плоскостью 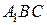 и плоскостью основания призмы. и плоскостью основания призмы.
Решение.
Обозначим 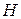 середину ребра середину ребра 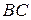 (см. рисунок). Так как треугольник (см. рисунок). Так как треугольник 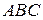 равносторонний, а треугольник равносторонний, а треугольник 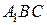 – равнобедренный, отрезки – равнобедренный, отрезки 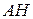 и и 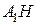 перпендикулярны перпендикулярны 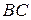 . Следовательно, . Следовательно, 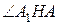 – линейный угол двугранного угла с гранями – линейный угол двугранного угла с гранями 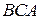 и и 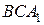 . .
Из треугольника 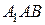 найдём: найдём: 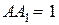 . .
Из треугольника 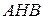 найдём: найдём: 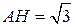 . .
Из треугольника 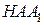 найдём: найдём: 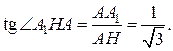
 Искомый угол равен Искомый угол равен  . .
Ответ:
 . .
Возможны другие формы записи ответа.
Например:
А) 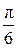 ; ;
Б) 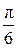 рад. рад.
В)  и т.п. и т.п.
Возможны другие решения.
Например, с использованием векторов или метода координат.
| Содержание критерия |
Баллы |
| Обоснованно получен верный ответ |
2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ, или решение не закончено, или при правильном ответе решение недостаточно обосновано |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный
балл
|
2 |
Решите систему неравенств 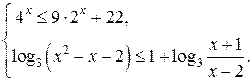
Решение.
1. Неравенство 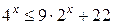 запишем в виде запишем в виде 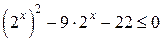 . Относительно . Относительно 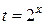 неравенство имеет вид: неравенство имеет вид: 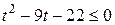 , откуда получаем: , откуда получаем: 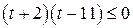 , , 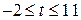 . .
Значит, 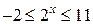 , , 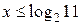 . .
2. Второе неравенство системы определено при 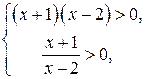
то есть при 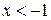 и и  . .
При допустимых значениях переменной получаем: 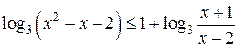 , , 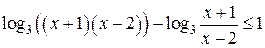 , , 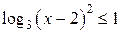 , ,  , , 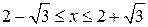 . .
С учётом области допустимых значений переменной получаем решение второго неравенства системы: 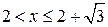 . .
3. Сравним 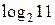 и и 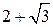 . Так как . Так как 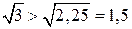 , то , то
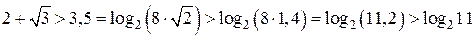 , следовательно, , следовательно, 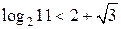 . .
Решение системы неравенств: 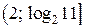 . .
Ответ:
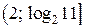 . .
| Содержание критерия |
Баллы |
| Обоснованно получен верный ответ |
3 |
| Для обоих неравенств системы обоснованно получены верные ответы, но не проведено обоснованного сравнения значений конечных точек найденных промежутков |
2 |
| Для одного из двух неравенств системы обоснованно получен верный ответ |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный
балл
|
3 |
Комментарий.
Если обоснованно получены оба ответа: 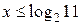 и и 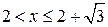 , после чего лишь сказано
, но никак не обосновано, что , после чего лишь сказано
, но никак не обосновано, что 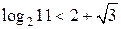 , то такое решение оценивается в 2 балла. , то такое решение оценивается в 2 балла.
На стороне BA
угла 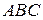 , равного , равного 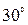 , взята такая точка D
, что , взята такая точка D
, что 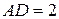 и и 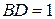 . Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
. . Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
.
Решение.
Центр O
искомой окружности принадлежит серединному перпендикуляру к отрезку AD
. Обозначим P
середину отрезка AD
, Q
– основание перпендикуляра, опущенного из точки O
на прямую BC
,E
–
точку пересечения серединного перпендикуляра с прямой BC
(см. рисунок а). Из условия касания окружности и прямой BC
следует, что отрезки OA
, OD
и OQ
равны радиусу R
окружности.
Заметим, что точка 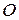 не может лежать по ту же сторону от прямой AB
, что и точка E
, так как в этом случае расстояние от точки O
до прямой BC
меньше, чем расстояние от неё до точки A
. не может лежать по ту же сторону от прямой AB
, что и точка E
, так как в этом случае расстояние от точки O
до прямой BC
меньше, чем расстояние от неё до точки A
.
Из прямоугольного треугольника BPE
с катетом BP
=
2 и 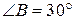 находим, что PE
= находим, что PE
= 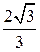 .
.
Так как OA
=
R
и 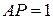 , получаем: , получаем: 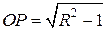 , следовательно, , следовательно, 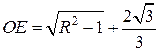 . .
Из прямоугольного треугольника OQE
, в котором 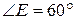 , находим: , находим:
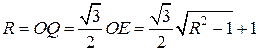 .
.
В результате получаем уравнение:
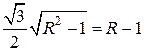 .
.
Возведём в квадрат обе части этого уравнения и приведём подобные члены. Получим уравнение R
2
– 8R +
7 = 0, решая которое находим два корня: R
1
= 1, R
2
= 7. Если радиус равен 1, то центром окружности является точка  (см. рисунок б). (см. рисунок б).
Ответ:
1 или 7.
Другое решение.
Пусть точка 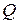 касания окружности с прямой касания окружности с прямой 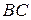 лежит на луче лежит на луче 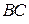 (см. рисунок а). По теореме о касательной и секущей (см. рисунок а). По теореме о касательной и секущей
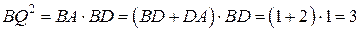 , ,
откуда 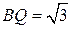 . .
Пусть 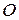 – точка пересечения луча – точка пересечения луча 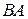 и перпендикуляра к и перпендикуляра к 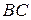 , проведённого через точку , проведённого через точку 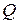 . Из прямоугольного треугольника . Из прямоугольного треугольника 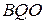 находим: находим:
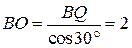 , тогда , тогда 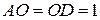 и и 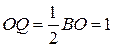 . .
Таким образом, точка 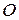 удалена от точек удалена от точек 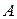 , , 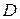 и и 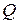 на одно и то же расстояние, равное 1. Следовательно, на одно и то же расстояние, равное 1. Следовательно, 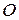 – центр искомой окружности, а её радиус равен 1. – центр искомой окружности, а её радиус равен 1.
Пусть теперь точка 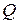 касания окружности с прямой касания окружности с прямой 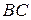 лежит на продолжении лежит на продолжении 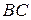 за точку за точку 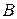 (см. рисунок б), а прямая, проходящая через точку (см. рисунок б), а прямая, проходящая через точку 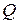 перпендикулярно перпендикулярно 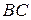 , пересекает прямую , пересекает прямую 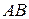 в точке в точке 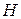 , а окружность вторично – в точке , а окружность вторично – в точке 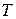 . Тогда . Тогда
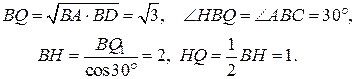
Если 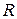 – радиус окружности, то – радиус окружности, то 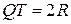 . По теореме о двух секущих . По теореме о двух секущих 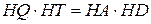 , то есть , то есть 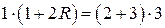 , откуда находим, что , откуда находим, что 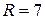 . .
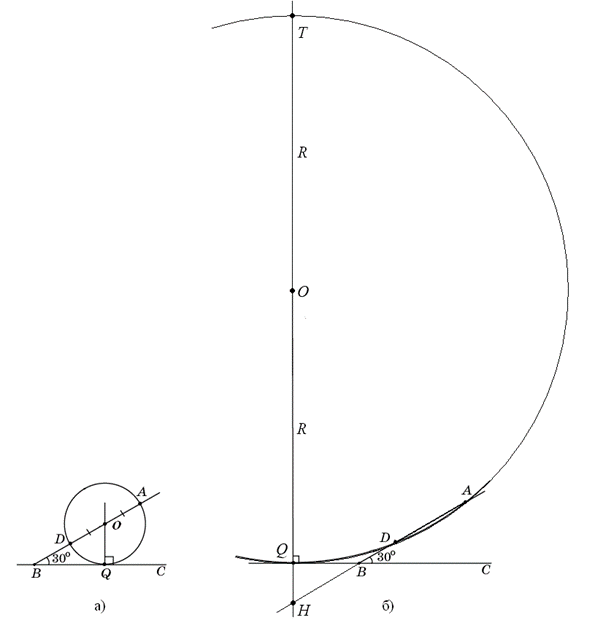
Ответ:
1 или 7.
Возможны другие формы записи ответа.
Например:
А) 1, 7;
Б) радиус окружности равен 7 или 1.
| Содержание критерия |
Баллы |
| Обоснованно получен верный ответ |
3 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой получено правильное значение искомой величины, или рассмотрены обе конфигурации, для которых получены значения искомой величины, неправильные из-за арифметических ошибок |
2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой получено значение искомой величины, неправильное из-за арифметической ошибки |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный
балл
|
3 |
Найдите все значения 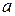 , при каждом из которых наименьшее значение функции , при каждом из которых наименьшее значение функции 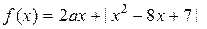 больше 1. больше 1.
Решение.
1. Функция 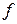 имеет вид: имеет вид:
a) при 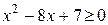 : : 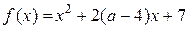 , а её график есть две части параболы с ветвями, направленными вверх, и осью симметрии , а её график есть две части параболы с ветвями, направленными вверх, и осью симметрии 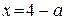 ; ;
б) при 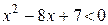 : : 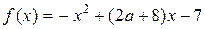 , а её график есть часть параболы с ветвями, направленными вниз. , а её график есть часть параболы с ветвями, направленными вниз.
Все возможные виды графика функции 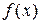 показаны на рисунках: показаны на рисунках:
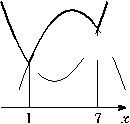
Рис. 1
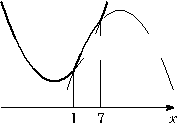
Рис. 3
|
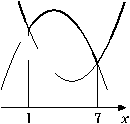
Рис. 2
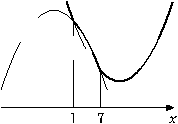
Рис. 4
|
2. Наименьшее значение функция 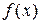 может принять только в точках может принять только в точках 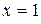 или или 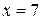 , а если , а если 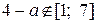 – то в точке – то в точке 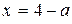 . .
3. Наименьшее значение функции 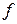 больше 1 тогда и только тогда, когда больше 1 тогда и только тогда, когда
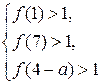  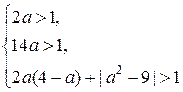  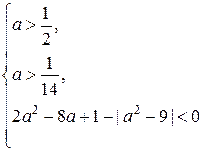 
 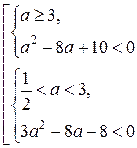  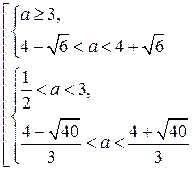 
 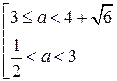  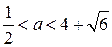 . .
Ответ:
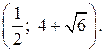
| Содержание критерия |
Баллы |
| Обоснованно получен правильный ответ |
4 |
| Получен верный ответ. Решение в целом верное, но либо имеет пробелы (например, не описаны необходимые свойства функции), либо содержит вычислительные ошибки |
3 |
| Верно рассмотрены все случаи раскрытия модулей. При составлении или решении условий на параметр допущены ошибки, в результате которых в ответе либо приобретены посторонние значения, либо часть верных значений потеряна |
2 |
| Хотя бы в одном из случаев раскрытия модуля составлено верное условие на параметр либо построен верный эскиз графика функции в целом |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный балл
|
4 |
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 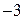 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 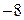 . .
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение.
Пусть среди написанных чисел 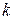 положительных, положительных, 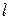 отрицательных и отрицательных и 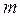 нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому 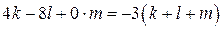 . .
а) Заметим, что в левой части приведённого выше равенства каждое слагаемое делится на 4, поэтому 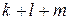 — количество целых чисел — делится на 4. По условию — количество целых чисел — делится на 4. По условию 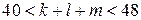 , поэтому , поэтому 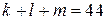 . Таким образом, написано 44 числа. . Таким образом, написано 44 числа.
б) Приведём равенство 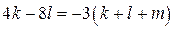 к виду к виду 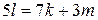 . Так как . Так как 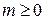 , получаем, что , получаем, что 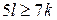 , откуда , откуда 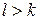 . Следовательно, отрицательных чисел больше, чем положительных. . Следовательно, отрицательных чисел больше, чем положительных.
воценка
) Подставим 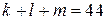 в правую часть равенства в правую часть равенства 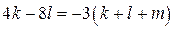 : : 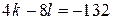 , откуда , откуда 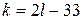 . Так как . Так как 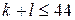 , получаем: , получаем: 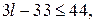 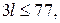 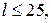 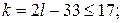 то есть положительных чисел не более 17. то есть положительных чисел не более 17.
впример
) Приведём пример, когда положительных чисел ровно 17. Пусть на доске 17 раз написано число 4, 25 раз написано число 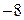 и два раза написан 0. Тогда и два раза написан 0. Тогда 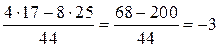 , указанный набор удовлетворяет всем условиям задачи. , указанный набор удовлетворяет всем условиям задачи.
Ответ:
а) 44; б) отрицательных; в) 17.
| Содержание критерия |
Баллы |
| Верно выполнены: а), б), впример
), воценка
) |
4 |
| Верно выполнены три пункта из четырёх: а), б), впример
), воценка
) |
3 |
| Верно выполнены два пункта из четырёх: а), б), впример
), воценка
) |
2 |
| Верно выполнен один пункт из четырёх: а), б), впример
), воценка
) |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный балл
|
4 |
|