 Федеральное агентство по образованию Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт экономики отраслей, бизнеса и администрирования
Кафедра экономики отраслей и рынков
Контрольная работа
по дисциплине
«Эконометрика»
Выполнил:
студентка группы 28ФВ-301
Яковлева Д.А.
Проверил:
Распопова Е.А.
Челябинск
2009
По некоторым территориям области известны значения среднесуточного душевого дохода в у.е. (фактор Х) и процент от общего дохода, расходуемого на покупку продовольственных товаров (фактор Y), табл.1. Требуется для характеристики зависимости Yот X рассчитать параметры линейной модели
Таблица 1
| № |
Федеральный округ |
Расходы на продовольственные товары (процент от общего дохода)
Фактор Y
|
Среднесуточный душевой доход (у.е.)
Фактор X
|
| 1 |
Магнитогорск |
68,8 |
45,1 |
| 2 |
Златоуст |
61,2 |
59,0 |
| 3 |
Копейск |
59,9 |
57,2 |
| 4 |
Миасс |
56,7 |
61,8 |
| 5 |
Еманжелинск |
55,0 |
58,8 |
| 6 |
Чебаркуль |
54,3 |
47,2 |
| 7 |
Пласт |
49,3 |
55,2 |
Предположим, что связь между среднесуточным душевым доходом в у.е. (фактор Х) и процентом от общего дохода, расходуемого на покупку продовольственных товаров (фактор Y), линейная. Для подтверждения нашего предположения построим поле корреляции.
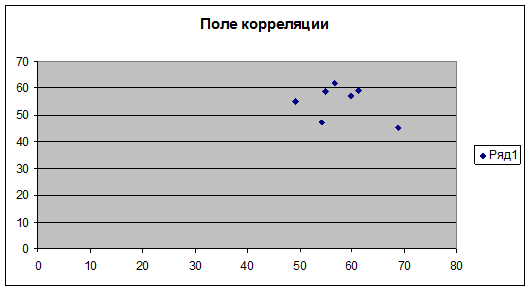
Рис. 1.
Для удобства дальнейших вычислений составим таблицу.
Таблица 2
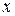 |
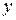 |
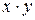 |
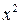 |
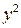 |
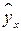 |
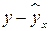 |
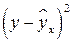 |
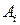 , % , % |
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 1 |
45,1 |
68,8 |
3102,88 |
2034,01 |
4733,44 |
61,27 |
7,52 |
56,61 |
10,94 |
| 2 |
59 |
61,2 |
3610,8 |
3481 |
3745,44 |
56,47 |
4,73 |
22,4 |
7,73 |
| 3 |
57,2 |
59,9 |
3426,28 |
3271,84 |
3588,01 |
57,09 |
2,81 |
7,89 |
4,69 |
| 4 |
61,8 |
56,7 |
3504,06 |
3819,24 |
3214,89 |
55,5 |
1,20 |
1,44 |
2,12 |
| 5 |
58,8 |
55 |
3234 |
3457,44 |
3025 |
56,55 |
-1,54 |
2,36 |
2,79 |
| 6 |
47,2 |
54,3 |
2562,96 |
2227,84 |
2948,49 |
60,55 |
-6,25 |
39,05 |
11,51 |
| 7 |
55,2 |
49,3 |
2721,36 |
3047,04 |
2430,49 |
57,78 |
-8,48 |
71,94 |
17,20 |
| ИТОГО |
384,3 |
405,2 |
22162,34 |
21338,41 |
23685,76 |
405,2 |
0 |
201,71 |
56,99 |
| Среднее значение |
54,9 |
57,89 |
3166,05 |
3048,34 |
3383,68 |
- |
- |
- |
8,14 |
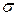 |
5,86 |
5,85 |
- |
- |
- |
- |
- |
- |
- |
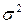 |
34,34 |
34,33 |
- |
- |
- |
- |
- |
- |
- |
Рассчитаем параметры линейного уравнения парной регрессии 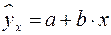 . Для этого воспользуемся формулами: . Для этого воспользуемся формулами:
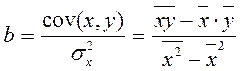
b = -0,35;
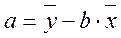
a = 76,88
Получили уравнение:. Y=76,88-0,35x
Т.е. с увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35%.
Уравнение линейной регрессии всегда дополняется показателем тесноты связи – линейным коэффициентом корреляции 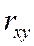 : :
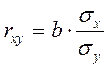
rxy
= -0,357
Связь умеренная обратная.
Коэффициент детерминации r2
xy
= 0,127 показывает, что уравнением регрессии объясняется 12,7% дисперсии результативного признака, а на долю прочих факторов приходится 87,3%.
Оценим качество уравнения регрессии в целом с помощью 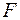 -критерия Фишера. Сосчитаем фактическое значение -критерия Фишера. Сосчитаем фактическое значение 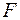 -критерия: -критерия:
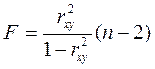
Fфакт=0,68
Fтабл.=6,61
Так как Fтабл
>Fфакт
при а=0,05, то необходимо принять гипотезу о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем 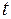 -критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции -критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
Реклама

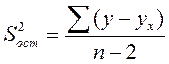
S2
ост
=40,34
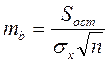
mb
=0,41
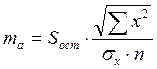
ma
= 22,62
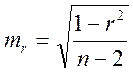
mr
= 0,42
ti
=ai
/ mi
Фактические значения 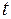 -статистик: -статистик:
tb
= -0,84
ta
= 3,4
tr
= 0,42
Табличное значение 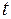 -критерия Стьюдента при -критерия Стьюдента при 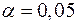 и числе степеней свободы v=5 есть tтабл
= 2,5706. Так как tb
<tтабл
, ta
>tтабл
, и tr
<tтабл,
то признаем случайную статистическую значимость параметров регрессии и показателя тесноты связи. и числе степеней свободы v=5 есть tтабл
= 2,5706. Так как tb
<tтабл
, ta
>tтабл
, и tr
<tтабл,
то признаем случайную статистическую значимость параметров регрессии и показателя тесноты связи.
Рассчитаем доверительные интервалы для параметров регрессии 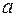 и и 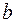 : : 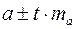 и и 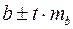 . Получим, что . Получим, что 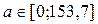 и и 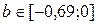 . .
Средняя ошибка аппроксимации (находим с помощью столбца 10 таблицы 2; 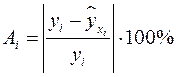 ) ) 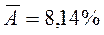 говорит о том, что в среднем расчетные значения отклоняются от фактических на 8,14% говорит о том, что в среднем расчетные значения отклоняются от фактических на 8,14%
Найдем прогнозное значение результативного фактора 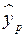 при значении признака-фактора, составляющем 110% от среднего уровня при значении признака-фактора, составляющем 110% от среднего уровня 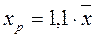 , xp
= 60,39 т.е. найдем расходы, если доходы семьи составят 60,39 у.е. , xp
= 60,39 т.е. найдем расходы, если доходы семьи составят 60,39 у.е.
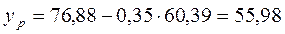
Значит, если доходы составят 60,39 у.е.., то расходы – 55,98у.е..
Найдем доверительный интервал прогноза. Ошибка прогноза
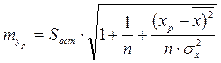
 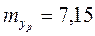
а доверительный интервал (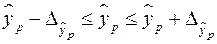 ), где ), где  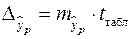 и и 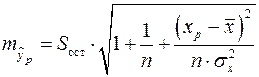
37,57<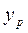 <74,36 <74,36
Т.е. прогноз является статистически надежным.
Теперь на одном графике изобразим исходные данные и линию регрессии:
 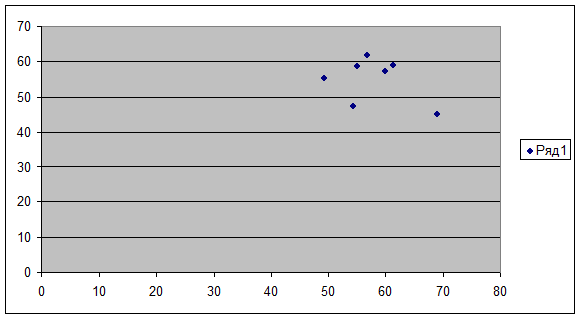
Рис.2
Таблица 3. (из Excel)
| ВЫВОД ИТОГОВ |
| Регрессионная статистика
|
| Множественный R |
0,353257293 |
| R-квадрат |
0,124790715 |
| Нормированный R-квадрат |
-0,050251142 |
| Стандартная ошибка |
6,351507436 |
| Наблюдения |
7 |
| Дисперсионный анализ |
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
1 |
28,76033785 |
28,76033785 |
0,712919283 |
0,436999565 |
| Остаток |
5 |
201,7082336 |
40,34164671 |
| Итого |
6 |
230,4685714 |
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение |
76,87708484 |
22,62016613 |
3,398608321 |
0,019280151 |
18,73009669 |
135,024073 |
18,73009669 |
135,024073 |
| Переменная X 1 |
-0,345926604 |
0,409697942 |
-0,844345476 |
0,436999565 |
-1,399088692 |
0,707235484 |
-1,399088692 |
0,707235484 |
|