Содержание
Введение
1. История развития теории вероятностей и математической статистики
2. Теоретические основы статистической обработки экспериментальных данных
3. Статистический анализ выборочной совокупности
Заключение
Список литературы
Приложение
Введение
Математическая статистика – это раздел математики, в котором изучаются математические методы планирования экспериментов, систематизации, обработки и использования статистических данных для научных и практических целей. В математической статистике предполагается, что результаты опытных данных и наблюдений являются реализацией случайных величин или процессов, имеющих те или иные законы распределения.
Методы математической статистики обосновывают способы группировки и анализа статистических сведений о качественных и количественных признаках объектов различной природы. Проведение обследования каждого объекта большой совокупности относительно интересующего признака или физически невозможно или экономически нецелесообразно. Для установления статистических закономерностей случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.
Цель данной курсовой работы – исследование 3-х выборочных совокупностейобъемом по сто наблюдений каждая, которое включает следующие этапы:
1) составление статистических распределений выборочных совокупностей;
2) нахождение параметров статистических распределений;
3) установление законов распределения выборочных совокупностей.
1.
История развития теории вероятностей и математической статистики
Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса (1777–1855), который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных (с целью уточнения орбиты малой планеты Церера). Его именем часто называют одно из наиболее популярных распределений вероятностей – нормальное, а в теории случайных процессов основной объект изучения – гауссовские процессы.
В конце XIX в. – начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего К. Пирсон (1857–1936) и Р.А. Фишер (1890–1962). В частности, Пирсон разработал критерий «хи-квадрат» проверки статистических гипотез, а Фишер – дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров.
Реклама

В 30-е годы ХХ в. поляк Ежи Нейман (1894–1977) и англичанин Э. Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А.Н. Колмогоров (1903–1987) и член-корреспондент АН СССР Н.В. Смирнов (1900–1966) заложили основы непараметрической статистики. В сороковые годы ХХ в. румын А. Вальд (1902–1950) построил теорию последовательного статистического анализа.
Понятие случайного процесса введено в XX столетии и связано с именами А.Н. Колмогорова (1903–1987), А.Я. Хинчина (1894–1959), Е.Е. Слуцкого (1880–1948), Н. Винера (1894–1965). Это понятие в наши дни является одним из центральных не только в теории вероятностей, но также в естествознании, инженерном деле, экономике, организации производства, теории связи. Теория случайных процессов принадлежит к категории наиболее быстро развивающихся математических дисциплин. Несомненно, что это обстоятельство в значительной мере определяется ее глубокими связями с практикой. XX век не мог удовлетвориться тем идейным наследием, которое было получено от прошлого. Для исследования изменения во времени теория вероятностей конца XIX – начала XX века не имела ни разработанных частных схем, ни тем более общих приемов. А необходимость их создания буквально стучала в окна и двери математической науки. Изучение броуновского движения в физике подвело математику к порогу создания теории случайных процессов. В исследованиях датского ученого А.К. Эрланга (1878–1929) была открыта новая важная область, связанная с изучением загрузки телефонных сетей.
Во втором десятилетии XX века начались исследования динамики биологических популяций. Итальянский математик Вито Вольтерра (1860–1940) разработал математическую теорию этого процесса на базе чисто детерминистских соображений. Позднее ряд биологов и математиков развивали его идеи уже на основе стохастических представлений. Многие физические явления для своего изучения требуют умения вычислять вероятность того, что определенная доля молекул успеет за заданный промежуток времени перейти из одной области пространства в другую.
Теория броуновского движения, исходящая из теоретико-вероятностных предпосылок, была разработана в 1905 г. двумя известными физиками М. Смолуховским (1872–1917) и А. Эйнтейном (1879–1955). В частности, именно с этих работ, как, впрочем, и с работ Эрланга, проявился широкий интерес к процессу Пуассона. Впрочем, сам Пуассон ввел в рассмотрение только распределение Пуассона, но он заслужил, чтобы его имя произносилось и при рассмотрении случайных процессов, связанных с его распределением. Это не единственный случай, когда в честь того или другого исследователя новым понятиям присваиваются их имена, хотя до этих понятий они и не доходили. Теперь широко распространены гауссовские случайные процессы, хотя сам Гаусс о них не имел никакого представления, да и само исходное распределение задолго до его рождения было получено Муавром, Лапласом и др.
Реклама

В теории же ошибок измерений одновременно с Гауссом к нему пришел также Лежандр. Попытка изучения средствами теории вероятностей явления диффузии была предпринята в 1914 г. двумя известными физиками – М. Планком (1858–1847) и А. Фоккером (1887–1972). Н. Винер в середине двадцатых годов при изучении броуновского движения ввел в рассмотрение процесс, получивший название винеровского процесса (процесса броуновского движения). Мы должны упомянуть еще о двух важных группах исследований, начатых в разное время и по разным поводам. Во-первых, эта работы А.А. Маркова (1856–1922) по изучению цепных зависимостей. Во-вторых, работы Е.Е. Слуцкого (1880–1948) по теории случайных функций. В 1931 г. была опубликована большая статья А.Н. Колмогорова – Об аналитических методах в теории вероятностей, а через три года – работа А.Я. Хинчина – Теория корреляции стационарных стохастических процессов, которые следует считать началом построения общей теории случайных процессов. В первой из этих были заложены основы марковских процессов, а во второй – основы стационарных процессов. Они были источником огромного числа последующих исследований, среди которых следует отметить статью В. Феллера – К теории стохастических процессов (1936), давшую интегро-дифференциальные уравнения для скачкообразных марковских процессов. Обе только что упомянутые основополагающие работы содержат не только математические результаты, но и глубокий философский анализ причин, послуживших исходным пунктом для построения основ теории случайных процессов.
Математическая статистика бурно развивается и в настоящее время. Так, за последние 40 лет можно выделить четыре принципиально новых направления исследований:
– разработка и внедрение математических методов планирования экспериментов;
– развитие статистики объектов нечисловой природы как самостоятельного направления в прикладной математической статистике;
– развитие статистических методов, устойчивых по отношению к малым отклонениям от используемой вероятностной модели;
– широкое развертывание работ по созданию компьютерных пакетов программ, предназначенных для проведения статистического анализа данных.
2. Теоретические основы статистической обработки экспериментальных данных
Функция распределения вероятностей случайной величины
Функцией распределения называют функцию F(х), определяющую вероятность того, что непрерывная случайная величина Х в результате испытания примет значение, меньшее числа х:
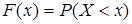 . .
Свойства функции распределения:
1) значения функции распределения принадлежат отрезку [0,1]: 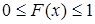 ; ;
2) F(x) – неубывающая функция, т.е. 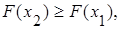 если если 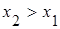 ; ;
3) вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: 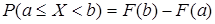 ; ;
4) если все возможные значения случайной величины принадлежат интервалу (a, b), то 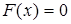 при при 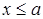 и и 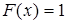 при при 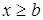 . .
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
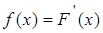 . .
Свойства плотности распределения:
1) плотность распределения – неотрицательная функция: f(x)≥0;
2) несобственный интеграл от плотности распределения в пределах от –∞ до +∞ равен единице: 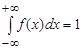 ; ;
3) вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (х1
; х2
), равна определенному интегралу от плотности распределения, взятому от a до b:
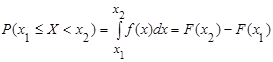 . (1) . (1)
Полученный результат геометрически отражает тот факт, что вероятность попадания непрерывной случайной величины в заданный интервал (х1
; х2
) равна площади криволинейной трапеции, ограниченной осью Ох, графиком плотности распределения f(x) и прямыми 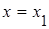 и и 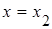 . .
1.2. Числовые характеристики случайных величин
Математическое ожидание М(Х) непрерывной случайной величины, распределенной на интервале (х1
; х2
), характеризует ее среднее значение и определяется по формуле
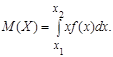 (2) (2)
ДисперсияD(X) непрерывной случайной величины, распределенной на интервале (х1
; х2
), характеризует ее рассеяние относительно математического ожидания и определяется по формуле
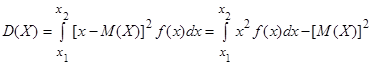 . (3) . (3)
Если возможные значения непрерывной случайной величины принадлежат всей числовой оси Ох, то математическое ожидание и дисперсия определяются по формулам
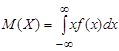 и и 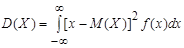 . .
Среднее квадратическое отклонение σ(Х) случайной непрерывной величины определяется по формуле
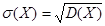 . (4) . (4)
Начальным моментом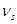 порядка s случайной величины Х называют математическое ожидание величины Хs
: порядка s случайной величины Х называют математическое ожидание величины Хs
:
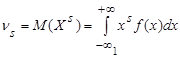 . (5) . (5)
Начальный момент первого порядка случайной величины Х соответствует ее математическому ожиданию.
Центральным моментом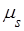 порядка s случайной величины Х называют математическое ожидание величины порядка s случайной величины Х называют математическое ожидание величины 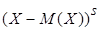 : :
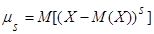 . (6) . (6)
Центральные и начальные моменты случайной величины Х связаны следующими соотношениями:
1) 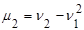 ; ;
2) 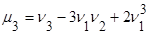 ; ;
3) 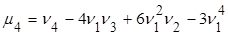 . .
Центральный момент третьего порядка 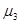 случайной величины Х характеризует асимметрию (скошенность) распределения и служит для вычисления коэффициента асимметрии случайной величины Х характеризует асимметрию (скошенность) распределения и служит для вычисления коэффициента асимметрии 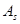 , который определяется по формуле , который определяется по формуле
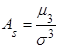 . (7) . (7)
Асимметрия положительна, если «длинная часть» кривой плотности распределения расположена справа от математического ожидания. Асимметрия отрицательна, если «длинная часть» кривой распределения расположена слева от математического ожидания.
Центральный момент четвертого порядка 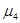 случайной величины Х характеризует «крутость» или островершинность графика ее плотности распределения и служит для вычисления эксцесса случайной величины Х характеризует «крутость» или островершинность графика ее плотности распределения и служит для вычисления эксцесса
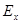 , который определяется по формуле , который определяется по формуле
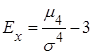 . (8) . (8)
Эксцесс положительный, если кривая распределения имеет острую вершину. Эксцесс отрицательный, если кривая распределения имеет пологую вершину.
Равномерное распределение вероятностей
Распределение вероятностей называют равномерным, если на интервале (a; b), которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:
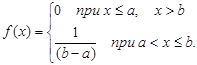 (9) (9)
Функция равномерного распределения на интервале (a; b) имеет вид:
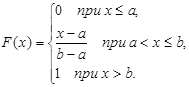
Характеристики равномерного распределения определяются по формулам (2) – (4), (7), (8):
1) математическое ожидание 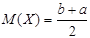 ; ;
2) дисперсия 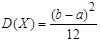 ; ;
3) среднее квадратическое отклонение 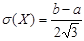 ; ;
4) асимметрия 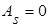 ; ;
5) эксцесс 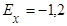 . .
Вероятность попадания случайной величины Х, распределенной по равномерному закону, в заданный интервал (х1
; х2
) определяется по формуле (1)
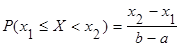 . .
Показательное распределение
Показательным (экспоненциальным) называют распределение непрерывной случайной величины Х, которое описывается плотностью
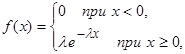 (10) (10)
где λ – постоянная положительная величина.
Функция показательного распределения имеет вид:
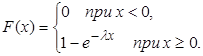
Характеристики показательного распределения определяются по формулам (2) – (4):
1) математическое ожидание 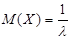 ; ;
2) дисперсия 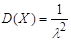 ; ;
3) среднее квадратическое отклонение 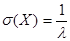 . .
Вероятность попадания случайной величины Х, распределенной по показательному закону, в заданный интервал (х1
; х2
) определяется по формуле (1)
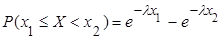 . (11) . (11)
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
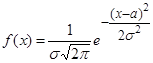 (12) (12)
Математическое ожидание нормального распределения равно параметру а. Среднее квадратическое отклонение нормального распределения равно параметру σ. Коэффициент асимметрии 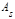 и эксцесс и эксцесс 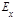 нормального распределения равны нулю: нормального распределения равны нулю: 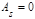 и и 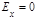 . .
Вероятность попадания нормально распределенной случайной величины Х в заданный интервал (х1
; х2
) определяется по формуле (1):
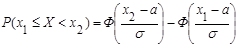 , (13) , (13)
где Ф(х) – функция Лапласа,
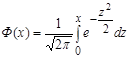 . (14) . (14)
4.
Статистический анализ выборочной совокупности
Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов. Объемом n выборочной совокупности называют число объектов этой совокупности.
Интервальным статистическим распределением выборки называют перечень интервалов и соответствующих им частот ni
или относительных частот 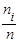 . .
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению 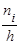 (плотность частоты). (плотность частоты).
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 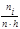 (плотность относительной частоты). (плотность относительной частоты).
Для распределения наблюдений по интервалам необходимо найти длину интервала h, определяемую как отношение разности между максимальным Xma
х
и минимальным Xmin
элементами выборки к количеству интервалов k
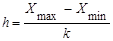 . (15) . (15)
Количество интервалов k (целое число) целесообразно выбрать не менее 7, но и не более 15 или определить по формуле Старджесса
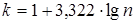 , (16) , (16)
где n – объем выборки.
Если k, вычисляемое по формуле Старджесса, нецелое число, то в качестве числа интервалов можно ближайшее к k целое число, не меньшее k.
Статистические оценки параметров распределения
Выборочной средней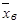 называют среднее арифметическое значение признака выборочной совокупности. Если все значения х1
, х2
, …., хn
выборки объема n различны, то называют среднее арифметическое значение признака выборочной совокупности. Если все значения х1
, х2
, …., хn
выборки объема n различны, то
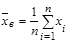 . .
Если значения признака х1
, х2
, …., хk
имеют соответственно частоты n1
, n2
, …..nk
, причем n1
+n2
+……+nk
=n, то
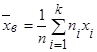 . (17) . (17)
Для характеристики рассеяния значений количественного признака Х выборки вокруг своего среднего значения вводят такой параметр как выборочная дисперсия.
Выборочной дисперсиейDв
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 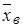 . Если все значения х1
, х2
, …., хn
признака различны, то . Если все значения х1
, х2
, …., хn
признака различны, то
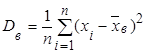 = =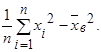
Если значения признака х1
, х2
, …., хk
имеют соответственно частоты n1
, n2
, …..nk
, причем n1
+n2
+……+nk
=n, то
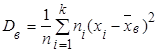 . (18) . (18)
Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:
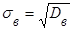 . (19) . (19)
Начальный эмпирический момент 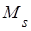 порядка s статистического распределения определяют по формуле порядка s статистического распределения определяют по формуле
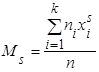 , (20) , (20)
где xi
– наблюдаемое значение признака, ni
– частота наблюдаемого значения признака, n – объем выборки.
Начальный эмпирический момент первого порядка равен выборочной средней 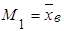 . .
Центральный эмпирический момент 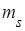 порядка sстатистического распределения определяют по формуле порядка sстатистического распределения определяют по формуле
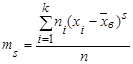 . .
Центральный эмпирический момент второго порядка равен выборочной дисперсии 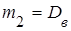 . .
Коэффициент асимметрии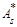 статистического распределения определяется по формуле статистического распределения определяется по формуле
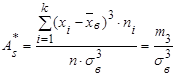 . (22) . (22)
Эксцесс 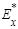 статистического распределения определяется по формуле статистического распределения определяется по формуле
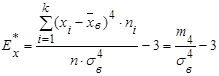 . (23) . (23)
Относительной характеристикой рассеивания случайной величины выступает коэффициент вариации V, который вычисляется как отношение среднего квадратического отклонения и выборочной средней по формуле
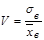 . (24) . (24)
Метод моментов
Метод моментов – это определение неизвестных параметров статистического распределения путем приравнивания теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.
Для нахождения параметра λ показательного распределения необходимо приравнять начальный момент первого порядка показательного распределения начальному моменту первого порядка эмпирического распределения:
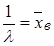 (25) (25)
Для нахождения параметров а и σ нормального распределения необходимо:
1) приравнять начальный момент первого порядка нормального распределения к начальному моменту первого порядка эмпирического распределения:
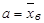 ; (26) ; (26)
2) центральный момент второго порядка нормального распределения к центральному моменту второго порядка эмпирического распределения:
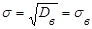 . (27) . (27)
Для нахождения параметров a и bравномерного распределениянеобходимо:
1) приравнять начальный момент первого порядка равномерного распределения к начальному моменту первого порядка эмпирического распределения:
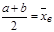 ; ;
2) центральный момент второго порядка равномерного распределения к центральному моменту второго порядка эмпирического распределения:
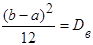 . .
Параметры равномерного распределения a и b можно определить по формулам
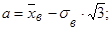 (28) (28)
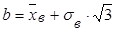 . (29) . (29)
Начальные эмпирические моменты третьего 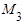 и четвертого и четвертого 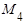 порядков статистического распределения приравниваются соответственно к начальным моментам третьего порядков статистического распределения приравниваются соответственно к начальным моментам третьего 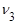 и четвертого и четвертого 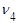 порядков случайной величины: порядков случайной величины: 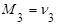 и и 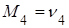 . .
Центральные эмпирические моменты третьего 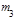 и четвертого и четвертого 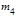 порядков статистического распределения приравниваются соответственно к центральным моментам третьего порядков статистического распределения приравниваются соответственно к центральным моментам третьего 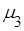 и четвертого и четвертого 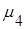 порядков случайной величины: порядков случайной величины: 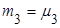 и и 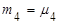 . .
Проверка статистических гипотез
Установление закона распределения выборочной совокупности проводится через проверку статистических гипотез.
Статистической называют гипотезу о виде неизвестного распределения. Статистические гипотезы бывают двух видов: нулевая (выдвигаемая) гипотеза Н0
и конкурирующая (противоречащая нулевой) Н1
.
Проведение проверки статистическими методами приводит к появлению ошибок двух родов: 1) ошибка первого рода – отвержение правильной гипотезы; 2) ошибка второго рода – принятие неправильной гипотезы.
Вероятность совершить ошибку первого рода называют уровнем значимости и обозначают через α. Наиболее часто уровень значимости принимают 0,05, что означает наличие риска отвергнуть правильную гипотезу в пяти случаях из ста.
Для проверки нулевой гипотезы используется специально подобранная случайная величина, которая называется статистическим критерием.
Наблюдаемым значением критерия называют его значение, вычисленное по выборке.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезыназывают совокупность значений критерия, при которых нулевую гипотезу принимают.
Критической точкой называют точку, отделяющую критическую область от области принятия гипотезы. Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку.
Основной принцип проверки статистических гипотез формулируется следующим образом: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают. Для проверки гипотезы о закономерности распределения выборочной совокупности применяется критерий Пирсона 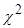 (хи-квадрат), критические точки (хи-квадрат), критические точки 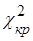 которого находят по таблице. которого находят по таблице.
Нулевую гипотезу следует принимать, если наблюдаемое значение критерия Пирсона меньше значения критической точки 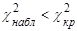 . Нулевую гипотезу следует отвергнуть, если наблюдаемое значение критерия Пирсона больше значения критической точки . Нулевую гипотезу следует отвергнуть, если наблюдаемое значение критерия Пирсона больше значения критической точки 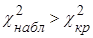 . .
Для вычисления наблюдаемого значения критерия Пирсона 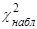 необходимо сравнить эмпирические необходимо сравнить эмпирические 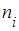 и теоретические и теоретические 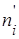 частоты каждого интервала статистического распределения выборки по формуле частоты каждого интервала статистического распределения выборки по формуле
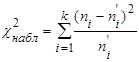 , (30) , (30)
где k – количество интервалов.
Эмпирическая частота 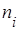 равна количеству наблюдений в выборке, попавших в данный интервал. Теоретическая частота равна количеству наблюдений в выборке, попавших в данный интервал. Теоретическая частота 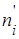 вычисляется по формуле вычисляется по формуле
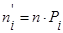 , (31) , (31)
где Рi
– вероятность попадания случайной величины Х теоретического распределения в частичный интервал 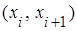 , n – объем выборки. , n – объем выборки.
Выбор теоретического распределения определяется примерным совпадением вида гистограммы относительных частот статистического распределения с графиком плотности соответствующего распределения случайной величины Х (рис. 1, 2, 3). Результатом проведенного сравнительного анализа выступает выдвижение гипотезы о виде распределения выборочной совокупности и ее последующая проверка.
Для подтверждения выдвигаемой гипотезы сравниваются:
1) коэффициент асимметрии 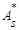 статистического распределения с коэффициентами асимметрии статистического распределения с коэффициентами асимметрии 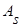 равномерного и нормального распределений ( равномерного и нормального распределений (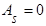 ); );
2) эксцесс 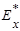 статистического распределения с эксцессами статистического распределения с эксцессами 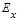 равномерного ( равномерного (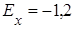 ) или нормального распределений ( ) или нормального распределений (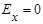 ); );
3) коэффициент вариации V статистического распределения с коэффициентами вариации показательного (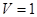 ) распределения. ) распределения.
Характеристики выборочных совокупностей
| Выборка |
Характеристики |
| Xmin
|
Xmax
|
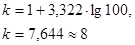 |
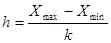
|
| 1 |
5,1 ≈ 5 |
18,76 ≈ 20 |
6 |
2,5 |
| 2 |
0,18 ≈ 0 |
22,06 ≈ 25 |
5 |
5 |
| 3 |
0,03 ≈ 0 |
30,76 ≈ 35 |
7 |
5 |
Центральные эмпирические моменты выборок
| Параметры |
Выборка |
| 1 |
2 |
3 |
| m
2
|
16,48 |
19,62 |
48,58 |
| m
3
|
1,19 |
-3,79 |
513,41 |
| m
4
|
488,96 |
1053,94 |
11404,22 |
Параметры статистических распределений выборок
| Параметры |
Выборка |
| 1 |
2 |
3 |
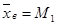 |
12,19 |
12,54 |
12,19 |
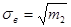 |
4,06 |
4,43 |
6,97 |
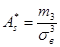 |
0,02 |
-0,04 |
1,5 |
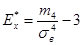 |
-1,20 |
-0,26 |
1,83 |
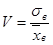 |
0,33 |
0,35 |
0,57 |
- выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22;
- выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43;
- выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.
Результаты сравнения коэффициентов асимметрии, эксцессов и коэффициентов вариации выборочных совокупностей не противоречат выдвинутым гипотезам:
- коэффициент асимметрии и коэффициент вариации V=0,33 выборочной совокупности 1 сравнимы с соответствующими параметрами равномерного распределения (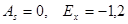 ); );
- коэффициент асимметрии A*
s
=-0,04, эксцесс E*
s
=-0,26, выборочной совокупности 2 сравнимы с соответствующими параметрами нормального распределения (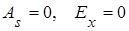 ); );
- коэффициент вариации V=0,57 выборочной совокупности 3 сравним с соответствующим параметром показательного распределения (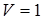 ). ).
Проверка гипотезы о равномерном распределении выборки 1
| Нулевая гипотеза Н
0
:выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22. |
| Число степеней свободы: r=3. |
| Уровень значимости α
=0,05. |
Критическая точка 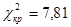 |
Наблюдаемое значение критерия Пирсона 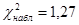 |
Критическая область 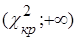 : : 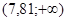 |
Область принятия гипотезы 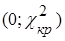 : : 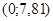 |
Условие принятия Н
0
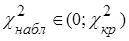 :
: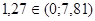
|
Условие непринятия Н
0
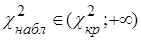 : : 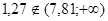 |
| Результат проверки гипотезы: выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22. |
Проверка гипотезы о нормальном распределении выборки 2
| Нулевая гипотеза Н
0
: выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43. |
| Число степеней свободы: r=2. |
| Уровень значимости α
=0,05 |
Критическая точка 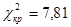 |
Наблюдаемое значение критерия Пирсона 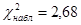 |
Критическая область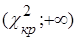 : : 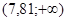 |
Область принятия гипотезы 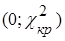 : : 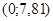 |
Условие принятия Н
0
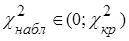 : : 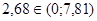
|
Условие непринятия Н
0
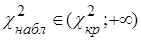 : : 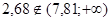 |
| Результат проверки гипотезы: выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43. |
Проверка гипотезы о показательном распределении выборки 3
| Нулевая гипотеза Н
0
:Выборочная совокупность 3 имеет показательное распределение с параметром l=0,14. |
| Число степеней свободы: r=5 |
| Уровень значимости α
=0,05 |
Критическая точка 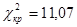 |
Наблюдаемое значение критерия Пирсона 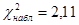 |
Условие принятия Н
0
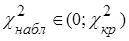 :
: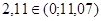
|
| Результат проверки гипотезы: выборочная совокупность 3 имеет показательное распределение с параметром l=0,14. |
Заключение
С помощью программы Excel был проведен статистический анализ 3-х выборочных совокупностей и было установлено, что:
- выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22;
- выборочная совокупность 1 имеет нормальное распределение с параметрами a=12,54 и s=4,43;
- выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.
Список литературы
1. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учеб. пособие для вузов. 4-е изд., перераб. и доп. М.: Высш. шк., 2002. - 448 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов. 9-е изд., стер. М.: Высш. шк., 2003. - 479 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов. Изд. 4-е, стер. – М.: Высш. шк., 1997. - 400 с.
4. Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. Учебное пособие для вузов. Издание 2-е исправленное и дополненное. Ростов на Дону: Феникс, 2002. - 400 с.
5. Елисеева Н.Н. и др. Теория статистики с основами теории вероятностей. - М.: ЮНИТИ, 2001. - 446 с.
6. Куликова О.В., Тимофеева Г.А., Чуев Н.П. Исследование выборочных совокупностей с применением программы Excel – Екатеринбург.: УрГУПС, 2003. - 76 с.
7. Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб. пособие. – М.: Финансы и статистика, 2002. - 368 с.
8. Гнеденко Б.В. Очерки по истории математики в России. – М.; Л.: Гос. изд-во техн.-теорет. лит., 1946. – 245 с.
|