«Брестский государственный университет имени А.С. Пушкина»
Реферат
Петрусевич Николай Николаевич
Брест 2010
Евдокс Книдский (ок.408-355 гг. до н.э.)
О жизни Евдокса известно немного. Родился в Книде, на юго-западе Малой Азии.
Учился медицине, потом математике (у пифагорейца Архита в Италии), затем присоединился к школе Платона в Афинах. Около года провёл в Египте, изучал астрономию в Гелиополе. Позднее Евдокс переселился в город Кизик на Мраморном море, основал там собственную математико-астрономическую школу, читал лекции по философии, астрономии и метеорологии.
Евдокс Книдский известен прежде всего как математик и астроном, но кроме того он писал книги по философии, географии, музыке и медицине. О жизни Евдокса известно следующее. В молодости он изучал математику у Архита в Таренте и медицину у Филистиона в Сицилии. 23-х лет он прибыл в Афины и, будучи очень бедным, поселился в гавани Пирея, откуда ежедневно ходил пешком в платоновскую Академию и обратно. Позднее при содействии друзей, он совершил путешествие в Египет, где набирался астрономических знаний у жрецов Гелиопля. Вернувшись в Грецию, он основал собственную школу в Кизике (на берегу Мраморного моря).
По своим философским взглядам Евдокс в ряде вопросов примыкал к Платону. Он признавал теорию идей, но в отличие от Платона полагал, что идеи как-то "примешиваются" к чувственно воспринимаемым предметам. Евдокс бесспорно был великим математиком. Развивая достижения Архита и Теэтета в области теории пропорций, он построил общую теорию отношений, основанную на новом определении величины. Если раньше теоремы теории отношений приходилось доказывать отдельно для чисел, отрезков и площадей, то понятие величины, введенное Евдоксом, включало в себя как числа, так и любые непрерывные величины. Другим важнейшим вкладом Евдокса в математику была разработка так называемого "метода исчерпывания", заложившего основы теории пределов и подготовившего почву для дальнейшего развития математического анализа. Для истории астрономии значения Евдокса было, пожалуй, еще более значительным. Фактически его можно считать создателем античной теоретической астрономии как самостоятельной науки. Евдокс был не только теоретиком, но и первоклассным астрономом-наблюдателем. При своей школе в Кизике он организовал первую греческую обсерваторию, где его ученики вели систематические наблюдения за небесными светилами. Он дал детальное описание созвездий, видимых на широте Греции, составил каталог звездного неба. Получив широкую известность, Евдокс еще раз побывал в Афинах, где беседовал с Платоном на философские темы. Умер он 53-х лет отроду на своей родине, Книде.
Реклама

Общая теория отношений
Числовые системы древних греков ограничивались натуральными числами и их отношениями (дробями, рациональными числами). Однако ещё пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, то есть отношение их длин не может быть представлено рациональным числом. Стало понятно, что пифагорейская арифметика должна быть каким-то образом расширена с тем, чтобы включать все результаты измерений. Это и сделал Евдокс. Его теория дошла до нас в изложении Евклида (Начала, книга V).
В дополнение к числам Евдокс ввёл более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона.[1] Этот подход снимает проблему несоизмеримости. По существу, теория отношений Евдокса — это геометрическая модель вещественных чисел. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Признание иррациональностей как особого вида чисел произошло много позднее, под влиянием индийских и исламских математических школ.
В начале своего построения Евдокс дал аксиоматику для сравнения величин. Все однородные величины сравнимы между собой, и для них определены две операции: отделение части и соединение (взятие кратного). Однородность величин сформулирована в виде аксиомы, известной также как аксиома Архимеда: «Говорят, что величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга».
Далее Евдокс рассматривает отношения между величинами и определяет для них равенство: отношения a:b и c:d равны, если для любых натуральных m, n выполняется одно из трёх соотношений:
либо ma < nb и mc < nd;
либо ma = nb и mc = nd;
либо ma > nb и mc > nd.
В современной формулировке, это означает, что между a:b и c:d нельзя вставить рациональное число.
Реклама

Далее Евдокс аккуратно выводит свойства отношений: транзитивность, упорядоченность и т. д.
Классическая теория Дедекинда для построения вещественных чисел поразительно похожа на изложение Евдокса. Соответствие между ними устанавливается так: пусть заданы две величины Евдокса a, b; дробь m/n отнесём к классу A, если ma > nb, иначе — к классу B. Тогда классы A и B определяют дедекиндово сечение поля рациональных чисел Q. Осталось отождествить отношение по Евдоксу b:a с этим дедекиндовым числом.
Отметим, однако, что у Евдокса отсутствует аналог аксиомы непрерывности, и ниоткуда не следует, что всякое сечение Q определяет вещественное число.
Метод исчерпывания
Это своего рода античный анализ криволинейных фигур. Обоснование этого метода не опирается на актуальные бесконечно малые, но неявно включает понятие предела. Название «метод исчерпывания» предложил в 1647 году Грегуар де Сен-Венсан (фр.Grégoire de Saint-Vincent
, 1584-1667), в античные времена у метода не было специального названия. Метод заключался в следующем: для нахождения площади (или объёма) некоторой фигуры в эту фигуру вписывалась монотонная последовательность других фигур и доказывалось, что их площади (объёмы) неограниченно приближаются к площади (объёму) искомой фигуры. Затем вычислялся предел последовательности площадей (объёмов), для чего выдвигалась гипотеза, что он равен некоторому A и доказывалось, что обратное приводит к противоречию. Поскольку общей теории пределов не было (греки избегали понятия бесконечности), все эти шаги, включая обоснование единственности предела, повторялись для каждой задачи. В такой форме метод исчерпывания хорошо вписывался в строго дедуктивное построение античной математики, однако имел несколько существенных недостатков. Во-первых, он был исключительно громоздким. Во-вторых, не было никакого общего метода для вычисления предельного значения A; Архимед, например, нередко выводил его из механических соображений или просто интуитивно угадывал. Наконец, этот метод не пригоден для нахождения площадей бесконечных фигур. С помощью метода исчерпывания Евдокс строго доказал ряд уже известных в те годы открытий (площадь круга, объём пирамиды и конуса).
Наиболее плодотворным этот метод стал в руках выдающегося последователя Евдокса, Архимеда, который смог его значительно усовершенствовать и виртуозно применял для многих новых открытий. В средние века европейские математики также применяли метод исчерпывания, пока он не был вытеснен сначала более мощным и технологичным методом неделимых, а затем — математическим анализом.
Пифагор Самосский (ок. 580 - ок. 500 до н. э.)
Биография
Пифагор Самосский (ок. 580 - ок. 500 до н. э.) древнегреческий математик и философ-идеалист.
Родителями Пифагора были Мнесарх и Партенида с Самоса. Мнесарх был камнерезом (Диоген Лаэртский); по словам же Порфирия он был богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора.[2] Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.
Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». В частности, Пифия сообщила Мнесарху, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. Поэтому, на радостях, Мнесарх дал жене новое имя Пифаида и дал имя ребенку Пифагор. Пифаида сопровождала мужа в его поездках, и Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.
По словам античных авторов Пифагор встретился чуть ли не со всеми известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание. В популярной литературе иногда приписывают Пифагору Олимпийскую победу в боксе, путая Пифагора-философа с его тёзкой (Пифагором, сыном Кратета с Самоса), который одержал свою победу на 48-х Играх за 18 лет до рождения знаменитого философа.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.
Ямвлих пишет, что Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока, наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.
По Порфирию, Пифагор покинул Самос из-за несогласия с тиранической властью Поликрата в 40-летнем возрасте. Так как эти сведения основываются на словах Аристоксена, источника IV века до н. э., то считаются относительно достоверными. Поликрат пришёл к власти в 535 до н. э., отсюда дата рождения Пифагора оценивается в 570 до н. э., если допустить, что он уехал в Италию в 530 до н. э. Ямвлих сообщает, что Пифагор переехал в Италию в 62-ю Олимпиаду, то есть в 532—529 гг. до н. э. Эти сведения хорошо согласуются с Порфирием, но полностью противоречат легенде самого Ямвлиха (вернее, одного из его источников) о вавилонском пленении Пифагора. Точно неизвестно, посещал ли Пифагор Египет, Вавилон или Финикию, где набрался по легендам восточной мудрости. Диоген Лаэртский цитирует Аристоксена, который говорил, что учение своё, по крайней мере, что касается наставлений по образу жизни, Пифагор воспринял от жрицы Фемистоклеи Дельфийской, то есть в местах не столь отдалённых для греков.
Разногласия с тираном Поликратом вряд ли могли послужить причиной отъезда Пифагора, скорее ему требовалось возможность проповедовать свои идеи и, более того, претворять своё учение в жизнь, что затруднительно осуществить в Ионии и материковой Элладе, где жило много искушённых в вопросах философии и политики людей. Ямвлих сообщает:
«Его философия распространилась, вся Эллада стала восхищаться им, и лучшие и мудрейшие мужи приезжали к нему на Самос, желая слушать его учение. Сограждане, однако, принуждали его участвовать во всех посольствах и общественных делах. Пифагор чувствовал, как тяжело, подчиняясь законам отечества, одновременно заниматься философией, и видел, что все прежние философы прожили жизнь на чужбине. Обдумав всё это, отойдя от общественных дел и, как говорят некоторые, считая недостаточной невысокую оценку самосцами его учения, он уехал в Италию, считая своим отечеством страну, где больше способных к обучению людей».
Пифагор поселился в греческой колонии Кротоне в Южной Италии, где нашёл много последователей. Их привлекала не только оккультная философия, которую он убедительно излагал, но и предписываемый им образ жизни с элементами здорового аскетизма и строгой морали. Пифагор проповедовал нравственное облагораживание невежественного народа, достигнуть которого возможно там, где власть принадлежит касте мудрых и знающих людей, и которым народ повинуется в чём-то безоговорочно, как дети родителям, а в остальном сознательно, подчиняясь нравственному авторитету. Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя и основателя. Этот орден фактически пришёл в Кротоне к власти, однако из-за антипифагорейских настроений в конце VI в. до н. э. Пифагору пришлось удалиться в другую греческую колонию Метапонт, где он и умер. Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора.
У Пифагора была жена по имени Феано, сын Телавг и дочь.
По Ямвлиху, Пифагор возглавлял своё тайное общество тридцать девять лет, тогда приблизительная дата смерти Пифагора может быть отнесена к 491 до н. э., к началу эпохи греко-персидских войн. Диоген, ссылаясь на Гераклида (IV в. до н. э.), говорит, что Пифагор мирно скончался в возрасте 80 лет, или же в 90 лет (по неназванным другим источникам). Из этого следует дата смерти 490 до н. э. (или 480 до н. э., что маловероятно). Евсевий Кесарийский в своей хронографии обозначил 497 до н. э. как год смерти Пифагора.
Разгром пифагорейского союза
Среди последователей и учеников Пифагора оказалось немало представителей знати, которые пытались изменить законы в своих городах в соответствии с пифагорейским учением. На это наложилась обычная борьба той эпохи между олигархической и демократической партиями в древнегреческом обществе. Недовольство большинства населения, не разделяющего идеалов философа, вылилось в кровавые мятежи в Кротоне и Таренте.
Ямвлих со ссылкой на Аполлония, который пользовался архивами из Кротона, излагает разгром пифагорейцев в Кротоне так:
«Пифагорейцы образовали большое сообщество (их было более трёхсот), но оно составляло лишь небольшую часть города, который уже не управлялся согласно тем же обычаям и нравам. Впрочем, пока кротонцы владели своей землёй, и Пифагор находился у них, сохранялось государственное устройство, существовавшее от основания города, хотя были недовольные, ожидавшие удобного случая для переворота. Но когда завоевали Сибарис, Пифагор уехал, а пифагорейцы, управлявшие завоёванной землёй, не распределили её по жребию, как хотело большинство, то затаённая ненависть вспыхнула, и множество граждан выступило против них… Родственники пифагорейцев относились с ещё большим раздражением к тому, что те подают правую руку только своим, а из близких — только родителям, и что они предоставляют своё имущество для общего пользования, а от имущества родственников оно отделено. Когда родственники начали эту вражду, остальные с готовностью присоединились к конфликту… Через много лет… кротонцами овладели сожаление и раскаяние, и они решили вернуть в город тех пифагорейцев, которые ещё были живы.»
Много пифагорейцев погибло, выжившие рассеялись по Италии и Греции. Немецкий историк Ф. Шлоссер замечает по поводу разгрома пифагорейцев: «Кончилась совершенной неудачей попытка перенести в Грецию кастовый и клерикальный быт и, наперекор духу народа, изменить его политическое устройство и нравы по требованиям отвлечённой теории.»[3]
Согласно Порфирию и сам Пифагор погиб в результате антипифагорейского мятежа в Метапонте, однако другие авторы не подтверждают этой версии, хотя охотно передают историю о том, будто бы удручённый философ уморил себя голодом в священном храме.
Научные достижения
В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»
Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен): «В день, когда Пифагор открыл свой чертёж знаменитый, славную он за него жертву быками воздвиг». Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет. Открытие того факта, что между стороной и диагональю квадрата не существует общей меры, было самой большой заслугой пифагорейцев. Этот факт вызвал первый кризис в истории математики. Пифагорейское учение о целочисленной основе всего существующего больше нельзя было признавать истинным. Поэтому пифагорейцы пытались сохранить своё открытие в тайне и создали легенду о гибели Гиппаса Мессопотамского, который осмелился разгласить открытие. Пифагору приписывают еще ряд важных в то время открытий, а именно: теорему о сумме внутренних углов треугольника; задачу о делении плоскости на правильные многоугольники (треугольники, квадраты и шестиугольники). Есть сведения, что Пифагор построил "космические" фигуры, т. е. пять правильных многогранников. Но вероятнее, что он знал только три простейших правильных многогранника: куб, четырехгранник, восьмигранник. Школа Пифагора много сделала, чтобы придать геометрии характер науки. Основной особенностью метода Пифагора было объединение геометрии с арифметикой. Пифагор много занимался пропорциями и прогрессиями и, вероятно подобием фигур, так как ему приписывают решение задачи: "По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй". Пифагор и его ученики ввели понятие о многоугольных, дружественных, совершенных числах и изучали их свойства. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что "поставил арифметику выше интересов торговца". Пифагор одним из первых считал, что Земля имеет форму шара и является центром Вселенной, что Солнце, Луна и планеты имеют собственное движение, отличное от суточного движения неподвижных звезд. Учение пифагорейцев о движении Земли Николай Коперник воспринял как предысторию своего гелиоцентрического учения. Недаром церковь объявила систему Коперника "ложным пифагорейским учением".
Аристотель затрагивает развитие представлений о космологии в работе «Метафизика», однако вклад Пифагора в ней никак не озвучен. По Аристотелю космологическими теориями занимались пифагорейцы в середине V в. до н. э., но, видимо, не сам Пифагор. Пифагору приписывают открытие, что Земля — шар, но то же открытие наиболее авторитетный автор в этом вопросе, Феофраст, отдаёт Пармениду. Да и Диоген Лаэртский сообщает, что суждение о шарообразности Земли высказывал Анаксимандр Милетский, у которого учился Пифагор в юности. В то же время, научные заслуги школы пифагорейцев в математике и космологии бесспорны. Точку зрения Аристотеля, отражённую в его несохранившемся трактате «О пифагорейцах», передал Ямвлих. По Аристотелю истинными пифагорейцами были акусматики, последователи религиозно-мистического учения о переселении душ. Акусматики рассматривали математику как учение, исходящее не столько от Пифагора, сколько от пифагорейца Гиппаса. В свою очередь математики-пифагорейцы, по их собственному мнению, вдохновлялись направляющим учением Пифагора для углублённого изучения своей науки.
Математика пифагорейцев
Из-за отсутствия документального материала нет возможности установить последовательные этапы дальнейшей двухвековой разработки пифагорейцами математических знаний, первоначально перенятых ими у египтян и вавилонян.
Пифагорейцы изображали числа в виде точек, группируемых в геометрические фигуры. Так возникло понятие «фигурных чисел», в котором нашла свое отражение тесная связь, существующая между понятиями числа и пространственной протяженностью. Например, «квадратные числа» 1, 4, 9 изображались так:
«Треугольные числа» 1, 3, 6 представлялись в таком виде:
У пифагорейцев точка, изображавшая единицу, была дальше неделима – она была математическим атомом; сама точка определялась как единица, обладающая положением. Для того чтобы быть отличимыми друг от друга, единицы-точки должны были отделяться пространством, каждая точка должна была иметь вокруг себя «поле». Благодаря этому каждое число можно было изображать не только при помощи точек, но и квадратных полей, или тех и других, как например, число 3 в виде
Таким образом, в основе здесь лежит понятие числа, которое лишь изображается фигурой: геометрия подчинена арифметике.
Фигурные числа отражали своим видом способ, которым они были арифметически порождены, т. е. были ли они получены путем сложения или умножения. Пифагорейцы и продолжатели их традиций рассматривали преимущественно числа-суммы, между тем Евклид и его школа допускали геометрические изображения лишь для чисел-произведений.
Простейший и древнейший пример арифметического понятия (изображаемого единицами-точками) – это различение четного (парного) и нечетного (непарного). Противоположность нечетного и четного представляет одну из десяти пар противоположностей, считавшихся пифагорейцами философскими категориями.
Числа-произведения делились пифагорейцами на «прямолинейные», т. е. простые числа, которые, так как они не разлагаются на множители, изображались точками, расположенными вдоль отрезка; «плоскостные числа», разлагающиеся на два множителя и изображающиеся точками, образующими прямоугольник или квадрат, и «телесные числа», разлагающиеся на три множителя и изображающиеся точками, образующими параллелепипед или куб.
Среди чисел-сумм пифагорейцы выделяли «многоугольные числа», которые изображались точками, распложенными в виде правильных геометрических тел. Таким образом получали ряды «треугольных», «квадратных», «пятиугольных» и
других «фигурных» чисел. Каждый такой ряд представляет последовательные суммы арифметической прогрессии с разностями 1, 2, 3 и т. д.
На рис. 1.2 изображены «треугольные» числа 1, 1+2=3, 1+2+3=6, 1+2+3+4=10 (общее выражение этих чисел 1+2 +3+... + п= 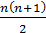 ). ).
Из треугольных чисел пифагорейцы получали и все квадратные числа, способом, который указан на чертеже.
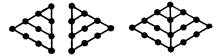
На рис. 1.3 показаны «квадратные» числа 1, 1+3 = 4, 1+3+5=9 (общее выражение этих чисел 1+3+5+..,+(2n – 1) = п2
; наше выражение «квадрат» для числа n2
является пережитком пифагорейской терминологии).
Тем же путем, присоединяя друг к другу три равных треугольных числа, получали пятиугольные числа и т. д. На рис. 1.4 изображены
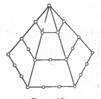 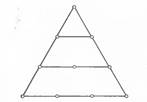 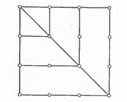
«пятиугольные» числа 1, 1+4=5, (общее выражение этих чисел 1 + 4 + 7 + . . . + (Зn – 2) = 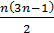 ). ).
кий математик II в. до н. э. Гипсикл показал, что n-е m-угольное число равно  . Пифагорейцы определили также «кубические» числа 1, 8, 27,...(откуда наше выражение «куб» для п3
). . Пифагорейцы определили также «кубические» числа 1, 8, 27,...(откуда наше выражение «куб» для п3
).
Далее определялись «пирамидальные числа», образуемые сложением многоугольных чисел. Простейшие из них, «четырехгранные числа», получаются из треугольных чисел 1 = 1, 1+3 = 4, 1+3 + 6=10, 1+3 + 6+10 = 20... и изображаются в виде пирамид с треугольным основанием. Разумеется, что все фигурные числа и их свойства не были открыты сразу, а постепенно, в течение нескольких веков.
С дальнейшим развитием математики фигурные числа потеряли значение, за одним, однако, исключением: это квадратные и кубические числа, давшие возможность подойти к вычислению площадей и объемов, т. е. к решению собственно геометрических задач. Заменяя единицы-точки полями, мы видим, что квадратные числа, рассматриваемые как числа-суммы, изображаются так:

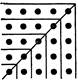
Часть фигуры, соответствующая нечетному числу, от прибавления которого к квадратному числу получается следующее квадратное число, называлась «гномон»: Обозначая первоначально «того, кто знает, различает», затем простейший астрономический инструмент – колышек, перпендикулярный к горизонтальной плоскости (циферблату солнечных часов), образующий прямой угол со своей тенью, – слово «гномон» употреблялось позднее расширительно. Им называли такоеприбавление к геометрической фигуре, которое увеличивает, но не меняет ее (например, гномоном треугольника может оказаться трапеция). Между тем пифагорейцы, исходя из квадрата, отождествляли «гномон» с прямоугольной и обязательно нечетной фигурой.
Рассматривая последовательность гномонов, пифагорейцы извлекали отсюда ряд свойств чисел, например, сумма двух последовательных нечетных чисел равна учетверенному соответствующему (натуральному) числу 1+3=4 1, 3+5=4 1, 3+5=4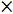 2, 5+7=4 2, 5+7=4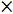 3 и др. В то время как мы легко доказываем эти и подобные свойства, например последнее, при помощи простых алгебраических преобразований (2n–1)+(2n+1)=4n, пифагорейцы лишь проверяли их при помощи наглядной фигуры. 3 и др. В то время как мы легко доказываем эти и подобные свойства, например последнее, при помощи простых алгебраических преобразований (2n–1)+(2n+1)=4n, пифагорейцы лишь проверяли их при помощи наглядной фигуры.
Наряду с квадратными числами большое значение у пифагорейцев имели «продолговатые числа» – числа вида п(п+1). Разумеется, что число, принадлежащее одной категории, могло вместе с тем принадлежать и другой. Пифагорейцы знали также «подобные числа», например, 6=2´3, 24=4´6, 54=6´9, изображаемые прямоугольниками с пропорциональными сторонами. Эти числа обладают рядом интересных свойств: например, произведение двух «подобных чисел» является «квадратным числом».
Изучение чисел-сумм, изображаемых фигурами, составленными из единиц-точек, послужило основанием для суммирования числовых рядов, которым успешно занимался Архимед. Изучение «прямолинейных чисел» дало толчок к возникновению теории простых чисел, важные результаты которой были получены Евклидом, использовавшим в теоретико-числовых книгах своих «Начал» многие понятия, введенные пифагорейцами.
Различая, кроме простых чисел, составные и взаимно простые (первые между собой, т. е. не имеющие общего делителя, например, 14 и 55), пифагорейцы, и, с некоторыми отклонениями, греческие математики, вообще уделяли также много внимания дальнейшей классификации четных и нечетных чисел, различая (как позже Евклид) четно-четные, четно-нечетные, нечетно-нечетные и т. п. числа. При этом соблюдавшие пифагорейскую традицию не включали в нечетные числа, да и в числа вообще, 1, а в четные – 2, считая их «началами» чисел и помещая вне ряда чисел.
Пифагорейцы занимались также вопросом об отношении чисел к сумме своих делителей. Под делителями числа понимались все его делители, простые и составные, включая 1, но исключая само число. Если сумма делителей оказывалась больше самого данного числа, то число называли «сверхсовершенным», если она была равна ему – «совершенным», а если меньше его – «недостающим».
Наконец, пифагорейцами рассматривались «дружественные числа», т. е. такиеНаконец, пифагорейцами рассматривались «дружественные числа», т. е. такие два числа, каждое из которых равно сумме делителей другого. Неоплатоник сириец Ямблих (около 250–325 гг. н. э.) приписывает Пифагору открытие дружественных чисел 220 и 284, единственной пары, известной в древности. В Средние века считали, что талисманы с дружественными числами способны укрепить близость между людьми. Арабский математик Сабит ибн Корра (826–901 гг.) нашел правило образования дружественных чисел, которое было забыто и вновь открыто Ферма и опубликовано (без доказательства) Декартом (1638 г.).
Пифагорейцы исследовали неопределенное уравнение x2
+y2
=z2
, целые решения которого поэтому называют «пифагоровыми тройками», и нашли бесконечно много таких троек, имеющих вид
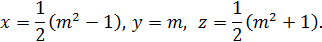
Правила, которые мы записываем формулами
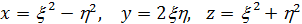
и которые охватывают всю совокупность решений этого уравнения, встречаются у Диофанта, но должны были быть известны задолго до него.
Ранние пифагорейцы связывали с целыми числами и различные мистические спекуляции. Так, особенно совершенным представилось им число 10 – декада, так как 10 = 1 + 2 + 3 + 4, но 1 есть единица (монада), Матерь всех чисел, 2 выражает линию, 3 – треугольник, а 4 – пирамиду. Это древнее рассуждение замечательно тем, что числа 2, 3 и 4 связываются с размерностью геометрических образов. Две точки определяют прямую – это одномерный образ, три точки (не лежащие на одной прямой) – треугольник или плоскость – двумерный образ; наконец, 4 точки (не лежащие в одной плоскости) – пирамиду – трехмерный образ. Кроме того, среди чисел, меньших 10, столько же простых, сколько составных, и т. д. Исходя из замечательных свойств декады, пифагорейцы считали, что число небесных сфер должно быть равно 10, а так как их насчитывали только 9 (сферы неба, Солнца, Луны, Земли, Меркурия, Венеры, Марса, Юпитера и Сатурна), то была придумана новая планета – Противоземлие, которая вращалась по десятой сфере. Аналогичные мистические спекуляции с числами были распространены и среди ученых XV–XVI вв., и вообще они характерны для ранних стадий развития науки.
АРХИМЕД (около 287 до н.э.— 212 до н.э.)
Биография
Архимед (около 287 до н.э.— 212 до н.э.), родился в 287 году до нашей эры в греческом городе Сиракузы, расположенного на восточном побережье острова Сицилии, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. В теоретическом отношении труд этого великого ученого был ослепляюще многогранным. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики.
Если ко всему перечисленному прибавить еще то, что сделано Архимедом в области механики, то станут понятными то изумление и уважение, с которыми к нему относились его современники и теперь относятся все те, кто близок к математике, механике и прикладным наукам.
Пленяет и высокий моральный облик Архимеда. Он был подлинным патриотом своего города. Когда настали тяжелые дни для Сиракуз и римские войска под командованием Марцелла осадили город с двух сторон и никто из осажденных уже не надеялся на спасение, вот тут-то и привел Архимед в действие свои машины, которые задолго до этого он построил.
«В неприятельскую пехоту неслись пущенные им раз личного рода стрелы и невероятной величины камни с шумом и страшной быстротой. Решительно ничто не могло вынести силы их удара; они опрокидывали тех, в кого они попадали, и расстраивали их ряды. На море внезапно поднимались со стен над кораблями бревна, загнутые наподобие рога. Одни из них ударяли в некоторые корабли сверху и силой удара топили их; другие железными лапами или клювами, наподобие журавлиных, схватывали корабли за носы, поднимали их на воздух, ставили корабль на корму и затем топили. Часто корабль поднимало высоко над поверхностью моря, и, вися в воздухе, он к ужасу окружающих качался в разные стороны, являя собой страшное зрелище, пока весь экипаж не был сброшен или перестрелян. Самбука, машина, которую Марцелл поставил на несколько кораблей и подводил к стенам еще далеко не успела подойти к ним, как из-за них вылетел камень весом в десять талантов, за ним другой, третий... Они падали на машину со страшным шумом и силой, разбили ее корпус, разорвали болты и уничтожили связи, так что Марцелл, не зная что делать, решил отплыть поспешно с флотом и приказал пехоте отступать, но стрелы и здесь настигали их, попадали в отступающих, так что они понесли большие потери. Марцелл все же успел избежать опасности. Он шутил над своими техниками и механиками и говорил: «Уж не перестать ли нам драться с математиком? Он, сидя спокойно за стеной, топит наши корабли и, бросая в нас разом столько стрел, оставляет позади мифических сторуких великанов. Действительно, все остальные сиракузяне служили своего рода телом архимедовых машин, один он был душой, которая всех двигала, все направ ляла» (Плутарх).
Машины Архимеда могли защитить город только от неприятельских приступов, но не могли спасти осажденных от голода. Марцеллу удалось, наконец, ворваться в город. Взятие Сиракуз, как и других городов, попавших в руки римлян, сопровождалось невероятными актами жестокости, убийствами и грабежами. В числе убитых был и Архимед.
Рассказ о смерти Архимеда существует в нескольких версиях.
1. Рассказ Иоанна Цеца (Chiliad, книга II): в разгар боя 75-летний Архимед сидел на пороге своего дома, углублённо размышляя над чертежами, сделанными им прямо на дорожном песке. В это время пробегавший мимо римский воин наступил на чертёж, и возмущённый ученый бросился на римлянина с криком: «Не тронь моих чертежей!» Солдат остановился и хладнокровно зарубил старика мечом.
2. Рассказ Плутхара: «К Архимеду подошёл солдат и объявил, что его зовёт Марцелл. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешённой. Солдат, которому не было дела до его доказательства, рассердился и пронзил его своим мечом». Плутарх утверждает, что генерал Марцелл был разгневан гибелью Архимеда, которого он якобы приказал не трогать.
3. Воин ворвался в дом Архимеда для грабежа, занёс меч на хозяина, а тот только и успел крикнуть: «Остановись, подожди хотя бы немного. Я хочу закончить решение задачи, а потом делай что хочешь!»
4. Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что учёный несёт в ларце золото или драгоценности, и, недолго думая, перерезали ему горло.
Таковы легенды. Однако многие историки полагают, что Архимед был убит не случайно – ведь его ум стоил в те времена целой армии.
Цицерон, бывший квестором на Сицилии в 75 году до н. э., пишет в «Тускуланских беседах» (книга V), что ему в 75 году до н. э., спустя 137 лет после этих событий, удалось обнаружить полуразрушенную могилу Архимеда; на ней, как и завещал Архимед, было изображение шара, вписанного в цилиндр.
Легенды
Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том, как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота или ювелир подмешал туда значительное количество серебра. Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объём короны: ведь она имела неправильную форму! Архимед всё время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить её объём, измерив объём вытесненной ею воды. Согласно легенде, Архимед выскочил голый на улицу с криком «Эврика!» (εύρηκα), то есть «Нашёл!». В этот момент был открыт основной закон гидростатики: закон Архимеда.
Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею тяжёлый многопалубный корабль «Сиракузия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. По легенде, Архимед заявил при этом: «Будь в моём распоряжении другая Земля, на которую можно было бы встать, я сдвинул бы с места нашу» (в другом варианте: «Дайте мне точку опоры, и я сдвину Землю»).
Научная деятельность
По словам Плутарха, Архимед был просто одержим математикой. Он забывал о пище, совершенно не заботился о себе.
Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида 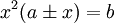 , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать. , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. Идеи Архимеда легли впоследствии в основу интегрального исчисления.
Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3.
Лучшим своим достижением он считал определение поверхности и объёма шара – задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.
В сочинении Квадратура параболы Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 4/3 от площади вписанного в этот сегмент треугольника (см. рисунок).
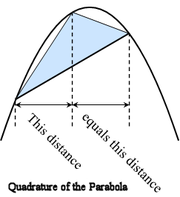
Рис. 2.3 – Квадратура сегмента параболы
Для доказательства Архимед подсчитал сумму бесконечного ряда:
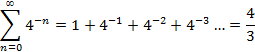
Каждое слагаемое ряда – это общая площадь треугольников, вписанных в неохваченную предыдущими членами ряда часть сегмента параболы.
Следующая задача относится к геометрии кривых. Пусть дана некоторая кривая линия. Как определить касательную в любой её точке? Или, если переложить эту проблему на язык физики, пусть нам известен путь некоторого тела в каждый момент времени. Как определить скорость его в любой точке? В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод впоследствии лёг в основу дифференциального исчисления.
В математике, физике и астрономии очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин – их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами определения касательных и показал, как решать задачи на экстремумы.
Задача о трисекции угла
Задача о делении угла на три равные части возникла из потребностей архитектуры и строительной техники. При составлении рабочих чертежей, разного рода украшений, многогранных колоннад, при строительстве, внутренней и внешней отделки храмов, надгробных памятников древние инженеры, художники встретились с необходимостью уметь делить окружность на три равные части, а это часто вызывало затруднения. Оригинальное и вместе с тем чрезвычайно простое решение задачи о трисекции угла дал Архимед.
Измерение круга
Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру.
Задача о квадратуре круга заключается в следующем: построить квадрат, площадь которого была бы равна площади данного круга. Большой вклад в решение этой задачи внес Архимед. В своем трактате "Измерение круга" он доказывает следующие три теоремы:
Теорема первая: Площадь круга равна площади прямоугольного треугольника, один из катетов которого равняется длине окружности круга, а другой радиусу круга.
Теорема вторая: Площадь круга относится к площади квадрата, построенного на диаметре, приблизительно, как 11:14.
Теорема третья: C-3d < d и C-3d > d, где С -длина окружности, а d-ее диаметр. Откуда, d < C-3d < d. Верхнюю и нижнюю границы для числа Архимед получил путем последовательного рассмотрения отношений периметров к диаметру правильных описанных и вписанных в круг многоугольников, начиная с шестиугольника и кончая 96-угольником. Если приравнять верхней границе, то получим архимедово значение (архимедова постоянная равная 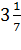 ). Более того, Архимед сумел оценить точность приближения для числа π: ). Более того, Архимед сумел оценить точность приближения для числа π: 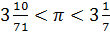 . .
Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел. Некоторые теоремы планиметрии также впервые были доказаны Архимедом. Так, теорема о площади треугольника по трем его сторонам 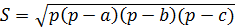 указанную формулу называют формулой Герона, потому что ему принадлежит заслуга широкого применения её на практике. Приписываемая Герону, впервые была предложена Архимедом.Математический метод Архимеда, связанный с математическими работами пифагорейцев и с завершившей их работой Эвклида, а также с открытиями современников Архимеда, подводил к познанию материального пространства, окружающего нас, к познанию теоретической формы предметов, находящихся в этом пространстве, формы совершенной, геометрической формы, к которой предметы более или менее приближаются и законы которой необходимо знать, если мы хотим воздействовать на материальный мир. Но Архимед знал также, что предметы имеют не только форму и измерение: они движутся, или могут двигаться, или остаются неподвижными под действием определенных сил, которые двигают предметы вперед или приводят в равновесие. Великий сиракузец изучал эти силы, изобретая новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, это статика, а также гидростатика. указанную формулу называют формулой Герона, потому что ему принадлежит заслуга широкого применения её на практике. Приписываемая Герону, впервые была предложена Архимедом.Математический метод Архимеда, связанный с математическими работами пифагорейцев и с завершившей их работой Эвклида, а также с открытиями современников Архимеда, подводил к познанию материального пространства, окружающего нас, к познанию теоретической формы предметов, находящихся в этом пространстве, формы совершенной, геометрической формы, к которой предметы более или менее приближаются и законы которой необходимо знать, если мы хотим воздействовать на материальный мир. Но Архимед знал также, что предметы имеют не только форму и измерение: они движутся, или могут двигаться, или остаются неподвижными под действием определенных сил, которые двигают предметы вперед или приводят в равновесие. Великий сиракузец изучал эти силы, изобретая новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, это статика, а также гидростатика.Спираль Архимеда
Архимедова спираль описывается точкой M, движущейся равномерно по прямой d, которая вращается вокруг точки O, принадлежащей этой прямой. В начальный момент движения M совпадает с центром вращения O прямой. Площадь сектора, ограничиваемого дугой архимедовой спирали и двумя радиус-векторами и соответствующими углами.
Инфинитезимальные методы
В группу инфинитезимальных методов входят: метод исчерпывания, метод интегральных сумм, дифференциальные методы. Одним из самых ранних методов является метод интегральных сумм. Он применялся при вычислении площадей фигур, объемов тел, длин кривых линий. Для вычисления объема, тело вращения разбивается на части, и каждая часть аппроксимируется (приближается) описанными и вписанными телами, объемы которых можно вычислить. Теперь остается выбрать аппроксимирующие сверху и снизу тела таким образом, чтобы разность их объемов могла быть сделана сколь угодно малой.
Дифференциальным методом Архимед находил касательную к спирали. Идеи Архимеда почти на два тысячелетия опередили своё время. Только в XVII веке учёные смогли продолжить и развить труды великого греческого математика.
В честь Архимеда названы кратер Archimedes и горная цепь MontesArchimedes; астероид 3600 Архимед. Лейбниц писал: «Внимательно читая сочинения Архимеда, перестаёшь удивляться всем новым открытиям геометров». В честь Архимеда названы улицы в Донецке, Днепропетровске, Нижнем Новгороде и Амстердаме, площадь в Сиракузах.
Сочинения
До наших дней сохранились:
· Квадратура параболы / τετραγωνισμὸς παραβολῆς— определяется площадь сегмента параболы.
· О шаре и цилиндре / περὶ σφαίρας καὶ κυλίνδρου— доказывается, что объём шара равен 2/3 от объёма, описанного около него цилиндра, а площадь поверхности шара равна площади боковой поверхности этого цилиндра.
· О спиралях / περὶἑλίκων— выводятся свойства спирали Архимеда.
· О коноидах и сфероидах / περὶ κωνοειδέων καὶ σφαιροειδέων— определяются объёмы сегментов параболоидов, гиперболоидов и эллипсоидов вращения.
· О равновесии плоских фигур / περὶἰσορροπιῶν— выводится закон равновесия рычага; доказывается, что центр тяжести плоского треугольника находится в точке пересечения его медиан; находятся центры тяжести параллелограмма, трапеции и параболического сегмента.
· Послание к Эратосфену о методе / πρὸς Ἐρατοσθένην ἔφοδος— обнаружено в 1906 году, по тематике частично дублирует работу «О шаре и цилиндре», но здесь используется механический метод доказательства математических теорем.
· О плавающих телах / περὶ τῶν ὀχουμένων— выводится закон плавания тел; рассматривается задача о равновесии сечения параболоида, моделирующего корабельный корпус.
· Измерение круга / κύκλου μέτρησις— до нас дошёл только отрывок из этого сочинения. Именно в нём Архимед вычисляет приближение для числа π.
· Псаммит / ψαμμίτης— вводится способ записи очень больших чисел.
· Стомахион / στομάχιον— дано описание популярной игры.
· Задача Архимеда о быках / πρόβλημα βοικόν— ставится задача, приводимая к уравнению Пелля.
Ряд работ Архимеда сохранился только в арабском переводе:
· Трактат о построении около шара телесной фигуры с четырнадцатью основаниями;
· Книга лемм;
· Книга о построении круга, разделённого на семь равных частей;
· Книга о касающихся кругах.
|