Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедройШеметков Л.А.
«2008 г.
Тригонометрические уравнения и неравенства
Курсовая работа
Исполнитель:
студент группы М-51
С.М. Горский
Научный руководительк.ф.- м.н.,
старший преподаватель
В.Г. Сафонов
Гомель 2008
Оглавление
ВВЕДЕНИЕ
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Элементарные тригонометрические уравнения
Введение вспомогательного аргумента
Схема решения тригонометрических уравнений
Преобразование и объединение групп общих решений тригонометрических уравнений
Разложение на множители
Решение уравнений преобразованием произведения тригонометрических функций в сумму
Решение уравнений с применением формул понижения степени
Решение уравнений с применением формул тройного аргумента
Равенство одноименных тригонометрических функций
Домножение на некоторую тригонометрическую функцию
Сведение тригонометрических уравнений к алгебраическим
НЕСТАНДАРТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Использование ограниченности функций
Функциональные методы решения тригонометрических и комбинированных уравнений
Решение с исследованием функции
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Решение тригонометрических неравенств с помощью единичной окружности
Решение тригонометрических неравенств графическим методом
ОТБОР КОРНЕЙ
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом <<исчисление хорд>>. Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции.
Тригонометрические уравнения одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий централизованного тестирования.
Реклама

Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях конечное число корней, а в тригонометрических --- бесконечное, что сильно усложняет отбор корней. Еще одной спецификой тригонометрических уравнений является неединственность формы записи ответа.
Данная дипломная работа посвящена методам решения тригонометрических уравнений и неравенств.
Дипломная работа состоит из 6 разделов.
В первом разделе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; таблица значений тригонометрических функций для некоторых аргументов; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции.
Во втором разделе изложены основные методы решения тригонометрических уравнений. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, что может <<сбить с толку>> при решении тестов, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений.
В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе.
В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов.
В пятом разделе представлены наиболее сложные задания: когда необходимо не только решить тригонометрическое уравнение, но и из найденных корней отобрать корни, удовлетворяющие какому-нибудь условию. В данном разделе приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
Реклама

В шестом разделе представлены задачи для самостоятельного решения, оформленные в виде теста. В 20 заданиях теста приведены наиболее сложные задания, которые могут встретиться на централизованном тестировании.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Элементарные тригонометрические уравнения --- это уравнения вида 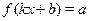 , где , где 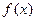 --- одна из тригонометрических функций: --- одна из тригонометрических функций: 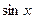 , , 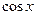 , , 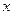 , , 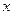 . .
Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению 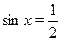 удовлетворяют следующие значения: удовлетворяют следующие значения: 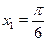 , , 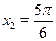 , , 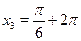 , , 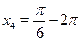 и т. д. Общая формула по которой находятся все корни уравнения и т. д. Общая формула по которой находятся все корни уравнения 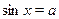 , где , где 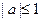 , такова: , такова:
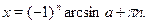
Здесь 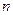 может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения) может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения) 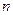 называют параметром
. Записывают обычно называют параметром
. Записывают обычно 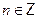 , подчеркивая тем самым, что параметр , подчеркивая тем самым, что параметр 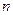 принимать любые целые значения. принимать любые целые значения.
Решения уравнения 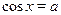 , где , где 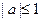 , находятся по формуле , находятся по формуле
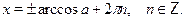
Уравнение 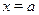 решается применяя формулу решается применяя формулу
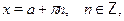
а уравнение 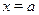 --- по формуле --- по формуле
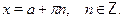
Особо отметим некоторые частные случаи элементраных тригонометрических уравнений, когда решение может быть записано без применения общих формул:
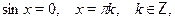
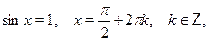
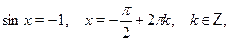
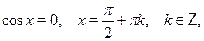
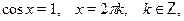
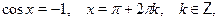
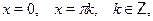
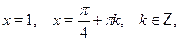
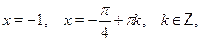
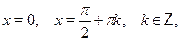
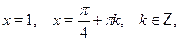
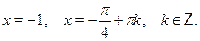
При решении тригонометрических уравнений важную роль играет период тригонометрических функций. Поэтому приведем две полезные теоремы:
Теорема
Если 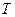 --- основной период функции --- основной период функции 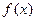 , то число , то число  является основным периодом функции является основным периодом функции 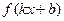 . .
Периоды функций 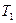 и и 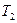 называются соизмеримыми, если существуют натуральные числа называются соизмеримыми, если существуют натуральные числа 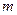 и и 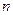 , что , что 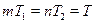 . .
Теорема
Если периодические функции 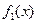 и и 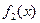 , имеют соизмеримые , имеют соизмеримые 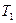 и и 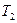 , то они имеют общий период , то они имеют общий период 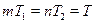 , который является периодом функций , который является периодом функций 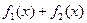 , , 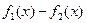 , , 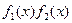 . .
В теореме говорится о том, что 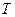 является периодом функции является периодом функции 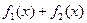 , , 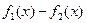 , , 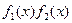 , и не обязательно является основным периодом. Например, основной период функций , и не обязательно является основным периодом. Например, основной период функций 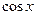 и и 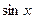 --- --- 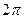 , а основной период их произведения --- , а основной период их произведения --- 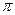 . .
Стандартным путем преобразования выражений вида 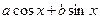 является следующий прием: пусть является следующий прием: пусть 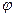 --- угол, задаваемый равенствами --- угол, задаваемый равенствами 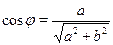 , , 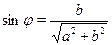 . Для любых . Для любых 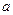 и и 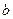 такой угол существует. Таким образом такой угол существует. Таким образом 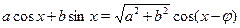 . Если . Если 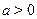 , , 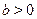 или или 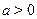 , , 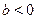 , , 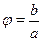 , в других случаях , в других случаях 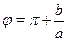 . .
Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений следующая:
решение заданного уравнения сводится к решению элементарных уравнений. Средства решения --- преобразования, разложения на множители, замена неизвестных. Ведущий принцип --- не терять корней. Это означает, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей "цепочки" (или совокупность уравнений в случае ветвления) являлось следствием предыдущего. Одним из возможных методов отбора корней является проверка. Сразу заметим, что в случае тригонометрических уравнений трудности, связанные с отбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями. Ведь проверять приходится серии, состоящие из бесконечного числа членов.
Особо следует сказать о замене неизвестных при решении тригонометрических уравнений. В большинстве случаев после нужной замены получается алгебраическое уравнение. Более того, не так уж и редки уравнения, которые, хотя и являются тригонометрическими по внешнему виду, по существу таковыми не являются, поскольку уже после первого шага --- замены переменных --- превращаются в алгебраические, а возращение к тригонометрии происходит лишь на этапе решения элементарных тригонометрических уравнений.
Еще раз напомним: замену неизвестного следует делать при первой возможности, получившееся после замены уравнение необходимо решить до конца, включая этап отбора корней, а уж затем возвратится к первоначальному неизвестному.
Одна из особенностей тригонометрических уравнений заключается в том, что ответ во многих случаях может быть записан различными способами. Даже для решения уравнения 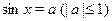 ответ может быть записан следующим образом: ответ может быть записан следующим образом:
1) в виде двух серий: 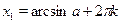 , , 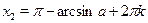 , , 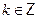 ; ;
2) в стандартной форме представляющей собой объединение указанных выше серий: 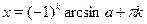 , , 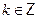 ; ;
3) поскольку 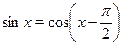 , то ответ можно записать в виде , то ответ можно записать в виде 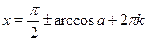 , , 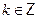 . (В дальнейшем наличие параметра . (В дальнейшем наличие параметра 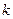 , , 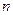 , , 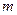 или или 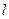 в записи ответа автоматически означает, что этот параметр принимает всевозможные целочисленные значения. Исключения будут оговариваться.) в записи ответа автоматически означает, что этот параметр принимает всевозможные целочисленные значения. Исключения будут оговариваться.)
Очевидно, что тремя перечисленными случаями не исчерпываются все возможности для записи ответа рассматриваемого уравнения (их бесконечно много).
Например, при 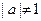 справедливо равенство справедливо равенство 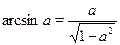 . Следовательно, в двух первых случаях, если . Следовательно, в двух первых случаях, если 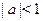 , мы можем заменить , мы можем заменить 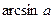 на на 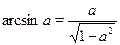 . .
Обычно ответ записывается на основании пункта 2. Полезно запомнить следующую рекомендацию: если на решении уравнения 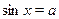 работа не заканчивается, необходимо еще провести исследование, отбор корней, то наиболее удобна форма записи, указанная в пункте 1. (Аналогичную рекомендацию следует дать и для уравнения работа не заканчивается, необходимо еще провести исследование, отбор корней, то наиболее удобна форма записи, указанная в пункте 1. (Аналогичную рекомендацию следует дать и для уравнения 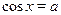 .) .)
Рассмотрим пример иллюстрирующий сказанное.
Пример
Решить уравнение 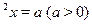 . .
Решение.
Наиболее очевидным является следующий путь. Данное уравнение распадается на два: 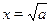 и и 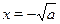 . Решая каждое из них и объединяя полученные ответы, найдем . Решая каждое из них и объединяя полученные ответы, найдем 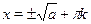 . .
Другой путь.
Поскольку 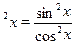 , то, заменяя , то, заменяя 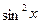 и и 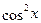 по формулам понижения степени. После небольших преобразований получим по формулам понижения степени. После небольших преобразований получим 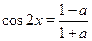 , откуда , откуда 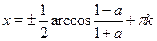 . .
На первый взгляд никаких особых преимуществ у второй формулы по сравнению с первой нет. Однако, если возьмем, например, 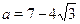 , то окажется, что , то окажется, что 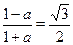 , т.е. уравнение , т.е. уравнение 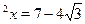 имеет решение имеет решение 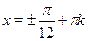 , в то время как первый способ нас приводит к ответу , в то время как первый способ нас приводит к ответу 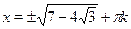 . "Увидеть" и доказать равенство . "Увидеть" и доказать равенство 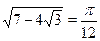 не так просто. не так просто.
Ответ.
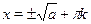 . .
Будем рассматривать арифметическую прогрессию, бесконечно простирающуюся в обе стороны. Члены этой прогресссии можно разбить на две группы членов, располагающиеся вправо и влево от некоторого члена, называемого центральным или нулевым членом прогрессии.
Фиксируя один из членов бесконечной прогрессиии нулевым номером, мы должны будем вести двойную нумерацию для всех оставшихся членов: положительную для членов, расположенных вправо, и отрицательную для членов, расположенных влево от нулевого.
В общем случае, если разность прогрессии 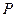 , нулевой член , нулевой член 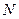 , формула для любого ( , формула для любого (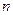 -го) члена бесконечной арифметической прогрессии представляет вид: -го) члена бесконечной арифметической прогрессии представляет вид:
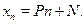
Преобразования формулы для любого члена бесконечной арифметической прогрессии
1. Если к нулевому члену 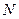 прибавить или отнять разность прогрессии прибавить или отнять разность прогрессии 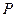 , то от этого прогрессия не изменится, а только переместится нулевой член, т.е. изменится нумерация членов. , то от этого прогрессия не изменится, а только переместится нулевой член, т.е. изменится нумерация членов.
2. Если коэффициент при переменной величине 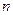 умножить на умножить на 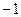 , то от этого произойдет лишь перестановка правой и левой групп членов. , то от этого произойдет лишь перестановка правой и левой групп членов.
3. Если 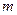 последовательных членов бесконечной прогрессии последовательных членов бесконечной прогрессии
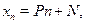
например 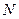 , , 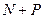 , , 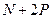 , ..., , ..., 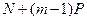 , сделать центральными членами , сделать центральными членами 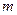 прогрессий с одинаковой разностью, равной прогрессий с одинаковой разностью, равной 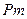 : :

то прогрессия и ряд прогрессий выражают собой одни и те же числа.
Пример
Ряд 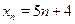 может быть заменен следующими тремя рядами: может быть заменен следующими тремя рядами: 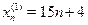 , , 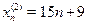 , , 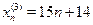 . .
4. Если 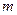 бесконечных прогрессий с одинаковой разностью бесконечных прогрессий с одинаковой разностью 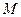 имеют центральными членами числа, образующие арифметическую прогрессию с разностью имеют центральными членами числа, образующие арифметическую прогрессию с разностью 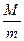 , то эти , то эти 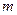 рядов могут быть заменены одной прогрессией с разностью рядов могут быть заменены одной прогрессией с разностью 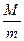 , и с центральным членом, равным любому из центральных членов данных прогрессий, т.е. если , и с центральным членом, равным любому из центральных членов данных прогрессий, т.е. если

то эти 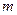 прогрессий объединяются в одну: прогрессий объединяются в одну: 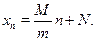
Пример
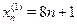 , , 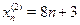 , , 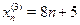 , , 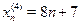 обе объединяются в одну группу обе объединяются в одну группу 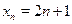 , так как , так как 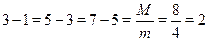 . .
Для преобразования групп, имеющих общие решения, в группы, общих решений не имеющие данные группы разлагают на группы с общим периодом, а затем стремяться объединить получившиеся группы, исключив повторяющиеся.
Метод разложения на множетели заключается в следующем: если
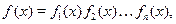
то всякое решение уравнения
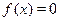
является решение совокупности уравнений
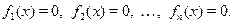
Обратное утверждение, вообще говоря неверно: не всякое решение совокупности является решением уравнения. Это объясняется тем, что решения отдельных уравнений могут не входить в область определения функции 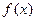 . .
Пример
Решить уравнение 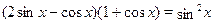 . .
Решение.
Используя основное тригонометрическое тождество, уравнение представим в виде 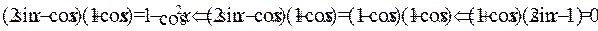
Ответ.
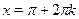 ; ; 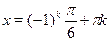 . .
Преобразование суммы тригонометрических функций в произведение
Пример
Решить уравнение 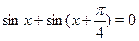 . .
Решение.
Применим формулу , получим равносильное уравнение
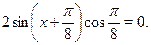
Ответ.
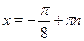 . .
Пример
Решить уравнение 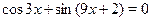 . .
Решение.
В данном случае, прежде чем применять формулы суммы тригонометрических функций, следует использовать формулу приведения 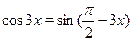 . В итоге получим равносильное уравнение . В итоге получим равносильное уравнение
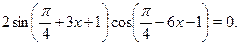
Ответ.
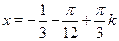 , , 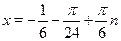 . .
При решении ряда уравнений применяются формулы.
Пример
Решить уравнение 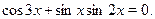
Решение.
Применив формулу , получим равносильное уравнение:
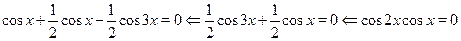
Ответ.
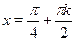 , , 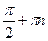 . .
Пример
Решить уравнение 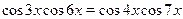 . .
Решение.
Применив формулу , получим равносильное уравнение:
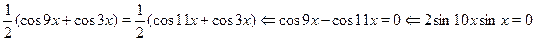 . .
Ответ.
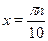 . .
При решении широкого круга тригонометрических уравнений ключевую роль играют формулы.
Пример
Решить уравнение 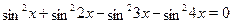 . .
Решение.
Применяя формулу, получим равносильное уравнение.
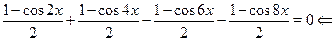

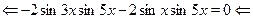
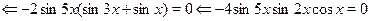 . .
Ответ.
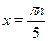 ; ; 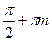 . .
Пример
Решить уравнение 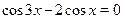 . .
Решение.
Применим формулу , получим уравнение
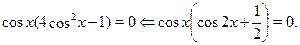
Ответ.
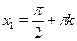 ; ; 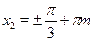 . .
Пример
Решить уравнение 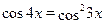 . .
Решение.
Применим формулы понижения степени получим: 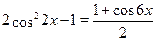 . Применяя получаем: . Применяя получаем:
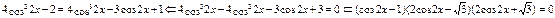 . .
Ответ.
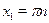 ; ; 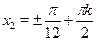 . .
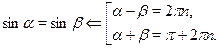
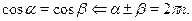
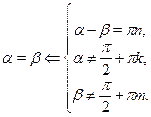
Пример
Решить уравнение 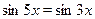 . .
Решение.
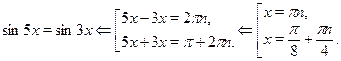
Ответ.
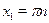 , , 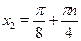 . .
Пример
Решить уравнение 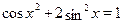 . .
Решение.
Преобразуем уравнение. 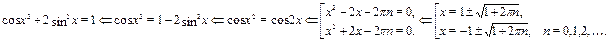
Ответ.
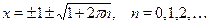 . .
Пример
Известно, что 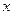 и и 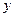 удовлетворяют уравнению удовлетворяют уравнению
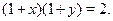
Найти сумму 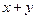 . .
Решение.
Из уравнения следует, что
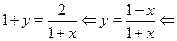
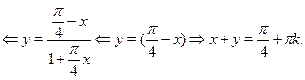
Ответ.
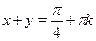 . .
Домножение на некоторую тригонометрическую функцию
Рассмотрим суммы вида
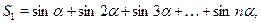
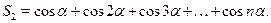
Данные суммы можно преобразовать в произведение, домножив и разделив их на 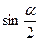 , тогда получим , тогда получим
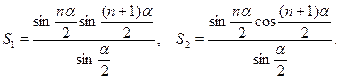
Указанный прием может быть использован при решении некоторых тригонометрических уравнений, однако следует иметь в виду, что в результате возможно появление посторонних корней. Приведем обобщение данных формул:
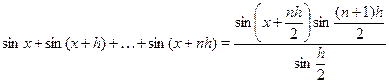
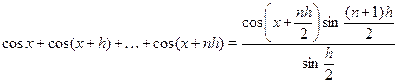
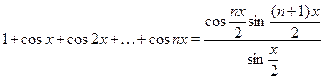
Пример
Решить уравнение 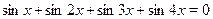 . .
Решение.
Видно, что множество 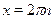 является решением исходного уравнения. Поэтому умножение левой и правой части уравнения на является решением исходного уравнения. Поэтому умножение левой и правой части уравнения на 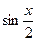 не приведет к появлению лишних корней. не приведет к появлению лишних корней.
Имеем 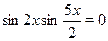 . .
Ответ.
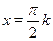 ; ; 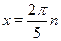 . .
Пример
Решить уравнение 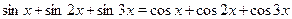 . .
Решение.
Домножим левую и правую части уравнения на 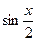 и применив формулы преобразования произведения тригонометрических функций в сумму, пролучим и применив формулы преобразования произведения тригонометрических функций в сумму, пролучим
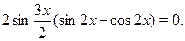
Это уравнение равносильно совокупности двух уравнений 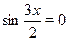 и и 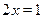 , откуда , откуда 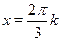 и и 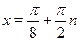 . .
Так как корни уравнения 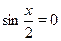 не являются корнями уравнения, то из полученных множеств решений следует исключить не являются корнями уравнения, то из полученных множеств решений следует исключить 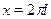 . Значит во множестве . Значит во множестве 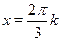 нужно исключить нужно исключить 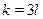 . .
Ответ.
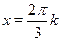 и и 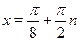 , , 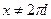 . .
Пример
Решить уравнение 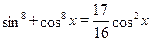 . .
Решение.
Преобразуем выражение 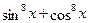 : :
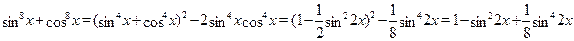
Уравнение запишется в виде:
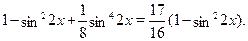
Принимая 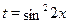 , получаем , получаем 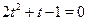 . . 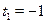 , , 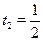 . Следовательно . Следовательно
Ответ.
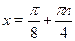 . .
Сводящиеся к квадратным
Если уравнение имеет вид
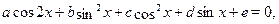
то замена 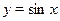 приводит его к квадратному, поскольку приводит его к квадратному, поскольку 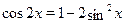 () и . () и .
Если вместо слагаемого 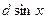 будет будет 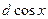 , то нужная замена будет , то нужная замена будет 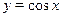 . .
Уравнение
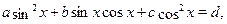
сводится к квадратному уравнению
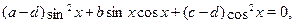
представлением 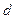 как как 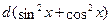 . Легко проверить, что . Легко проверить, что 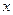 при которых при которых 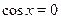 , не являются корнями уравнения, и, сделав замену , не являются корнями уравнения, и, сделав замену 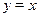 , уравнение сводится к квадратному. , уравнение сводится к квадратному.
Пример
Решить уравнение 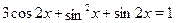 . .
Решение.
Перенесем 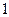 в левую часть, заменим ее на в левую часть, заменим ее на 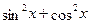 , , 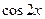 и и 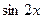 выразим через выразим через 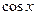 и и 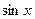 . .
После упрощений получим: 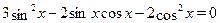 . Разделим почленно на . Разделим почленно на 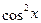 , сделаем замену , сделаем замену 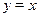 : :
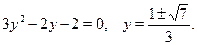
Возвращаясь к 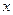 , найдем , найдем 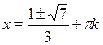 . .
Уравнения, однородные относительно 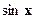 , , 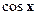
Рассмотрим уравнение вида
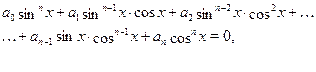
где 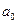 , , 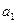 , , 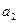 , ..., , ..., 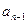 , , 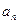 --- действительные числа. В каждом слагаемом левой части уравнения степени одночленов равны --- действительные числа. В каждом слагаемом левой части уравнения степени одночленов равны 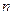 , т. е. сумма степеней синуса и косинуса одна и та же и равна , т. е. сумма степеней синуса и косинуса одна и та же и равна 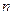 . Такое уравнение называется однородным
относительно . Такое уравнение называется однородным
относительно 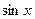 и и 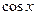 , а число , а число 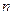 называется показателем однородности
. называется показателем однородности
.
Ясно, что если 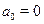 , то уравнение примет вид: , то уравнение примет вид:
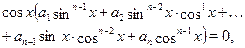
решениями которого являются значения 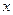 , при которых , при которых 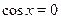 , т. е. числа , т. е. числа 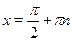 , , 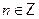 . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже. . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же 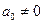 , то эти числа не являются корнями уравнения . , то эти числа не являются корнями уравнения .
При 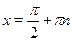 получим: получим: 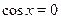 , , 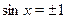 и левая часть уравнения (1) принимает значение и левая часть уравнения (1) принимает значение 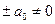 . .
Итак, при 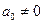 , ,  и и 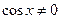 , поэтому можно разделить обе части уравнения на , поэтому можно разделить обе части уравнения на  . В результате получаем уравнение: . В результате получаем уравнение:
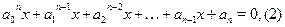
которое, подстановкой 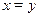 легко сводится к алгебраическому: легко сводится к алгебраическому:
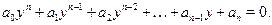
Однородные уравнения с показателем однородности 1. При 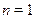 имеем уравнение имеем уравнение 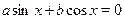 . .
Если 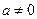 , то это уравнение равносильно уравнению , то это уравнение равносильно уравнению 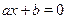 , , 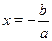 , откуда , откуда 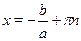 , , 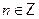 . .
Пример
Решите уравнение 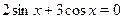 . .
Решение.
Это уравнение однородное первой степени 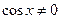 . Разделим обе его части на . Разделим обе его части на 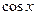 получим: получим:  , , 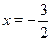 , , 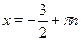 , , 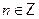 . .
Ответ.
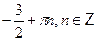 . .
Пример
При 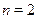 получим однородное уравнение вида получим однородное уравнение вида
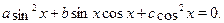
Решение.
Если 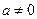 , тогда разделим обе части уравнения на , тогда разделим обе части уравнения на 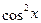 , получим уравнение , получим уравнение 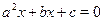 , которое подстановкой , которое подстановкой 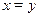 легко приводится к квадратному: легко приводится к квадратному: 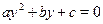 . Если . Если 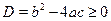 , то уравнение имеет действительные корни , то уравнение имеет действительные корни 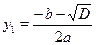 , , 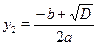 . Исходное уравнение будет иметь две группы решений: . Исходное уравнение будет иметь две группы решений: 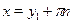 , , 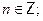 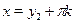 , , 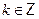 . .
Если 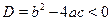 , то уравнение не имеет решений. , то уравнение не имеет решений.
Пример
Решите уравнение 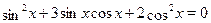 . .
Решение.
Это уравнение однородное второй степени. Разделим обе чести уравнения на 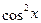 , получим: , получим: 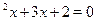 . Пусть . Пусть 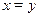 , тогда , тогда 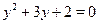 , , 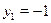 , , 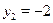 . . 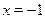 , , 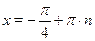 , , 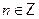 ; ; 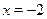 , , 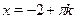 , , 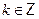 . .
Ответ.
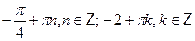 . .
К уравнению вида сводится уравнение
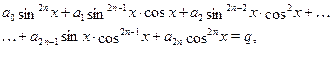
Для этого достаточно воспользоваться тождеством 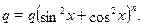
В частности, уравнение 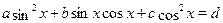 сводится к однородному, если заменить сводится к однородному, если заменить 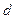 на на 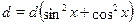 , тогда получим равносильное уравнение: , тогда получим равносильное уравнение: 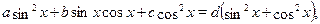
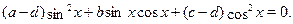
Пример
Решите уравнение 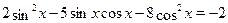 . .
Решение.
Преобразуем уравнение к однородному:
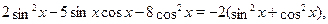
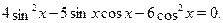
Разделим обе части уравнения на 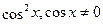 , получим уравнение: , получим уравнение:
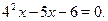 Пусть Пусть 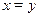 , тогда приходим к квадратному уравнению: , тогда приходим к квадратному уравнению: 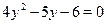 , , 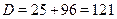 , , 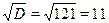 , , 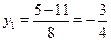 , , 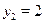 . .
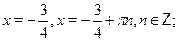
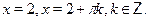
Ответ.
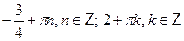 . .
Пример
Решите уравнение 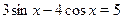 . .
Решение.
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения: 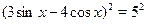 , , 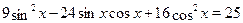 , ,
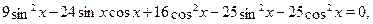
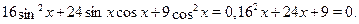
Пусть 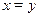 , тогда получим , тогда получим 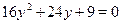 , , 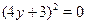 , , 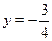 . .
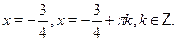
Ответ.
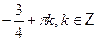 . .
Уравнения, решаемые с помощью тождеств 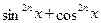
Полезно знать следующие формулы:
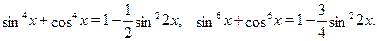
Пример
Решить уравнение 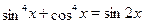 . .
Решение.
Используя , получаем
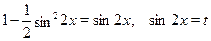
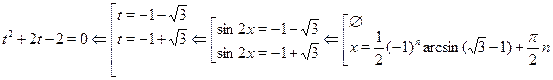
Ответ.
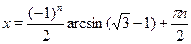
Предлагаем не сами формулы, а способ их вывода:
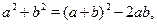
следовательно,
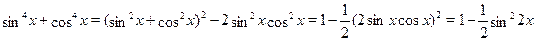 . .
Аналогично, 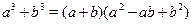 . .
Пример
Решить уравнение 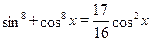 . .
Решение.
Преобразуем выражение 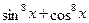 : :
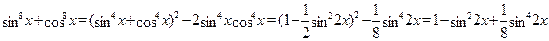 . .
Уравнение запишется в виде:
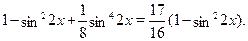
Принимая 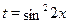 , получаем , получаем 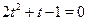 . . 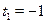 , , 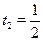 . Следовательно . Следовательно
Ответ.
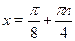 . .
Универсальная тригонометрическая подстановка
Тригонометрическое уравнение вида

где 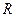 --- рациональная функция с помощью фомул -- , а так же с помощью формул -- можно свести к рациональному уравнению относительно аргументов --- рациональная функция с помощью фомул -- , а так же с помощью формул -- можно свести к рациональному уравнению относительно аргументов 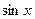 , , 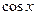 , , 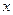 , , 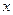 , после чего уравнение может быть сведено к алгебраическому рациональному уравнению относительно , после чего уравнение может быть сведено к алгебраическому рациональному уравнению относительно 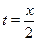 с помощью формул универсальной тригонометрической подстановки с помощью формул универсальной тригонометрической подстановки
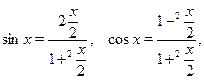
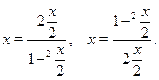
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку 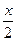 не определен в точках не определен в точках 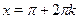 , поэтому в таких случаях нужно проверять, являются ли углы , поэтому в таких случаях нужно проверять, являются ли углы 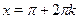 , корнями исходного уравнения. , корнями исходного уравнения.
Пример
Решить уравнение 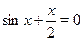 . .
Решение.
По условию задачи 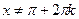 . Применив формулы и сделав замену . Применив формулы и сделав замену 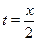 , получим , получим
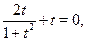
откуда 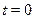 и, следовательно, и, следовательно, 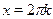 . .
Уравнения вида 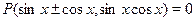
Уравнения вида 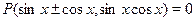 , где , где 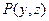 --- многочлен, решаются с помощью замен неизвестных --- многочлен, решаются с помощью замен неизвестных
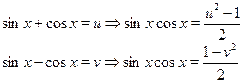
Пример
Решить уравнение 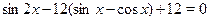 . .
Решение.
Сделав замену и учитывая, что 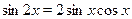 , получим , получим
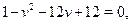
откуда 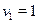 , , 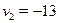 . . 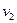 --- посторонний корень, т.к. --- посторонний корень, т.к.  . Корнями уравнения . Корнями уравнения 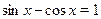 являются являются 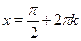 . .
НЕСТАНДАРТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
В практике централизованного тестирования не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций 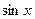 и и 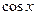 . Например: . Например:
Пример
Решить уравнение 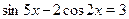 . .
Решение.
Поскольку 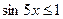 , , 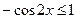 , то левая часть не превосходит , то левая часть не превосходит 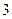 и равна и равна 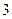 , если , если 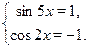
Для нахождения значений 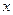 , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому. , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
Начнем со второго: 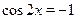 , , 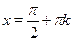 . Тогда . Тогда 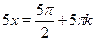 , , 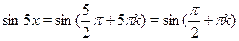 . .
Понятно, что лишь для четных 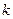 будет будет 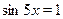 . .
Ответ.
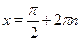 . .
Другая идея реализуется при решении следующего уравнения:
Пример
Решить уравнение 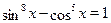 . .
Решение.
Воспользуемся свойством показательной функции: 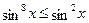 , , 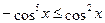 . .
Сложив почленно эти неравенства будем иметь:
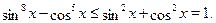
Следовательно левая часть данного уравнения равна 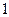 тогда и только тогда, когда выполняются два равенства: тогда и только тогда, когда выполняются два равенства:
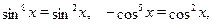
т. е. 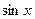 может принимать значения может принимать значения 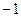 , , 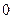 , , 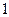 , а , а 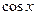 может принимать значения может принимать значения 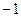 , , 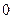 . .
Ответ.
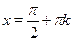 , , 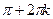 . .
Пример
Решить уравнение 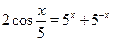 . .
Решение.
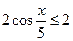 , , 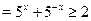 . Следовательно, . Следовательно, 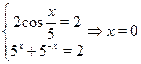 . .
Ответ.
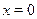 . .
Пример
Решить уравнение
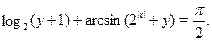
Решение.
Обозначим 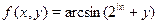 , тогда из определения обратной тригонометрической функции , тогда из определения обратной тригонометрической функции 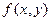 имеем имеем 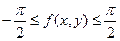 и и 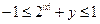 . .
Так как 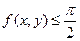 , то из уравнения следует неравенство , то из уравнения следует неравенство 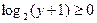 , т.е. , т.е. 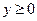 . Поскольку . Поскольку 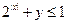 и и 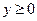 , то , то 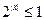 и и 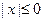 . Однако . Однако 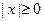 и поэтому и поэтому 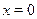 . .
Если 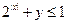 и и 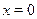 , то , то 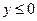 . Так как ранее было установлено, что . Так как ранее было установлено, что 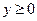 , то , то 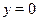 . .
Ответ.
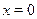 , , 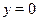 . .
Пример
Решить уравнение
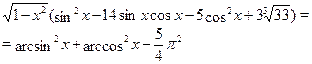
Решение.
Областью допустимых значений уравнения являются 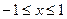 . .
Первоначально покажем, что функция
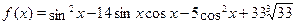 при любых при любых 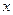 может принимать только положительные значения. может принимать только положительные значения.
Представим функцию 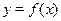 следующим образом: следующим образом: 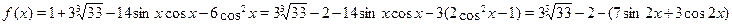 . .
Поскольку 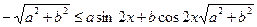 , то имеет место , то имеет место 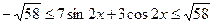 , т.е. , т.е. 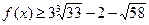 . .
Следовательно, для доказательства неравенства 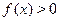 , необходимо показать, что , необходимо показать, что 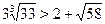 . С этой целью возведем в куб обе части данного неравенства, тогда . С этой целью возведем в куб обе части данного неравенства, тогда
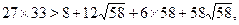
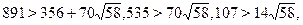
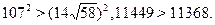
Полученное численное неравенство свидетельствует о том, что 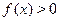 . Если при этом еще учесть, что . Если при этом еще учесть, что 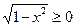 , то левая часть уравнения неотрицательна. , то левая часть уравнения неотрицательна.
Рассмотрим теперь правую часть уравнения .
Так как 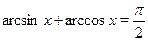 , то , то
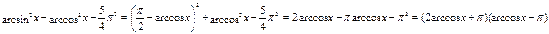 . .
Однако известно, что 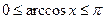 . Отсюда следует, что . Отсюда следует, что 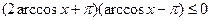 , т.е. правая часть уравнения не превосходит , т.е. правая часть уравнения не превосходит 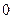 . Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны . Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны 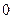 , а это возможно лишь при , а это возможно лишь при 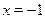 . .
Ответ.
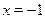 . .
Пример
Решить уравнение
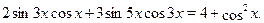
Решение.
Обозначим 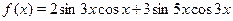 и и 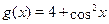 . Применяя неравенство Коши-Буняковского, получаем . Применяя неравенство Коши-Буняковского, получаем 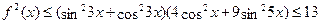 . Отсюда следует, что . Отсюда следует, что 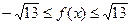 . C другой стороны имеет место . C другой стороны имеет место 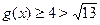 . Следовательно, уравнение не имеет корней. . Следовательно, уравнение не имеет корней.
Ответ.
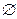 . .
Пример
Решить уравнение:
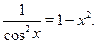
Решение.
Перепишем уравнение в виде:
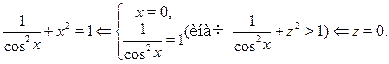
Ответ.
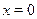 . .
Не всякое уравнение 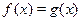 в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций 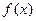 и и 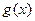 , как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке , как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке 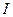 , то при наличии у уравнения , то при наличии у уравнения 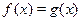 корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если же функция корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если же функция 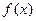 ограничена сверху, причем ограничена сверху, причем 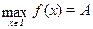 , а функция , а функция 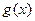 ограничена снизу, причем ограничена снизу, причем 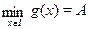 , то уравнение , то уравнение 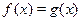 равносильно системе уравнений равносильно системе уравнений 
Пример
Решить уравнение
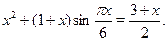
Решение.
Преобразуем исходное уравнение к виду
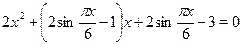
и решим его как квадратное относительно 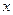 . Тогда получим, . Тогда получим,
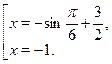
Решим первое уравнение совокупности. Учтя ограниченность функции 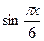 , приходим к выводу, что уравнение может иметь корень только на отрезке , приходим к выводу, что уравнение может иметь корень только на отрезке 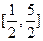 . На этом промежутке функция . На этом промежутке функция 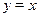 возрастает, а функция возрастает, а функция 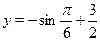 убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим 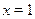 . .
Ответ.
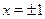 . .
Пример
Решить уравнение
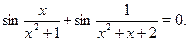
Решение.
Пусть 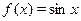 , , 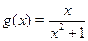 и и 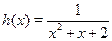 , тогда исходное уравнение можно записать в виде функционального уравнения , тогда исходное уравнение можно записать в виде функционального уравнения 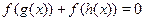 . Поскольку . Поскольку 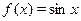 функция нечетная, то функция нечетная, то 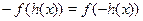 . В таком случае получаем уравнение . В таком случае получаем уравнение 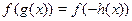 . .
Так как 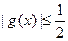 , , 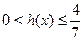 и и 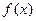 монотонна на монотонна на 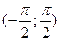 , то уравнение , то уравнение 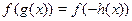 равносильно уравнению равносильно уравнению 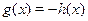 , т.е. , т.е. 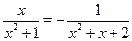 , которое имеет единственный корень , которое имеет единственный корень 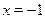 . .
Ответ.
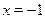 . .
Пример
Решить уравнение 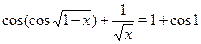 . .
Решение.
На основании теоремы о производной сложной функции ясно, что функция 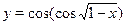 убывающая (функция убывающая (функция 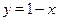 убывающая, убывающая, 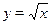 возрастающая, возрастающая, 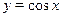 убывающая). Отсюда понятно, что функция убывающая). Отсюда понятно, что функция 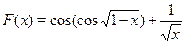 определенная на определенная на 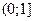 , убывающая. Поэтому данное уравнение имеет не более одного корня. Так как , убывающая. Поэтому данное уравнение имеет не более одного корня. Так как 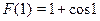 , то , то
Ответ.
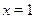 . .
Пример
Решить уравнение 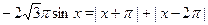 . .
Решение.
Рассмотрим уравнение на трех промежутках.
а) Пусть 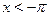 . Тогда на этом множестве исходное уравнение равносильно уравнению . Тогда на этом множестве исходное уравнение равносильно уравнению 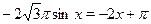 . Которое на промежутке . Которое на промежутке 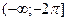 решений не имеет, т. к. решений не имеет, т. к. 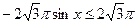 , , 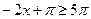 , а , а 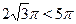 . На промежутке . На промежутке 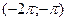 исходное уравнение так же не имеет корней, т. к. исходное уравнение так же не имеет корней, т. к. 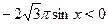 , а , а 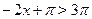 . .
б) Пусть 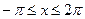 . Тогда на этом множестве исходное уравнение равносильно уравнению . Тогда на этом множестве исходное уравнение равносильно уравнению
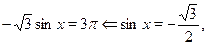
корнями которого на промежутке 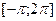 являются числа являются числа  , , 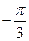 , , 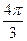 , , 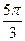 . .
в) Пусть 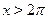 . Тогда на этом множестве исходное уравнение равносильно уравнению . Тогда на этом множестве исходное уравнение равносильно уравнению
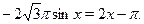
Которое на промежутке 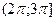 решений не имеет, т. к. решений не имеет, т. к. 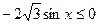 , а , а 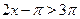 . На промежутке . На промежутке 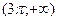 уравнение так же решений не имеет, т. к. уравнение так же решений не имеет, т. к. 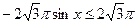 , , 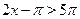 , а , а 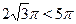 . .
Ответ.
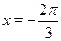 , , 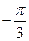 , , 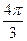 , , 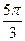 . .
Метод симметрии удобно применять, когда в формулировке задания присуствует требование единственности решения уравнения, неравенства, системы и т.п. или точное указание числа решений. При этом следует обнаружить какую-либо симметрию заданных выражений.
Нужно также учитывать многообразие различных возможных видов симметрии.
Не менее важным является четкое соблюдение логических этапов в рассуждениях с симметрией.
Обычно симметрия позволяет установить лишь необходимые условия, а затем требуется проверка их достаточности.
Пример
Найти все значения параметра  , при которых уравнение , при которых уравнение 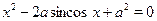 имеет единственное решение. имеет единственное решение.
Решение.
Заметим, что 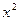 и и 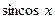 --- четные функции, поэтому левая часть уравнения есть четная функция. --- четные функции, поэтому левая часть уравнения есть четная функция.
Значит если 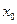 --- решение уравнения, то --- решение уравнения, то 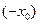 есть также решение уравнения. Если есть также решение уравнения. Если 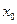 --- единственное решение уравнения, то, необходимо
, --- единственное решение уравнения, то, необходимо
, 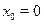 . .
Отберем возможные
значения  , потребовав, чтобы , потребовав, чтобы 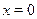 было корнем уравнения. было корнем уравнения.
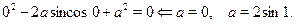
Сразу же отметим, что другие значения  не могут удовлетворять условию задачи. не могут удовлетворять условию задачи.
Но пока не известно, все ли отобранные  в действительности удовлетворяют условию задачи. в действительности удовлетворяют условию задачи.
Достаточность.
1) 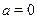 , уравнение примет вид , уравнение примет вид 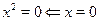 . .
2) 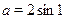 , уравнение примет вид: , уравнение примет вид:
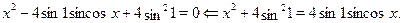
Очевидно, что 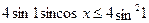 , для всех , для всех 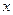 и и 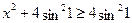 . Следовательно, последнее уравнение равносильно системе: . Следовательно, последнее уравнение равносильно системе:
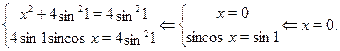
Тем самым, мы доказали, что при 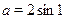 , уравнение имеет единственное решение. , уравнение имеет единственное решение.
Ответ.
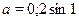 . .
Пример
Докажите, что все решения уравнения
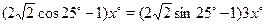
--- целые числа.
Решение.
Основной период исходного уравнения равен 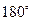 . Поэтому сначала исследуем это уравнение на отрезке . Поэтому сначала исследуем это уравнение на отрезке 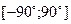 . .
Преобразуем уравнение к виду:
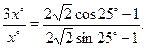
При помощи микрокалькулятора получаем:
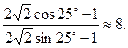
Находим:
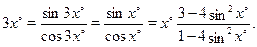
Если 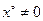 , то из предыдущих равенств получаем: , то из предыдущих равенств получаем:
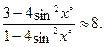
Решив полученное уравнение, получим: 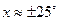 . .
Выполненные вычисления представляют возможность предположить, что корнями уравнения, принадлежащими отрезку 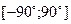 , являются , являются 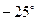 , , 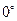 и и 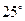 . .
Непосредственная проверка подтверждает эту гипотезу. Таким образом, доказано, что корнями уравнения являются только целые числа 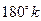 , , 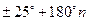 . .
Пример
Решите уравнение 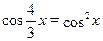 . .
Решение.
Найдём основной период уравнения. У функции 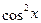 основной период равен основной период равен 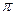 . Основной период функции . Основной период функции 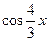 равен равен 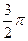 . Наименьшее общее кратное чисел . Наименьшее общее кратное чисел 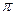 и и 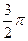 равно равно 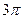 . Поэтому основной период уравнения равен . Поэтому основной период уравнения равен 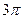 . Пусть . Пусть 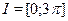 . .
Очевидно, 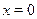 является решением уравнения. На интервале является решением уравнения. На интервале 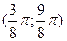 . Функция . Функция 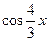 отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx 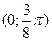 и и 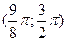 . .
При помоши микрокалькулятора сначала найдем приближенные значения корней уравнения. Для этого составляем таблицу значений функции 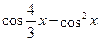 на интервалах на интервалах 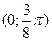 и и 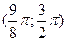 ; т. е. на интервалах ; т. е. на интервалах 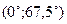 и и 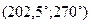 . .
 |
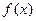 |
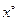 |
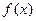 |
| 0 |
0 |
202,5 |
0,85355342 |
| 3 |
-0,00080306 |
207 |
0,6893642 |
| 6 |
-0,00119426 |
210 |
0,57635189 |
| 9 |
-0,00261932 |
213 |
0,4614465 |
| 12 |
-0,00448897 |
216 |
0,34549155 |
| 15 |
-0,00667995 |
219 |
0,22934931 |
| 18 |
-0,00903692 |
222 |
0,1138931 |
| 21 |
-0,01137519 |
225 |
0,00000002 |
| 24 |
-0,01312438 |
228 |
-0,11145712 |
| 27 |
-0,01512438 |
231 |
-0,21961736 |
| 30 |
-0,01604446 |
234 |
-0,32363903 |
| 33 |
-0,01597149 |
237 |
-0,42270819 |
| 36 |
-0,01462203 |
240 |
-0,5160445 |
| 39 |
-0,01170562 |
243 |
-0,60290965 |
| 42 |
-0,00692866 |
246 |
-0,65261345 |
| 45 |
0,00000002 |
249 |
-0,75452006 |
| 48 |
0,00936458 |
252 |
-0,81805397 |
| 51 |
0,02143757 |
255 |
-0,87270535 |
| 54 |
0,03647455 |
258 |
-0,91803444 |
| 57 |
0,0547098 |
261 |
-0,95367586 |
| 60 |
0,07635185 |
264 |
-0,97934187 |
| 63 |
0,10157893 |
267 |
-0,99482505 |
| 66 |
0,1305352 |
270 |
-1 |
| 67,5 |
0,14644661 |
Из таблицы легко усматриваются следующие гипотезы: корнями уравнения, принадлежащими отрезку 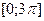 , являются числа: , являются числа: 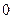 ; ; 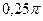 ; ; 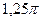 . Непосредственная проверка подтверждает эту гипотезу. . Непосредственная проверка подтверждает эту гипотезу.
Ответ.
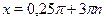 ; ; 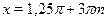 ; ; 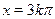 . .
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
При решении тригонометрических неравенств вида 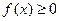 , где , где 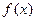 --- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа --- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа 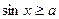 . Разберём на примере, как решать такие неравенства. . Разберём на примере, как решать такие неравенства.
Пример
Решите неравенство 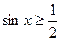 . .
Решение.
Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит 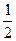 . .

Для 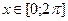 решением данного неравенства будут решением данного неравенства будут 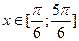 . Ясно также, что если некоторое число . Ясно также, что если некоторое число 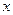 будет отличаться от какого-нибудь числа из указанного интервала на будет отличаться от какого-нибудь числа из указанного интервала на 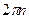 , то , то 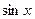 также будет не меньше также будет не меньше 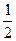 . Следовательно, к концам найденного отрезка решения нужно просто добавить . Следовательно, к концам найденного отрезка решения нужно просто добавить 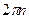 . Окончательно, получаем, что решениями исходного неравенства будут все . Окончательно, получаем, что решениями исходного неравенства будут все 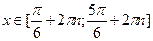 . .
Ответ.
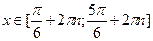 . .
Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые 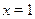 и и 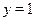 соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности. соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности.
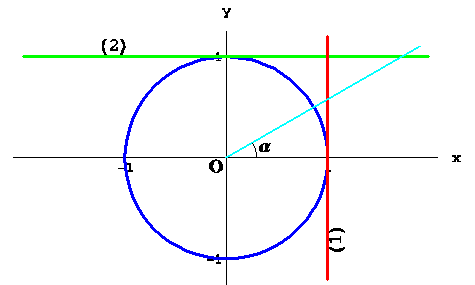
Легко заметить, что если построить луч с началом в начале координат, составляющий угол 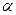 с положительным направлением оси абсцисс, то длина отрезка от точки с положительным направлением оси абсцисс, то длина отрезка от точки 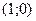 до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса. до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
Пример
Решите неравенство 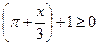 . .
Решение.
Обозначим 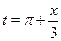 , тогда неравенство примет вид простейшего: , тогда неравенство примет вид простейшего: 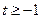 . Рассмотрим интервал . Рассмотрим интервал 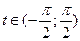 длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что 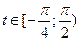 . Вспоминаем теперь, что необходимо добавить . Вспоминаем теперь, что необходимо добавить 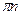 , поскольку НПП функции , поскольку НПП функции 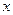  . Итак, . Итак, 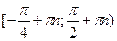 . Возвращаясь к переменной . Возвращаясь к переменной 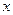 , получаем, что , получаем, что 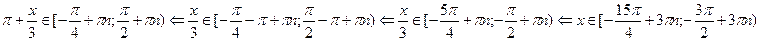 . .
Ответ.
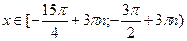 . .
Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере.
Заметим, что если 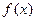 --- периодическая функция, то для решения неравенства --- периодическая функция, то для решения неравенства 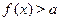 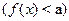 необходимо найти его решения на отрезке, длина которого равна периоду функции необходимо найти его решения на отрезке, длина которого равна периоду функции 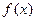 . Все решения исходного неравенства будут состоять из найденных значений . Все решения исходного неравенства будут состоять из найденных значений 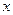 , а также всех , а также всех 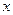 , отличающихся от найденных на любое целое число периодов функции , отличающихся от найденных на любое целое число периодов функции 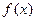 . .
Рассмотрим решение неравенства 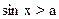 ( (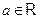 ). ).
Поскольку 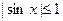 , то при , то при 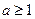 неравенство решений не имеет. Если неравенство решений не имеет. Если 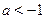 , то множество решений неравенства , то множество решений неравенства 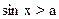 --- множество всех действительных чисел. --- множество всех действительных чисел.
Пусть 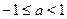 . Функция синус имеет наименьший положительный период . Функция синус имеет наименьший положительный период 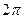 , поэтому неравенство , поэтому неравенство 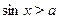 можно решить сначала на отрезке длиной можно решить сначала на отрезке длиной 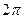 , например, на отрезке , например, на отрезке 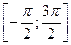 . Строим графики функций . Строим графики функций 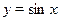 и и 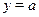 ( ( ). ).
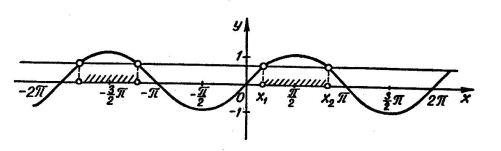
На отрезке 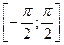 функция синус возрастает, и уравнение функция синус возрастает, и уравнение 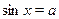 , где , где  , имеет один корень , имеет один корень 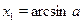 . На отрезке . На отрезке 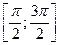 функция синус убывает, и уравнение функция синус убывает, и уравнение 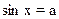 имеет корень имеет корень 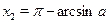 . На числовом промежутке . На числовом промежутке 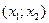 график функции график функции 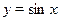 расположен выше графика функции расположен выше графика функции 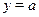 . Поэтому для всех . Поэтому для всех 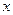 из промежутка из промежутка 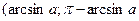 ) неравенство ) неравенство 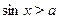 выполняется, если выполняется, если 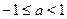 . В силу периодичности функции синус все решения неравенства . В силу периодичности функции синус все решения неравенства 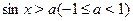 задаются неравенствами вида: задаются неравенствами вида: 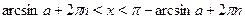 . .
Аналогично решаются неравенства 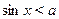 , , 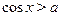 , и т.п. , и т.п.
Пример
Решим неравенство 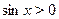 . .
Решение.
Рассмотрим график функции 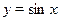
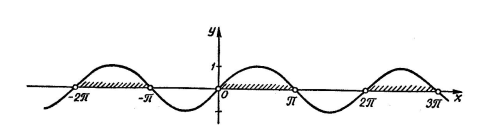
и выберем из промежутка 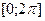 на оси на оси 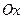 значения аргумента значения аргумента 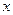 , которым соответствуют точки графика, лежащие выше оси , которым соответствуют точки графика, лежащие выше оси 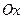 . Таким промежутком является интервал . Таким промежутком является интервал 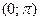 . Учитывая периодичность функции . Учитывая периодичность функции 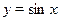 все решения неравенства все решения неравенства 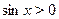 можно записать так: можно записать так: 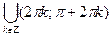 . .
Ответ.
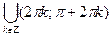 . .
Пример
Решите неравенство 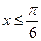 . .
Решение.
Нарисуем график функции 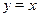 . Найдём точку пересечения этого графика с горизонтальной прямой . Найдём точку пересечения этого графика с горизонтальной прямой 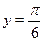 . .
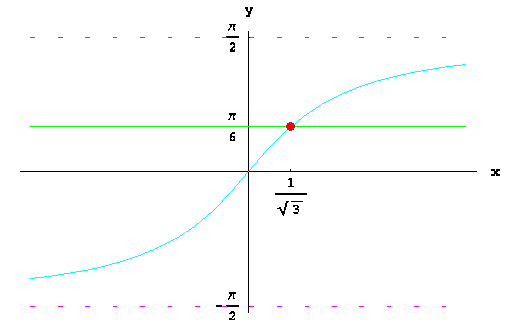
Это точка с абсциссой 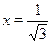 . По графику видно, что для всех . По графику видно, что для всех 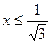 график функции лежит ниже прямой график функции лежит ниже прямой 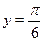 . Следовательно, эти . Следовательно, эти 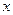 и составляют: и составляют:
Ответ.
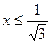 . .
ОТБОР КОРНЕЙ
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведем решения уравнений, иллюстрирующие типичные случаи появления посторонних корней и методы <<борьбы>> с ними.
Пример
Найти ближайший к числу 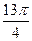 корень уравнения корень уравнения
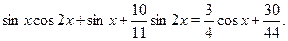
Решение.
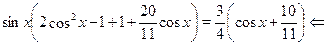
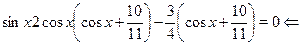
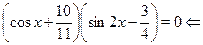
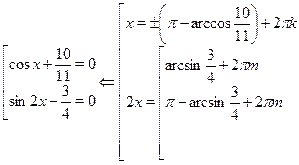
Подставляя последовательно в формулу 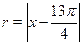 вместо переменной вместо переменной 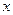 выписанные выше серии решений уравнений, отыщем для каждой из них выписанные выше серии решений уравнений, отыщем для каждой из них 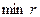 , а затем сравним полученные минимальные , а затем сравним полученные минимальные 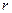 между собой. между собой.
a) 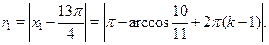
Ясно, что 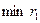 достигается при достигается при 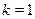 , то есть , то есть 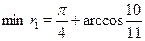 . .
б)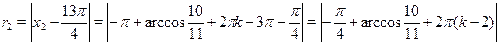
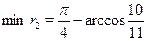 . .
в)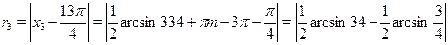 . .
г)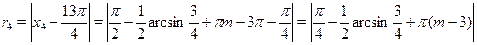 . .
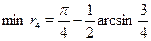 . .
Выберем минимальное из чисел 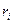 , , 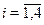 . Сразу ясно, что . Сразу ясно, что 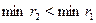 и что и что 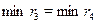 . Оталось сравнить . Оталось сравнить 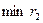 и и 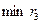 . Предположим, что . Предположим, что
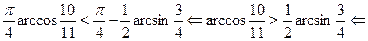
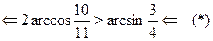
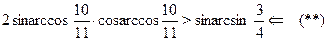
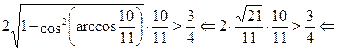
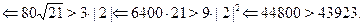
Последнее неравенство --- верное, а все сделанные переходы --- равносильные. Поэтому верно исходное неравенство. Обоснуем равносильность переходов (*) и (**) (равносильность остальных переходов следует из общих свойств числовых неравнств). В случае преобраования (*), достаточно заметить, что числа 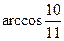 и и 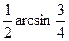 расположен на участке расположен на участке  монотонного возрастания функции монотонного возрастания функции 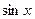 . В случае перехода (**) формула . В случае перехода (**) формула 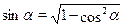 справедлива, так как справедлива, так как 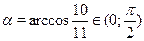 . .
Ответ.
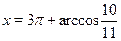 . .
Пример
Найти корни уравнения: 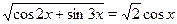 . .
Решение этого уравнения распадается на два этапа: 1) решение уравнения, получающегося из данного возведением в квадрат обеих его частей; 2) отбор тех корней, которые удовлетворяют условию 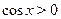 . При этом заботится об условии . При этом заботится об условии 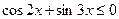 нет необходимости. Все значения нет необходимости. Все значения 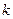 , удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют. , удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют.
Первый шаг нас приводит к уравнению 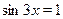 , откуда , откуда 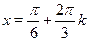 . .
Теперь надо определить, при каких 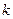 будет будет 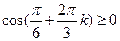 . Для этого достаточно для . Для этого достаточно для 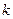 рассмотреть значения рассмотреть значения 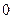 , , 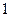 , , 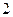 , т. е. <<обойти один раз круг>>, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную , т. е. <<обойти один раз круг>>, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную 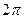 . .
Ответ.
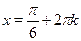 , , 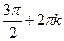 . .
Итак, основная схема отбора корней состоит в следующем. Находится наименьший общий период всех тригонометрических функций входящих в уравнение. На этом периоде отбираются корни, а затем оставшиеся корни периодически продолжаются.
Пример
Решить уравнение:

Решение.
Уравнение равносильно смешанной системе:
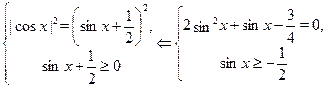
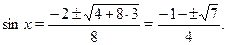
Но 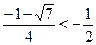 --- не годится. --- не годится.
Ответ.
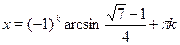 . .
Раскрывая знак модуля получаем более громоздное решение. А ответ в этом случае принимает вид:
Ответ.
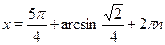 . .
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Тест по теме <<Тригонометрические уравнения>>
• Объединение каких множеств 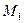 , , 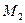 , , 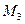 , , 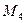 является решением уравнения является решением уравнения 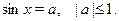
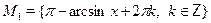 , ,  , , 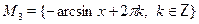 , , 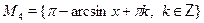 . .
a) 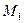 , , 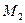 б) б) 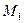 , , 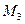 в) в) 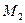 , , 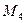 г) г) 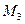 , , 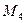
• Решите уравнение 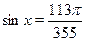 . .
a)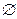 б) б)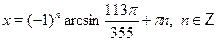 в) в) 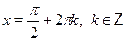 г) г) 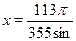
• Решите уравнение 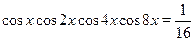 . .
a) 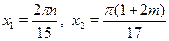
б) 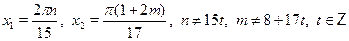
в) 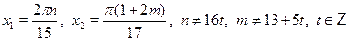
г) 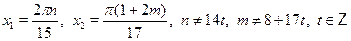
• Решите уравнение 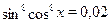 . .
a) 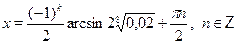
б) 
в) 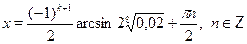
г) 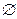
• Решите уравнение 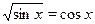 . .
a) 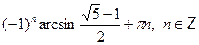
б) 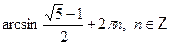
в) 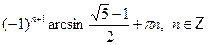
г) 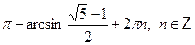
• Среди множеств 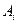 , , 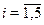 найдите решение уравнения найдите решение уравнения
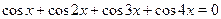
и укажите те, которые не являются подмножествами друг друга.
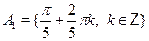 , , 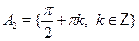 , , 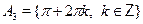 , , 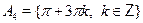 , , 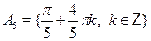 . .
а) 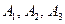 б) б) 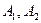 в) в) 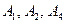 г) г) 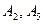
• Среди множеств 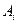 , , 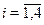 найдите решение уравнения найдите решение уравнения
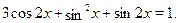
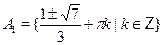
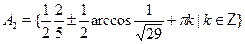
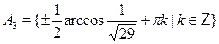
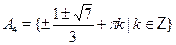
а) 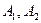 б) б) 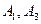 в) в) 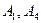 г) г)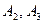
• Решите уравнение 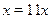 . .
а) 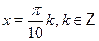 б) б) 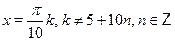
в) 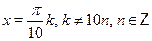 г) г) 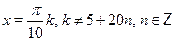
• Решите уравнение
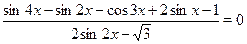
а) 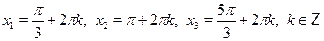
б) 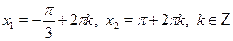
в) 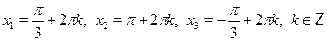
г) 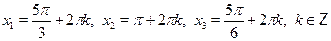
• Решите уравнение 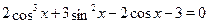 . .
а) 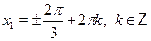 б) б) 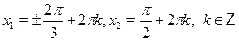
в) 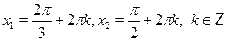 г) г) 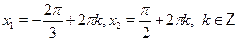
• Сумма корней уравнения 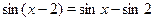 на отрезке на отрезке 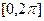 равна: равна:
а) 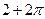 б) б) 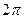 в) в) 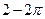 г) г) 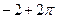
• Решите уравнение
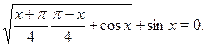
В ответе записать количество корней уравнения, принадлежащих отрезку 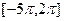 . .
а) 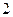 б) б) 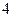 в) в) 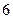 г) г) 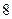
• Решить уравнение 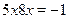
а) 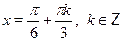 б) б) 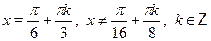
в) 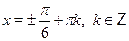 г) г) 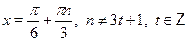
• Решите уравнение 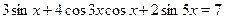 . .
a) 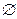 б) б) 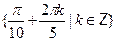
в) 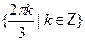 г) г) 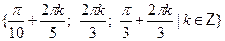
• Решите уравнение
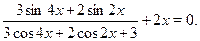
a) 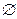
б) 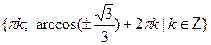
в) 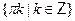
г) 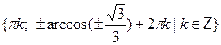
Найдите набольший отрицательный корень уравнения:
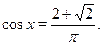
a) 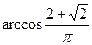 б) б) 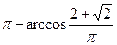
в) 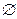 г) г) 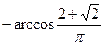
• Решите уравнение 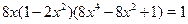 на множестве на множестве 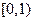 . .
a) 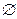
б) 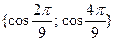
в) 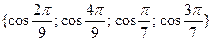
г) 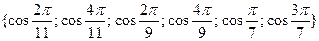
• Решите уравнение 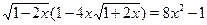 . .
a) 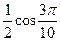 б) б) 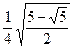
в) 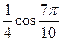 г) г) 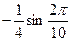
• Решить уравнение 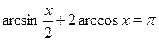 . .
а) 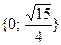 б) б) 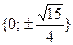 в) в) 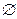 г) г) 
• Решите уравнение 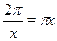 . .
a) 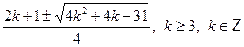
б) 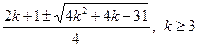 или или 
в) 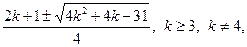 или или  и и 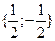
г) 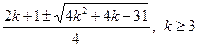 или или  и и 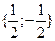
Ответы
1а 2б 3б 4г 5б 6б 7а 8б 9г 10б 11а 12б 13в или г 14а 15в 16в 17в 18а или б 19г 20в
ЗАКЛЮЧЕНИЕ
В данной работе были рассмотрены методы решения тригонометрических уравнений и неравенств, как простейших, так и олимпиадного уровня. Были рассмотрены основные методы решения тригонометрических уравнений и неравенств, причем, как специфические --- характерные только для тригонометрических уравнений и неравенств,--- так и общие функциональные методы решения уравнений и неравенств, применительно к тригонометрическим уравнениям.
В дипломной работе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов. Приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
Результаты данной дипломной работы могут быть использованы в качестве учебного материала при подготовке курсовых и дипломных работ, при составлении факультативов для школьников, так же работа может применяться при подготовке учащихся к вступительным экзаменам и централизованному тестированию.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Выгодский Я.Я., Справочник по элементарной математике. /Выгодский Я.Я. --- М.: Наука, 1970.
Игудисман О., Математика на устном экзамене/ Игудисман О. --- М.: Айрис пресс, Рольф, 2001.
Азаров А.И., уравнения/Азаров А.И., Гладун О.М., Федосенко В.С. --- Мн.: Тривиум, 1994.
Литвиненко В.Н., Практикум по элементарной математике / Литвиненко В.Н.--- М.: Просвещение, 1991.
Шарыгин И.Ф., Факультативный курс по математике: решение задач/ Шарыгин И.Ф., Голубев В.И. --- М.: Просвещение, 1991.
Бардушкин В., Тригонометрические уравнения. Отбор корней/В. Бардушкин, А. Прокофьев.// Математика, №12, 2005 с. 23--27.
Василевский А.Б., Задания для внеклассной работы по математике/Василевский А.Б. --- Мн.: Народная асвета. 1988. --- 176с.
Сапунов П. И., Преобразование и объединение групп общих решений тригонометрических уравнений/Сапунов П. И. // Математическое просвещение, выпуск №3, 1935.
Бородин П., Тригонометрия. Материалы вступительных экзаменов в МГУ[текст]/П.Бородин, В.Галкин, В.Панфёров, И.Сергеев, В.Тарасов // Математика №1, 2005 с. 36--48.
Самусенко А.В., Математика: Типичные ошибки абитуриентов: Справочное пособие/Самусенко А.В., Казаченок В.В.--- Мн.: Вышейшая школа, 1991.
Азаров А.И., Функциональный и графический методы решения экзаменационных задач/Азаров А.И., Барвенов С.А.,--- Мн.: Аверсэв, 2004.
|