| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
(филиал в г. Воскресенске)
Кафедра «Прикладной математики»
КУРСОВАЯ РАБОТА
Дисциплина: «Моделирование микроэкономических процессов и систем»
Тема: « Использование математических методов и моделей в управлении микроэкономическими системами »
Выполнил:
студент 4-го курса (очное отделение)
Петров А.Ю. (шифр1906361)
Специальность: 080116 –
«Математические методы в экономике»
Руководитель:
ст. преподаватель Нидеккер И.А.
Воскресенск, 2009 г.
Оглавление
Введение
Раздел I. «Сетевые модели»
Раздел II. «Использование метода анализа иерархий для организации поставок»
Заключение
Литература
Введение
Темой данной курсовой работы является «Использование математических методов и моделей в управлении микроэкономическими системами».
Курсовая работа имеет следующую структуру:
1. Введение
2. Раздел I «Сетевые модели».
3. Раздел II «Использование метода анализа иерархий для организации поставок».
4. Заключение
5. Список использованной литературы
Целью курсовой работы является изучение на практике современных методов управления и организации производства, совершенствование применения этих методов.
В первом разделе курсовой работы рассматривается ориентированная сеть, рассчитываются необходимые показатели этой сети для принятия в дальнейшем управленческих решений. На примерах описываются возможные применения данных методов.
Во втором разделе рассматривается проблема выбора поставщика. Оценивается по критериям каждый из них, и в результате расчетов принимается решение о продолжении сотрудничества с одним из поставщиков.
Раздел
I.
«Сетевые модели»
1. Построение сети.
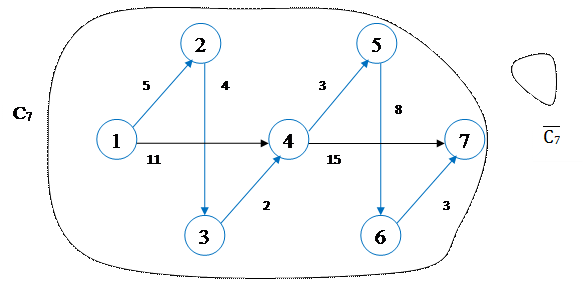
Данная ориентированная сеть состоит из 7 вершин, соединенных 8 ребрами. Источник – вершина 1, сток – вершина 7. Веса ребер указаны на сети, а также в таблице 1.
Таблица 1
| Ребро (i, j)
|
Вес ребра (i, j)
|
| (1, 2)
|
5
|
| (1, 4)
|
11
|
| (2, 3)
|
4
|
| (3, 4)
|
2
|
| (4, 5)
|
3
|
| (4, 7)
|
15
|
| (5, 6)
|
8
|
| (6, 7)
|
3
|
2. Построение минимального остовного дерева.
Минимальное остовное дерево - это остовное дерево графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
Реклама

Шаг 0
: C0
= Ø, 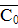 = {1, 2, 3, 4, 5, 6, 7} = {1, 2, 3, 4, 5, 6, 7}
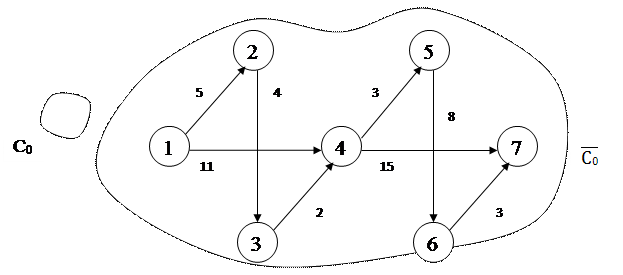
 Шаг 1
: C1
= {1}, Шаг 1
: C1
= {1},  = {2, 3, 4, 5, 6, 7} = {2, 3, 4, 5, 6, 7}
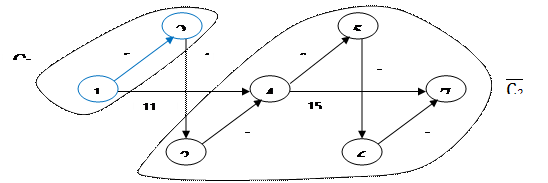 Шаг 2
: min l (1-2) = 5, j* = {2}, C2
= {1, 2}, Шаг 2
: min l (1-2) = 5, j* = {2}, C2
= {1, 2}, 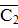 = {3, 4, 5, 6, 7} = {3, 4, 5, 6, 7}
 Шаг 3
: min l (2-3) = 4, j* = {3}, C3
= {1, 2, 3}, Шаг 3
: min l (2-3) = 4, j* = {3}, C3
= {1, 2, 3},  = {4, 5, 6, 7} = {4, 5, 6, 7}
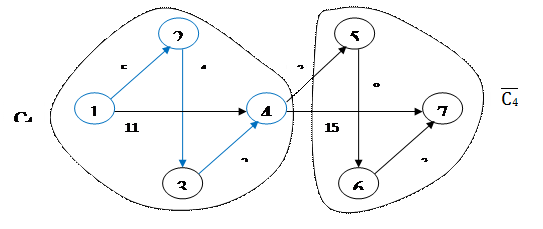 Шаг 4
: min l (3-4) = 2, j* = {4}, C4
= {1, 2, 3, 4}, Шаг 4
: min l (3-4) = 2, j* = {4}, C4
= {1, 2, 3, 4}, 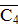 = {5, 6, 7} = {5, 6, 7}
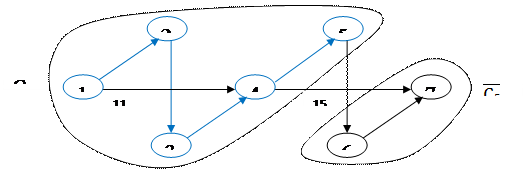 Шаг 5
: min l (4-5) = 3, j* = {5}, C5
= {1, 2, 3, 4, 5}, Шаг 5
: min l (4-5) = 3, j* = {5}, C5
= {1, 2, 3, 4, 5},  = {6, 7} = {6, 7}
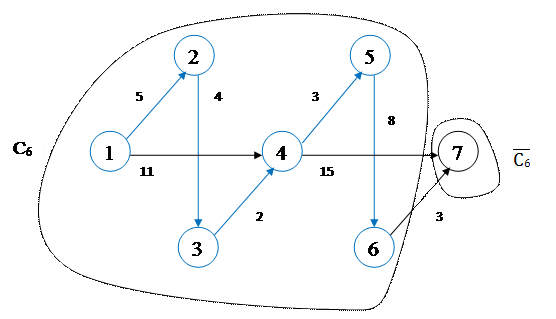 Шаг 6
: min l (5-6) = 8, j* = {6}, C6
= {1, 2, 3, 4, 5, 6}, Шаг 6
: min l (5-6) = 8, j* = {6}, C6
= {1, 2, 3, 4, 5, 6},  = {7} = {7}
 Шаг 7
: min l (6-7) = 3, j* = {7}, C7
= {1, 2, 3, 4, 5, 6, 7}, Шаг 7
: min l (6-7) = 3, j* = {7}, C7
= {1, 2, 3, 4, 5, 6, 7},  = Ø = Ø
Минимальное остовное дерево будет выглядеть следующим образом:
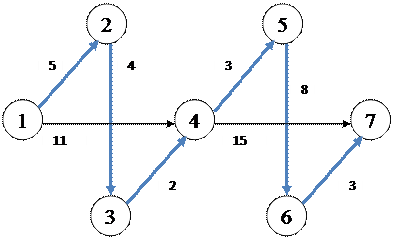
Сумма весов ребер остовного дерева равна 5+4+2+3+8+3 = 25 ед.
Пример:
Необходимо соединить населенные пункты под номерами 1 – 7 автомобильными дорогами, при условии, что их протяженность будет минимальна.
Расстояния указаны рядом с каждым ребром сети.
Построение минимального остовного дерева решает эту задачу.
При этом протяженность автомобильных дорог, соединяющих все населенные пункты, будет равна 25 километрам.
3. Нахождение кратчайшего маршрута.
Нахождение кратчайшего маршрута заключается в соединении источника (1) со стоком (7) минимальным расстоянием.
Шаг 1: Начальная точка {1}.
Находим кратчайший маршрут до следующей точки.
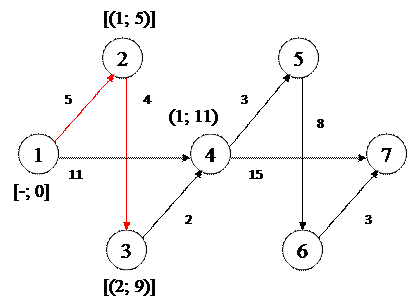 Шаг 2: Точки {1} и {2} соединяем кратчайшим маршрутом со следующей точкой. Шаг 2: Точки {1} и {2} соединяем кратчайшим маршрутом со следующей точкой.
Шаг 3: Точки {1} и {3} соединяем кратчайшим маршрутом со следующей точкой.
В результате получаем два альтернативных пути – один из них обозначен пунктиром.
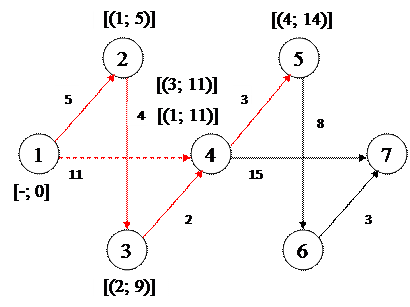 Шаг 4: Точку {4} соединяем кратчайшим маршрутом со следующей точкой. Шаг 4: Точку {4} соединяем кратчайшим маршрутом со следующей точкой.
Шаг 5: Точки {4} и {5} соединяем кратчайшим маршрутом со следующей точкой.
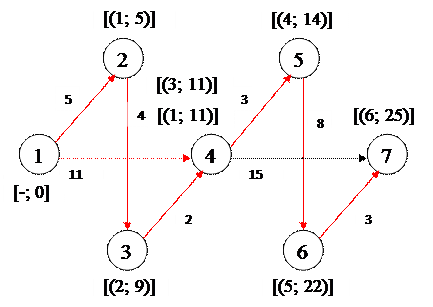 Шаг 6: Точки {4} и {6} соединяем кратчайшим маршрутом со следующей точкой. Шаг 6: Точки {4} и {6} соединяем кратчайшим маршрутом со следующей точкой.
В результате итераций мы нашли кратчайшие маршруты, записанные ниже в таблицу 2.
Таблица 2
| Узел сети
|
Кратчайший маршрут
|
| топология
|
протяженность
|
| 2
|
1-2
|
5
|
| 3
|
1-2-3
|
9
|
| 4
|
1-2-3-4 или 1-4
|
11
|
| 5
|
1-2-3-4-5 или 1-4-5
|
14
|
| 6
|
1-2-3-4-5-6 или 1-4-5-6
|
22
|
| 7
|
1-2-3-4-5-6-7 или 1-4-5-6-7
|
25
|
Пример:
Транспортная компания выбирает маршрут из пункта 1 в пункт 7 для доставки товара и желает сократить время в пути своего автотранспорта. Время необходимое для перевозки товара по каждому участку пути обозначено рядом с каждым ребром сети. Необходимо проложить маршрут, обеспечивающий минимальное время автотранспорта в пути.
С помощью алгоритма построения кратчайшего маршрута такой тип задачи можно решить. В результате расчетов минимальное время в пути будет составлять 25 часов.
Реклама

4. Нахождение максимального потока.
Найти максимальный поток можно одним из нижеописанных способов.
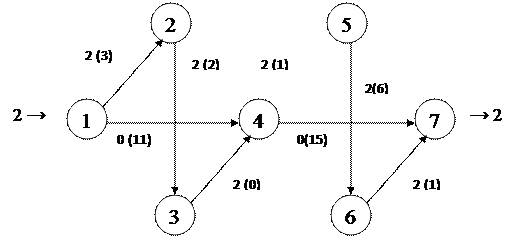
4.1 Серия последовательных шагов.
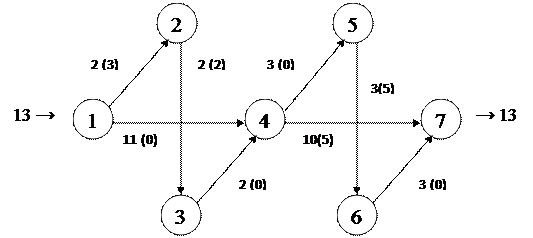
На графиках укажем степень насыщения потока над каждым ребром, а в скобках остаточную пропускную способность.
Шаг 1: построим поток 1-2-3-4-5-6-7 и найдем максимальную пропускную способность этого пути.
 Min
(
Cij
) =
C
34
= 2 Min
(
Cij
) =
C
34
= 2
 Φ
1
= 2 Φ
1
= 2
Поток не полный
Шаг 2: построим поток 1-4-5-6-7
Min
(
Cij
) =
C
45
= 1
Φ
2
=
Φ
1
+ 1= 3
Поток не полный
Шаг 3: построим поток 1-4-7
Min
(
Cij
) =
C
14
= 10
 Φ
3
=
Φ
2
+ 10= 13 Φ
3
=
Φ
2
+ 10= 13
Φ
3
=13 – полный поток
4.2 Метод разделяющих сечений
Обозначим все возможные разделяющие сечения данной сети и опишем их характеристики ниже.
1)  Χ = {1}, Χ = {1}, 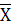 = {2, 3, 4, 5, 6, 7} = {2, 3, 4, 5, 6, 7}
С1
= С(1; 2) + С(1; 3) = 5+11=16
2)  Χ = {1, 2}, Χ = {1, 2}, 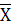 = {3, 4, 5, 6, 7} = {3, 4, 5, 6, 7}
С2
= С(1; 4) + С(2; 3) = 11+4=15
3) 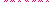 Χ = {1, 3}, Χ = {1, 3}, 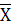 = {2, 4, 5, 6, 7} = {2, 4, 5, 6, 7}
С3
= С(1; 2) + С(2; 3) + С(1, 4) + С(3, 4) = 5+4+11+2=22
4)  Χ = {1, 2, 3}, Χ = {1, 2, 3}, 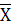 = {4, 5, 6, 7} = {4, 5, 6, 7}
С4
= С(1; 4) + С(3, 2) = 11+2=13
5)  Χ = {1, 2, 3, 4}, Χ = {1, 2, 3, 4}, 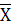 = {5, 6, 7} = {5, 6, 7}
С5
= С(4; 5) + С(4, 7) = 3+15=18
6)  Χ = {1, 2, 3, 4, 5}, Χ = {1, 2, 3, 4, 5}, 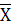 = {6, 7} = {6, 7}
С6
= С(4; 7) + С(5, 6) = 8+15=23
7)  Χ = {1, 2, 3, 4, 6}, Χ = {1, 2, 3, 4, 6},  = {5, 7} = {5, 7}
С7
= С(4; 5) + С(4, 7) + С(5, 6) + С(6, 7) = 3+15+8+3=29
8)  Χ = {1, 2, 3, 4, 5, 6}, Χ = {1, 2, 3, 4, 5, 6},  = {7} = {7}
С8
= С(4; 7) + С(6, 7) = 15+3=18
Минимальное сечение:
Max Φ = min Ci
= min(16, 15, 22, 13, 18, 23, 29, 18) = 13
4.3 Ребра, обеспечивающие пропуск максимального потока через заданную сеть – выделены зеленым цветом. В скобках указана неиспользованная пропускная способность ребра.
4.4
Пример:
Компания, занимающаяся прокладкой газопровода, решает задачу о замене некоторых участков, в связи с увеличившимся спросом у потребителей. Для этого необходимо выявить «узкие» участки газопровода. Пропускные способности каждого участка указаны рядом с ребрами.
После построения полного и максимального потока видно, что участки 1 – 4, 3 – 4, 4 – 5, 6 – 7 нагружены полностью, в то время как на участках 1 – 2, 2 – 3, 4 – 7, 5 – 6 не использована пропускная способность в размерах 3, 2, 5, 5 соответственно.
Раздел II. «Использование метода анализа иерархий для организации поставок»
Предприятие решает вопрос о продлении договора на поставку с одним из поставщиков, основываясь на результатах работы по уже заключенным договорам. Поставщики оцениваются по критериям:
К1 – надежность поставки
К2 – цена
К3 – качество товара
К4 – условия платежа
К5 – возможность внеплановых поставок
Матрица сравнений критериев относительно цели:
Матрицы сравнения альтернатив (поставщиков) относительно критериев:
  k1 k2 k3 k4 k5 k1 k2 k3 k4 k5
  
Найдем веса критериев и проверим согласованность матрицы сравнения критериев. При несогласованности матрицы найдем противоречия в суждениях ЛПР, изменим результаты сравнения и проверим согласованность матрицы заново.
Для матрицы сравнения критериев относительно цели найдем собственный вектор и вес каждого критерия:
| Критерий
|
k1
|
k2
|
k3
|
k4
|
k5
|
собственный вектор
|
вес
|
| k1
|
1
|
5
|
8
|
2
|
7
|
3,545
|
0,535
|
| k2
|
1/5
|
1
|
3
|
4
|
1/2
|
1,037
|
0,157
|
| k3
|
1/8
|
1/3
|
1
|
2
|
1
|
0,608
|
0,092
|
| k4
|
1/2
|
1/4
|
1/2
|
1
|
1/3
|
0,461
|
0,070
|
| k5
|
1/7
|
2
|
1
|
3
|
1
|
0,970
|
0,146
|
| Σ
|
6,621
|
1,000
|
Проверим согласованность матрицы:
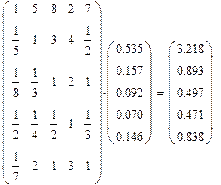
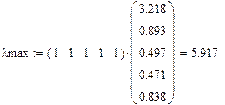
n = 5
L = 0,229
R = 1,120
T = 0,204 > 0,1 – уровень согласованности не приемлем.
Изменим суждения ЛПР для достижения согласованности матрицы.
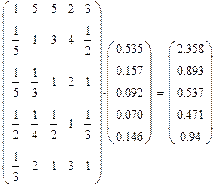
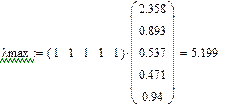
n = 5
L = 0,049
R = 1,120
T = 0,043 < 0,1 – уровень согласованности приемлем.
1. Найдем веса альтернатив по критериям и проверим их согласованность.
Альтернативы относительно критерия
k1
| Альтернативы
|
A1
|
A2
|
A3
|
A4
|
собственный вектор
|
вес
|
| A1
|
1,000
|
7,000
|
0,500
|
8,000
|
2,300
|
0,480
|
| A2
|
0,143
|
1,000
|
0,125
|
3,000
|
0,481
|
0,100
|
| A3
|
2,000
|
8,000
|
1,000
|
0,200
|
1,337
|
0,279
|
| A4
|
0,125
|
0,333
|
5,000
|
1,000
|
0,676
|
0,141
|
| 4,795
|
1,000
|
Проверим согласованность матрицы:
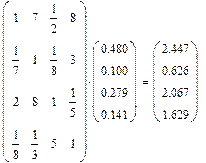
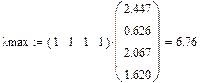
n = 4
L = 0,925
R = 0,900
T = 1,027 > 0,1 – матрица не согласована.
Альтернативы относительно критерия
k
2
| Альтернативы
|
A1
|
A2
|
A3
|
A4
|
собственный вектор
|
вес
|
| A1
|
1,000
|
4,000
|
6,000
|
8,000
|
3,722
|
0,654
|
| A2
|
0,250
|
1,000
|
8,000
|
0,143
|
0,731
|
0,129
|
| A3
|
0,167
|
0,125
|
1,000
|
3,000
|
0,500
|
0,088
|
| A4
|
0,125
|
7,000
|
0,333
|
1,000
|
0,735
|
0,129
|
| 5,688
|
1,000
|
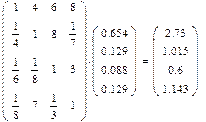
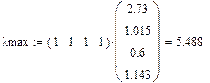
n = 4
L = 0,495
R = 0,900
T = 0,550 > 0,1 – матрица не согласована.
Альтернативы относительно критерия
k
3
| Альтернативы
|
A1
|
A2
|
A3
|
A4
|
собственный вектор
|
вес
|
| A1
|
1,000
|
4,000
|
0,111
|
8,000
|
1,373
|
0,282
|
| A2
|
0,250
|
1,000
|
1,000
|
2,000
|
0,841
|
0,173
|
| A3
|
9,000
|
1,000
|
1,000
|
3,000
|
2,280
|
0,468
|
| A4
|
0,125
|
0,500
|
0,333
|
1,000
|
0,380
|
0,078
|
| 4,873
|
1,000
|
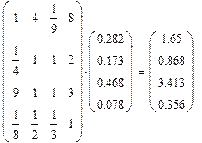
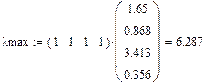
n = 4
L = 0,760
R = 0,900
T = 0,844 > 0,1 – матрица не согласована.
Альтернативы относительно критерия
k
4
| Альтернативы
|
A1
|
A2
|
A3
|
A4
|
собственный вектор
|
вес
|
| A1
|
1,000
|
4,000
|
6,000
|
8,000
|
3,722
|
0,637
|
| A2
|
0,250
|
1,000
|
3,000
|
2,000
|
1,107
|
0,189
|
| A3
|
0,167
|
0,333
|
1,000
|
3,000
|
0,639
|
0,109
|
| A4
|
0,125
|
0,500
|
0,333
|
1,000
|
0,380
|
0,065
|
| 5,848
|
1,000
|
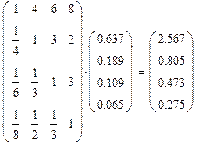
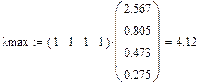
n = 4
L = 0,041
R = 0,900
T = 0,046 < 0,1 – матрица согласована.
Альтернативы относительно критерия
k
5
| Альтернативы
|
A1
|
A2
|
A3
|
A4
|
собственный вектор
|
вес
|
| A1
|
1,000
|
0,250
|
6,000
|
8,000
|
1,861
|
0,402
|
| A2
|
4,000
|
1,000
|
0,333
|
2,000
|
1,278
|
0,276
|
| A3
|
0,167
|
3,000
|
1,000
|
3,000
|
1,107
|
0,239
|
| A4
|
0,125
|
0,500
|
0,333
|
1,000
|
0,380
|
0,082
|
| 4,626
|
1,000
|
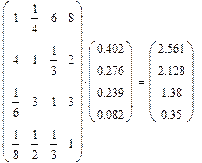
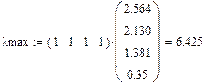
n = 4
L = 0,808
R = 0,900
T = 0,898 > 0,1 – матрица не согласована.
2. Определим наилучшую альтернативу-поставщика, с которым следует продлить договор.
VA
1
= 0,489
VA
2
= 0,143
VA
3
= 0,249
VA
4
= 0,119
Наилучшая альтернатива A1, следовательно, необходимо продлить договор с первым поставщиком.
Заключение
Данная курсовая работа состоит из двух частей:
1. Раздел I «Сетевые модели».
2. Раздел II «Использование метода анализа иерархий для организации поставок».
В 1 разделе рассматривалась задача о минимизации протяженности дорог между 7-ю населенными пунктами. В итоге была построена ориентированная сеть с начальным и конечным узлами. Построено минимальное остовное дерево, сумма весов ребер (протяженность дорог) которого составила 25 км.
Рассмотрена задача о минимизации времени в пути автотранспорта из начального узла в конечный узел сети, который составил 25 часов.
Найден максимальный поток для сети газопровода, составляющий 13 куб.ед., а также в результате расчетов выявлены «узкие» участки газопровода.
Во 2 разделе рассматривалась задача, в которой предприятию необходимо было решить вопрос о продлении договора на поставку с одним из поставщиков, основываясь на результатах работы по уже заключенным договорам.
После решения данной задачи была выбрана наилучшая первая альтернатива, в которой говорится, что надежнее продлить договор с первым поставщиком.
Литература
1. Шикин Е.В., Шикина Г.Е. Исследование операций: учеб. – М.: «Издательство Проспект»,2006.
2. Таха Хемди А. Введение в исследование операций. – М. Издательский дом «Вильямс», 2005.
3. Экономико-математическое моделирование: учебник под общ.ред. И.Н.Дрогобыцкого. – М. «Экзамен», 2006.
4. Ларичев О.И. Теория и методы принятия решений: - М.: Логос, 2003.
5. Тимашков П.С. Математические методы принятия решений: Учеб.пособие МГУПЭСИ – М., 2003.
6. Лагоша Б.А. Моделирование микроэкономических процессов и систем в инвестиционной деятельности : Учеб.пособие. – М.: Изд-во МГОУ, 2007.
7. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: - М.: Финансы и статистика, 2002.
8. Математические методы и модели исследования операций: учеб. Под ред. В.А.Колемаева. – М.: ЮНИТИ – ДАНА, 2008.
|