Курсова робота
на тему:
«Факторіальні кільця та їх застосування»
Вступ
Завдання алгебри є вивчення алгебраїчних структур. Безперечно, алгебра вивчає далеко не всі алгебраїчні структури. Можна побудувати чимало прикладів алгебраїчних структур, але в переважній більшості вони не матимуть ніяких застосувань ні в теорії, ні в практиці, а «теорія» таких структур складатиметься з означень і тривіальних наслідків з них. Такі структури, очевидно, не можуть бути об'єктом вивчення.
У процесі розвитку математики виділилася й стала докладно вивчатися невелика кількість основних типів алгебраїчних структур, алгебраїчні операції в яких за своїми властивостями більш-менш близькі до операцій додавання і множення чисел. Найважливішими серед різних алгебраїчних структур є група, кільце, поле, лінійний простір, лінійна алгебра. Вивчення властивостей саме цих алгебраїчних структур, опис їх будови і зв'язків між ними й іншими основними математичними об'єктами є одним з найважливіших завдань алгебри на сучасному етапі її розвитку.
У цій роботі буде детально розглянуто властивості та особливості таких алгебраїчних структур, як кільця. А саме, розглядатимуться кільця, які є факторіальними, тобто кільця, що є областю цілісності і будь-який їхній елемент, відмінний від нуля і дільників одиниці, однозначно (з точністю до дільників одиниці і порядку множників) розкладається на добуток простих множників. Зокрема будуть досліджуватись кільця головних ідеалів, евклідові кільця, кільця многочленів від однієї та від кількох змінних.
Кожний розділ теоретичного матеріалу супроводжується задачами, в розв’язанні яких підтверджуються на практиці теореми та властивості, які були доведені в теоретичній частині, та розглядаються окремі конкретні випадки, які допомагають краще зрозуміти той чи інший нюанс тієї чи іншої теми зокрема та теорії кілець в цілому.
1. Кільця: означення та приклади
Означення Непорожня множина K на якій визначено дві бінарні алгебраїчні операції «+» і «·» називається кільцем, якщо виконуються умови:
1. "a, b [a+b=b+a];
2. "a, b, c [(a+b)+c=a+(b+c)];
3. $θ,"a [a+θ=a];
4. "a $ã [a+ã=θ];
5. "a, b, c [(ab) c=a(bc)];
Реклама

6. "a, b, c [(a+b) c=ac+bc];
7. "a, b, c [c (a+c)=ca+cb];
Якщо операція множення комутативна, то кільце комутативне. Перші чотири аксіоми означають, що відносно операції додавання кільце утворює адитивну абелеву групу.
Приклади кілець, що наводяться нижче свідчать про те, що система аксіом кільця несуперечлива.
№1 Множина цілих чисел Z є комутативне кільце відносно визначених у ній операцій додавання і множення. Справді, множина Z є абелева група по додаванню, операція множення чисел, як відомо, асоціативна, комутативна і дистрибутивна відносно операції додавання.
№2 Множина парних чисел є комутативне кільце відносно операцій додавання і множення чисел. Справді, ця множина є абельова група по додаванню, в ній визначена операція множення: добуток парних чисел є парне число, причому операція множення асоціативна, комутативна і дистрибутивна відносно операції додавання.
№3 Множина R всіх дійсних чисел, очевидно також є кільце відносно визначених у ній операцій додавання і множення.
№4 Множина K всіх чисел виду 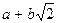 , де a і b – будь-які раціональні числа, є комутативне кільце відносно визначених у ній операцій додавання і множення. Справді, які б ми не взяли числа a1
+b1 , де a і b – будь-які раціональні числа, є комутативне кільце відносно визначених у ній операцій додавання і множення. Справді, які б ми не взяли числа a1
+b1
 і a2
+b2 і a2
+b2
 з множини K, їх сума (a1
+b1 з множини K, їх сума (a1
+b1
 )+(a2
+b2 )+(a2
+b2
 )=(a1
+a2
)+(b1
+b2
) )=(a1
+a2
)+(b1
+b2
) , добуток (a1
+b1 , добуток (a1
+b1
 ) (a2
+b2 ) (a2
+b2
 )= =(a1
a2
+2b1
b2
)+(a1
b2
+b1
a2
) )= =(a1
a2
+2b1
b2
)+(a1
b2
+b1
a2
) і різниця (a1
+b1 і різниця (a1
+b1
 ) – (a2
+b2 ) – (a2
+b2
 )=(a1
–a2
)+(b1
–b2
) )=(a1
–a2
)+(b1
–b2
) є числа виду є числа виду 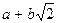 , тобто належать до множини K. Отже в множині K визначені операції додавання та множення і здійсненна обернена додаванню операція віднімання. Оскільки операції додавання і множення дійсних чисел асоціативні й комутативні, а елементи множини K є дійсні числа, то операції додавання і множення елементів множини K також асоціативні й комутативні. З цієї ж причини в множині K операція множення дистрибутивна відносно операції додавання. Отже, множина є комутативне кільце. , тобто належать до множини K. Отже в множині K визначені операції додавання та множення і здійсненна обернена додаванню операція віднімання. Оскільки операції додавання і множення дійсних чисел асоціативні й комутативні, а елементи множини K є дійсні числа, то операції додавання і множення елементів множини K також асоціативні й комутативні. З цієї ж причини в множині K операція множення дистрибутивна відносно операції додавання. Отже, множина є комутативне кільце.
До цього кільця належать, зокрема, всі раціональні числа (при b=0), а також число  (при а=0, b=1). В цьому прикладі замість числа (при а=0, b=1). В цьому прикладі замість числа  можна було взяти можна було взяти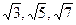 і інші. і інші.
№5 Множина, що складається з одного числа 0, очевидно, є кільце. Це кільце називають нульовим.
Означення Підмножина K´ кільця K називається його підкільцем, якщо вона сама утворює кільце відносно визначених в K операцій.
Теорема (критерій підкільця) K´ – підкільце кільця K тоді і тільки тоді, коли K´ÌK і "a, b [a, bÎK´Þ(a±b)ÎK´ÙabÎK´].
Реклама

Означення Характеристикою кільця K з одиницею називають найменше натуральне число n, для якого справджується рівність
ne=0
Якщо це можливо лише коли n=0, то говорять, що кільце K має нульову характеристику.
Зрозуміло, що всі числові кільця мають нульову характеристику.
Наведемо приклад кільця, яке має ненульову характеристику:
Z4
={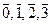 }, 4· }, 4·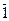 = =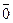 , n=4. , n=4.
Теорема Якщо кільце K має характеристику n, то для будь–якого aÎK справджується рівність na=0.
Доведення
ne=0 за умовою
na=n(ea)=(ne) a=0a=0.
Доведено.
Означення Комутативне кільце з одиницею e, в якому немає дільників нуля називається областю цілісності.
Задачі
№1
На множині R
задані операції:
aÅb=a+b+1,
aÄb=a+b+ab,
де +, - звичайні арифметичні операції. Довести, що алгебра (R,Å,Ä), буде областю цілісності.
Доведення.
Властивості кільця перевіряються безпосередньою перевіркою. Перевіримо дистрибутивність
(aÅb)Äc=aÄcÅaÄb.
Нехай A=(aÅb)Äc, B=aÄcÅaÄb, тоді
A=(aÅb)Äc=(a+b+1)Äc=a+b+1+c+ac+ab+c=a+b+2c+ac+bc+1,
B=aÄcÅaÄb=(a+c+ac)+(b+c+bc)=a+c+ac+b+c+bc+1=a+b+2c+ac+bc+1,
Отже, A=B.
Перевіримо існування нульового елемента
aÅq=a,
a+q+1=a,
q=–1 – нульовий елемент.
Перевіримо існування симетричного елемента
aÅã=q,
a+ã+1=–1,
ã=–2-a – протилежний елемент.
Отже, алгебра (R,Å,Ä) буде комутативним кільцем. Тепер з’ясуємо наявність одиниці.
aÄe=a
a+e+ae=a,
e (1+a)=0,
e=0 – одиничний елемент.
З’ясуємо чи існують дільники 0.
aÄb=–1, a≠–1, b≠–1,
a+b+ab=–1,
a+1+b (a+1)=0,
(a+1) (1+b)=0.
Оскільки a≠–1, b≠–1 і a, bÎR,
то дільників нуля немає.
Це означає, що K – область цілісності.
Доведено.
№2
Довести, що множина Z[ ] усіх чисел виду a+b ] усіх чисел виду a+b , де a і b – цілі числа, є кільцем відносно звичайних операцій додавання і множення. , де a і b – цілі числа, є кільцем відносно звичайних операцій додавання і множення.
Доведення.
Застосуємо прийом, який дає змогу скоротити процес доведення. Якщо треба довести, що деяка непорожня множина K1
є кільцем, то її поміщають (якщо це можливо) в якесь відоме кільце K. Тоді треба лише довести, що K1
є підкільце кільця K, звідки випливає, що K1
– кільце.
Оскільки Z[ ] є підмножиною, наприклад, кільця всіх дійсних чисел R
, то доведемо, що Z[ ] є підмножиною, наприклад, кільця всіх дійсних чисел R
, то доведемо, що Z[ ] – підкільце кільця R
. Застосуємо критерій підкільця.Насамперед, покажемо, що Z[ ] – підкільце кільця R
. Застосуємо критерій підкільця.Насамперед, покажемо, що Z[ ]≠Ø. Це справді так, бо, наприклад, 0=0+0 ]≠Ø. Це справді так, бо, наприклад, 0=0+0 ÎZ[ ÎZ[ ]. Нехай тепер t=a+b ]. Нехай тепер t=a+b , s=c+d , s=c+d , де a, b, c, d ÎZ
, t, s ÎZ[ , де a, b, c, d ÎZ
, t, s ÎZ[ ]. ].
Покажемо, що (t+s)ÎZ[ ], (t–s)ÎZ[ ], (t–s)ÎZ[ ], tsÎZ[ ], tsÎZ[ ]. ].
Справді, t±s=(a+b )±(c+d )±(c+d )=(a±c)+(b±d) )=(a±c)+(b±d) ÎZ[ ÎZ[ ], оскільки (a±с)ÎZ, (b±d)ÎZ. Аналогічно для добутку дістанемо ts=(a+b ], оскільки (a±с)ÎZ, (b±d)ÎZ. Аналогічно для добутку дістанемо ts=(a+b )±(c+d )±(c+d )=(ac+3bd)+(ad+bc) )=(ac+3bd)+(ad+bc) ÎZ[ ÎZ[ ], оскільки для цілих чисел a, b, c, d, 3 маємо ac, 3bd, ad, bcÎZ
. ], оскільки для цілих чисел a, b, c, d, 3 маємо ac, 3bd, ad, bcÎZ
.
Отже, Z[ ] – підкільце кільця дійсних чисел R
, а тому Z[ ] – підкільце кільця дійсних чисел R
, а тому Z[ ] – кільце. ] – кільце.
Доведено.
2. Ідеали кільця
2.1 Поняття ідеалу
В теорії подільності цілих чисел, а також в загальній теорії подільності в кільцях, важливу роль відіграє теорема про можливість і однозначність розкладу елемента (числа) в добуток простих множників. Виявляється в деяких кільцях розклад елемента на добуток простих множників не однозначний.
Наприклад, 60=2·30=6·10, а 2, 6, 30, 10 – прості елементи в Z2
Один і той же елемент в різних кільцях може бути простим і складеним.
Наприклад, 17 в Z[i] – складене 17=(4-i) (4+i).
Щоб з’ясувати, в яких кільцях справджується загальна теорема про існування і єдиність розкладу елемента в добуток простих множників, треба узагальнити поняття подільності елементів, що робиться за допомогою ідеалу.
Означення Непорожня множина I кільця K називається його ідеалом, якщо вона замкнена відносно віднімання і множення на довільний елемент кільця.
Переконаємося, що ідеал І замкнений відносно операції додавання. Справді із замкнутості відносно операції віднімання випливає, що 0ÎА (а–а=0), – еÎІ і поряд з кожним bÎI I'(–b) – b=–eb. Тому з кожним елементом a–b містить a – (–b)=a+b. (a+b)ÎI.
Звідси випливає, що ідеал І кільця К є його підкільцем. Проте не всяке підкільце кільця буде його ідеалом.
Розглянемо деякі приклади:
№1 К–ідеал самого себе. Цей ідеал називається одиничним. Позначається Іе
.
№2 Кожне кільце містить підкільце {0}, яке теж буде ідеалом кільця К. Цей ідеал називається нульовим. Позначається І0
.
Іе
та І0
– тривіальні ідеали. В розумінні відношення включення Іе
– найбільший, а І0
– найменший серед усіх ідеалів кільця.
Означення Ідеал І кільця К називається головним, якщо він складається з усіх елементів ка кільця К, аÎК, кÎК. Говорять, що він породжений елементом а. Позначають (а).
Наприклад, ідеал Z2
кільця Z буде головним, він породжений елементом 2 або –2.
2.1 Операції над ідеалами
Теорема Перетин ab ідеалів a, bÎK є ідеалом кільця K.
Доведення.
З того, що a, bÎI1
ÇI2
випливає, що abÎI1
, abÎI2
. Так як I1
та I2
–ідеали, то (a–b)ÎI1
, (a–b)ÎI2
Þ (a–b)ÎI1
ÇI2
. aÎI1
ÇI2
Þ aÎI1
, aÎI2
.
kÎK Þ kaÎI1
, kaÎI2
, kaÎI1
ÇI2
.
Отже, I1
ÇI2
ÎK.
Доведено.
Слід зауважити, що об’єднання ідеалів не завжди буде ідеалом кільця. Ця властивість поширюється на перетин n ідеалів.
Операції додавання й множення підмножин кільця можна, звичайно, застосувати до ідеалів.
Означення Сумою ідеалів I1
, I2
кільця K називається множина I1
+I2
, яка визначається рівністю
I1
+I2
={a+bï aÎI1
, bÎI2
}.
Означення Добуток ідеалів I1
I2
кільця К теж буде ідеалом кільця К.
Нехай а і b – довільні ідеали кільця К.
Теорема
2
. Сума а + b
ідеалів a
і b
кільця К
є ідеал цього кільця.
Доведення.
Справді, сума (а1
+b1
) + (a2
+ b2
) будь-яких двох елементів a1
+b1
і a2
+b2
множини a+b
належить до a+b
, оскільки (a1
+a2
)Îa
, (b1
+b2
)Îb
, і елемент – (а+b) = (–а) + (–b), протилежний довільно вибраному елементу (a+b)Î(a+b),
також належить до a+b
, бо (–a)Îa
, (–b)Îb
.
Отже, а + b
є підгрупа адитивної групи кільця K
. Крім того, для будь-яких елементів a+bÎa+b
і хÎK
x (a+b)=xa+xbÎa+b
і (a+b) x=ax+bxÎa+b
.
Цим теорему доведено.
Теорема 3.
Добуток ab
ідеалів а
і b
кільця К
. також є ідеал кільця К
.
Доведення.
Справді, сума 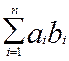 + +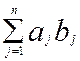 будь-яких двох елементів множини аb
є, очевидно, елемент цієї самої множини, і елемент будь-яких двох елементів множини аb
є, очевидно, елемент цієї самої множини, і елемент 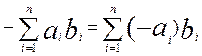 , протилежний довільно вибраному елементу , протилежний довільно вибраному елементу 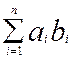 Îab
, належить до ab
. Крім того, для будь-яких Îab
, належить до ab
. Крім того, для будь-яких
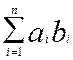 Îab
і xÎK Îab
і xÎK  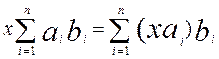 Îab
й
Îab
й 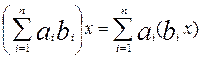 Îab
. Îab
.
Цим теорему доведено.
Таким чином, у множині ідеалів кільця К
здійсненні операції додавання й множення. Операція додавання ідеалів – асоціативна і комутативна, а операція множення – асоціативна. Якщо кільце К
– комутативне, то операція множення ідеалів також комутативна.
Задачі
№1
Нехай K1
– підкільце кільця K. Довести, що K1
ÇI –ідеал кільця K1
.
Доведення.
Введемо позначення D=K1
ÇI. Покажемо спочатку, що ідеал I, як і будь–який ідеал, містить нуль–елемент кільця K. Справді, оскільки I≠Ø, то в I існує хоч один елемент а. Тоді згідно з першим пунктом означення ідеалу, елемент а–а, тобто 0, теж належить ідеалу I. Оскільки 0ÎK1
, 0ÎI, то 0ÎD і тому D≠Ø.
Якщо a, bÎD, то a, bÎK1
і a, bÎI. Згідно з означенням ідеалу і критерієм підкільця, a±bÎI, a±bÎK1
, а тому a±bÎD.
Нехай aÎD, bÎK1
. Покажемо, що ab і ba належать D. Справді, оскільки DÍK1
, то a, bÎK1
і за критерієм підкільця K1
маємо, що
ab, ba ÎK1
. (1)
Оскільки DÍI, а I – ідеал кільця K, то для будь–якого елемента aÎDÍI і будь–якого елемента bÎK1
ÎK маємо, що
ab, baÎI. (2)
З включень (1) і (2) випливає, що
ab, baÎK1
ÇI=D.
Отже, D=K1
ÇI –ідеал кільця K1
.
Доведено.
№2
Чи є ідеалом (лівим або правим) така підмножина
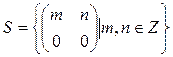
в кільці M (2, Z).
Розв’язання
Перевіримо чи буде множина S лівим ідеалом
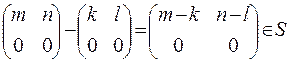
Перевіримо множення з ліва
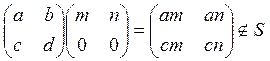
Отже, дана підмножина лівим ідеалом кільця M (2, Z).
Перевіримо чи буде правим ідеалом
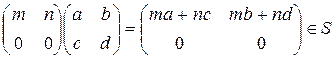
Отже правим ідеалом буде.
Відповідь:
є правим ідеалом.
3. Факторіальні кільця
3.1 Кільця головних ідеалів та евклідові кільця
3.1.1 Подільність в області цілісності
В теорії кілець особливої уваги заслуговують кільця, які за своїми властивостями досить близькі до кільця цілих чисел. Зокрема, для цих кілець можна розвинути теорію подільності, аналогічну теорії подільності цілих чисел. Ці кільця дістали назву кілець головних ідеалів. Вивченням їх ми і будемо займатись. Але спочатку викладемо деякі загальні відомості, що стосуються подільності в області цілісності з одиницею.
Нехай R
– область цілісності з одиницею. Оскільки область цілісності – комутативне кільце, то в ній поняття правого і лівого дільника елемента збігаються і тому означення подільності формулюється так:
Означення 1.
Якщо для елементів а і b області цілісності R
в R
існує такий елемент с, що а == bс, то говорять, що а ділиться на b або b ділить а і пишуть відповідно аM b; b/а або а == 0 (mod b).
Як бачимо, означення 1 є поширенням на область цілісності означення подільності в кільці цілих чисел, яке є конкретним прикладом області цілісності.
З означення 1 випливають такі властивості подільності в області цілісності:
1. "(a, b, cÎR
) [aM bÙbM cÞaM c].
2. "(a, b, cÎR
) [aM cÙbM cÞ(a+b)M c Ù(a-b)M c].
3. "(a, b, cÎR
) [aM b Þ acM b].
4. "(a1,
b1,
a2,
b2,…
, an,
bn,
cÎ R
) [a1
M cÙa2
M c Ù… Ùan
M c Þ (a1
b1
+a2
b2
+ … + +an
bn
) M c].
Ці властивості, як легко бачити, є поширенням на область цілісності відповідних властивостей подільності в кільці цілих чисел.
5. Кожен елемент аÎR
ділиться на будь-який дільник ε одиниці е. Справді, а = ε (ε-1
а) і, отже, ε/а.
6. Якщо а ÎR
ділиться на bÎR,
то а ділиться і на bε, де ε – будь-який дільник одиниці.
Справді, з рівності а = bс випливає рівність а == bε (ε-1
с) і, отже, bε/а.
7. Кожен з дільників одного з елементів а ÎR
і aεÎR
де ε – будь-який дільник одиниці, є дільником і іншого.
Справді, з рівності а = сg випливає рівність aε == с (εg), а з рівності аε = сq – рівність а == с (ε-1
q). Отже, якщо с/а, то с/аε, і навпаки.
Всюди далі будемо розглядати елементи області цілісності R
, відмінні від нуля.
Означення 2.
Елементи а і b області цілісності R
називаються асоційованими, якщо кожен з них є дільником іншого:
а = bс, b= аd. (1)
З рівностей (1) випливає, що а = а (сd). Звідси, скоротивши обидві частини рівності на а≠0, дістаємо сd = 1. Отже, с і d є дільники одиниці. Таким чином, якщо а і b – асоційовані елементи, то b = аε, де ε – деякий дільник одиниці. З другого боку, який би ми не взяли дільник одиниці ε, елементи а і аε асоційовані між собою, оскільки а = (аε) ε-1
.
Означення 2'.
Елементи а і b області цілісності R
називаються асоційованими, якщо b= аε, де ε – деякий дільник одиниці.
В кільці цілих чисел, наприклад, асоційованими є кожні два числа т і – т.
Якщо а і b – асоційовані елементи, тобто а = bс і b = аd, то (а) Í (b) і (b) Í (а) і, отже, (а) = (b).
Таким чином, два асоційовані елементи а і b породжують той самий головний ідеал.
Нехай а і b – довільні елементи області цілісності R
.
Означення 3.
Елемент сÎR
називається спільним дільником елементів а і b, якщо кожен з цих елементів ділиться на с. За властивістю 5, всі дільники одиниці е області цілісності R
є спільними дільниками елементів а і b. Але в елементів а і b можуть бути й інші спільні дільники. Ми хочемо ввести поняття найбільшого спільного дільника цих елементів. Означення НСД двох цілих чисел, за яким найбільшим спільним дільником називають найбільший із спільних дільників, поширити на область цілісності не можна, оскільки в довільній області цілісності R
немає відношення порядку. Проте ми знаємо й інше означення НСД двох чисел, а саме: НСД двох чисел називають такий спільний дільник цих чисел, який ділиться на будь-який інший їхній спільний дільник. Саме це означення ми й поширимо на область цілісності.
Означення 4.
Найбільшим спільним дільником елементів а і b області цілісності R
називається такий спільний дільник цих елементів, який ділиться на будь-який інший їхній спільний дільник.
Щоб зазначити, що d є найбільший спільний дільник елементів а і b, пишуть а=(а, b).
Якщо також d' = (а, b), то елементи d і d' діляться один на одного і, отже, вони асоційовані. З другого боку, якщо d = (а, b) і ε – будь-який дільник одиниці, то, очевидно, dе = (а, b). Як бачимо, найбільший спільний дільник елементів а і b визначається з точністю до множника ε, що є дільником одиниці.
Означення 5.
Елементи а, bÎR
називаються взаємно простими, якщо вони не мають спільних дільників, відмінних від дільників одиниці, тобто якщо (а, b) = 1.
Нехай ε – будь-який дільник одиниці і а – довільний елемент області цілісності R
. Тоді а = аε• ε-1
. З цієї рівності випливає, що всі елементи, асоційовані з елементом а, і всі дільники одиниці ε дільниками елемента а. Їх називають тривіальними, або невласними, дільниками елемента а. Всі інші дільники елемента а, тобто дільники, відмінні від аε і ε, якщо такі існують, називають нетривіальними, або власними. Так, в кільці цілих чисел Z
тривіальними дільниками числа 10 є числа ±1, ±10 і нетривіальними – числа ±2, ±5.
Означення 6.
Елемент аÎR
називається нерозкладним, або простим, якщо він не є дільником одиниці й не має нетривіальних дільників; елемент аÎR
називається розкладним, або складеним, якщо він має нетривіальні дільники.
Інакше кажучи, елемент аÎR
називається розкладним, якщо його можна записати у вигляді добутку а = bс двох нетривіальних множників b і с; він називається нерозкладним, якщо його не можна записати у вигляді добутку двох нетривіальних дільників, тобто якщо з а = bс завжди випливає, що один з множників b і с є дільник одиниці, а інший – асоційований з а. Так, у кільці цілих чисел Z
нерозкладними є числа ±2, ±3, ±5,… (тобто числа прості й протилежні простим); всі інші числа, відмінні від ±1, – розкладні.
Наведемо такі дві властивості нерозкладних елементів.
1. Якщо елемент рÎR
нерозкладний, то і будь-який асоційований з ним елемент рε також нерозкладний. Ця властивість випливає з властивості 7 подільності елементів області цілісності R
.
2. Якщо а – будь-який, а р – нерозкладний елемент з R
, то або а ділиться на р, або а і р – взаємно прості.
Справді, якщо (а, р) = d, то d, як дільник нерозкладного елемента р, або є деякий дільник ε одиниці, або елемент вигляду рε. У першому випадку а і р взаємно прості, в другому – а ділиться на р.
Задачі
№1
Довести, що (-8+3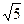 )M (1+2 )M (1+2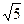 ) в кільці z [ ) в кільці z [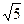 ]. ].
Доведення.
Поділимо ці гаусові числа, домноживши чисельник і знаменник частки на число спряжене із знаменником
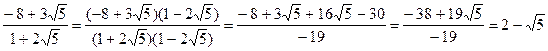 . .
Так як 2–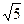 ÎZ[ ÎZ[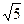 ], то (-8+3 ], то (-8+3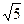 )M (1+2 )M (1+2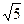 ). ).
Доведено.
№2
Довести, що в області цілісності К елементи 25–17 і 7- і 7- асоційовані, якщо К=z[ асоційовані, якщо К=z[ ]. ].
Доведення.
Асоційованість доводиться тим, що одне число ділиться на друге і навпаки.
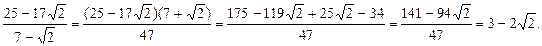 Оскільки 3–2 Оскільки 3–2 Î Z[ Î Z[ ], то (25–17 ], то (25–17 )M(7- )M(7- ). ).
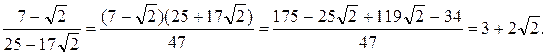
Бачимо, що і (7- )M(25–17 )M(25–17 ). ).
Отже, дані елементи асоційовані.
Доведено.
№3
Довести, що характеристикою області цілісності є або нуль, або просте число.
Доведення.
Нехай K – область цілісності, а е – одиниця кільця К. Якщо me≠0 для жодного натурального числа m1
, то характеристика кільця K дорівнює нулю.
Нехай тепер me=0 і m найменше натуральне число, що має цю властивість, тобто m – характеристика кільця K. Тоді m≠1, оскільки е≠0. Якщо m просте число, то твердження задачі доведено.
Нехай m складене число. Тоді існують натуральні числа s і t такі, що 1<s, t<m і m=st. Внаслідок комутативності кільця K маємо
0=me=(st) e=(se) (te).
Крім того, оскільки m – характеристика кільця K і s<m, t<m, то se≠0, te≠0 і тому (se) (te)=me≠0, бо K, як область цілісності, є кільцем без дільників нуля. Отже, ми прийшли до суперечності.
Тому характеристикою області цілісності є або нуль, або просте число.
Доведено.
3.1.2 Кільце головних ідеалів
Перейдемо тепер до вивчення кілець головних ідеалів.
Означення.
Кільцем головних ідеалів називається область цілісності з одиницею, в якій кожен ідеал є головний.
Найпростішим прикладом кілець головних ідеалів є кільце цілих чисел Z:
кільце Z,
як відомо, є область цілісності з 1 і, за теоремою, кожен його ідеал головний.
Кожне поле Р є кільце головних ідеалів. Справді, поле Р є областю цілісності з одиницею; якщо U є ненульовий ідеал поля Р, то разом з будь-яким своїм елементом а ≠ 0 він містить і елемент аa-1
= 1 і, отже, U = (1). Кільцем головних ідеалів є також кільце многочленів від змінної х з коефіцієнтами з поля Р
.
Звичайно, не кожна область цілісності з одиницею є кільцем головних ідеалів. Нижче ми наведемо приклади таких областей цілісності. А тепер займемося вивченням властивостей кілець головних ідеалів. Всюди далі вважатимемо, що R
– кільце головних ідеалів.
Теорема 1.
Будь-які два елементи а і b кільця головних ідеалів R
мають найбільший спільний дільник d, причому d= rа + sb, де r і s – деякі елементи кільця R
.
Доведення.
Якщо один з елементів а і b дорівнює нулю, то справедливість теореми очевидна. Нехай а і b – будь-які відмінні від нуля елементи кільця R
. Вони породжують ідеал (а, b), який складається з усіх елементів вигляду ха + уb, де х і у – будь-які елементи кільця R
. Оскільки R
– кільце головних ідеалів, то ідеал (а, b) є головний, тобто породжується деяким елементом dÎR
: (а, b) = (d).
Тому
d = rа + sb (r, sÎR
), (2)
а = gd, b = hd (g, hÎR
). (3)
З рівностей (3) випливає, що d є спільний дільник елементів а і b;
з рівності ж (2) випливає, що d ділиться на будь-який спільний дільник елементів а і b. Отже, а = (а, b).
Доведено.
Спираючись на теорему 1, доведемо твердження, яке є критерієм взаємної простоти двох елементів кільця головних ідеалів.
Теорема 2.
Елементи а і b кільця головних ідеалів R
взаємно прості тоді і тільки тоді, коли в кільці R
є такі елементи r і s, що rа +sb = 1.
Доведення.
Необхідність умови очевидна: якщо а і b – взаємно прості, тобто (а, b) = 1, то, за теоремою 1, в кільці R
існують такі елементи r і s, що rа + sb = 1. Доведемо достатність умови. Припустимо, що в кільці R
існують такі елементи r і s, що rа + sb = 1.
З цієї рівності випливає, що спільними дільниками елементів а і b можуть бути лише дільники одиниці і, отже, елементи а і b взаємно прості.
Доведено.
Теорема 3.
Якщо елемент аÎR
взаємно простий з кожним із елементів bÎR
і сÎК, то він взаємно простий і з добутком цих елементів.
Доведення
.
Оскільки а і b – взаємно прості, то, за теоремою 2, існують такі r, sÎR
, що
rа + sb = 1.
Помноживши цю рівність на с, дістаємо: а (rc) + (bс) s = с. З цієї рівності випливає, що кожен спільний дільник елементів а і bс буде дільником і елемента с. Але за умовою теореми спільними дільниками елементів а і с є лише дільники одиниці, тому і спільними дільниками a і bс будуть лише дільники одиниці й, отже, а і bс взаємно прості.
Теорема 4.
Якщо добуток елементів aÎR
і bÎR
ділиться на елемент с ÎR
, але а і с взаємно прості, то b ділиться на с.
Доведення.
Оскільки а і с – взаємно прості, то в кільці R
існують такі r і s, що
rа + sc = 1.
Помноживши цю рівність на b, дістаємо:
(аb) r+с (bs) = b.
Обидва доданки лівої частини останньої рівності діляться на с, а тому і права її частина b ділиться на с.
Теорема 5.
Якщо елемент а ÎR
ділиться на кожен з елементів bÎR
і сÎR
, які між собою взаємно прості, то а ділиться і на добуток bс.
Доведення.
Справді, за умовою теореми, а.:
b, тобто а = bg. Оскільки а M с, то bgM с. Але b і с взаємно прості, тому, за теоремою 4, g:
с, тобто g=cq.
Отже, а == (bс) q, тобто аMbс.
Доведено.
Теорема 6.
Якщо R
– кільце головних ідеалів і р – простий елемент цього кільця, то фактор-кільце R/(р)
є поле.
Доведення.
Одиничний елемент 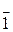 = 1 + (р) кільця R/(р)
відмінний від = 1 + (р) кільця R/(р)
відмінний від 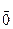 = (р). Справді, якби = (р). Справді, якби 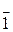 = = 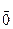 , то елемент 1 містився б в ідеалі (р) і тому р/1. Але елемент р не може бути дільником одиниці, оскільки він нерозкладний. Отже, в кільці R/(р)
є принаймні один відмінний від нуля елемент. , то елемент 1 містився б в ідеалі (р) і тому р/1. Але елемент р не може бути дільником одиниці, оскільки він нерозкладний. Отже, в кільці R/(р)
є принаймні один відмінний від нуля елемент.
Покажемо, що в кільці R/(р)
здійсненна операція ділення, крім_ділення на нуль, тобто що для будь-яких елементів 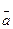 = a + (р) ≠ 0 і = a + (р) ≠ 0 і 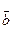 = =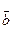 + (р) кільця R/(р)
рівняння + (р) кільця R/(р)
рівняння 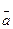 • • 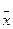 = = 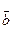 має в цьому кільці розв'язок. Справді, оскільки має в цьому кільці розв'язок. Справді, оскільки 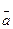 ≠ ≠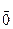 , то а не ділиться на р. Отже, за другою властивістю нерозкладних елементів, елементи а і р – взаємно прості, тобто (а, р) = 1. Тому, за теоремою 2, в кільці R
існують такі елементи r і s, що аr + рs = 1. Звідси , то а не ділиться на р. Отже, за другою властивістю нерозкладних елементів, елементи а і р – взаємно прості, тобто (а, р) = 1. Тому, за теоремою 2, в кільці R
існують такі елементи r і s, що аr + рs = 1. Звідси
аrb + рsb =b, аrb º b (тоd p),
і, отже, 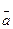 • • 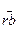 = = 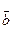 . Таким чином, . Таким чином, 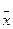 = =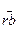 є розв'язком рівняння є розв'язком рівняння 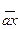 = =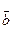 . .
Доведено.
Наслідок.
Якщо добуток кількох елементів кільця головних ідеалів R
ділиться на простий елемент рÎR
, то принаймні один із співмножників ділиться на р.
Доведення.
Припустимо, що добуток a1
• а2
•… • as
(ai
ÎR
) ділиться на нерозкладний елемент р ÎR
, тобто що a1
а2…
аs
Î (р).
Розглянемо елементи ai
= аi
+(р) (і =1, 2,…. s) і 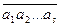 = a1
a2
…as
+(р). За означенням операції множення в кільці R/(р)
=
= a1
a2
…as
+(р). За означенням операції множення в кільці R/(р)
=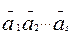 Оскільки a1
a2
…as
Î(р), то Оскільки a1
a2
…as
Î(р), то 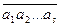 =
=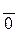 і, отже, і, отже, 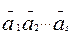 = = 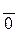 Звідси, оскільки, за теоремою 6, R/(р)
є поле, випливає, що для деякого m (1 < т < s) Звідси, оскільки, за теоремою 6, R/(р)
є поле, випливає, що для деякого m (1 < т < s) 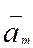 = =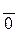 . Але . Але 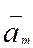 = =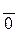 означає, що am
Î(p), тобто що am
M р. означає, що am
Î(p), тобто що am
M р.
Цим справедливість наслідку доведено.
Нашою метою буде тепер доведення твердження про можливість розкладу кожного елемента кільця головних ідеалів у добуток простих (нерозкладних) множників. Воно ґрунтується на такій лемі.
Лема.
В кільці головних ідеалів R
не існує нескінченної строго зростаючої послідовності ідеалів
U0
Ì
U1
Ì
U2
Ì
…
Ì
UN
Ì
….
(4)
Доведення.
Припустимо, що нескінченна строго зростаюча послідовність (4) існує. Позначимо символом b об'єднання всіх ідеалів послідовності (4). Множина b є ідеал кільця R
. Справді, якщо aєb
і bєb
, то а є елемент деякого ідеалу Us,
і b – деякого ідеалу Ul
. Тому а і b є елементи ідеалу Um
, де m – більший з індексів s і l. Отже, (а + b)є Um
Ìb
, (а – b)єUm
Ìb
і для будь-якого rєR
arєUm
Ìb
. Оскільки R
– кільце головних ідеалів, то ідеал b головний. Нехай b= (b). Елемент b, як елемент об'єднання ідеалів послідовності (4), належить до деякого ідеалу Uk
, а отже, і до кожного ідеалу Ui,
при і ≥k
Тому (b) = Uk
=Uk+1
= Uk+2
=…. А це суперечить нашому припущенню.
Доведено.
Теорема
7.
В кільці головних ідеалів R
кожен відмінний від нуля елемент, що не е дільником одиниці, розкладається в добуток простих множників.
Доведення.
Для кожного простого елемента кільця R
теорема справедлива: для простого елемента добуток, про який говориться в теоремі, складається з одного множника. Припустимо, що в кільці R
є відмінний від нуля елемент а, який не можна розкласти в добуток простих множників. Елемент а не простий і, отже, а = a1
a2
, де a1
і a2
– нетривіальні дільники елемента а.
Принаймні один з елементів a1
і a2
не можна розкласти в добуток простих множників, бо в противному разі і елемент а розкладався б у добуток простих множників. Не втрачаючи загальності міркувань, припустимо, що a1
не можна розкласти в добуток простих множників. Тоді a1
=a11
a12,
де a11
та a12
–нетривіальні дільники. Принаймні один з елементів a11
та a12
також не можна розкласти в добуток простих множників. Нехай цим елементом є a11
. Для елемента a11
міркування повторимо і т.д. Цей процес послідовного розкладу, очевидно, не може обірватися. Таким чином, ми дістанемо нескінченну послідовність елементів
а, a1
, a11
, a111
,…, (5)
у якій кожен наступний член є власним дільником попереднього.
Якщо ai+1
є власним дільником ai
, то (ai+1
)Ì(ai
), оскільки ai
=ai+1
r, де r – деякий елемент R
. Тому головні ідеали, породжені елементами послідовності (5), утворюють нескінченну строго зростаючу послідовність ідеалів
(а)Ì(a1
)Ì(a11
)Ì(a111
)Ì…,
а це суперечить доведеній вище лемі. Отже, наше припущення неправильне.
Доведено.
Покажемо тепер, що розклад, про який іде мова в теоремі 7, однозначний з точністю до порядку співмножників і до дільників одиниці.
Теорема
8.
Якщо
a =p1
p2
…pr
=q1
q2
…qs
є два розклади елемента а кільця головних ідеалів R
в добуток простих множників, то r=s і, при відповідній нумерації співмножників, справджуються рівності qi
=εi
pi
(і == 1, 2,…, r), де εi
– деякий дільник одиниці кільця R
.
Доведення.
Доводитимемо індукцією по r. При r = І справедливість твердження очевидна.
Справді, оскільки елемент а = р1
простий, то добуток q1
q2
…qs
може містити лише один множник q1=
p1
.
Припустимо, що теорема правильна для r – 1 (2 £ r), і доведемо, що в такому разі теорема справедлива й для r. Справді, оскільки
a =p1
p2
…pr
і a = q1
q2
…qs
то
p1
p2
…pr
=q1
q2
…qs
(6)
З рівності (6) випливає, що q1
q2
…qs
ділиться на p1
. Тому, за наслідком з теореми 6, принаймні один із співмножників q1,
q2,
…, qs
ділиться на pi
. Ми вважатимемо, що на p1
ділиться множник q1
: цього завжди можна досягти зміною нумерації множників q1,
q2,
…, qs.
Оскільки q1
– простий елемент і ділиться на простий елемент p1
, то q1
=e1
p1
, де e1
– деякий дільник одиниці кільця R
. Підставивши в рівність (6) e1
p1
замість q1
і скоротивши обидві частини одержаної рівності на р1
, дістанемо:
p2
p3
…pr
=(e1
q2
) q3
…qs.
Але, за індуктивним припущенням, r– 1 == s– 1 і при відповідній нумерації множників q1,
q2,
…, qr
:
q2
=e1
q2
=e2
p2,
q3
=e3
p3
, …, qr
=er
pr
,
де ei
– деякі дільники одиниці кільця R
. Тому r = s і при відповідній нумерації множників q1
, q2
, …, qr
:
q1
=e1
p1
, q2
=e1
–1
e2
p2
=e2
p2,
q3
=e3
p3
, …, qr
=er
pr
Доведено.
Зауважимо, що теореми 7 і 8 справедливі, зокрема, для кільця цілих чисел, яке є кільцем головних ідеалів.
Постає запитання: чи не можна теореми 7 і 8 поширити на клас областей цілісності більш широкий, ніж кільце головних ідеалів? Відповідь на це запитання в загальному випадку негативна. Є області цілісності, в яких не справджується теорема про розклад елементів області цілісності в добутки простих множників, а також області цілісності, в яких розклад елементів на прості множники хоч і можливий, але не однозначний. Наведемо приклади таких областей цілісності, не вивчаючи її докладно.
Нехай К – множина всіх дійсних чисел виду
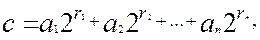
де n – будь-яке натуральне число, a1,
a2,…,
an
– будь-які цілі числа й r1
, r2
,…, rn
– будь-які числа виду 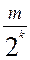 (m, k – цілі невід'ємні числа). Сума, різниця й добуток чисел такого виду – числа такого самого виду. Отже, К – кільце. При п = 1 і r1
=0 дістанемо с = а1
; тому К містить усі цілі числа, зокрема 1. Легко бачити, що кільце К є область цілісності. У цій області цілісності число 2 розкладається на множники так: (m, k – цілі невід'ємні числа). Сума, різниця й добуток чисел такого виду – числа такого самого виду. Отже, К – кільце. При п = 1 і r1
=0 дістанемо с = а1
; тому К містить усі цілі числа, зокрема 1. Легко бачити, що кільце К є область цілісності. У цій області цілісності число 2 розкладається на множники так:
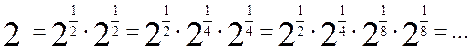
Можна довести, що числа виду 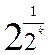 , де k – ціле невід'ємне число, не є дільниками одиниці в кільці К. Таким чином, число 2 не можна розкласти на прості множники в кільці К. , де k – ціле невід'ємне число, не є дільниками одиниці в кільці К. Таким чином, число 2 не можна розкласти на прості множники в кільці К.
Нехай тепер Q – множина всіх комплексних чисел виду 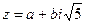 , де а і b – будь-які цілі числа. Сума, різниця й добуток чисел такого виду є, очевидно, числа такого самого виду. Отже, Q – кільце. При b = 0, z = а, а тому в Q містяться всі цілі числа. Отже, кільце Q є область цілісності. Можна довести, що в цій області цілісності кожне число розкладається на прості множники. Проте не можна стверджувати, що для цього кільця характерна однозначність розкладу на прості множники. Для числа 6, наприклад, у цьому кільці , де а і b – будь-які цілі числа. Сума, різниця й добуток чисел такого виду є, очевидно, числа такого самого виду. Отже, Q – кільце. При b = 0, z = а, а тому в Q містяться всі цілі числа. Отже, кільце Q є область цілісності. Можна довести, що в цій області цілісності кожне число розкладається на прості множники. Проте не можна стверджувати, що для цього кільця характерна однозначність розкладу на прості множники. Для числа 6, наприклад, у цьому кільці
існують такі два розклади: 6=2·3 і 6 = (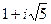 ) ( ) (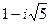 ). ).
Поряд з цим існують області цілісності, які не є кільцями головних ідеалів, проте в них справджуються теореми 7 і 8.
3.1.3 Факторіальність кільця головних ідеалів
Нашою метою являється узагальнення на кільці головних ідеалів теореми про існування й одиничність розкладу елементів кільця цілих чисел Z
на прості множники.
Означення
Говорять, що елемент а області цілісності K
має однозначний розклад на прості множники, якщо виконуються умови:
(1) існують у K
такі прості елементи рi
, що
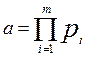 ; ;
(2) якщо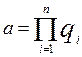 - інший розклад, у якому qi – прості елементи K
, то m=n і при відповідній нумерації рi
~ qi
для i=1,…, m. - інший розклад, у якому qi – прості елементи K
, то m=n і при відповідній нумерації рi
~ qi
для i=1,…, m.
Означення
Кільце називається факторіальним, якщо воно є областю цілісності і всякий відмінний від нуля необоротний елемент кільця має однозначний розклад на прості множники.
Відзначимо, що будь-яке поле є факторіальним кільцем, тому що не має відмінних від нуля необоротних елементів.
Теорема
Кільце головних ідеалів факторіальне.
Доведення.
Нехай K
– кільце головних ідеалів. Нам треба довести, що усякий відмінний від нуля необоротний елемент кільця має розкладання на прості множники. Припустимо, що існує в K
необоротний ненульовий елемент а, що нерозкладний на прості множники в Ж. Тоді елемент а є складеним. Отже, його можна подати у вигляді добутку двох власних дільників а=аi
bi
і (a)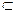 (ai
) (ai
)
Принаймні один із множників аi
, bi
, наприклад a1
, не має розкладу на прості множники. Отже, a1
можна подати у вигляді добутку двох власних множників:
a1
=a2
b2
, (a1
)=(a2
)
і т.д. Таким чином, існує нескінченний зростаючий ланцюжок
(a)Ì(a1
)Ì(a2
)Ì…
ідеалів кільця K
, що неможливо, бо за твердженням зростаючий ланцюжок не може бути нескінченним. Отже, усякий необоротний відмінний від нуля елемент кільця K
має розклад на прості множники.
Доведемо однозначність розкладу на прості множники. Якщо a – простий елемент, то теорема вірна. Припустимо, що теорема вірна для елементів, представлених у вигляді добутку n простих множників, і доведемо, що тоді вона вірна для елементів, представлених у вигляді добутку n+1 простих множників. Нехай дані будь-які два розклади елемента a на прості множники:
a=p1
…pn
pn+1
=q1
…qs
qs+1
(1)
Простий елемент рn+1
ділить добуток q1
…qs
qs+1
. Отже, він ділить хоча б один із множників q1
…qs
qs+1
, наприклад qs+1
. Так як рn+1
і qs+1
– прості, тo qs+1
=upn+1
, де u – оборотний елемент кільця. Скорочуючи обидві частини рівності (1) на рn+1
, маємо
p1
…pn
=q1
… (uqs
).
Отже, по індуктивному припущенню, n=s і при відповідній нумерації рi
~ qi
для i=1,…, n. Крім того, рn+1
~ пn+1
.
Доведено.
Задачі
№1
Довести, що число 4 в кільці Z[ ] неоднозначно розкладається в добуток простих множників. ] неоднозначно розкладається в добуток простих множників.
Доведення.
Знайдемо спочатку дільники одиниці в Z[ ]. Нехай a+b ]. Нехай a+b , c+d , c+d – дільники одиниці, a, b, c, d ÎZ
. Тоді – дільники одиниці, a, b, c, d ÎZ
. Тоді
(a+b ) (c+d ) (c+d )=1. )=1.
Знайдемо норму обох частин цієї рівності:
Nr (a+b )=(a2
+3b2
). )=(a2
+3b2
).
Маємо
(a2
+3b2
) (c2
+3d2
)=1. (1)
Рівність (1) виконується, якщо
a2
+3b2
=c2
+3d2
=1. (2)
Рівність (2), в свою чергу, виконується при a=±1, b=0, c=±1, d=0. Отже, в кільці Z[ ] лише 2 дільники одиниці: 1, –1. ] лише 2 дільники одиниці: 1, –1.
Доведемо, що для числа 4 в кільці Z[ ] є два різних розклади в добуток простих множників: ] є два різних розклади в добуток простих множників:
4=2·2=(1+ ) (1– ) (1– ). ).
Для цього покажемо, що 2, 1+ , 1– , 1– є прості числа в Z[ є прості числа в Z[ ], а пари чисел 2, 1+ ], а пари чисел 2, 1+ та 2, 1– та 2, 1– не є асоційованими. не є асоційованими.
Оскільки в кільці Z[ ] асоційовані числа відрізняються лише знаком, то покажемо, що 2, 1+ ] асоційовані числа відрізняються лише знаком, то покажемо, що 2, 1+ , 1– , 1– є прості числа в Z[ є прості числа в Z[ ]. ].
Якщо 2=(a+b ) (c+d ) (c+d ), то знайшовши норми від обох частин, дістанемо 4= (a2
+3b2
) (c2
+3d2
). ), то знайшовши норми від обох частин, дістанемо 4= (a2
+3b2
) (c2
+3d2
).
Число 4 розкладається в добуток натуральних чисел двома способами:
4=2·2=1·4.
Якщо a2
+3b2
=2, то b2
<1, тобто b=0. Тоді a2
=2, що неможливо для цілого числа a. Отже, a2
+3b2
=1 або a2
+3b2
=4. Якщо a2
+3b2
=1, то a+b – дільник одиниці. Якщо a2
+3b2
=4, то c2
+3d2
=1 і c+d – дільник одиниці. Якщо a2
+3b2
=4, то c2
+3d2
=1 і c+d – дільник одиниці. – дільник одиниці.
Отже, 2 є просте число в кільці Z[ ]. Оскільки Nr (1± ]. Оскільки Nr (1± )=4, то аналогічно доводять, що числа 1± )=4, то аналогічно доводять, що числа 1± є простими. є простими.
Отже, число 4 в кільці Z[ ] розкладається на прості множники двома різними способами. ] розкладається на прості множники двома різними способами.
Доведено.
3.1.4 Евклідові кільця, їх факторіальність
Порівняно з кільцями головних ідеалів більш близькими до кільця цілих чисел за своїми властивостями є кільця, в яких справедлива теорема, що є аналогом теореми про ділення з остачею в кільці цілих чисел. Ці кільця називають евклідовими. Вони означаються так:
Означення.
Область цілісності R
з одиницею називається евклідовим кільцем, якщо існує відображення φ множини відмінних від 0 елементів цієї області цілісності в множину цілих невід'ємних чисел N0
, тобто φ:R\{0}→N0
, яке задовольняє таку вимогу: для будь-яких елементів a, bÎR
, b¹0 в R
існують такі елементи q і r, що а =bq+r, причому або r= 0, або φ(r)<φ(b).
Кільце цілих чисел Z
– евклідове; відображення φ, про яке йде мова в означенні, задається так:
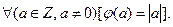
Евклідовим також є кільце многочленів від невідомого х з коефіцієнтами з поля Р.
Теорема 9.
Кожне евклідове кільце R
є кільцем головних ідеалів.
Доведення.
Нехай U – довільний ідеал евклідового кільця R
. Якщо U – нульовий ідеал, то U= (0). Припустимо, що ідеал U – відмінний від нульового. Тоді в U є елементи, відмінні від нуля. Серед відмінних від нуля елементів ідеалу U, очевидно, є такий елемент a0
, що φ(a0
)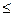 φ(a) для будь-якого ненульового елемента аÎU. За означенням евклідового кільця, для будь-якого елемента аÎU в кільці R
існують такі елементи q і r, що a=a0
q+r, причому, якщо r¹ 0, то φ(r)<φ(a0
). Але оскільки r=a-a0
qÎU, то можливість r¹0 виключається і тому r=0. Таким чином, a=a0
q і, отже, U є головний ідеал, породжений елементом а0
. φ(a) для будь-якого ненульового елемента аÎU. За означенням евклідового кільця, для будь-якого елемента аÎU в кільці R
існують такі елементи q і r, що a=a0
q+r, причому, якщо r¹ 0, то φ(r)<φ(a0
). Але оскільки r=a-a0
qÎU, то можливість r¹0 виключається і тому r=0. Таким чином, a=a0
q і, отже, U є головний ідеал, породжений елементом а0
.
Доведено.
Наслідок Будь–яке евклідове кільце факторіальне.
Наслідок Кільце Z цілих чисел є кільцем головних ідеалів і, значить, факторіальне.
Оскільки кожне евклідове кільце є кільцем головних ідеалів, то для елементів будь-якого евклідового кільця справедливі теореми 7 і 8. Зауважимо, що твердження, обернене твердженню 9, неправильне: існують кільця головних ідеалів, які не є евклідовими.
Нам уже відомо про існування найбільшого спільного дільника для будь-яких двох елементів а і b кільця головних ідеалів R
. А тепер поговоримо про те, як же відшукати цей найбільший спільний дільник. Методу, який би давав змогу відшукати найбільший спільний дільник будь-яких двох елементів а і b довільного кільця головних ідеалів R
, не існує. В евклідових же кільцях його можна відшукати за допомогою алгоритму Евкліда. Справді, нехай a0
і a1
будь-які відмінні від нуля елементи евклідового кільця R
і нехай φ(а0
) ³ φ(а1
). Тоді, за означенням евклідового кільця, в R
існують такі елементи q1,
a2
, що а0
= а1
q1
+а2
, причому або а2
= 0, або φ(а1
) > φ(а2
). Якщо а2
¹ 0, то в R
існують такі елементи q2
і a3
, що a1
= a2
q2
+a3
причому або а3
= 0 або φ(а2
)>φ(а3
). Якщо а3
¹ 0, то в R
існують такі елементи q3
i a4
, що а2
=а3
q3
+a4
і т.д.
Оскільки φ(а1
) > φ(а2
) > φ(а3
) >… > φ(аs-1
) >φ(аs
)>…, то цей процес послідовного ділення не може продовжуватись нескінченно: в противному разі множина цілих невід'ємних чисел φ(а1
) >
φ(а2
)>… > φ(аs
) >… не мала б найменшого числа. Отже, через кілька кроків ми дійдемо до ділення з остачею нуль: am-1
= аm
qm
. Таким чином, ми матимемо рівності
а0
= а1
q1
+а2
,
a1
= a2
q2
+a3
,
а2
=а3
q3
+a4
,
……………
am-3
=am-2
qm-2
+am-1
,
am-2
=am-1
qm-1
+am
,
am-1
=am
qm+1
.
Остання рівність означає, що аm
дільником am-1
. Оскільки кожен з доданків правої частини передостанньої рівності ділиться на аm
, то і її ліва частина ділиться на аm
, тобто аm
є дільником am-2.
Аналогічними міркуваннями ми доведемо, що аm
є дільником am-3
, am-4
,…, a4
, а3
, a2
, a1
, а0
. Отже, аm
є спільним дільником елементів ао
і а1
. Покажемо тепер, що аm
ділиться на будь-який спільний дільник елементів ао
і а1
. Нехай b – довільно вибраний спільний дільник aо
і a1
. Тоді з рівності ао
= a1
q1
+q2
випливає, що a2
ділиться на b, з рівності а1
= a2
q2
+ а3
випливає, що а3
ділиться на b і т.д. Нарешті, з рівності ат–2
= aт–1
qт–1
+ am
випливає, що am
ділиться на b. Таким чином, елемент аm
є спільним дільником елементів a0
і a1
і ділиться на будь-який спільний дільник цих елементів, тобто аm
є найбільшим спільним дільником елементів a0
i a1
.
Задачі
№1
Довести, що в 5кільці Z[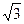 ] простими є такі елементи ] простими є такі елементи
а) 2;
б) –2;
в) 1+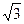 і; і;
г) 1–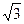 і; і;
Доведення
Знайдемо спочатку дільники одиниці в Z[ ]. ].
Нехай a+b , c+d , c+d – дільники одиниці, a, b, c, d ÎZ
. Тоді – дільники одиниці, a, b, c, d ÎZ
. Тоді
(a+b ) (c+d ) (c+d )=1. )=1.
Знайдемо норму обох частин цієї рівності:
Nr (a+b )=(a2
+3b2
). )=(a2
+3b2
).
Маємо
(a2
+3b2
) (c2
+3d2
)=1. (1)
Рівність (1) виконується, якщо
a2
+3b2
=c2
+3d2
=1. (2)
Рівність (2), в свою чергу, виконується при a=±1, b=0, c=±1, d=0. Отже, в кільці Z[ ] лише 2 дільники одиниці: 1, –1. ] лише 2 дільники одиниці: 1, –1.
а)
Зрозуміло, що 2¹0 і не є дільником одиниці в кільці Z[ ]. Використаємо норму і покажемо, що 2 – простий елемент в кільці Z[ ]. Використаємо норму і покажемо, що 2 – простий елемент в кільці Z[ ]. Оскільки Nr(2)=4, то, припустивши, що 2 є складене число, дістаємо ]. Оскільки Nr(2)=4, то, припустивши, що 2 є складене число, дістаємо
2=(a+b ) (c+d ) (c+d ), (3) ), (3)
де a+b , c+d , c+d не є дільниками одиниці і не є асоційованими з числом 2, a, b, c, d Î Z[ не є дільниками одиниці і не є асоційованими з числом 2, a, b, c, d Î Z[ ]. ].
З рівності (3) маємо
4=(a2
+3b2
) (c2
+3d2
) (4)
Для a, b, c, d Î Z ця рівність можлива тоді і тільки тоді, коли
a2
+3b2
=1, c2
+3d2
=4 (a)
або a2
+3b2
=4, c2
+3d2
=1 (b)
або a2
+3b2
=2, c2
+3d2
=2 (g)
В (a) і (b) дістаємо, що або a2
+3b2
або c2
+3d2
відповідно є дільником одиниці, що суперечить припущенню
Розглянемо (g) a2
+3b2
=2, a2
=2, а= 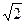 ÏZ. ÏZ.
Отже, цей випадок теж не можливий, бо a, b, c, d повинні належати Z.
Отже, 2 не може бути складеним числом. Оскільки 2¹0 і не є дільником одиниці, то 2 – просте число в кільці Z[ ]. ].
б)
Так як ми довели, що 2 – простий елемент кільця Z[ ], то можна стверджувати, що –2 теж просте, бо –2 є асоційованим з числом 2. ], то можна стверджувати, що –2 теж просте, бо –2 є асоційованим з числом 2.
в)
Очевидно, що 1+ ¹0 і не є дільником одиниці в кільці Z[ ¹0 і не є дільником одиниці в кільці Z[ ]. Використаємо норму і покажемо, що 1+ ]. Використаємо норму і покажемо, що 1+ є простим елементом. є простим елементом.
Оскільки Nr (1+ )=2, то, припустивши, що 1+ )=2, то, припустивши, що 1+ є складеним дістаємо є складеним дістаємо
1+ =(a+b =(a+b ) (c+d ) (c+d ), ),
де a+b , c+d , c+d не є дільником одиниці і не є асоційованим з числом 1+ не є дільником одиниці і не є асоційованим з числом 1+ , a, b, c, dÎZ. , a, b, c, dÎZ.
З цієї рівності маємо
(a2
+3b2
) (c2
+3d2
)=2.
Для цілих чисел a, b, c, dця рівність можлива лише, коли
a2
+3b2
=2, c2
+3d2
=1 або a2
+3b2
=1, c2
+3d2
=2
При цьому маємо, що або a2
+3b2
або c2
+3d2
відповідно є дільником одиниці, що суперечить припущенню. Отже, 1+ – простий елемент в кільці Z[ – простий елемент в кільці Z[ ]. ].
г)
Розглянемо число 1– . Знайдемо його норму . Знайдемо його норму
Nr (1– )=2 )=2
Так як Nr (1– )=Nr (1+ )=Nr (1+ )=2 і 1+ )=2 і 1+ – просте число, то і 1– – просте число, то і 1– – теж просте. – теж просте.
Доведено.
3.2 Кільце поліномів
3.2.1 Поняття кільця поліномів від однієї змінної
Нехай K
і L
– комутативні кільця з основними множинами К і L відповідно.
Означення.
Кільце L
називається простим розширенням кільця K
за допомогою елемента u, якщо виконуються умови:
(1) K
– підкільце кільця L;
(2) будь-який елемент a з L можна подати у вигляді
a=a0
+a1
u+ … +an
un
, де a0
, a1
,…, an
ÎK.
Запис L
= K[u]
означає, що кільце L
є просте розширення кільця K
за допомогою елемента u.
У цьому випадку основну множину кільця L
позначають також через К[u], L=K[u]
Означення.
Кільце L=K[u]
називається простим трансцендентним розширенням кільця K
, якщо виконується наступна умова:
(3) для будь-яких елементів a0
, a1
,…, an
множини К з рівності a0
+a1
u+ … +an
un
=0 випливають рівності a0
=0, a1
=0,…, an
=0.
Якщо L=K[u]
– просте розширення кільця K с допомогою u і u задовольняє умовам (3), то елемент u називається трансцендентним відносно K
.
Якщо K[u]
– просте трансцендентне розширення кільця K
за допомогою u, то кільце K[u]
називається також кільцем поліномів від u над K
, а елементи кільця K[u]
– поліномами від u над K
чи поліномами над K
.
Твердження.
Нехай K[u]
– просте трансцендентне розширення кільця K
за допомогою u. Тоді для будь-якого елемента а кільця K[u]
, якщо а=a0
+a1
u+ … +an
un
і а=a¢0
+a¢1
u+ … +a¢n
un
, де ai
, a¢i
ÎK, то ai
=a¢i,
то ai
=a¢i
для i=1,2,…, n.
Доведення.
Якщо
а=a0
+a1
u+ … +an
un
=a¢0
+a¢1
u+ … +a¢n
un
(ai
, a¢i
ÎK),
то a0
–a0
¢+(a1
–a1
¢) u+ … +(an
–an
¢) un
=0.
За умовою, елемент u являється трансцендентним відносно K
. Тому з (1) випливають рівності aі
–aі
¢=0 і aі
=aі
¢ для і=0,1,…, n.
Доведено.
Задачі
№1
Перевіримо, чи є кільцем множина К всіх многочленів з кільця Z[x], в яких вільний член ділиться на 5.
Розв’язання.
Нехай f(x)=an
xn
+ … +a1
x+5a0
,
g(x)=bm
xm
+ … +b1
x+5b0
, m³n.
Тоді
f(x)+g(x)=bm
xm
+ … +(an
+bn
) xn
+ … +(a1
+b1
) x+(5a0
+5b0
)=bm
xm
+ … +(an
+bn
) xn
+ … + +(a1
+b1
) x+5 (a0
+b0
),
f(x) – g(x)=(–bm
)xm
+ … +(an
–bn
) xn
+ … +(a1
–b1
) x+5 (a0
–b0
),
f(x)·g(x)=an
bm
xn+m
+ … +(5a1
b0
+5a0
b1
)+5·5a0
b0
.
Це означає, що f(x)+g(x), f(x) – g(x) і f(x)·g(x) також є елементами множини К. Отже, К є підкільцем кільця Z[x].
Відповідь:
Множина К утворює кільце.
№2
Довести, що для кожного многочлена f(x) з кільця Z[x] і для будь–яких цілих чисел a і b число f (a+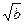 )+f (a– )+f (a–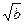 ) є цілим. ) є цілим.
Доведення.
Многочлени f (a+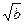 ) та f (a– ) та f (a–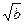 ) мають такий вигляд ) мають такий вигляд
f (a+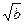 ) =an
(a+ ) =an
(a+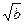 )n
+ … +a1
(a+ )n
+ … +a1
(a+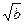 )+a0
, )+a0
,
f (a–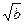 ) =an
(a– ) =an
(a–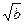 )n
+ … +a1
(a– )n
+ … +a1
(a–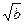 )+a0
. )+a0
.
Коли ми будемо додавати f (a+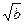 )+f (a– )+f (a–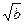 ) і підносити до степеня, то всі ) і підносити до степеня, то всі 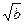 знищаться і залишаться лише цілі числа. Ми прийшли до того, що нам потрібно довести. знищаться і залишаться лише цілі числа. Ми прийшли до того, що нам потрібно довести.
Доведено.
3.2.2 Факторіальність кільця поліномів
Теорема.
Якщо кільце К
факторіальне, то і кільце поліномів К[x]
факторіальне.
Доведення.
Нехай К
– факторіальне кільце. Доведемо, що будь-який відмінний від нуля необоротний елемент кільця К[x]
однозначно з точністю до порядку співмножників і оборотних множників розкладемо в добуток простих множників в K[x]
. Спочатку доведемо можливість розкладання на прості множники. Нехай f – довільний ненульовий поліном з K[х]. Якщо f – поліном нульового ступеня, то fÎК. Оскільки кільце K
факторіальне, поліном f можна подати у вигляді добутку простих множників у К
і, значить, у К[x]
.Припустимо, що deg f =n>0, і всякий поліном, ступінь якого менше n, розкладемо в добуток простих множників. Нехай
(1) f=dg(x),
де dÎK, g(x) – поліном позитивного степеня, примітивний в К[х]
. Якщо поліном g незвідний над К
, то, розкладаючи в (1) множник а на прості множники, одержимо розкладання f на прості множники. Якщо ж поліном g(х) звідний в К[х]
, то його можна подати у вигляді добутку двох поліномів позитивного степеня, меншого, ніж n: g(x)=h(x)j(x).По індуктивному припущенню, h(х) і j(х) можна подати у вигляді добутку простих множників у К[x].
Отже, g, а в силу (1) і f також можна подати у вигляді добутку простих множників.
Доведемо єдиність розкладу. Нехай дані будь-які два розклади f на прості множники в K[x]
:
(2) f=p1
…pk
q1
…qs
=p1
¢…pr
¢q1
¢…qt
¢,
де pi
, pi
¢ÎK, qi
, qi
¢ – незвідні, а виходить, і примітивні поліноми позитивного степеня. З (2) випливає, що
(3) p1
…pk
~p1
¢…pr
¢ в K
;
(4)q1
…qs
~q1
¢…qt
¢ в K[x].
Оскільки кільце K
факторіальне, то з (3) випливає, що k=r і при відповідній нумерації
(5) pi
~pi
¢ в K
для i=1, 2, …, k
Далі, за наслідком 3.6, поліноми qi
і qi
¢ незвідні в кільці F[х]
. У силу факторіальності кільця F[х]
з (4) випливає, що s=t і при відповідній нумерації
qi
~ qi
¢ в F[х]
для i=1,…, s.
Поліноми qi
і qi
¢ незвідні в K[x]
і, значить, примітивні в K[х]
, крім того, ці поліноми асоційовані в F[x]
. Отже, вони асоційовані в K[x]
,
(6) qi
~ qi
¢ в K[х]
для i=1,…, s.
У силу (5) і (6) поліном f має однозначний розклад на прості множники в кільці K[x]
. Отже, показано, що кільце K[x]
факторіальне.
Доведено.
Задачі
№1
Довести, що множина I всіх многочленів кільця Z[x], вільний член яких дорівнює парному числу, є ідеалом Z[x]. Чи є цей ідеал головним?
Розв’язання.
Очевидно, що ця множина замкнена відносно віднімання та множення на довільний елемент кільця. Отже, ця множина буде ідеалом.
Візьмемо будь–які елементи
x2
+4ÎI, x+2ÎI.
Перевіримо чи x2
+4Mx+2.
x2
+4=x2
–4+8=(x-2) (x+2)+8.
Так як x2
+4 не ділиться на x+2 то дана множина I не буде головним ідеалом.
Відповідь:
Множина I буде ідеалом, але не головним.
№2
Знайти НСД і НСК таких многочленів:
f(x)=x4
+2x3
–2x-1,
g(x)=(x+1) (x2
–x-2)
в кільці Q[x].
Розв’язання.
Розкладемо дані многочлени на множники:
f(x)=x4
–1+2x(x2
–1)=(x2
–1) (x2
+2x+1)=(x+1)3
(x-1),
g(x)=(x+1) (x-2) (x+1)=(x+1)2
(x-2).
Очевидно, що
(f, g)=(x+1)2
,
[f, g]=(x+1)3
(x-1) (x-2).
Відповідь:
(f, g)=(x+1)2
, [f, g]=(x+1)3
(x-1) (x-2).
№3
Розкласти на незвідні в полі P множники такий многочлен:
f(x)=x4
–2x3
–27x2
–44x+7.
Розв’язання.
Розклад матиме такий вигляд:
f(x)=(x2
+bx+1) (x2
+cx+7).
f(x)=x4
+(c+b) x3
+(bc+8) x2
+(7b+c) x+7.
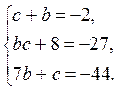
с=–2-b,
(–2-b) b=–35,
– b2
–2b=–35,
b2
+2b-35=0,
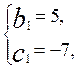 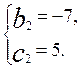
Отже, даний многочлен розкладається таким чином:
f(x)=(x2
–7x+1) (x2
+5x+7).
Відповідь:
f(x)=(x2
–7x+1) (x2
+5x+7).
3.3 Кільце многочленів від кількох змінних
3.3.1 Поняття кільця многочленів від кількох змінних
Означення
Кільцем многочленів R
[х1
, х2
,…, xn-1
, хn
] від n змінних х1
, х2
,…, xn-1
, хn
над областю цілісності R
називається кільце многочленів від змінної xn
над кільцем R
[х1
, х2
,…, xn-1
] тобто
R
[х1
, х2
,…, xn-1
, хn
] = R
[х1
, х2
,…, xn-1
] [xn
] (4)
Це означення має індуктивний характер. При п=1 воно зводиться до означення кільця многочленів від однієї змінної х1
над областю цілісності R
(природно вважати, що при п =1 R
[х1
, х2
,…, xn-1
, хn
] =R
). Якщо ж уже означено кільце R
[х1
, х2
,…, xn-1
] при п³
1, то за допомогою (4) дістаємо означення кільця R
[х1
, х2
,…, xn-1
, хn
]. Отже, для довільного натурального п означено кільце многочленів від п змінних х1
, х2
,…, xn-1
, хn
Теорема
Кільце многочленів R
[х1
, х2
,…, xn-1
, хn
] над областю цілісності R
є область цілісності.
Доведення.
Твердження правильне при п = 1. Припустимо, що воно правильне при п = т і розглянемо кільце R
[х1
, х2
,…, xm
, хm+1
]. Згідно з означенням 1, R
[х1
, х2
,…, xm
, хm+1
] є кільце многочленів над R
m
= R
[х1
, х2
,…, xm
]. За припущенням індукції, R
, є область цілісності. Отже, R
m
[xm+1
]=R
[х1
, х2
,…, xm
, хm+1
] є область цілісності. За принципом індукції, R
[х1
, х2
,…, xn-1
, хn
] є область цілісності при довільному натуральному п.
Доведено.
Зрозуміло, що коли R
– область цілісності з одиницею, то R
[х1
, х2
,…, xn-1
, хn
] – область цілісності з одиницею.
Наступна теорема встановлює будову елементів області цілісності R
[х1
, х2
,…, xn-1
, хn
].
Теорема 2.
Кожний елемент fÎR
[х1
, х2
,…, xn-1
, хn
] можна подати у вигляді скінченної суми
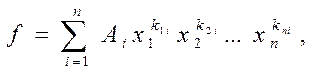 Ai
ÎR,
kij
ÎZ+
(5) Ai
ÎR,
kij
ÎZ+
(5)
Навпаки, будь-який вираз виду (5) є елементом кільця R
[х1
, х2
,…, xn-1
, хn
].
Доведення
Доведення проведемо індукцією по n. При n=1 твердження правильне. Припустимо, що воно правильне при n=m і перевіримо його правильність при n=m+1. За означенням 1, кожний елемент fÎR
[х1
, х2
,…, xm
, хm+1
] є многочлен від Хm=1
над областю цілісності R
[х1
, х2
,…, xm
], і тому його можна подати у вигляді суми
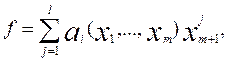 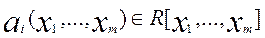 (6) (6)
За припущенням індукції, кожний многочлен aj
(x1
, …, xm
) від n змінних можна подати у вигляді скінченної суми
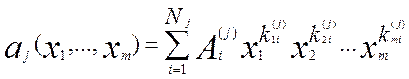 , (7) , (7)
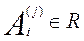 , , 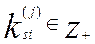
(i=1, 2, …, Nj
; s=1, 2, …, m; j=0, 1, 2, …, l).
Підставивши вираз (7) в (6) і виконавши відповідні дії (в розумінні дій у кільці R
[х1
, х2
,…, xm
, хm+1
] з урахуванням того, що воно містить R
[х1
, х2
,…, xm
] як підкільце), дістанемо скінченну суму виду
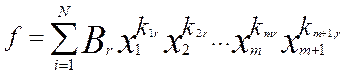 , (8) , (8)
де Br
ÎR
(r=1, …, N), бо кожне Br
є якесь з 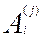 . .
Навпаки, кожна сума виду (8) є елемент кільця R
[х1
, х2
,…, xm
, хm+1
]: адже будь-який її доданок 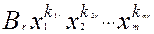 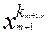 може розглядатись як многочлен від xm+1
з коефіцієнтом може розглядатись як многочлен від xm+1
з коефіцієнтом 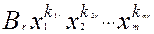 ÎR
[х1
, х2
,…, xm
] й тому й уся сума належить кільцю R
[х1
, х2
,…, xm
, хm+1
]. ÎR
[х1
, х2
,…, xm
] й тому й уся сума належить кільцю R
[х1
, х2
,…, xm
, хm+1
].
Отже, твердження теореми правильне і при n=m+1, тобто за принципом математичної індукції теорему доведено.
Доведено.
Означення
Кожний елемент кільця R
[х1
, х2
,…, xn
] називають многочленом від n змінних х1
, х2
,…, xn
над R
. і позначають f(х1
, х2
,…, xn
), g(х1
, х2
,…, xn
) і т. п.
Згідно з теоремою 2, будь-який многочлен з R
[х1
, х2
,…, xn
] можна подати у формі суми (5)
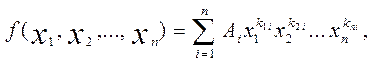 Ai
ÎR,
kij
ÎZ+
(9) Ai
ÎR,
kij
ÎZ+
(9)
Кожний доданок 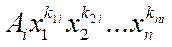 цієї суми називають членом многочлена f(х1
, х2
,…, xn
), відповідний елемент Ai
ÎR
– коефіцієнтом члена (і многочлена). Два члени, які відрізняються лише коефіцієнтами, називають подібними; іншими словами, члени подібні, якщо усі змінні входять множниками в ці члени у попарно рівних степенях, наприклад цієї суми називають членом многочлена f(х1
, х2
,…, xn
), відповідний елемент Ai
ÎR
– коефіцієнтом члена (і многочлена). Два члени, які відрізняються лише коефіцієнтами, називають подібними; іншими словами, члени подібні, якщо усі змінні входять множниками в ці члени у попарно рівних степенях, наприклад 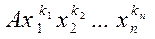 та та 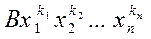 . При цьому порядок, в якому записано множники . При цьому порядок, в якому записано множники 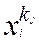 неістотний, тобто неістотний, тобто
члени 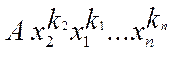 , , 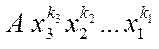 , , 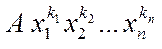 тощо вважаємо однаковими, рівними між собою. Відповідно до цього, R
[х2
, х1
,…, xn
], R
[х3
, х2
,…, x1
], R
[х1
, х2
,…, xn
] і т. п. є різними формами запису того самого кільця многочленів від змінних х1
, х2
,…, xn
над областю цілісності R
. тощо вважаємо однаковими, рівними між собою. Відповідно до цього, R
[х2
, х1
,…, xn
], R
[х3
, х2
,…, x1
], R
[х1
, х2
,…, xn
] і т. п. є різними формами запису того самого кільця многочленів від змінних х1
, х2
,…, xn
над областю цілісності R
.
Задачі
№1
Виразити через σі
такий многочлен
f (x, y)=x3
y+y3
x+2x2
+2y2
.
Розв’язання.
Основні симетричні многочлени σ1
, σ2
мають вигляд:
σ1
=x+y,
σ2
=xy.
Виразимо даний многочлен через σ1
, σ2
f (x, y)=xy(x2
+y2
)+2 (x2
+y2
)=(x2
+y2
) (xy+2)=
=((x+y)2
–2xy) (xy+2)=(σ1
–2σ2
) (σ2
+2)=
=σ1
2
σ2
+2σ1
2
–2σ2
2
–4σ2
.
Відповідь:
f (x, y)=σ1
2
σ2
+2σ1
2
–2σ2
2
–4σ2
.
№2
Довести, що для Sn
=xn
+yn
, nÎN, при n>2 виконується рекурентне співвідношення
Sk
=σ1
Sk–1
–σ2
Sk–2
.
Доведення.
Доведемо методом математичної індукції.
Перевіримо базу індукції при n=3
S3
=σ1
S2
–σ2
S1
=(x+y) (x2
+y2
) – xy (x+y)=x3
+y3
.
Припустимо, що твердження вірне для n=k.
Доведемо, що дане твердження справджується і при n=k+1
Sk+1
=σ1
Sk
–σ2
Sk–1
=(x+y) (xk
+yk
) – xy(xk–1
+yk–1
)=
=xk+1
+xyk
+xk
y+yk+1
–xk
y–xyk
=xk+1
+xk+1
.
Отже, виходячи з математичної індукції твердження доведено.
Доведено.
3.3.2 Факторіальність кільця поліномів від n змінних
Теорема. Нехай К – факторіальне кільце. Тоді кільце поліномів К[х1
,….хn
] від х1
,…., хn
над К також являється факторіальним.
Доведення.
Теорема доводиться індукцією по n. Для n=1 твердження правильне. Припустимо, що кільце поліномів К[х1
,….хn–1
] від х1
,….хn–1
, над К факторіальне. Доведемо, що факторіальним тоді буде і кільце К[х1
,…, хn
].
К[х1
,…, хn
]=К[х1
]… [.хn
]=(К[х1
,….хn–1
]) [xn
].
За індуктивним припущенням, кільце К[х1
,…, хn–1
] факторіальне. Тоді факторіальним є також його розширення (К[х1
,….хn–1
]) [xn
] за допомогою елемента xn
, трансцендентного над кільцем К[х1
,….хn–1
]. Таким чином, кільце поліномів К[х1
,….хn
] факторіальне для довільного натурального n.
Доведено.
Наслідок Кільце поліномів F[х1
,….хn
] над полем F факторіальне.
Задачі
№1
Розкласти на множники найменшого степеня з дійсними коефіцієнтами такий многочлен
f (x, y)=10x4
–27x3
y-110x2
y2
–27xy3
+10y4
.
Розв’язання.
f (x, y)=10x4
–27x3
y-110x2
y2
–27xy3
+10y4
=10 (x4
+y4
) – 27 (x2
+y2
)–110x=
=10 [(σ1
2
–2σ2
)2
–2σ2
2
]–27σ2
(σ1
2
–2σ2
)–110σ2
2
=10σ1
4
–67σ1
2
σ2
–36σ2
2
.
Розкладемо цей вираз на множники. Для цього знайдемо його корені.
σ2
′
=–2σ1
2
,
σ2
′′
=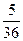 σ1
2
. σ1
2
.
Тоді наш многочлен
f=–36 (σ2
–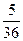 σ1
2
) (σ2
+2σ1
2
)=(–36σ2
+5σ1
2
) (σ2
+2σ1
2
). σ1
2
) (σ2
+2σ1
2
)=(–36σ2
+5σ1
2
) (σ2
+2σ1
2
).
f (x, y)=(–36xy+5 (x+y)2
) (xy+2 (x+y)2
=
=(–36xy+5x2
+10xy+5y2
) (2x2
+3xy+2y2
)=
=(5x2
–26xy+5y2
) (2x2
+3xy+2y2
).
Розглянемо кожний з цих множників, як квадратний тричлен відносно x
5x2
–26xy+5y2
x′=5y, x′′=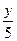 . .
2x2
+3xy+2y2
x′=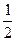 y, x′′=–2y. y, x′′=–2y.
Тоді маємо
f (x, y)=(x+2y) (2x+y) (x-5y) (5x–y).
Відповідь:
f (x, y)=(x+2y) (2x+y) (x-5y) (5x–y).
Використана література
1. Алгебра і теорія чисел, ч. 1. Завало С.Т., Костарчук В.М., Хацет Б.І. Видавниче об’єднання «Вища школа», 1974, 464 с.
2. Алгебра і теорія чисел, ч. 2. Завало С.Т., Костарчук В.М., Хацет Б.І. Видавниче об’єднання «Вища школа», 1976, 384 с.
3. Алгебра и теория чисел: Учебное пособие для педагогических институтов.–М.: Высшая школа, 1979, – 559 с., ил.
4. Збірник задач з теорії чисел. [Навчальний посібник для студентів фізико-математичного факультету] За ред. І.О. Рокіцького, Вінниця, 2001–115 с.
5. Збірник задач з алгебри. [навчальний посібник для студентів фізико-математичного факультету] За ред. І.О. Рокіцького, Вінниця, 2002–176 с.
6. Алгебра і теорія чисел: Практикум. Частина 2 /С.Т. Завало, С.С. Левіщенко, В.В. Пилаєв, І.О. Рокіцький. – К.: Вища школа Головне видавництво, 1986. – 364 с.
7. Збірник задач і вправ з теорії чисел. Є.П. Морокішко. Центр «Магістр-S», 1995 р. 158 с.
|