Городская открытая научно – практическая конференция
Тема: Решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями Автор: Научный руководитель: 2007 г.
Содержание 1. Введение
2. Решение уравнений с параметрами
3. Решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями
4. Заключение
5. Используемая литература
Введение
Актуальность
данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдачи Единого Государственного экзамена и на вступительных экзаменах в высшие учебные заведения.
Цель
данной работы рассказать о решении уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями.
Для достижения поставленной цели необходимо решить следующие задачи
:
1) дать определения понятиям уравнение с параметрами;
2) показать принцип решения данных уравнений на общих случаях;
3) показать решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями.
Для выполнения поставленной цели были использованы следующие методы
: использование литературы разного типа, работа в группах на уроках алгебры и занятиях элективного курса по математике, участие проектной группы в городской конференции по данной теме в 2006 году.
Объектом исследовательской работы
было решение уравнений с параметрами, связанных со свойствами выше представленных функций.
Структура данной работы
включает в себя теорию, практическую часть, заключение, библиографический список.
Решение уравнений с параметрами
Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение. Такие задачи предлагаются на едином государственном экзамене и на вступительных экзаменах в вузы.
Большинство пособий адресовано абитуриентам, однако начинать знакомиться с подобными задачами нужно намного раньше – параллельно с соответствующими разделами школьной программы по математике.
Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение параметрическим.
Реклама

Естественно, такой небольшой класс задач многим не позволяет усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет «общаться» с параметром как с числом, а во-вторых, - степень свободы общения ограничивается его неизвестностью. Так, деление на выражение, содержащее параметр, извлечение корня четной степени из подобных выражений требуют предварительных исследований. Как правило, результаты этих исследований влияют и на решение, и на ответ.
Основное, что нужно усвоить при первом знакомстве с параметром, - это необходимость осторожного, даже, если хотите, деликатного обращения с фиксированным, но неизвестным числом. Этому, по нашему мнению, во многом будут способствовать наши примеры.
Необходимость аккуратного обращения с параметром хорошо видна на тех примерах, где замена параметра числом делает задачу банальной. К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение, неравенство и т.д.
Обычно в уравнение буквами обозначают неизвестные.
Решить уравнение - значит:
найти множество значений неизвестных, удовлетворяющих этому уравнению. Иногда уравнения, кроме букв, обозначающих неизвестное(X, Y,Z), содержат другие буквы, называемые параметрами(a, b, c). Тогда мы имеем дело не с одним, а с бесконечным множеством уравнений.
При одних значениях параметров уравнение не имеет корней, при других – имеет только один корень, при третьих – два корня.
При решении таких уравнений надо:
1) найти множество всех доступных значений параметров;
2) перенести все члены, содержащие неизвестное, в левую часть уравнения, а все члены, не содержащие неизвестного в правую;
3) привести подобные слагаемые;
4) решать уравнение ax = b.
Возможно три случая.
1. а 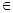 0, b – любое действительное число. Уравнение имеет единственное решение х = 0, b – любое действительное число. Уравнение имеет единственное решение х = 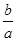 . .
2. а = 0, b = 0. Уравнение принимает вид: 0х = 0, решениями являются все х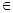 R. R.
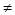 3. а = 0, b0. Уравнение 0х = b 3. а = 0, b0. Уравнение 0х = b
решений не имеет.
Сделаем одно замечание. Существенным этапом решения уравнений с параметрами является запись ответа. Особенно это относится к тем примерам, где решение как бы «ветвится» в зависимости от значений параметра. В подобных случаях составление ответа – это сбор ранее полученных результатов. И здесь очень важно не забыть отразить в ответе все этапы решения.
Реклама

В только что разобранном примере запись ответа практически повторяет решение. Тем не менее, я считаю целесообразным привести ответ.
Ответ:
х = 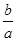 при а при а 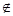 0, b – любое действительное число; 0, b – любое действительное число;
х – любое число при а = 0, b = 0;
решений нет при а = 0, b ≠ 0.
Решение уравнений с параметрами, связанных со свойствами показательной, тригонометрической и логарифмической функциями
1. Найдем значения параметра n, при которых уравнение 15·10 х
– 20 = n – n · 10х + 1
не имеет корней?
Решение
: преобразуем заданное уравнение: 15·10 х
– 20 = n – n · 10х + 1
; 15·10 х
+ n· 10х + 1
= n + 20; 10 х
·(15 + 10n) = n + 20; 10 х
= 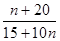 . .
Уравнение не будет иметь решений при 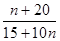 ≤ 0, поскольку 10 х
всегда положительно. ≤ 0, поскольку 10 х
всегда положительно.
Решая указанное неравенство методом интервалов, имеем: 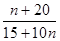 ≤ 0; (n + 20)·(15 + 10n) ≤ 0; - 20 ≤ n ≤ - 1,5. ≤ 0; (n + 20)·(15 + 10n) ≤ 0; - 20 ≤ n ≤ - 1,5.
Ответ
: 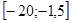 . .
2. Найдем все значения параметра а
, при которых уравнение lg2
(1 + х2
) + (3а – 2)· lg(1 + х2
) + а2
= 0 не имеет решений.
Решение
: обозначим lg(1 + х2
) = z, z > 0, тогда исходное уравнение примет вид: z2
+ (3а – 2) · z + а2
= 0. Это уравнение – квадратное с дискриминантом, равным (3а – 2)2
– 4а2
= 5а2
– 12а + 4. При дискриминанте меньше 0, то есть при 5а2
– 12а + 4 < 0 выполняется при 0,4 < а <2.
Ответ: (0,4; 2).
3. Найдем наибольшее целое значение параметра а
, при котором уравнение cos2x + asinx = 2a
– 7 имеет решение.
Решение
: преобразуем заданное уравнение:
cos2x + a
sinx = 2a
– 7; 1 – 2sin2
х – asinx = 2a
– 7; sin2
х - 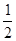 a
sinx + a – 4 = 0; a
sinx + a – 4 = 0;
(sinх – 2) · 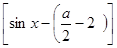 = 0. = 0.
Решение уравнения (sinх – 2) ·  = 0 дает: = 0 дает:
(sinх – 2) = 0; х принадлежит пустому множеству.
sinх - 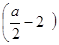 = 0; х = (-1)n
arcsin = 0; х = (-1)n
arcsin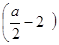 + πn, n + πn, n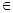 Z при Z при 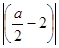 ≤ 1. Неравенство ≤ 1. Неравенство 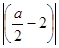 ≤ 1 имеет решение 2 ≤ а
≤ 6, откуда следует, что наибольшее целое значение параметра а равно 6. ≤ 1 имеет решение 2 ≤ а
≤ 6, откуда следует, что наибольшее целое значение параметра а равно 6.
Ответ
: 6.
4. Указать наибольшее целое значение параметра а
, при котором корни уравнения 4х2
- 2х + а
= 0 принадлежит интервалу (- 1; 1).
Решение
: корни заданного уравнения равны: х1
=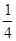 (1+ (1+ 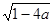 ) )
х2
=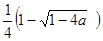 , при этом а
≤ , при этом а
≤ 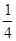 . .
По условию -1 < 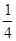 (1+ (1+ 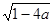 ) < 1 ) < 1 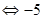 < < 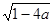 < 3, < 3,
- 1 < 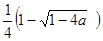 < 1 < 1 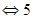 > > 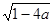 > - 3. > - 3.
Решением, удовлетворяющим указанным двойным неравенствам, будет решение двойного неравенства: - 3 < 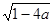 < 3. < 3.
Неравенство - 3 < 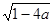 выполняется при всех а ≤ выполняется при всех а ≤ 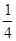 , неравенство , неравенство 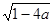 < 3 – при - 2 < а
≤ < 3 – при - 2 < а
≤ 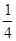 . Таким образом, допустимые значения параметра а
лежат в интервале (-2; . Таким образом, допустимые значения параметра а
лежат в интервале (-2; 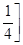 . .
Наибольшее целое значение параметра а из этого интервала, которое одновременно принадлежит и интервалу (-1; 1), равно 0.
Ответ
: 0.
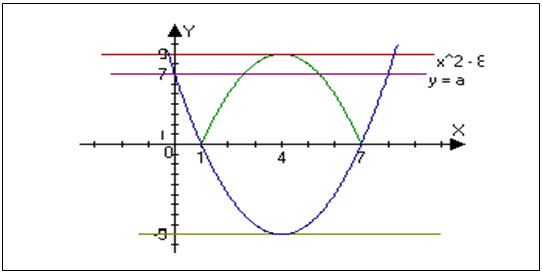
5. При каких значениях параметра а
число корней уравнения
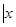 2
- 2
-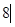 х х 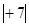 = 0 равно а? = 0 равно а?
Решение
: построим эскиз графика функции, у = 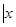 2
- 2
-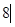 х х 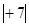 при этом учтем, что функция у – четная и ее график – симметричен относительно оси ординат, в силу чего можно ограничиться построением только его правой части ( х ≥ 0). Также учтем, что трехчлен х2
- 8х + 7 имеет корни х = 1 и х = 7, при х = 0 у = 7, а при х = 4 – минимум, равный – 9. На рисунке: пунктирными прямыми изображена парабола при этом учтем, что функция у – четная и ее график – симметричен относительно оси ординат, в силу чего можно ограничиться построением только его правой части ( х ≥ 0). Также учтем, что трехчлен х2
- 8х + 7 имеет корни х = 1 и х = 7, при х = 0 у = 7, а при х = 4 – минимум, равный – 9. На рисунке: пунктирными прямыми изображена парабола
у = х2
- 8х + 7 с минимумом умин
равным - 9 при х мин
= 4, и корнями х1
= 1 и х2
= 7;
сплошными линиями изображена часть параболы у = 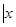 2
– 8х + 2
– 8х + 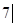 (1 < х < 7), полученная зеркальным отражением относительно оси 0х части параболы (1 < х < 7), полученная зеркальным отражением относительно оси 0х части параболы
х2
- 8х + 7 при 1 < х < 7.
(Эскиз левой части графика функции при х < 0 можно получить, отразив эскиз правой части графика симметрично относительно оси 0у).
Проводя горизонтали у = а
, а
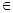 N, получаем kточек ее пересечение с линиями эскиза графика. Имеем: N, получаем kточек ее пересечение с линиями эскиза графика. Имеем:
| а |
0 |
[1; 6] |
7 |
8 |
9 |
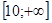 |
| к |
4 |
8 |
7 |
6 |
4 |
2 |
Таким образом, а
= k при а
= 7.
Ответ
: 7.
6. Указать значение параметра а
, при котором уравнение
х4
+ (1 – 2а)х2
+ а2
– 4 = 0 имеет три различных корня.
Решение
: всякое биквадратное уравнение в общем случае имеет две пары корней, причем корни одной пары различаются только знаком. Три корня возможны в случае, если уравнение имеет одну пару в виде нуля.
Корни заданного уравнения равны:
х = 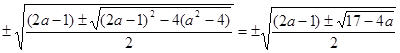
Одна из пар корней будет равна 0, если (2а-1) = 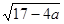 . Решая это уравнение при условии 2а-1 > 0 . Решая это уравнение при условии 2а-1 > 0 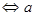 > > 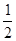 , имеем: (2а – 1) = , имеем: (2а – 1) = 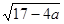 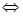 (2а – 1)2
= 17 – 4а (2а – 1)2
= 17 – 4а 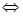
4а2
– 4а +1 = 17 – 4а 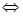 а = 2. а = 2.
Ответ
: 2.
7. Указать целое значение параметра p
, при котором уравнение
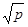 cosx – 2sinx = cosx – 2sinx = 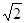 + + 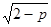 имеет решение. имеет решение.
Решение
: р
≥ 0; 2 – р
≥ 0 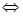 р
≤ 2; объединяя допустимые значения параметра р
, имеем: р
≤ 2; объединяя допустимые значения параметра р
, имеем:
0 ≤ р
≤ 2.
При р
= 0 исходное уравнение принимает вид – 2sinх = 2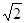 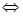 х принадлежит пустому множеству ( в силу ограниченности синуса). х принадлежит пустому множеству ( в силу ограниченности синуса).
При р
= 1 исходное уравнение принимает вид:
cosx-2sinx = 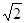 +1. +1.
Максимальное значение разности (cosx-2sinx) составляет
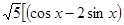 = (- sinx – 2cosx) = 0 = (- sinx – 2cosx) = 0 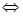 tgx = -2, при этом sinx= tgx = -2, при этом sinx=
sin (arctg(-2)) = 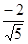 , cosx – 2sinx = , cosx – 2sinx = 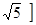 , что меньше , что меньше 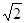 +1. +1.
Следовательно, при р
= 1 уравнение решений не имеет.
При р
= 2 исходное уравнение принимает вид
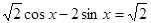 . .
Максимальное значение разности 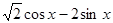 составляет составляет 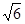 при х = arctg(- при х = arctg(-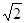 ) (при этом sinx = ) (при этом sinx = 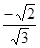 , cosx = , cosx = 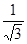 ). Поскольку ). Поскольку 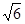 > > 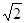 +1, то уравнение +1, то уравнение 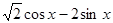 = = 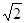 будет иметь решение. будет иметь решение.
Ответ
: 2.
8. Определить число натуральных n, при которых уравнение 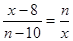 не имеет решения. не имеет решения.
Решение
: х ≠ 0, n ≠ 10.
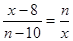 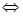 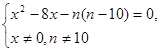
Уравнение х2
– 8х – n(n – 10) = 0 не имеет решения, если его дискриминант меньше 0, т.е. 16 + n(n-10) < 0 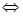 n2
-10n +16 < 0 n2
-10n +16 < 0 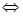 (n-2) (n-8) <0 (n-2) (n-8) <0 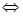 2 < n < 8. 2 < n < 8.
В найденном интервале 5 натуральных чисел: 3, 4, 5, 6 и 7. Учитывая условие n ≠ 10, находим, что общее число натуральных n, при которых уравнение не имеет решений, равно 6.
Ответ
: 6.
9. Найти наименьшее целое значение параметра а, при котором уравнение 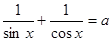 (0 < х < (0 < х < 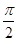 ) имеет решение. ) имеет решение.
Решение
: по условию 1 > sinx> 0 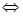 1 < 1 < 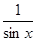 < + < + 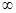 , ,
1 > cosx> 0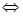 1 < 1 < 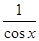 < + < + 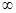 , ,
Следовательно, 2 < а < + 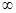 . .
Возводя обе части заданного уравнения в квадрат, имеем:
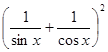 = а2 = а2 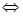
 = а2 = а2
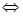
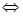 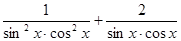 = а2
. = а2
.
Введем переменную z = 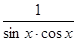 . Тогда исходное уравнение примет вид: . Тогда исходное уравнение примет вид:
z2
+ 2z – а2
= 0. Оно имеет решение при любом а,
поскольку его дискриминант
D = 1 + а2
положителен при любом а
.
Учитывая, что 2 < а
< + 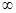 , заключаем, что наименьшее целое значение параметра а
, при котором заданное уравнение имеет решение равно 3. , заключаем, что наименьшее целое значение параметра а
, при котором заданное уравнение имеет решение равно 3.
Ответ
: 3.
Заключение
Во время создания данного проекта мы усовершенствовали свои старые знания по теме «Уравнения с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями » и в какой-то мере получили новые.
По завершению работы мы пришли к выводу, что эта тема должна изучаться не только на элективных курсах и дополнительных занятиях, но и в школьной программе, так как она формирует логическое мышление и математическую культуру у школьников. Учащимся (студентам) знания по этой теме помогут сдать Единый Государственный Экзамен и вступительные экзамены в ВУЗы.
Используемая литература.
1. П.И.Горнштейн, В.Б.Полонский, М.С.Якир «Задачи с параметрами», 2002г.
2. Н.Ю.Глаголева «Задачи по математике для поступающих в вузы», 1994г.
3. В.В.Локоть «Задачи с параметрами», 2003г.
4. В.В.Ткачук «Математика – абитуриенту», 1994г.
5. Г.А.Ястребинецкий «Уравнения и неравенства, содержащие параметры», 1972г.
6. А.Г.Мордкович «Алгебра и начала анализа», 1987г.
7. В.С.Крамов «Повторяем и систематизируем школьный курс алгебры и начала анализа», 1994г.
8. «Математика. Решение задач повышенной сложности», 2004г.
9. М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, Р.Г. Газарян «Алгебра и начала анализа», 2000г.
10. А.П. Карп «Даю уроки математики…», 1992 г.
11. В.В. Ткачук «Математика – абитуриенту», 1996 г.
|