Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса
1. Постановка задачи
При решении многих задач физики и других прикладных наук возникает необходимость вместо функции 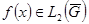 , рассматривать функцию , рассматривать функцию 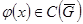 , представляющую функцию , представляющую функцию 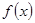 как можно «хорошо». как можно «хорошо».
Например: 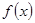 может быть, в частности, и непрерывной функцией на может быть, в частности, и непрерывной функцией на 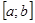 , а , а 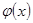 соответствующая соответствующая 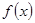 - алгебраическим или тригонометрическим многочленом, который «достаточно хорошо» приближает функцию - алгебраическим или тригонометрическим многочленом, который «достаточно хорошо» приближает функцию 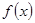 . .
Например: всякую 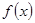 функцию из функцию из 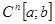 можно представить приближённо соответствующим многочленом степени можно представить приближённо соответствующим многочленом степени 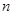 с помощью формулы Тейлора: с помощью формулы Тейлора:
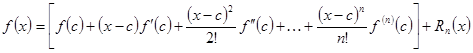 (1) (1)
т.е.
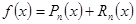 ; ; 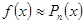 (2) (2)
где 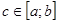 , , 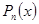 - многочлен степени - многочлен степени 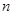 , приближающий функцию , приближающий функцию 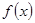 , , 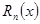 - остаточный член. Ясно, что - остаточный член. Ясно, что
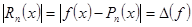 (3) (3)
т.е. 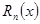 - характеризует абсолютную погрешность приближения функции - характеризует абсолютную погрешность приближения функции 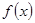 многочленом многочленом 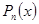 в точке в точке 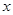 . .
Известно также, что 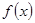 можно приблизить с помощью тригонометрического многочлена – отрезка ряда Фурье. можно приблизить с помощью тригонометрического многочлена – отрезка ряда Фурье.
В утверждение, что функция 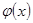 хорошо приближает функцию хорошо приближает функцию 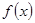 на компакте на компакте 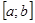 , может быть вложен разный смысл. Например: , может быть вложен разный смысл. Например:
а) можно потребовать, чтобы приближающая функция 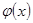 совпадала с совпадала с 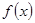 в в 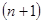 точках промежутка точках промежутка 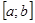 , т.е. выполнялись условия , т.е. выполнялись условия 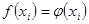 , для , для 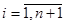 . .
Если 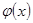 - многочлен степени - многочлен степени 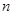 , то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена (частным примером является многочлен Лагранжа, т.е. , то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена (частным примером является многочлен Лагранжа, т.е. 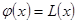 ); );
б) функцию 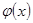 можно выбрать так, чтобы норма можно выбрать так, чтобы норма 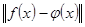 - отклонения невязки – достигала минимального значения, причём норма может быть определена по-разному, и разным нормам соответствуют различные степени приближения. - отклонения невязки – достигала минимального значения, причём норма может быть определена по-разному, и разным нормам соответствуют различные степени приближения.
В функциональном пространстве Гильберта 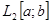 , норме невязки имеет вид (интегральная норма Гаусса): , норме невязки имеет вид (интегральная норма Гаусса):
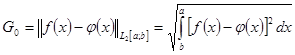 (4) (4)
часто, в качестве нормы рассматривают Чебышевскую норму (Т – первая буква фамилии Чебышева на немецком языке):
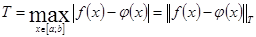 (5) (5)
При использовании нормы (5) говорят о равномерном приближении функции 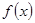 , функцией , функцией 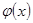 . .
Подробная теория Т-приближений была развита в работах немецкого математика Л. Коллатца.
На практике, для оценки характера приближения, часто применяют метод наименьших квадратов, при котором невязка вычисляется по дискретной норме Гаусса:
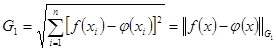 (6) (6)
Ясно, что метод наименьших квадратов (6) – является дискретным аналогом функции Гаусса (4).
Принципиальную возможность приближения любой непрерывной функции 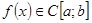 многочленом даёт теорема Вейерштрасса: Если многочленом даёт теорема Вейерштрасса: Если 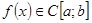 , тогда , тогда 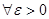 , , 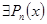 - многочлен, что - многочлен, что 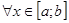 имеет место неравенство: имеет место неравенство:
Реклама

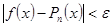 (7) (7)
2. Метод наименьших квадратов в случае приближения функции 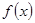
Мы ранее рассматривали задачу аппроксимации результатов неточного эксперимента линейной функцией 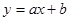 . Сейчас рассмотрим общий случай, когда функция . Сейчас рассмотрим общий случай, когда функция 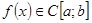 приближается некоторой системой линейно независимых функций приближается некоторой системой линейно независимых функций 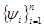 . .
Как известно, для линейной независимости системы функций 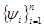 необходимо и достаточно, чтобы определитель Грама этой системы был отличен от нуля, т.е. необходимо и достаточно, чтобы определитель Грама этой системы был отличен от нуля, т.е.
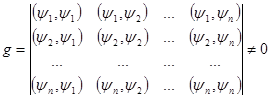 (8) (8)
где 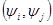 означают скалярные произведения. Тогда для приближения (аппроксимации) функции означают скалярные произведения. Тогда для приближения (аппроксимации) функции 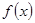 применяется линейная комбинация системы базисных функций, т.е. применяется линейная комбинация системы базисных функций, т.е.
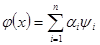 (9) (9)
В приближающей функции 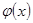 , неизвестными являются коэффициенты разложения , неизвестными являются коэффициенты разложения 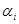 , которые подбираются из условия минимума невязки, подсчитываемой по соответствующей норме. Вообще говоря, , которые подбираются из условия минимума невязки, подсчитываемой по соответствующей норме. Вообще говоря, 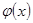 является элементом линейной оболочки, натянутой на систему базисных функций является элементом линейной оболочки, натянутой на систему базисных функций 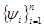 . .
2.1 Квадратичное приближение таблично заданной функции 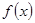 по дискретной норме Гаусса по дискретной норме Гаусса
Рассмотрим задачу приближения функции 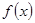 в случае использования невязки в форме (6). Т.е. используем дискретную норму Гаусса: в случае использования невязки в форме (6). Т.е. используем дискретную норму Гаусса:
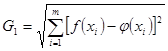 (10) (10)
где неизвестная функция 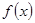 аппроксимируется функцией аппроксимируется функцией 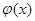 из (9). Для из (9). Для 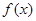 известны лишь значения в известны лишь значения в 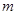 различных точках различных точках 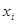 , т.е. , т.е. 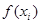 , где , где 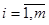 . Таким образом, для определения . Таким образом, для определения 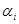 имеем задачу: найти точку минимума имеем задачу: найти точку минимума 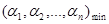 - невязки функции Гаусса - невязки функции Гаусса 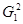 - для таблично заданной функции - для таблично заданной функции 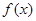 , если , если
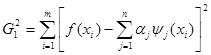 , (где , (где 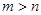 ). (11) ). (11)
Очевидно, что условия минимума дискретной функции невязки Гаусса 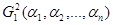 - имеют вид: - имеют вид:
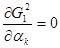 , , 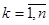 (12) (12)
Эти условия для (11) преобразуются к виду:
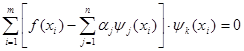 , , 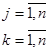 (13) (13)
Раскрывая систему (13) получаем систему уравнений для определения коэффициентов разложения 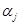 в виде: в виде:
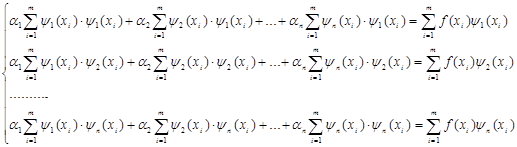 (14) (14)
Нетрудно увидеть, что вводя скалярные произведения в соответствующем функциональном пространстве в виде:
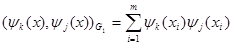 (15) (15)
систему (14) можно переписать в нормальном виде Гаусса:
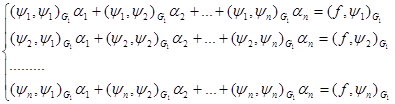 (16) (16)
Ясно, что эта система имеет единственное решение, т.к. определитель системы (16) совпадает с определителем
Грама для базисных функций 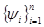 - которая отлична от нуля вследствие линейной независимости базисных функций. - которая отлична от нуля вследствие линейной независимости базисных функций.
Найдя 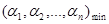 из системы (16) и подставляя в (9) мы получаем функцию: из системы (16) и подставляя в (9) мы получаем функцию:
 (17) (17)
которая является приближением к функции 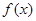 в смысле минимума квадратичного отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно: в смысле минимума квадратичного отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно:
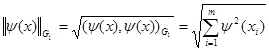 (18) (18)
а дискретная норма Гаусса невязки имеет вид:
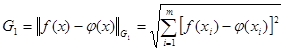 (19) (19)
2.2 Интегральное приближение функции 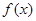 заданной аналитически заданной аналитически
В предыдущем параграфе мы рассматривали приближение функции 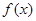 методом наименьших квадратов, предполагая, что значения функции методом наименьших квадратов, предполагая, что значения функции 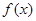 заданы таблично, поэтому мы пользовались дискретной нормой Гаусса заданы таблично, поэтому мы пользовались дискретной нормой Гаусса 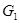 . .
Реклама

Рассмотрим теперь случай, когда аналитически заданную, на интервале 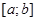 , функцию , функцию 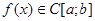 - надо аппроксимировать обобщённым многочленом: - надо аппроксимировать обобщённым многочленом:
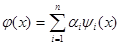 (20) (20)
так, чтобы минимизировалась интегральная норма невязки Гаусса 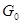 : :
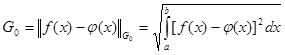 (21) (21)
иначе говоря, нам нужно минимизировать интеграл
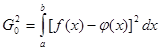 (22) (22)
Для решения этой задачи подставим (20) в (22), тогда функционал (22) превратится в функцию многих переменных, т.е. 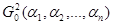 . Условия же минимума функции многих переменных имеют вид: . Условия же минимума функции многих переменных имеют вид:
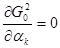 , , 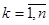 (23) (23)
Эти условия приобретают вид:
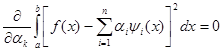 (24) (24)
т.е.
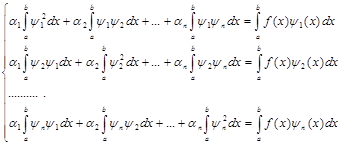 (25) (25)
Определитель этой системы представляет собой определитель Грама для функций 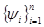 , в , в 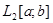 , поэтому система (25) имеет единственное решение , поэтому система (25) имеет единственное решение 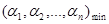 . Подставляя эти значения в разложение (20) имеем приближение для . Подставляя эти значения в разложение (20) имеем приближение для 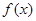 . Характер приближения оценивается соответствующей нормой невязки . Характер приближения оценивается соответствующей нормой невязки 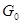 . .
Задача аппроксимации функции заданной аналитически часто применяется для вычисления интегралов.
2.3 Числовые примеры на применение метода наименьших квадратов Гаусса для приближения функций заданных таблично или аналитически
а) Рассмотрим пример в случае табличного задания функции 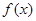 : :
Пример 1:
пусть функция 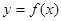 задана таблично: задана таблично:
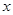 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
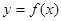 |
0.31 |
0.82 |
1.29 |
1.85 |
2.51 |
3.02 |
с помощью метода наименьших квадратов аппроксимировать эту функцию в классе линейных функций. Т.е. допускаем, что 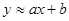 . Для нахождения коэффициентов . Для нахождения коэффициентов 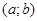 , составляем невязку по дискретной норме Гаусса: , составляем невязку по дискретной норме Гаусса:
 (26) (26)
Необходимые условия минимума для 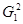 имеют вид: имеют вид:
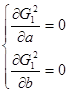 (27) (27)
Из (27) – получаем нормальные уравнения Гаусса:
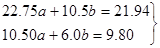 (28) (28)
Решение имеет вид:
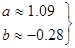 (29) (29)
т.е.
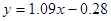 (30) (30)
б) Теперь, рассмотрим пример в случае приближения сложных аналитически заданных 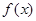 функций, боллее простыми функций, боллее простыми 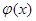 функциями. функциями.
Пример 2:
Функцию 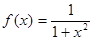 , заданную на интервале , заданную на интервале 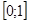 аппроксимировать линейной функцией аппроксимировать линейной функцией 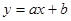 , определив параметры , определив параметры 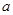 и и 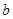 по методу Гаусса (используем интегральную норму невязки Гаусса). по методу Гаусса (используем интегральную норму невязки Гаусса).
Решение:
интегральная норма невязки для данной функции имеет вид:
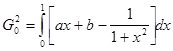 (31) (31)
Необходимые условия минимума для 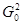 - имеют вид: - имеют вид:
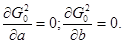 (32) (32)
т.е.
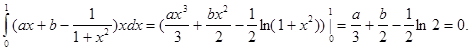 (33) (33)
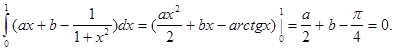 (34) (34)
Из уравнений (33) и (34) находим 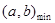
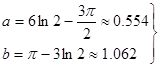 (35) (35)
аппроксимирующий многочлен имеет вид:
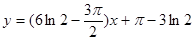 (36) (36)
или
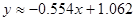 (37) (37)
Для более глубокого изучения теории приближения, необходимо знание численных методов вычисления интегралов и методов решения систем уравнения, поэтому на следующей лекции мы временно прервем изложение теории аппроксимации и перейдем на подготовительную работу.
Литература
1). К. Ректорис. Вариационные методы в математической физике и механике. Мир, М.,1995
2). С.Г. Михлин. Численная реализация вариационных методов, М., Наука, 1996
3). Л.А. Кальницкий, Д.А. Добротин, В.Ф. Жевердеев. Специальный курс высшей математики для втузов. М., ”Высшая математика”, 1996
4). Т. Шуп. Решение инженерных задач на ЭВМ. Мир, М., 1982
5). Л. Коллатц. Функциональный анализ и вычислительная математика. Мир, М., 1999
6). Р. Варга. Функциональный анализ и теория аппроксимации в численном анализе. Мир, М., 1994
7). Л. Коллатц, Ю. Альбрехт. Задачи по прикладной математике. Мир, М.,1998.
|