Міністерство освіти і науки України
Вінницький національний технічний університет
Інститут АЕКСУ
Кафедра АІВТ
Контрольна робота
з дисципліни:
“Моделювання на ЕОМ”
Дослідження однокрокових методів розв’язання звичайних диференційних рівнянь
Виконав: ст. гр. 1АМ-04_____ Балко О.О.
Перевірив: доцент каф.АІВТ_____ Кабачій В.В.
2007
Вступ
1 Короткі теоретичні відомості
2 Алгоритми методів
2.1Блок-схеми алгоритмів розв'язку даного диференційного рівняння
3 Вхідні та вихідні дані1
4. Аналіз результатів моделювання
4.1 Розв’язок диференціального рівняння в Mathcad
5. Інструкція користувачу
Висновки
Література
Додаток А. Лістинг програми
Вступ
На даний момент велика роль в розвитку сучасного світу відводиться підвищенню технічного рівня обчислювальної техніки, пристроїв і засобів автоматизації. Це передбачає розвиток виробництва і широке використання промислових роботів, систем автоматичного управління з використанням мікропроцесорів і мікро-ЕОМ, створення гнучких автоматизованих виробництв. Розв'язок цих задач потребує широкого упровадження в інженерну практику методів обчислювальної математики.
Обчислювальна математика заснована на чисельних методах, придатних до застосування при розрахунках на ЕОМ. Сучасні ЕОМ дозволили дослідникам значно підвищити ефективність математичного моделювання складних задач науки і техніки. Нині методи дослідження проникають практично в усі сфери людської діяльності, а математичні моделі стають засобами пізнання.
Значення математичних моделей неперервно зростає у зв'язку з тенденціями до оптимізації технічних пристроїв і технологічних схем планування експерименту. Реалізація моделей на ЕОМ здійснюється за допомогою різноманітних методів обчислювальної математики, яка неперервно удосконалюється.
В даній роботі розглянуті однокрокові методи розв’язання звичайних диференційних рівнянь(на прикладі диференційного рівняння першого порядку), а саме прямий та зворотній методи Ейлера, та метод Рунге-Кутта.
Розробленна програма дозволяє розв’язати вказане диференційне рівняння методами Ейлера (прямим та зворотним) та Рунге-Кутта, порівняти їх результати та визначити похибки
1. Короткі теоретичні відомості
Найбільш простим однокроковим методом, який потребує мінімальних затрат обчислювальних ресурсів, але дає змогу обчислювати результат із порівняно низькою точністю, є метод Ейлера.
Реклама

В цьому методі для оцінки наступної точки на кривій 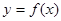 використовується лише один лінійний член в формулі Тейлора, використовується лише один лінійний член в формулі Тейлора,
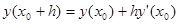 (1) (1)
де 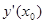 визначається з початкового рівняння. визначається з початкового рівняння.
Цей процес можна розповсюдити на наступні кроки:
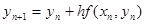 (2) (2)
Метод Ейлера є методом першого порядку 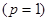
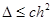 (3) (3)
де 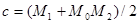 , , 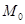 , , 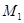 , , 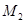 - визначається як - визначається як
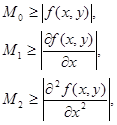 (4) (4)
для всіх 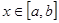 і і  . .
Метод Ейлера, крім значної похибки зрізання часто буває нестійким (малі локальні похибки призводять до значного збільшення глобальної).
Цей метод можна вдосконалити різними способами.
Найбільш відомі два з них: виправлений метод Ейлера і модифікований метод Ейлера (в літературі зустрічаються інші назви цих методів, наприклад, модифікований метод Ейлера й удосконалений метод ламаних).
Ітераційні формули для цих методів мають вигляд, відповідно:
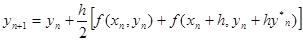 (5) (5)
І
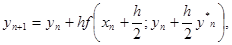 (6) (6)
Де
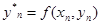 (7) (7)
Це методи другого порядку, їх похибка має третій ступінь, що досягається покращенням апроксимації похідної. Ідея полягає у спробі зберегти або оцінити член другого порядку у формулі Тейлора. Однак збільшення точності вимагає додаткових витрат машинного часу на обчислення 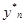 . Ще більш висока точність може бути досягнута при обчисленні вищих похідних і збереженні більшої кількості членів ряду Тейлора. Такими методами є методи Рунге-Кутта. . Ще більш висока точність може бути досягнута при обчисленні вищих похідних і збереженні більшої кількості членів ряду Тейлора. Такими методами є методи Рунге-Кутта.
Принцип на якому побудований модифікований метод Ейлера, можна пояснити, користуючись рядом Тейлора і зберігаючи в ньому член з 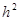 . Апроксимація другої похідної . Апроксимація другої похідної 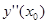 здійснюється кінцевою різницею здійснюється кінцевою різницею
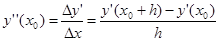 (8) (8)
Аналогічно обчисленню другої похідної в кінцево-різницевому вигляді можна обчислити більш високі похідні: значення n-ї за значеннями попередньої (n-1)-ї.
Метод Рунге-Кутта дає набір формул для обчислення координат внутрішніх точок, які потрібні для реалізації цієї ідеї. Оскільки існує ряд способів знаходження цих точок, то метод Рунге-Кутта об’єднує цілий клас методів для розв’язання диференціальних рівнянь першого порядку.
Найбільш розповсюджений класичний метод четвертого порядку точності:
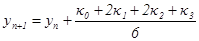 (9) (9)
Де
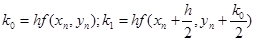 (10) (10)
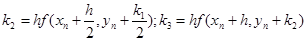 (11) (11)
Метод Ейлера і його модифікації ще називають методами Рунге-Кутта першого і другого порядку. Метод Рунге-Кутта має значно більш високу точність, що дозволяє збільшити крок розв’язання. Його максималу величину визначає допустима похибка. Такий вибір часто здійснюється автоматично і включається як складова частина, вбудована в алгоритм, побудований за методом Рунге-Кутта.
Раніше було відзначено, що помилка зрізання при використанні методу Рунге-Кутта n-го порядку 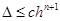 . Обчислення верхніх границь для коефіцієнта с являє собою складну задачу, пов’язану з необхідністю оцінки ряду додаткових параметрів. Існує декілька способів для оперативного обчислення с. Найбільшого поширення набув екстраполяційний метод Річардсона (ще його називають методом Рунге), коли послідовно знаходять . Обчислення верхніх границь для коефіцієнта с являє собою складну задачу, пов’язану з необхідністю оцінки ряду додаткових параметрів. Існує декілька способів для оперативного обчислення с. Найбільшого поширення набув екстраполяційний метод Річардсона (ще його називають методом Рунге), коли послідовно знаходять 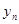 з кроком h і з кроком з кроком h і з кроком 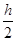 , а після цього прирівнюють отримані величини та визначають с з рівняння: , а після цього прирівнюють отримані величини та визначають с з рівняння:
Реклама

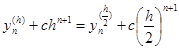 (12) (12)
що відповідає точному значенню 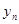 . .
Отримаємо оціночне співвідношення:
 (13) (13)
2. Алгоритми методів
В курсовій роботі розроблена програма, що розв’язує задане диференційне рівняння першого порядку трьома методами:
Ейлера : - прямим
- ЗворотнімтаРунге-Кутта
Також, програма рахує похибку на кроці та загальну похибку методу.
В основі алгоритму лежить використання однокрокових методів, в основі яких лежить знаходження наступної точки на кривій лише за значенням попередньої. Основу методу складає розкладання функції в ряд Тейлора.
Програма використовує основні функції Borland C++ 3.1, а саме:
· Цикли: while ()
for()
· Оператори безумовного переходу: If ()
else
switch()
В основі програми лежить загальний алгоритм розв’язку диференційних рівнянь однокроковими методами.
Алгоритм:
1.за початковим значенням x,y знаходимо наступну точку кривої y=f(x) при кроці h=0.1;
2.знаходимо нові значення x,y;
3.перевряємо чи х належить проміжку, на якому шукаються розв’язки: якщо х належить цьому проміжку, то алгоритм повторюється з пункту 1, де замість початкових значень x,y; використовуються нові(обчислені в пункті 2); якщо ні, то алгоритм припиняє свою роботу ;
4.аналогічно шукаються розв’язки цього ж рівняння , але при кроці h=0.05;
5.Знаходження похибки зводиться до:
· знаходження C за формулою
с=(y1-y2))/(St(h1,p+1)-St(h2,p+1))
де y1,y2-значення в одній тій самій точці розв’язку,
але обчисленні з різним кроком;
St – функція піднесення до степеня, де р+1 степінь, а h1(h2) числа, що підносяться до степеня.
· знаходження глобальної похибки, шляхом додаванняпохибок знайдених на кожному кроці обчислень;
Для данного завдання, формули знаходження наступних значень за попердніми мають вигляд:
· прямий метод Ейлера:
yn:=yn+h*(yn+0.7*xn+1.2);
· зворотній метод Ейлера:
yn:=yn+h*(0.7*xn+1.2)/(1-h);
· метод Рунге-Кутта
yn=yn+((k0+2*k1+2*k2+k3)/6);
2.1
Блок-схеми алгоритмів розв'язку даного диференційного рівняння
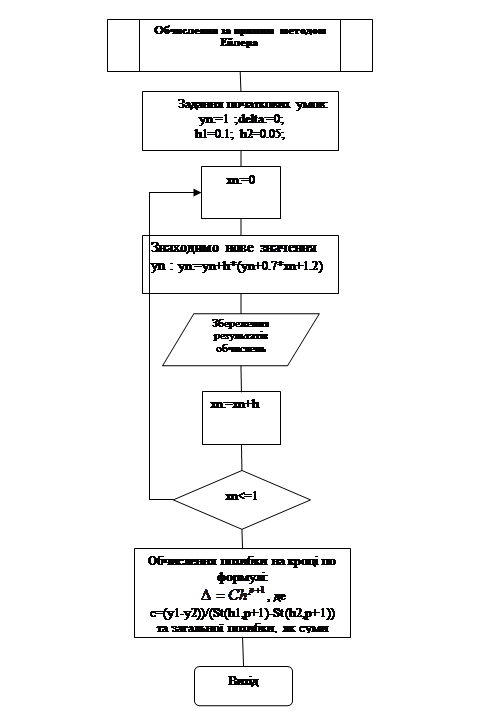
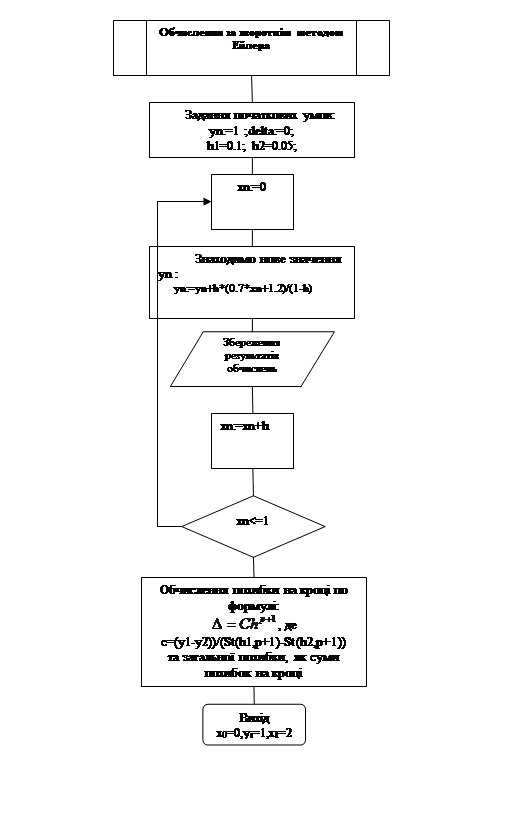

k0
=h
×f(x0
,yi
); k1
=h
×f(x0
+h/2;yi
+k0
/2);
k2
=h
×f(x0
+h/2;yi
+k1
/2);k3
=h
×f(x0
+h;yi
+k2
)
|
|
 | yi+1
=(yi
+k0
+2k1
+2k2
+k3)/6
|
|
  
   | Розрахунок локальної похибки |
|

 
3
Вхідні та вихідні дані
Вхідними даними програми є: крок обчислення і задане диференціальне рівняння.
Вихідними даними програми є: графіки, таблиця з рішеннями диференціального рівняння і похибки обчислень.
4. Аналіз результатів моделювання
Розроблена програма дозволяє розв'язувати дане диференційне рівняння трьома методами. З результатів обчислень ми можемо перевірити функціональність програми і точність кожного з методів.
Прямий метод Ейлера:
| Крок 0.1 |
Крок 0.05 |
Похибка |
| 1.000000 |
1.000000 |
0.000000 |
| 1.220000 |
1.227250 |
0.009667 |
| 1.469000 |
1.484968 |
0.030958 |
| 1.749900 |
1.776278 |
0.066128 |
| 2.065890 |
2.104621 |
0.117769 |
| 2.420479 |
2.473795 |
0.188856 |
| 2.817527 |
2.887984 |
0.282799 |
| 3.261280 |
3.351802 |
0.403495 |
| 3.756408 |
3.870337 |
0.555401 |
| 4.308049 |
4.449197 |
0.743598 |
Даний метод не є точним на що вказує глобальна похибка 0.743598.
Зворотній метод Ейлера :
| Крок 0.1 |
Крок 0.05 |
Похибка |
| 1.000000 |
1.000000 |
0.000000 |
| 1.244444 |
1.239515 |
0.006572 |
| 1.523827 |
1.512468 |
0.021717 |
| 1.842030 |
1.822472 |
0.047795 |
| 2.203367 |
2.173528 |
0.087580 |
| 2.612630 |
2.570073 |
0.144322 |
| 3.075144 |
3.017020 |
0.221821 |
| 3.596827 |
3.519814 |
0.324504 |
| 4.184252 |
4.084490 |
0.457521 |
| 4.844725 |
4.717731 |
0.626846 |
Даний метод є більш точним за прямий метод Ейлера так як його глобальна похибка складає 626846.
Метод Рунге-Кутта
| Крок 0.1 |
Крок 0.05 |
Похибка |
| 1.000000 |
1.000000 |
0.000000 |
| 1.229469 |
1.229644 |
0.000026 |
| 1.489718 |
1.489644 |
0.000103 |
| 1.783814 |
1.783663 |
0.000259 |
| 2.115130 |
2.114874 |
0.000524 |
| 2.487374 |
2.486981 |
0.000930 |
| 2.904625 |
2.904060 |
0.001513 |
| 3.371367 |
3.370593 |
0.002312 |
| 3.892533 |
3.891508 |
0.003370 |
| 4.473544 |
4.472224 |
0.004732 |
Даний метод є найточнішим серед прямого і зворотного методу Ейлера, його глобальна похибка дорівнює 0.004732.
Звідси можна зробити висновок; найбільш простим однокроковим методом, потребуючим мінімальних затрат розрахункових ресурсів, і який є дуже точним по відношенню до метода Ейлера є метод Рунге-Кутта. Метод Ейлера, крім значної похибки усічки, часто буває нестійким (малі локальні помилки приводять до значного збільшення глобальної).
4.1. Розв’язок диференціального рівняння в Mathcad
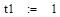
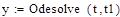
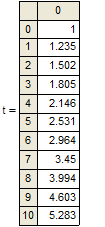
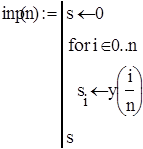
Звіримо результати обчислень. Візьмемо найточніший метод Рунге-Кутта та результат отриманий в Mathcad відповідно: 4.472 та 4.603 похибка 0.131
Тобто можна зробити висновок що результати обчислень програми і обчислення Mathcad майже співпадають.
5. Інструкція користувачу
Для завантаження необхідно переписати з дискети файл kursova.exe і запустити його, для роботи програми потрібен графічний драйвер egavga.bgi
Після завантаження слід натиснути клавішу Enter потрібну кількість разів щоб обрати потрібний метод
Після натиснення клавіші Esc відбудеться вихід з програми.
Висновки
В результаті виконання даної курсової роботи ми наглядно оцінили кожний з методів розв'язку диференційного рівняння і прийшли до висновку, що найточнішим методом з найменшою глобальною похибкою є метод Рунге-Кутта , а прямий метод Ейлера і зворотній метод Ейлера, є не досить точними. Але всі ці методи є простими однокроковими методами, що потребують мінімальні затрати розрахункових ресурсів. Тому можна сказати, що методи Ейлера краще використовувати для попередніх(приблизних) розрахунків, а щоб отримати точний результат можна застосувати більш точний метод Рунге-Кутта.
Література
1. В.Т.Маликов, Р.Н.Кветный . Вычислительные методы и применение ЭВМ . Учебное пособие -- К.: Высш. шк. Главное издательство,1989.-213 с .
2. В.Е.Краскевич, К.Х.Зеленский, В.И.Гречко . Численные методы в инженерных исследованиях. -- К.: Высш. шк. Главное издательство, 1986.--263 с .
|