| МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
Кафедра “Обчислювальна техніка та програмування”
РГЗ
з курсу “
Основ
и конструювання
ЕОМ
”
Варіант №
xxx
Виконав:
Студент групи xxxxxx
xxxxxxxx.
Перевірив:
xxxxxxxxx.
Харків 2007
Задача № 1
Рассчитать и построить графики переходного процесса в «длинной» линии длиной 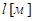 с волновым сопротивлением с волновым сопротивлением 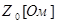 и погонной задержкой распространения и погонной задержкой распространения 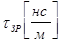 . Линия подключена к генератору с . Линия подключена к генератору с 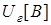 и и 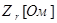 . Выход линии подключен к нагрузке . Выход линии подключен к нагрузке 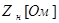 . Оценить время переходного процесса при . Оценить время переходного процесса при 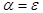 , считая переходный процесс законченным, когда , считая переходный процесс законченным, когда 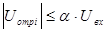 . . 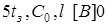
l
|
tзр
|
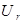
|
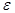
|
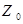
|
|
|
| 1,8
|
5,5
|
2
|
0,05
|
33
|
75
|
50
|
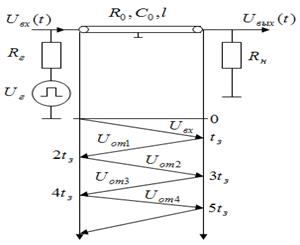
Решение
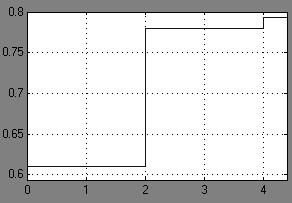
1. 1. 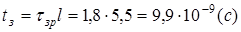
2. 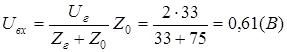
3. 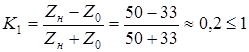
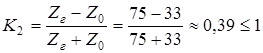
4.
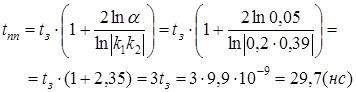
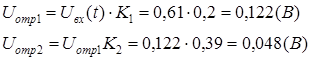
5.
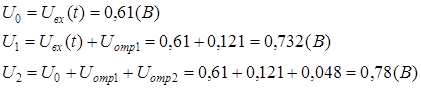
 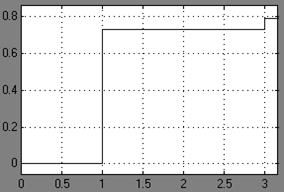
Задача № 2
Решить задачу №1 графически, используя метод Бержерона.
Решение
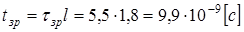
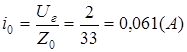
Zг
при iг
=0 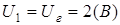
при i =i0 =i0
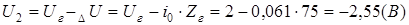
U1
[0;2] U2
[0,061;-2,55]
Zн
при iн
=0 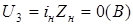 ; ;
при 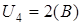 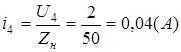
U3
[0;0] U4
[0,04;2]
Задача № 3
Определить неизвестный параметр при передаче импульсного сигнала по «длинной» линии в случае колебательного (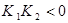 ) и апериодического характера ( ) и апериодического характера (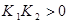 ) переходного процесса. ) переходного процесса.
| 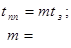
|
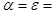
|
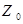 , Ом , Ом
|
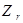 , Ом , Ом
|
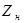 , Ом , Ом
|
| 11
|
0,1
|
60
|
525
|
?
|
Решение
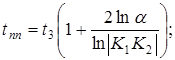 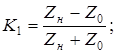 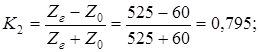
Найдем значение К1
для обоих случаев переходного процесса:
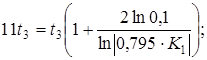
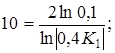
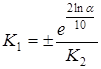
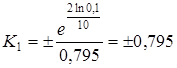
Вычислим сопротивление нагрузки Zн
:
1) При К1
=0,795 т.е. в случае апериодического характера переходного процесса:
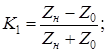 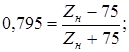 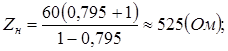
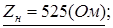
2) При К1
= - 0,795 т.е. в случае колебательного переходного процесса:
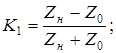 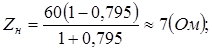
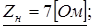
Ответ: При апериодическом характере переходного процесса 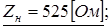
при колебательном характере переходного процесса 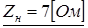 . .
Задача
№
4
Построить передний и задний фронты прямоугольного импульса (в начале и в конце линии), передаваемого по «длинной» линии с 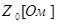 с выхода одной микросхемы на вход другой с учетом реальных вольтамперных характеристик микросхем (рис. 5.10 из книги: Савельев А. Я., Овчинников В. А. Конструирование ЭВМ и систем. М., ВШ, 1989 г., стр. 134). Из построенных графиков определить с выхода одной микросхемы на вход другой с учетом реальных вольтамперных характеристик микросхем (рис. 5.10 из книги: Савельев А. Я., Овчинников В. А. Конструирование ЭВМ и систем. М., ВШ, 1989 г., стр. 134). Из построенных графиков определить  и и 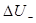 . .
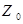 =33 Ом =33 Ом 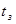 = =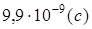
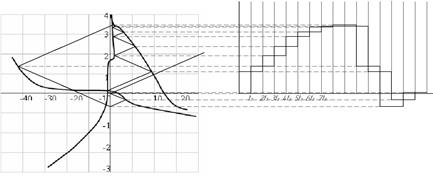
Ответ: 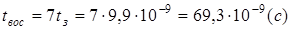 , , 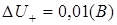 , , 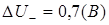 . .
Задача
№
5
Оценить минимальную задержку распространения сигнала между наиболее удаленными элементами устройства, которое предполагается выполнить в виде многорамной стойки прямоугольной формы. Рассчитать геометрические размеры стойки. В разрабатываемом устройстве количество микросхем N = 7000, объем корпуса микросхемы Vo
= 0,5cм3
, плотность компоновки оценивается коэффициентом заполнения объема kV
= 0,02, погонная задержка распространения сигнала tЗР
= 4 нс/м
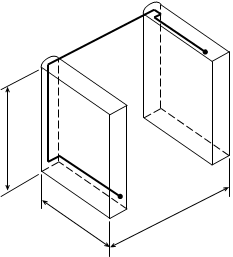
N = 7000
Vo
= 0,5 cм3
Реклама

kV
= 0,02
tЗР
= 4 нс/м
tЗ
min
Lb
, Lh
, Ll
Lh
Ll
Lb
Решение:
1. Объем устройства:
V = NVo
/ kV
= 7.
103.
0,5/0,04 = 175.
103
(см3
)
2. Длина линии связи (при k=0):
lсв
min
= 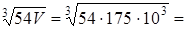 211 (см) 211 (см)
3. Минимальная задержка распространения сигнала:
tЗ
min
= lсв
min
.
tЗР
= 2,11.
4 = 8,46 (нс)
4. Длина, высота и ширина стойки соответственно (оценка получена снизу, так как lсв
min
определялась как минимальная длина линии связи между ТЭЗами):
Lb
= lсв
min
/ 6 = 211 / 6 = 35,2 (см)
Lh
= Ll
= lсв
min
/ 3 = 211 / 3 = 70,5 (см)
Ответ: tЗ
min
= 8,46 нс, Lb
= 0,35 м, Lh
= Ll
= 0,7 м
Задача
№
6
Рассчитать размеры основания панели и платы ТЭЗа и выбрать компоновочную схему панели. Длительность такта синхронизации функционального устройства, которое конструктивно оформляется в виде панели, Tc
= 30 нс; задержка сигнала между наиболее удаленными микросхемами устройства должна составлять не более 0,14Tc
.
Коэффициент трассировки kтр
=3,9.
 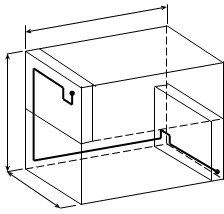 lb lb
Tc
= 30 нс
t3
= 0,18Tc
kтр
=3,9
lh
li
Решение:
1. Допустимая задержка сигнала в линии связи:
tЗ доп
= 0,14.
Tc
= 0,14.
30 = 4,2 (нс)
2. Так как внутрипараллельные связи выполнены печатными проводниками на многослойной печатной плате, примем tЗР
= 8 нс/м:
lсв доп
= tЗ доп
/ tЗР
= 4,2 / 8 = 0,525 (м)
3. Размеры основания панели:
l1
= l2
= lсв доп
/ 3 = 0,525 / 3 = 0,175 (м)
4. При коэффициенте трассировки kтр
= 3,9 длина ТЭЗа:
lт
= lсв доп
/ (3.
3,9)=0,525/ (3.
3,9) = 0,045 (м)
Расчет ширины платы ТЭЗа и выбор компоновочной схемы панели вычисляется для двух вариантов соотношения длины ТЭЗа к его ширине lТ
/bТ
.
Вариант 1. l Т
/b Т
=1. l 1
:l Т
=1:0.26, т.е l 1
=3,9bТ
.
Получаем однорядную компоновочную схему ТЭЗа.
Вариант 2. l Т
/b Т
=3/2, тогда получим l1
=5,85bТ
Получаем двурядную компоновочную схему ТЭЗа.
Задача №7
Оценить минимальную задержку распространения сигнала и геометрические размеры цилиндрической конструкции. В разрабатываемом устройстве количество микросхем N = 7000, объем корпуса микросхемы Vo
= 0,5 cм3
, плотность компоновки оценивается коэффициентом заполнения объема kV
= 0,02 , погонная задержка распространения сигнала tЗР
= 4 нс/м. Расчеты выполнить для двух вариантов: с неподвижными и вращающимися створками.
N = 7000
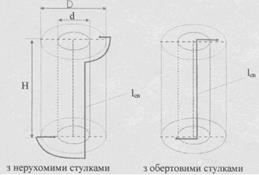
Vo
= 0,4 cм3
kV
= 0,02
tЗР
= 4 нс/м
Решение:
1. Объем створок (объем цилиндрической конструкции):
Vст
= NVo
/ kV
= 7.
103.
0,4/0,04 = 0,175.
(м3
)
2. При минимальных потерях в плотности компоновки:
Реклама

V = Vст
/ ( 1- P) = 0,175/(1-0,45) = 0.32 (м3
)
При неподвижных створках
3. Минимальная длина линии связи
lсв
min
= 3,24 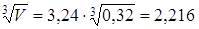 (м) (м)
4. Минимальная задержка распространения сигнала в линии связи:
tЗ
.
л
.
с
. min
= lсв
min
.
tЗР
= 2,216 .
4 = 8,86 (нс)
5. Высота и диаметр цилиндрической окружности:
H = D = lсв
min
/ 3 = 2,216/3 = 0,74(м)
D :h: d = 1: 0,5 : 0,577
h = 0,37 м, d= 0,43 м
При вращающихся створках
6. Минимальная длина линии связи
lсв
min
= 2,1 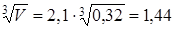 (м) (м)
7. Минимальная задержка распространения сигнала в линии связи:
tЗ
.
л
.
с
. min
= lсв
min
.
tЗР
= 1,44 .
4 = 5,75 (нс)
8. Высота и диаметр цилиндрической окружности:
H = D = lсв
min
/ 3 = 1,44/3 = 0,49(м)
D :h: d = 1: 0,5 : 0,577
h =0,245 м, d= 0,283 м
Ответ: При неподвижных створках: tЗ. л.с.
min
= 8,86 нс,
H = D = 0,74 м, h = 0,37 м, d= 0,43 м
При неподвижных створках: tЗ. л.с.
min
= 5,75 нс,
H = D = 0,49 м, h = 0,245 м, d= 0,283 м
Минимальная задержка сигнала между наиболее удаленными микросхемами цилиндрической окружности с вращающимися створками приблизительно на 35% меньше, чем с неподвижными.
Задача №8
Решить вопрос о применимости несогласованной линии связи между наиболее удаленными логическими элементами конструкции, выполненной в виде кабеля с волновым сопротивлением Z0
=300 Ом, погонной емкостью С0
=70 пФ/м при заданной паразитной емкости нагрузки Сн
=30 пФ и длительности фронта передаваемого сигнала tф
=10 нс. Заключение о применимости кабеля дать для каждой из трех задач.
Решение:
1. Решить данную задачу можно, используя для этого две формулы:
а) задержка распространения сигнала по линии связи на единицу длины для нагруженной линии
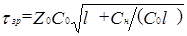 ; ;
б) предельная длина несогласованного соединения 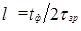 , следовательно , следовательно 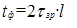 . .
2. Подставляя первое выражение во второе, получим квадратное уравнение и вычислим, решив его относительно l, предельную длину несогласованной линии:
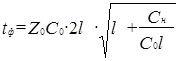 ; ;
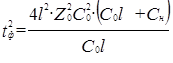 ; ;
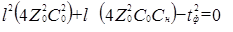 ; ;
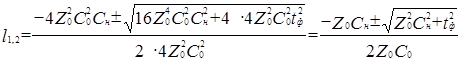 . .
Подставляя заданные значения, получим:
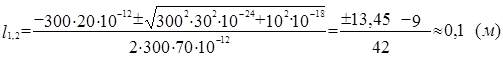 . .
Отрицательным значение допустимой длины быть не может, поэтому l=0,1 м.
3. Заключение о применимости заданного проводника для задач 5, 6 и 7 можно дать по следующим параметрам:
Проводник может применяться только для 6 задачи, так как:
- в первой задаче полученная длина проводника больше длины, полученной в этой задаче:
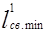 =2,11 м > =2,11 м > 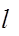 =0,1 м; =0,1 м;
- во второй задаче полученная в этой задаче допустимая длина проводника больше длины, полученной в этой задаче:
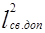 =0,525 м > =0,525 м > 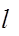 =0,1 м; =0,1 м;
- в третьей задаче полученная минимальная длина проводника больше длины, полученной в этой задаче:
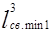 =2,216 м > =2,216 м > 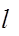 =0,1 м; =0,1 м;
 =1,44 м > =1,44 м > 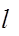 =0,1 м; =0,1 м;
Задача №9
Рассчитать допустимую длину линии связи между двумя ТТЛ-микросхемами, если известна допустимая задержка tз
max
импульсного сигнала в линии. Расчет выполнить для переднего и заднего фронтов импульса.
Решение
Случай 1. Индуктивный характер сигнальной связи.
Задержка по переднему фронту 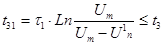 , где , где 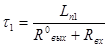 , ,
Lп1
= t1
.
(R0
вых
+ Rвх
) = L0
.
l1
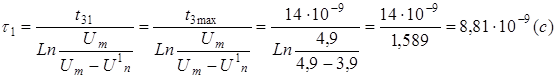
Lп1
= 8,81.
10 -9 .
(39 + 2400) = 21,5.
10 -6
(Гн)
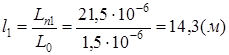
Задержка по заднему фронту 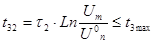 , где , где 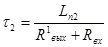
Lп2
= t2
.
( R1
вых
+ Rвх
) = L0
.
l2
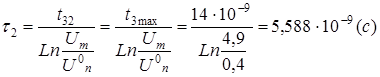
Lп2
= t2
.
(R1
вых
+ Rвх
) = 5,588.
10 -9 .
(230 + 2400) = 14,7.
10 -6
(Гн)
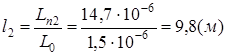
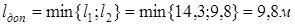
Случай 2. Емкостной характер сигнальной связи.
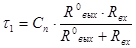
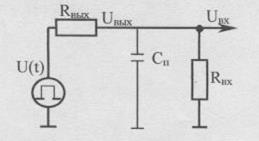
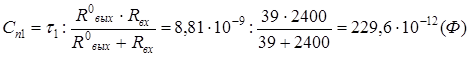
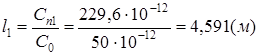
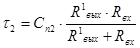
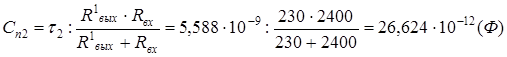
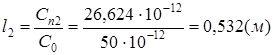
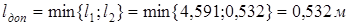
Ответ: Длина линии не должна превышать 9,8 (0,532) метра, поскольку размеры печатной платы таковы, что при любых комбинациях размещения микросхем длина связей между их выводами наверняка не превысит 9,8 (0,532) м, то ограничений на применение печатной платы предложенного размера нет.
Задача №10
В линии связи между ТТЛ-микросхемами МСх
1 и МСх
2 преобладает емкостная (случай 1) и индуктивная (случай 2) составляющая паразитных параметров линии связи. Определить неизвестные характеристики линии и импульсного сигнала, передаваемого по этой линии. Расчет выполнить отдельно для случая 1 и для случая 2. Дать заключение о применимости в качестве линии связи печатного проводника длиной l = 0,09 м с погонной емкостью C0
= 50 пФ/м (случай 1) или погонной индуктивностью L0
= 0,5.
10-6
Гн/м (случай 2)
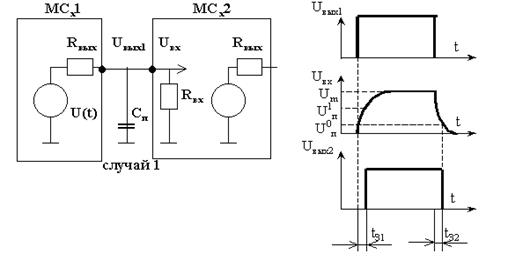 
U1
п
= 3,5 B
U0
п
= 0,4 В
Um
= 4,5 B
R1
вых
= 170 Oм
R0
вых
= 27 Ом
Rвх
= 1600 Ом
tЗ1
= 7.
10-9
с
С= ?
L = ?
tЗ2
= ?
Случай 1. Емкостная составляющая
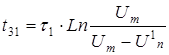
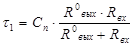
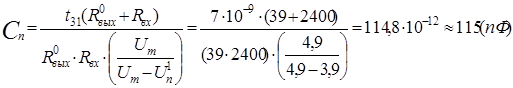
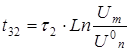
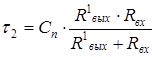
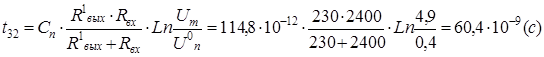
C*
п
= C0
.
l = 50.
10 -12 .
0,09 = 4,5.
10 -12
(Ф) С*
п
< Cп
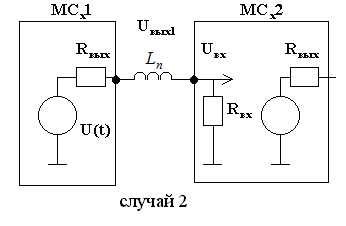
Случай 2. Индуктивная составляющая
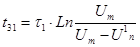
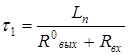
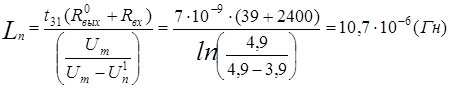
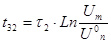
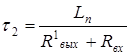
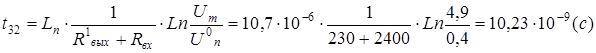
L*
п
= L0
.
l = 0,5.
10 -6 .
0,09 = 0,045.
10 -6
(Гн) L*
п
< Lп
Ответ: Cп
= 115 пФ, tЗ2
= 60,4 нс
Lп
= 10,7 мкГн, tЗ2
= 10,23 нс
Предложенный вариант исполнения линии связи в виде печатного проводника предпочтительнее исходного, поскольку собственные паразитные параметры проводника значительно меньше соответствующих параметров исходной линии связи (и в случае 1, и в случае 2).
|