Национальный научно-исследовательский университет
-ИрГТУ-
Кафедра прикладной геологии
Реферат по высшей математике
На тему: «Основные элементарные функции,
их свойства и графики»
Выполнил:
.
Проверил:
преподаватель
Коваленко Е.В.
Иркутск 2010
Содержание:
Показательные функции:- 3 -
Степенные функции:- 3 -
Логарифмические функции:- 3 -
Тригонометрические функции:- 3 -
Обратные тригонометрические функции:- 3 -
Список использованной литературы:- 3 -
Список рисунков:- 3 -
Показательные функции:
Определение. Функция, заданная формулой у=ах
(где а>0, а≠1), называется показательной функцией с основанием а.
Сформулируем основные свойства показательной функции :
1. Область определения — множество (R) всех действительных чисел.
2. Область значений — множество (R+) всех положительных действительных чисел.
3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает.
4. Является функцией общего вида.

Рис. 1 График функции
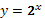 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]

Рис. 2 График функции
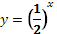 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]
Степенные функции:
Функция вида у(х)=хn
, где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).
Степенная функция у=х²
1. D(x)=R – функция определена на все числовой оси;
2. E(y)=[0;∞) - функция принимает положительные значения на всей области определения;
3. При х=0 у=0 - функция проходит через начало координат O(0;0).
4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
5. Функция является четной (симметрична относительно оси Оу).
В зависимости от числового множителя, стоящего перед х², функция может быть уже/шире и направлена вверх/вниз.
Реклама


Рис. 3 График функции
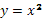 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]
Степенная функция у=х³
1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:
2. D(x)=R – функция определена на все числовой оси;
3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;
4. При х=0 у=0 – функция проходит через начало координат O(0;0).
5. Функция возрастает на всей области определения.
6. Функция является нечетной (симметрична относительно начала координат).

Рис. 4 График функции
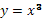 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]
В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.
Степенная функция с целым отрицательным показателем:
Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:
1. D(x)=(-∞;0)U(0;∞) для любого n;
2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;
3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.
4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.
5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

Рис. 5 График функции
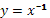 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]
Степенная функция с дробным показателем
Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)
1. D(x) ÎR, если n – нечетное число и D(x)=[0;∞), если n – четное число ;
2. E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;
3. Функция возрастает на всей области определения для любого числа n.
4. Функция проходит через начало координат в любом случае.

Рис. 6 График функции
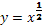 , на интервале xÎ [0;3] , на интервале xÎ [0;3]
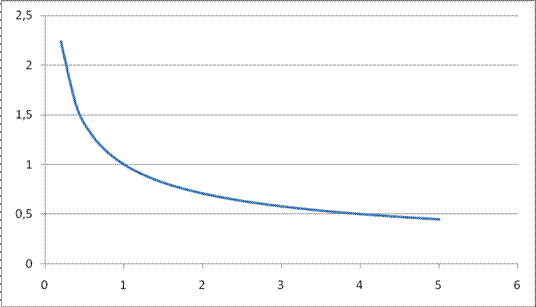
Рис. 7 График функции
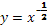 , на интервале xÎ [0;5] , на интервале xÎ [0;5]

Рис. 8 График функции
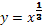 , на интервале xÎ [-3;3] , на интервале xÎ [-3;3]
Логарифмические функции:
Реклама

Логарифмическая функция у = loga
x обладает следующими свойствами :
1. Область определения D(x)Î (0; + ∞).
2. Область значений E(y) Î ( - ∞; + ∞)
3. Функция ни четная, ни нечетная (общего вида).
4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.
График функции у = loga
x может быть получен из графика функции у = ах
с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.
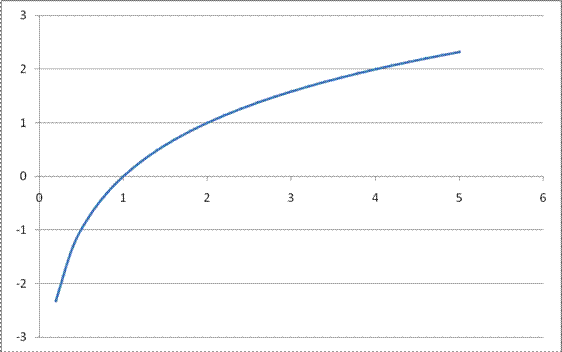
Рис. 9 График функции
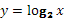 ; на интервале xÎ [0;5] ; на интервале xÎ [0;5]

Рис. 10 График функции
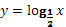 ; на интервале xÎ [0;5] ; на интервале xÎ [0;5]
Тригонометрические функции:
Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.
Функция y = sin (х).
1. Область определения D(x) ÎR.
2. Область значений E(y) Î [ - 1; 1].
3. Функция периодическая; основной период равен 2π.
4. Функция нечетная .
5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.
График функции у = sin (х) изображен на рисунке 11.
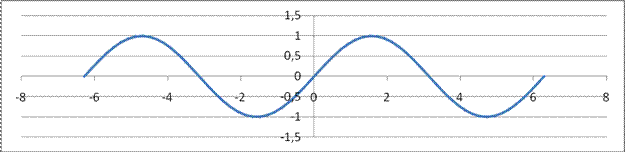
Рис. 11 График функции
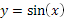 ; на интервале xÎ [-2 ; на интервале xÎ [-2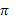 ;2 ;2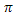 ] ]
Функция y = cos(х).
1. Область определения D(x) ÎR.
2. Область значений E(y) Î [ - 1; 1].
3. Функция периодическая с основным периодом 2π.
4. Функция четная.
5. Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.
График функции у = соs (х) изображен на рисунке 12.
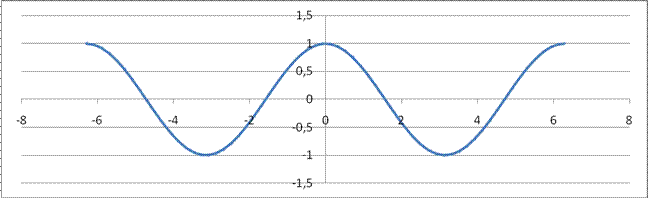
Рис. 12 График функции
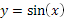 ; на интервале xÎ [-2 ; на интервале xÎ [-2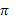 ;2 ;2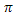 ] ]
Функция y = tg х.
1. Область определения: D(x) Ï π/2 + πk, kÎZ.
2. Область значений E(y) Î (- ∞; + ∞)
3. π- основной период функции.
4. Функция нечетная.
5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).
График функции у = tg х изображен на рисунке 13.
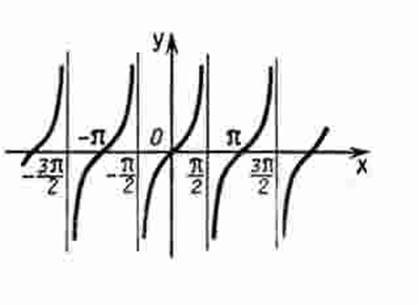
Рис. 13 График функции
 ; на интервале xÎ (- ; на интервале xÎ (-  ; ; ) )
Функция y = ctg х.
1. Область определения функции: D(x) Ï xπ/2 +πk, kÎZ.
2. Область значений функции E(y) Î (- ∞; + ∞).
3. Функция периодическая с основным периодом π.
4. Функция нечетная.
5. Функция у = ctg х убывает на промежутках (πn;π+πn).
График функции у = ctg х изображен на рисунке 14.
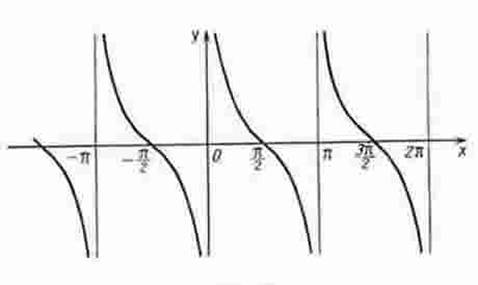
Рис. 14 График функции
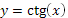 ; на интервале xÎ (-𝜋;) ; на интервале xÎ (-𝜋;)
Обратные тригонометрические функции:
Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.
Функция
y
=
arcsin
(
x
):
Свойства функции y = arcsin (x):
1. Область определения D(x)Î[−1;1]
2. Область значения E(y)Î [−π/2;π/2]
3. y=arcsin(x)- непрерывная строговозрастающая функция на D
5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x
6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)
График функции y = arcsin (x) изображен на рисунке 15.
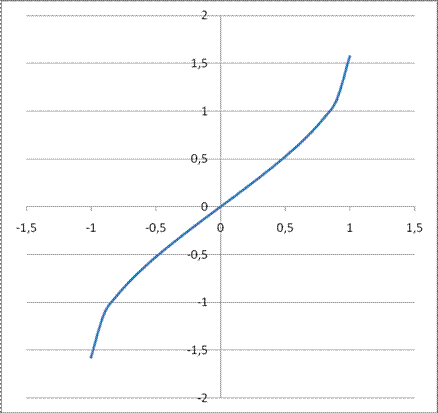
Рис. 15 График функции
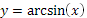 ; на интервале xÎ [- ; на интервале xÎ [- 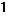 ;] ;]
Функция
y
=
arccos
(
x
):
Свойства функции y = arccos (x):
1. Область определения D(x)Î[−1;1]
2. Область значения E(y)Î [0;π]
3. y=arccos(x)- непрерывная строговозрастающая функция на D
5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x
6. y=arccos(x) функция общего вида
График функции y = arccos (x) изображен на рисунке 16.
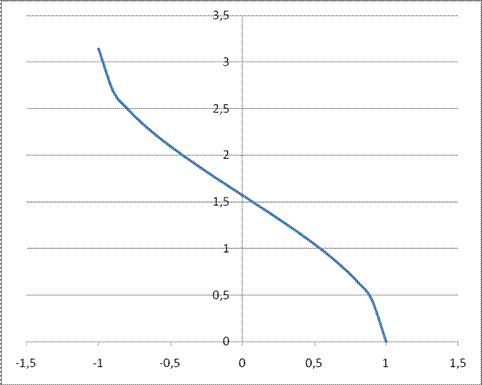
Рис. 16 График функции
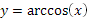 ; на интервале xÎ [- ; на интервале xÎ [-  ;] ;]
Функция
y
=
arctg
(
x
):
Свойства функции y = arctg (x):
1. Область определения D(x)Î(- ∞;+∞)
2. Область значения E(y)Î [−π/2;π/2]
3. y=arctg (x)- непрерывная строговозрастающая функция на D
4. График y = arctg(x) симметричен графику y = tg(x) относительно линии y=x
5. y=arctg(x) нечетная функция.
График функции y = arctg (x) изображен на рисунке 17.
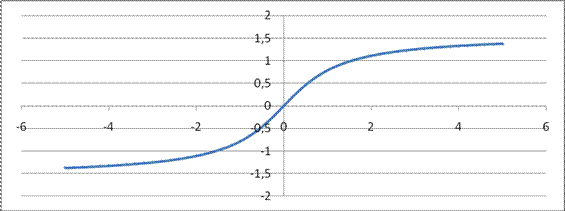
Рис. 17 График функции
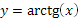 ; на интервале xÎ [- 5; 5] ; на интервале xÎ [- 5; 5]
Функция
y
=
arc
с
tg
(
x
):
Свойства функции y = arcсtg (x):
1. Область определения D(x)Î(- ∞;+∞)
2. Область значения E(y)Î [0 ; π]
3. y=arctg (x)- непрерывная строгоубывающая функция на D
4. График y = arcсtg(x) симметричен графику y = сtg(x) относительно линии y=x
5. y=arcctg(x) функция общего вида.
График функции y = arcctg (x) изображен на рисунке 18.
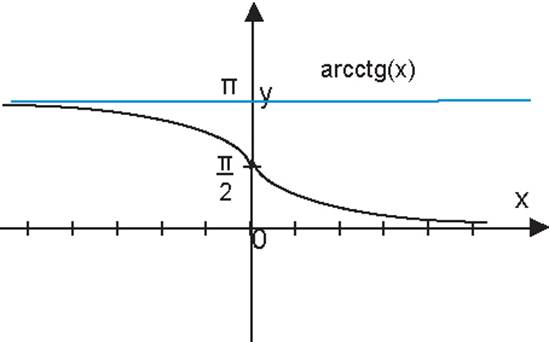
Рис. 18 График функции
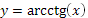 . .
Список использованной литературы:
1. Алгебра и начала анализа, учебник для 10 класса общеобразовательных учреждений ; С.М. Никольский; М. Просвещение, 2001
2. Конспект лекции по высшей математике.
Некоторые изображения взяты из сети Интернет, графики функции построены в программе MicrosoftOfficeExel.
Список рисунков:
Рис. 1 График функции 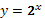 , на интервале xÎ [-3;3] ………………………- 3 - , на интервале xÎ [-3;3] ………………………- 3 -
Рис. 2 График функции 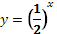 , на интервале xÎ [-3;3]..…………………..- 3 - , на интервале xÎ [-3;3]..…………………..- 3 -
Рис. 3 График функции 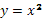 , на интервале xÎ [-3;3] ………………………- 3 - , на интервале xÎ [-3;3] ………………………- 3 -
Рис. 4 График функции 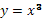 , на интервале xÎ [-3;3]………………………- 3 - , на интервале xÎ [-3;3]………………………- 3 -
Рис. 5 График функции 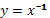 , на интервале xÎ [-3;3] …………………......- 3 - , на интервале xÎ [-3;3] …………………......- 3 -
Рис. 6 График функции 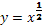 , на интервале xÎ [0;3] ………………………..- 3 - , на интервале xÎ [0;3] ………………………..- 3 -
Рис. 7 График функции 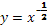 , на интервале xÎ [0;5] ……..………………..- 3 - , на интервале xÎ [0;5] ……..………………..- 3 -
Рис. 8 График функции 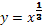 , на интервале xÎ [-3;3] …………………...…..- 3 - , на интервале xÎ [-3;3] …………………...…..- 3 -
Рис. 9 График функции 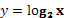 ; на интервале xÎ [0;5]…………………...- 3 - ; на интервале xÎ [0;5]…………………...- 3 -
Рис. 10 График функции 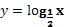 ; на интервале xÎ [0;5] …………..……...- 3 - ; на интервале xÎ [0;5] …………..……...- 3 -
Рис. 11 График функции 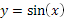 ; на интервале xÎ [-2 ; на интервале xÎ [-2 ;2 ;2 ] …………..- 3 - ] …………..- 3 -
Рис. 12 График функции 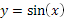 ; на интервале xÎ [-2 ; на интервале xÎ [-2 ;2 ;2 ] …………..- 3 - ] …………..- 3 -
Рис. 13 График функции 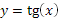 ; на интервале xÎ (- ;) ………..- 3 - ; на интервале xÎ (- ;) ………..- 3 -
Рис. 14 График функции 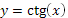 ; на интервале xÎ (-𝜋;) ……………- 3 - ; на интервале xÎ (-𝜋;) ……………- 3 -
Рис. 15 График функции 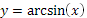 ; на интервале xÎ [- ; на интервале xÎ [-  ;] ………...- 3 - ;] ………...- 3 -
Рис. 16 График функции 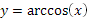 ; на интервале xÎ [- ; на интервале xÎ [-  ;] ………..- 3 - ;] ………..- 3 -
Рис. 17 График функции 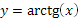 ; на интервале xÎ [- 5; 5] ………….- 3 - ; на интервале xÎ [- 5; 5] ………….- 3 -
Рис. 18 График функции 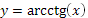 . ……………………………………..- 3 - . ……………………………………..- 3 -
|