Министерство образования и науки Украины
Государственная лётная академия
Теория вероятностей
и математическая статистика
Лабораторная работа№1
Статистическая устойчивость случайных событий.
Вариант 6
Выполнил:
Курсант 871 к.о.
Зозуля С.
Проверил:
Борота В.Г.
Кировоград 2009 г.
1.
Краткие теоретические сведения.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие “при бросании монеты выпал герб” – случайное . Каждое случайное событие, в частности выпадение герба, есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны.
По иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определённым закономерностям, а именно вероятностным закономерностям.
Пусть произошло n испытаний, и событие А произошло m раз. Очевидно, что 0£m£n.
Частотой случайного события А в данной последовательности испытаний называется число W(A) где
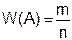
т.е. отношение количества появлений события А к количеству испытаний.
Событие А называется статистически устойчивым, если при увеличении числа испытаний n частота W(A) стабилизируется и стремится к определенному числу Р почти в каждой серии испытаний. Для проверки статистической устойчивости случайного события А можно построить последовательность значений частоты W(A) при n®¥ и изобразить последовательность на графике. Если W(A) при n®¥ группируется около определённого числа Р, можно предположить устойчивость частоты события А.
Статистическое определение вероятности: вероятностью случайного события А называется такое число Р=Р(А), что частота W(А) стремится к Р при увеличении числа испытаний n почти в каждой серии испытаний.
Реклама

Классическое определение вероятности: вероятностью события А называется отношение числа благоприятствующих этому событию исходов m к общему числу всех равновозможных несовместных элементарных исходов n, образующих полную группу.
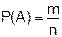
Произведем n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна Р (0<p<1).
Величина
q = 1- p
является вероятностью события Ā, противоположного событию А, заключающегося в не появлении события А
q = p (Ā)
Поставим перед собой задачу найти вероятность того, что отклонения относительной частоты 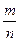 от постоянной вероятности р по абсолютной величине не превышает заданного числа e>0. Другими словами, найдем вероятность осуществления неравенства от постоянной вероятности р по абсолютной величине не превышает заданного числа e>0. Другими словами, найдем вероятность осуществления неравенства 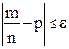 . .
Эту вероятность будем обозначать так:
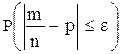
Можно доказать, что
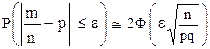
Здесь
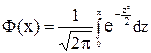
функция Лапласа.
При решении задач пользуются специальными таблицами, так как неопределенный интеграл 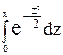 не выражается через элементарные функции. В таблице даны значения Φ(x) для положительных значений x и для x = 0; для х< 0 пользуются той же таблицей, поскольку функция Φ(x) – нечетная, Φ(-x)= - Φ(x). не выражается через элементарные функции. В таблице даны значения Φ(x) для положительных значений x и для x = 0; для х< 0 пользуются той же таблицей, поскольку функция Φ(x) – нечетная, Φ(-x)= - Φ(x).
В таблице приведены значения интеграла только для x = 5, так как для x>5 можно принять Φ(x)=0,5.
Доверительная вероятность:
Пусть найденная по данным серии опытов статистическая характеристика W(A) служит оценкой неизвестного параметра Р(А). Ясно, что W(A) тем точнее определять параметр Р(А), чем меньше абсолютная величина разности÷Р(А)-W(А)÷. Другими словами, если
÷Р(А)-W(А)÷<e, то чем меньше e, тем оценка точнее. Таким образом, положительное число e характеризует точность оценки.
Надёжностью или доверительной вероятностью оценки Р(А) по W(А) называют вероятность γ, с которой осуществляется неравенство
÷Р(А)-W(А)÷<e
Обычно надёжность оценки задаётся наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,9; 0,95; 0,99 и 0,999. Если нужно оценить минимальное число опытов, необходимое для стабильного получения отклонений частоты в пределах заданной величины e, то для доверительной вероятности γ =0,95 можно пользоваться формулой
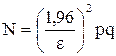
Варианты задач для заданий 1 и 2
Задача 1.
Событие А – появление герба при бросании монеты. Результаты опытов отражены в приложении 1. Серии брать по 10 бросаний монеты. Последовательность испытаний указана в таблице заданий.
Реклама

Задача 2.
Событие А – регистрация мальчиков среди новорожденных. Результаты опытов отражены в приложении 2. Серии брать по 10 регистраций. Последовательность испытаний указана в таблице заданий.
Задача 3.
Событие А – поступление в КИСМ абитуриентов с фамилией, начинающейся с буквы К. Результаты опытов отражены в прил. 3. Серии брать по числу студентов в группах. Последовательность опытов -в таблице заданий.
Задача 4 .
Событие А – появление цифры 1,2,3,4,5 или 6 при бросании игрального кубика. Результаты опытов отражены в приложении 4. Серии брать по 30 бросаний кубика. Последовательность испытаний и цифра указаны в таблице заданий.
Задача 5.
Сделать вырезку из газеты или журнала. Событие А – появление буквы в тексте. В отрывке должно быть 2000 букв. Серии брать по 100 букв. Необходимая буква указана в таблице заданий. Вероятности появлений русских букв в тексте в приложении 11.
Таблица заданий
| Номер |
Номер задачи |
Последовательность |
Вариант буквы |
| варианта |
для задания 1 |
испытаний |
для задания 2 |
| 1 |
1 |
1-300 |
Задача 5 - "О" |
| 2 |
1 |
101-400 |
Задача 5 - "И" |
| 3 |
1 |
201-500 |
Задача 5 - "А" |
| 4 |
1 |
301-600 |
Задача 5 - "Е" |
| 5 |
1 |
401-700 |
Задача 5 - "О" |
| 6 |
1 |
501-800 |
Задача 5 - "И" |
| 7 |
2 |
1-360 |
Задача 5 - "А" |
| 8 |
2 |
121-480 |
Задача 5 - "Е" |
| 9 |
2 |
241-600 |
Задача 5 - "О" |
| 10 |
2 |
351-720 |
Задача 5 - "И" |
| 11 |
2 |
481-840 |
Задача 5 - "А" |
| 12 |
2 |
601-960 |
Задача 5 - "Е" |
| 13 |
2 |
721-1080 |
Задача 5 - "О" |
| 14 |
3 |
С01-Д91 |
Задача 5 - "И" |
| 15 |
3 |
Д91-Р83 |
Задача 5 - "А" |
| 16 |
4 |
1-600 цифра 6 |
Задача 5 - "Е" |
| 17 |
4 |
1-600 цифра 5 |
Задача 5 - "О" |
| 18 |
4 |
1-600 цифра 4 |
Задача 5 - "И" |
| 19 |
4 |
1-600 цифра 3 |
Задача 5 - "А" |
| 20 |
4 |
1-600 цифра 2 |
Задача 5 - "Е" |
| 21 |
4 |
1-600 цифра 1 |
Задача 5 - "О" |
| 22 |
4 |
301-900 цифра 6 |
Задача 5 - "И" |
| 23 |
4 |
301-900 цифра 5 |
Задача 5 - "А" |
| 24 |
4 |
301-900 цифра4 |
Задача 5 - "Е" |
| 25 |
4 |
301-900 цифра 3 |
Задача 5 - "О" |
| 26 |
4 |
301-900 цифра 2 |
Задача 5 - "И" |
| 27 |
4 |
301-900 цифра 1 |
Задача 5 - "А" |
| 28 |
4 |
451-1050 цифра 6 |
Задача 5 - "Е" |
| 29 |
4 |
451-1050 цифра 5 |
Задача 5 - "О" |
| 30 |
4 |
451-1050 цифра 4 |
Задача 5 - "И" |
Задания к лабораторной работе.
1.Для изучения статистической устойчивости события А в заданиях 1 и 2 результаты испытаний сгруппировать сериями по n испытаний в каждой серии, Число полученных серий обозначим k
.
2.Подсчитать число появлений mі
события А в каждой серии.
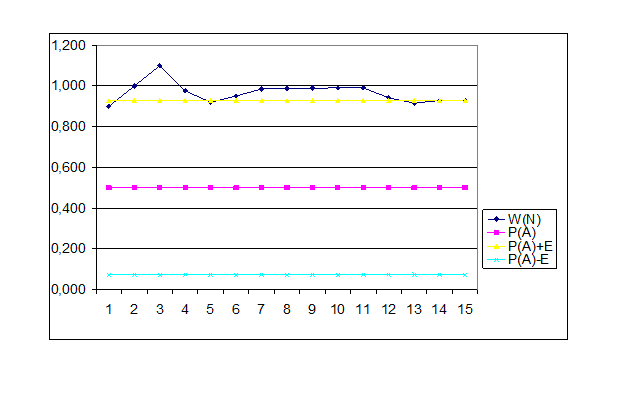
3.Вычислить частоту ωi
(A) появления событий А в каждой серии/
4.Объединив результаты опытов 1 и 2, затем 1, 2, 3 и т.д. до последней серии опытов в задании, вычислить:
Nі
– число опытов в объединённых (накопленных) сериях испытаний.
Mі
– число появления события А в объединенных (накопленных) сериях
испытаний.
Wі
(А) – частоту появления события А в объединенных (накопленных) сериях испытаний.
5. Результаты вычислений занести в таблицу 1.
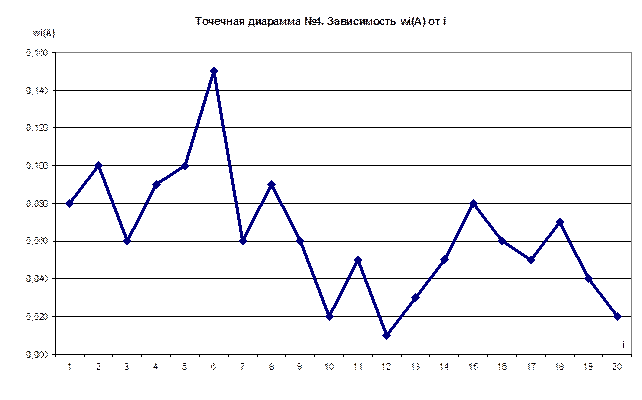
6. Построить точечную диаграмму №1. Зависимость ωi
(A) от номера серииі=1, 2, ... k.
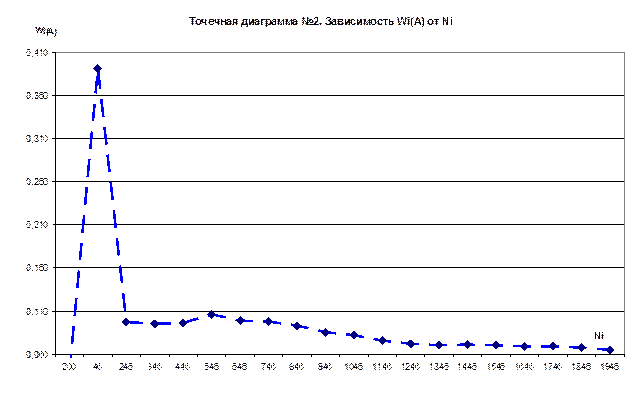
7.Построить точечную диаграмму №2. Зависимость Wk
(А)от числа опытов в серии Nі
.
8. Сравнить полученные диаграммы и сделать вывод о статической устойчивости события А.
9. Вычислить или найти в приложении 1 и 2 вероятность появления события А Р(А).
10. Вычислить вероятность противоположного события, пользуясь формулой q = 1 -p.
11.Найти отклонение относительной частоты Wk(А) от его статистической вероятности Р(А), пользуясь формулой e=÷Wk
(А)-Р(А)÷.
12.Изобразить на точечной диаграмме №2 линии, соответствующие значениям Р(А),Р(А)+e и Р(А)-e.
13. Вычислить вероятность того, что отклонение относительной частоты 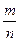 от постоянной вероятности р по абсолютной величине не превышает заданного числа e>0.
от постоянной вероятности р по абсолютной величине не превышает заданного числа e>0.
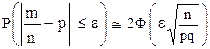
14. Определить, находится ли в пределах заданной величины e отклонение частоты Wk
(А) от его статистической вероятности Р(А).
15.Оценить минимальное число опытов, необходимых для стабильного получения отклонений частоты Wk
(А) от его статистической вероятности Р(А)в пределах заданной величины e, для доверительной вероятности γ = 0,95 по формуле
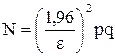
16.Сделать выводы.
Замечания
1.Все вычисления производить с точностью до 0,001.
2.Точечные диаграммы строить на миллиметровой бумаге, выбирая масштаб в зависимости от полученных числовых значений величины Wі
(А).
Контрольные вопросы.
1. Какие события называются случайными?
2. Что называется частотой случайного события А?
3. Какое событие называется статистически устойчивым?
4. Сформулировать статистическое определение вероятности.
5. Сформулировать классическое определение вероятности.
6. Как определить вероятность отклонения частоты W(A) случайного события А от его вероятности Р(А) в независимых испытаниях?
7. Какая функция называется функцией Лапласа? Сформулировать свойства функции Лапласа.
8. Как найти вероятность события противоположного событию А?
9. Что называется доверительной вероятностью или надежностью оценки характеристики W(A)?
10. Как определить минимальное число опытов, необходимых для стабильного получения отклонений частоты W(A) в пределах заданной доверительной вероятности?
задача № 1
Задача 1
Событие А – появление герба при бросании монеты. Результаты опытов отражены в приложении 1. Серии брать по 10 бросаний монеты. Последовательность испытаний и цифра указаны в таблице заданий.
Решение.
1. Результаты испытаний сгруппируем в k=15 серий по n=10 испытаний в каждой серии.
2. Заполним первую колонку таблицы "№ серии". Для этого проставляем номера серий от 1 до 15,
3. Заполним вторую колонку таблицы "Число испытаний в серии". В каждой серии по n=10 испытаний.
4. Подсчитаем числопоявление герба при бросании монеты в каждой серии. Данные занесем в третью колонку " Появление герба при бросании монеты в серии".
5. Вычислим частоту ωi
(А) появления герба при бросании монеты в каждой серии. Для этого поделим появление герба при бросании монеты на количество испытаний в серии.
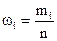
6. Объединяем результаты опытов всех 15-ти серий.
7. Вычисляем появление герба при бросании монеты в объединенной серии: Мі
.
8. Вычисляем Wk
(А) – частоту появление герба при бросании монеты в объединенных сериях испытаний.
9. Построим точечную диаграмму №1 "Зависимость ωi
(A) от номера серии і=1, 2, ... k".
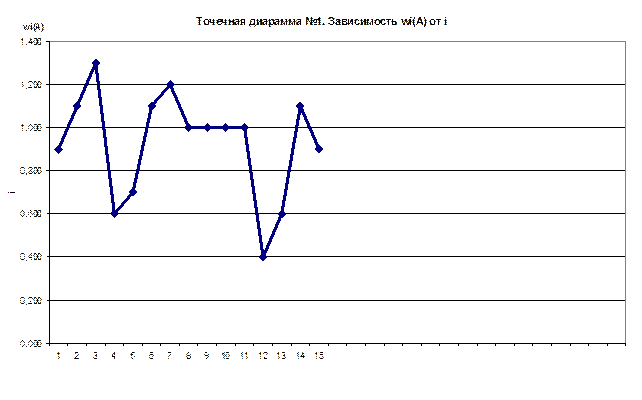
10. Строим точечную диаграмму №2 "Зависимость Wk
(А) от числа опытов в объединенной серии Nk
".
11. Находим в приложении 1 появления герба при бросании монеты.
Р(А) = 0,5
12. Вычисляем вероятность противоположного события, пользуясь формулой
q = 1 - p
q = 1 - 0,5 = 0,5
13. Находим отклонение относительной частоты Wk
(А) от вероятности Р(А) = 0,5, пользуясь формулой e=÷Wk
(А) - Р(А)÷
e =÷ 0,927 – 0,5÷ = 0,427
Изобразим на точечной диаграмме № 2 линии, соответствующие значениям
Р(А)= 0,5
Р(А)+e= 0,5 + 0,427 =0,927
Р(А) - e= 0,5 – 0,427 = 0,073
Вычисляем вероятность того, что отклонение относительной частоты 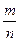 от постоянной вероятности р по абсолютной величине не превышает заданного числа e> 0.
от постоянной вероятности р по абсолютной величине не превышает заданного числа e> 0.
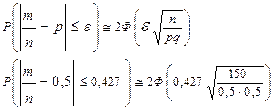
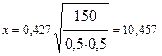
Отметим, что отклонение частоты Wk
(А) от вероятности Р(А) = 0,5 находится в пределах найденной величины e= 0,427.
17. Сравниваем полученные диаграммы и делаем вывод о статистической устойчивости события А - появление герба при бросании монеты.
18. Оценим минимальное число опытов, необходимых для стабильного получения отклонений частоты Wk
(А) от вероятности Р(А) в пределах заданной величины e= 0,427, для доверительной вероятности γ = 0,95 по формуле
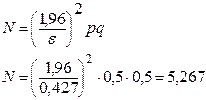
Выводы к задаче №1
1.Проведя 15 серий опытов по 10 опытов в каждой серии и построив точечную диаграмму зависимости частоты ωi
(A) от номера серии, заметим, что число опытов не достаточно для определения статистической устойчивости случайного события А – появления герба при бросании монеты.
2.Проведя 150 опытов и построив точечную диаграмму зависимости накопленной частоты Wk
(А) от количества испытаний, убеждаемся, что событие А - появление герба при бросании монеты, является статистически устойчивым, поскольку с увеличением числа опытов накопленная частота стабилизируется и стремится к числу
Wk
(А) = 0,053
3. Вероятность отклонения частоты W k (А) случайного события А от его статистической вероятности Р(А) = 0,5 на величину e = 0,427 равна Р = 0,5.
4. Минимальное число опытов, необходимых для стабильного получения отклонений частоты Wk
(А) от вероятности Р(А) в пределах заданной величины e= 0,427 для доверительной вероятности γ = 0,95.
N = 5,267
Таблица № 1
| № серии
|
ni - число испытаний в серии
|
mi - число появлений события А
|
wi(A) - частота появления события А
|
Ni - число испытаний в объединённой серии
|
Mi - число появления события А в объединённой серии
|
Wi(A) - частота появления события А в объединённой серии
|
P(A)
|
ε = |W-P|
|
P(A)+ε
|
P(A)-ε
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| 1 |
10 |
9 |
0,900 |
10 |
9 |
0,900 |
0,500 |
0,427 |
0,927 |
0,073 |
| 2 |
10 |
11 |
1,100 |
20 |
20 |
1,000 |
0,500 |
0,427 |
0,927 |
0,073 |
| 3 |
10 |
13 |
1,300 |
30 |
33 |
1,100 |
0,500 |
0,427 |
0,927 |
0,073 |
| 4 |
10 |
6 |
0,600 |
40 |
39 |
0,975 |
0,500 |
0,427 |
0,927 |
0,073 |
| 5 |
10 |
7 |
0,700 |
50 |
46 |
0,920 |
0,500 |
0,427 |
0,927 |
0,073 |
| 6 |
10 |
11 |
1,100 |
60 |
57 |
0,950 |
0,500 |
0,427 |
0,927 |
0,073 |
| 7 |
10 |
12 |
1,200 |
70 |
69 |
0,986 |
0,500 |
0,427 |
0,927 |
0,073 |
| 8 |
10 |
10 |
1,000 |
80 |
79 |
0,988 |
0,500 |
0,427 |
0,927 |
0,073 |
| 9 |
10 |
10 |
1,000 |
90 |
89 |
0,989 |
0,500 |
0,427 |
0,927 |
0,073 |
| 10 |
10 |
10 |
1,000 |
100 |
99 |
0,990 |
0,500 |
0,427 |
0,927 |
0,073 |
| 11 |
10 |
10 |
1,000 |
110 |
109 |
0,991 |
0,500 |
0,427 |
0,927 |
0,073 |
| 12 |
10 |
4 |
0,400 |
120 |
113 |
0,942 |
0,500 |
0,427 |
0,927 |
0,073 |
| 13 |
10 |
6 |
0,600 |
130 |
119 |
0,915 |
0,500 |
0,427 |
0,927 |
0,073 |
| 14 |
10 |
11 |
1,100 |
140 |
130 |
0,929 |
0,500 |
0,427 |
0,927 |
0,073 |
| 15 |
10 |
9 |
0,900 |
150 |
139 |
0,927 |
0,500 |
0,427 |
0,927 |
0,073 |


Таблица значений функции Ф (х
) = 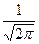 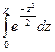
| х
|
Ф (х
) |
х
|
Ф (х
) |
х
|
Ф (х
) |
х
|
Ф (х
) |
| 0,00 |
0,0000 |
0,24 |
0,0948 |
0,48 |
0,1844 |
0,72 |
0,2642 |
| 0,01 |
0,0040 |
0,25 |
0,0987 |
0,49 |
0,1879 |
0,73 |
0,2673 |
| 0,02 |
0,0080 |
0,26 |
0,1026 |
0,50 |
0,1915 |
0,74 |
0,2703 |
| 0,03 |
0,0120 |
0,27 |
0,1064 |
0,51 |
0,1950 |
0,75 |
0,2734 |
| 0,04 |
0,0160 |
0,28 |
0,1103 |
0,52 |
0,1985 |
0,76 |
0,2764 |
| 0,05 |
0,0199 |
0,29 |
0,1141 |
0,53 |
0,2019 |
0,77 |
0,2794 |
| 0,06 |
0,0239 |
0,30 |
0,1179 |
0,54 |
0,2054 |
0,78 |
0,2823 |
| 0,07 |
0,0279 |
0,31 |
0,1217 |
0,55 |
0,2088 |
0,79 |
0,2852 |
| 0,08 |
0,0319 |
0,32 |
0,1255 |
0,56 |
0,2123 |
0,80 |
0,2881 |
| 0,09 |
0,0359 |
0,33 |
0,1293 |
0,57 |
0,2157 |
0,81 |
0,2910 |
| 0,10 |
0,0398 |
0,34 |
0,1331 |
0,58 |
0,2190 |
0,82 |
0,2939 |
| 0,11 |
0,0438 |
0,35 |
0,1368 |
0,59 |
0,2224 |
0,83 |
0,2967 |
| 0,12 |
0,0478 |
0,36 |
0,1406 |
0,60 |
0,2257 |
0,84 |
0,2995 |
| 0,13 |
0,0517 |
0,37 |
0,1443 |
0,61 |
0,2291 |
0,85 |
0,3023 |
| 0,14 |
0,0557 |
0,38 |
0,1480 |
0,62 |
0,2324 |
0,86 |
0,3051 |
| 0,15 |
0,0596 |
0,39 |
0,1517 |
0,63 |
0,2357 |
0,87 |
0,3078 |
| 0,16 |
0,0636 |
0,40 |
0,1554 |
0,64 |
0,2389 |
0,88 |
0,3106 |
| 0,17 |
0,0675 |
0,41 |
0,1591 |
0,65 |
0,2422 |
0,89 |
0,3133 |
| 0,18 |
0,0714 |
0,42 |
0,1628 |
0,66 |
0,2454 |
0,90 |
0,3159 |
| 0,19 |
0,0753 |
0,43 |
0,1664 |
0,67 |
0,2486 |
0,91 |
0,3186 |
| 0,20 |
0,0793 |
0,44 |
0,1700 |
0,68 |
0,2517 |
0,92 |
0,3212 |
| 0,21 |
0,0832 |
0,45 |
0,1736 |
0,69 |
0,2549 |
0,93 |
0,3238 |
| 0,22 |
0,0871 |
0,46 |
0,1772 |
0,70 |
0,2580 |
0,94 |
0,3264 |
| 0,23 |
0,0910 |
0,47 |
0,1808 |
0,71 |
0,2611 |
0,95 |
0,3289 |
| 0,96 |
0,3315 |
1,37 |
0,4147 |
1,78 |
0,4625 |
2,36 |
0,4909 |
| 0,97 |
0,3340 |
1,38 |
0,4162 |
1,79 |
0,4633 |
2,38 |
0,4913 |
| 0,98 |
0,3365 |
1,39 |
0,4177 |
1,80 |
0,4641 |
2,40 |
0,4918 |
| 0,99 |
0,3389 |
1,40 |
0,4192 |
1,81 |
0,4649 |
2,42 |
0,4922 |
| 1,00 |
0,3413 |
1,41 |
0,4207 |
1,82 |
0,4656 |
2,44 |
0,4927 |
| 1,01 |
0,3438 |
1,42 |
0,4222 |
1,83 |
0,4664 |
2,46 |
0,4931 |
| 1,02 |
0,3461 |
1,43 |
0,4236 |
1,84 |
0,4671 |
2,48 |
0,4934 |
| 1,03 |
0,3485 |
1,44 |
0,4251 |
1,85 |
0,4678 |
2,50 |
0,4938 |
| 1,04 |
0,3508 |
1,45 |
0,4265 |
1,86 |
0,4686 |
2,52 |
0,4941 |
| 1,05 |
0,3531 |
1,46 |
0,4279 |
1,87 |
0,4693 |
2,54 |
0,4945 |
| 1,06 |
0,3554 |
1,47 |
0,4292 |
1,88 |
0,4699 |
2,56 |
0,4948 |
| 1,07 |
0,3577 |
1,48 |
0,4306 |
1,89 |
0,4706 |
2,58 |
0,4951 |
| 1,08 |
0,3599 |
1,49 |
0,4319 |
1,90 |
0,4713 |
2,60 |
0,4953 |
| 1,09 |
0,3621 |
1,50 |
0,4332 |
1,91 |
0,4719 |
2,62 |
0,4956 |
| 1,10 |
0,3643 |
1,51 |
0,4345 |
1,92 |
0,4726 |
2,64 |
0,4959 |
| 1,11 |
0,3665 |
1,52 |
0,4357 |
1,93 |
0,4732 |
2,66 |
0,4961 |
| 1,12 |
0,3686 |
1,53 |
0,4370 |
1,94 |
0,4738 |
2,68 |
0,4963 |
| 1,13 |
0,3708 |
1,54 |
0,4382 |
1,95 |
0,4744 |
2,70 |
0,4965 |
| 1,14 |
0,3729 |
1,55 |
0,4394 |
1,96 |
0,4750 |
2,72 |
0,4967 |
| 1,15 |
0,3749 |
1,56 |
0,4406 |
1,97 |
0,4756 |
2,74 |
0,4969 |
| 1,16 |
0,3770 |
1,57 |
0,4418 |
1,98 |
0,4761 |
2,46 |
0,4971 |
| 1,17 |
0,3790 |
1,58 |
0,4429 |
1,99 |
0,4767 |
2,78 |
0,4973 |
| 1,18 |
0,3810 |
1,59 |
0,4441 |
2,00 |
0,4772 |
2,80 |
0,4974 |
| 1,19 |
0,3830 |
1,60 |
0,4452 |
2,02 |
0,4783 |
2,82 |
0,4976 |
| х
|
Ф (х
) |
х
|
Ф (х
) |
х
|
Ф (х
) |
х
|
Ф (х
) |
| 1,20 |
0,3849 |
1,61 |
0,4463 |
2,04 |
0,4793 |
2,84 |
0,4977 |
| 1,21 |
0,3869 |
1,62 |
0,4474 |
2,06 |
0,4803 |
2,86 |
0,4979 |
| 1,22 |
0,3883 |
1,63 |
0,4484 |
2,08 |
0,4812 |
2,88 |
0,4980 |
| 1,23 |
0,3907 |
1,64 |
0,4495 |
2,10 |
0,4821 |
2,90 |
0,4981 |
| 1,24 |
0,3925 |
1,65 |
0,4505 |
2,12 |
0,4831 |
2,92 |
0,4982 |
| 1,25 |
0,3944 |
1,66 |
0,4515 |
2,14 |
0,4838 |
2,94 |
0,4984 |
| 1,26 |
0,3962 |
1,67 |
0,4525 |
2,16 |
0,4846 |
2,96 |
0,4985 |
| 1,27 |
0,3980 |
1,68 |
0,4535 |
2,18 |
0,4854 |
2,98 |
0,4986 |
| 1,28 |
0,3997 |
1,69 |
0,4545 |
2,20 |
0,4861 |
3,00 |
0,49865 |
| 1,29 |
0,4015 |
1,70 |
0,4554 |
2,22 |
0,4868 |
3,20 |
0,49931 |
| 1,30 |
0,4032 |
1,71 |
0,4564 |
2,24 |
0,4875 |
3,40 |
0,49966 |
| 1,31 |
0,4049 |
1,72 |
0,4573 |
2,26 |
0,4881 |
3,60 |
0,499841 |
| 1,32 |
0,4066 |
1,73 |
0,4582 |
2,28 |
0,4887 |
3,80 |
0,499928 |
| 1,33 |
0,4082 |
1,74 |
0,4591 |
2,30 |
0,4893 |
4,00 |
0,499968 |
| 1,34 |
0,4099 |
1,75 |
0,4599 |
2,32 |
0,4898 |
4,50 |
0,499997 |
| 1,35 |
0,4115 |
1,16 |
0,4608 |
2,34 |
0,4904 |
5,00 |
0,499997 |
| 1,36 |
0,4131 |
1,77 |
0,4616 |
Вероятность появления русских букв в тексте без учета знаков препинания
Р(О) =0,109 Р(Е,Ё) = 0,087
Р(А) = 0,075 Р(И) = 0,075
Вероятность регистрации студента с фамилией, начинающейся с буквы К
Р = 0,143
Вероятность регистрации мальчика среди новорожденных
Р = 0,518
Вероятность выпадения цифр 1,2,3,44,5 или 6
Р=0,5
Вероятность выпадения герба
Р=0,5
Задание 2
| №
серии
|
n
i
-
число испытаний в серии
|
m
i
- число появлений события А
|
w
i
(A)
- частота появления события А
|
N
i
- число испытаний в объединённой серии
|
M
i
- число появления события А в объединённой серии
|
Wi(A)
- частота появления события А в объединённой серии
|
P(A)
|
ε = |W-P|
|
P(A)+ε
|
P(A)-ε
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| 1 |
100 |
8 |
0,080 |
200 |
8 |
0,040 |
0,075 |
0,010 |
0,085 |
0,065 |
| 2 |
100 |
10 |
0,100 |
46 |
18 |
0,391 |
0,075 |
0,010 |
0,085 |
0,065 |
| 3 |
100 |
6 |
0,060 |
246 |
24 |
0,098 |
0,075 |
0,010 |
0,085 |
0,065 |
| 4 |
100 |
9 |
0,090 |
346 |
33 |
0,095 |
0,075 |
0,010 |
0,085 |
0,065 |
| 5 |
100 |
10 |
0,100 |
446 |
43 |
0,096 |
0,075 |
0,010 |
0,085 |
0,065 |
| 6 |
100 |
15 |
0,150 |
546 |
58 |
0,106 |
0,075 |
0,010 |
0,085 |
0,065 |
| 7 |
100 |
6 |
0,060 |
646 |
64 |
0,099 |
0,075 |
0,010 |
0,085 |
0,065 |
| 8 |
100 |
9 |
0,090 |
746 |
73 |
0,098 |
0,075 |
0,010 |
0,085 |
0,065 |
| 9 |
100 |
6 |
0,060 |
846 |
79 |
0,093 |
0,075 |
0,010 |
0,085 |
0,065 |
| 10 |
100 |
2 |
0,020 |
946 |
81 |
0,086 |
0,075 |
0,010 |
0,085 |
0,065 |
| 11 |
100 |
5 |
0,050 |
1046 |
86 |
0,082 |
0,075 |
0,010 |
0,085 |
0,065 |
| 12 |
100 |
1 |
0,010 |
1146 |
87 |
0,076 |
0,075 |
0,010 |
0,085 |
0,065 |
| 13 |
100 |
3 |
0,030 |
1246 |
90 |
0,072 |
0,075 |
0,010 |
0,085 |
0,065 |
| 14 |
100 |
5 |
0,050 |
1346 |
95 |
0,071 |
0,075 |
0,010 |
0,085 |
0,065 |
| 15 |
100 |
8 |
0,080 |
1446 |
103 |
0,071 |
0,075 |
0,010 |
0,085 |
0,065 |
| 16 |
100 |
6 |
0,060 |
1546 |
109 |
0,071 |
0,075 |
0,010 |
0,085 |
0,065 |
| 17 |
100 |
5 |
0,050 |
1646 |
114 |
0,069 |
0,075 |
0,010 |
0,085 |
0,065 |
| 18 |
100 |
7 |
0,070 |
1746 |
121 |
0,069 |
0,075 |
0,010 |
0,085 |
0,065 |
| 19 |
100 |
4 |
0,040 |
1846 |
125 |
0,068 |
0,075 |
0,010 |
0,085 |
0,065 |
| 20 |
100 |
2 |
0,020 |
1946 |
127 |
0,065 |
0,075 |
0,010 |
0,085 |
0,065 |
| Выпадение герба при бросании монеты. |
| № 1-100 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
| № 101-200 |
| 1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
| № 201-300 |
| 1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
| 0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
| № 301-400 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
| № 401-500 |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
| № 501-600 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
| № 601-700 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| № 701-800 |
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
| Регистрация новорожденных мальчиков |
| № 1-120 |
| 1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
| 1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
| № 121-240 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
| № 241-360 |
| 1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
| № 361-480 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
| 1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| № 481-600 |
| 0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| № 601-720 |
| 0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
| 0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
| № 721-840 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
| № 841-960 |
| 1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
| 1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| № 961-1080 |
| 1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 3. Распределение фамилий, начинающихся с буквы К, в группах |
| группа |
Количество студентов |
количество фамилий, начинающихся с буквы К |
группа |
количество
студентов
|
количество фамилий, начинающихся с буквы К |
| С 01 |
19 |
2 |
Д91 |
23 |
4 |
| С 02 |
20 |
2 |
Д92 |
25 |
3 |
| С 03 |
17 |
1 |
Д93 |
24 |
3 |
| С 04 |
16 |
3 |
Д94 |
25 |
5 |
| Э 01 |
21 |
3 |
Л91 |
25 |
2 |
| Э 02 |
24 |
3 |
Л92 |
25 |
4 |
| А 01 |
26 |
2 |
Р91 |
25 |
2 |
| Д 01 |
22 |
5 |
Р92 |
24 |
4 |
| Д 02 |
20 |
0 |
Р93 |
24 |
4 |
| Д 03 |
19 |
6 |
К91 |
24 |
4 |
| Д 04 |
20 |
3 |
К92 |
23 |
2 |
| Д 05 |
20 |
5 |
Т91 |
23 |
8 |
| Л 01 |
24 |
4 |
Т92 |
25 |
2 |
| Л 02 |
29 |
0 |
Т93 |
24 |
2 |
| Р 01 |
26 |
3 |
Т94 |
23 |
2 |
| Р 02 |
25 |
5 |
Т95 |
23 |
4 |
| Р 03 |
25 |
1 |
Т96 |
25 |
3 |
| К 01 |
25 |
2 |
С82 |
23 |
5 |
| К 02 |
25 |
4 |
С83 |
23 |
4 |
| Т 01 |
25 |
4 |
Э81 |
24 |
5 |
| Т 02 |
25 |
4 |
Э82 |
20 |
2 |
| ТО3 |
25 |
3 |
А81 |
20 |
2 |
| ТО4 |
25 |
5 |
А82 |
22 |
1 |
| ТО5 |
25 |
5 |
Д81 |
25 |
4 |
| ТО6 |
25 |
2 |
Д82 |
22 |
1 |
| С91 |
23 |
4 |
Д83 |
25 |
4 |
| С92 |
22 |
7 |
Д84 |
25 |
3 |
| Э92 |
23 |
4 |
Л81 |
25 |
4 |
| З92 |
27 |
2 |
Л82 |
21 |
1 |
| А91 |
23 |
2 |
Р81 |
24 |
2 |
| А92 |
25 |
3 |
Р82 |
22 |
2 |
| Д91 |
23 |
4 |
Р83 |
21 |
2 |
| Выпадение цифр при бросании игральной кости |
| № 1-150 |
| 2 |
6 |
2 |
2 |
4 |
6 |
1 |
6 |
3 |
3 |
6 |
1 |
5 |
2 |
3 |
2 |
5 |
6 |
2 |
3 |
3 |
4 |
4 |
2 |
2 |
| 2 |
6 |
2 |
5 |
2 |
6 |
5 |
5 |
6 |
3 |
2 |
3 |
1 |
6 |
5 |
3 |
3 |
6 |
6 |
5 |
3 |
1 |
5 |
6 |
4 |
| 1 |
4 |
1 |
5 |
1 |
2 |
2 |
2 |
6 |
6 |
4 |
5 |
3 |
4 |
3 |
3 |
2 |
3 |
4 |
5 |
5 |
5 |
2 |
1 |
6 |
| 2 |
1 |
5 |
4 |
5 |
6 |
4 |
5 |
6 |
2 |
3 |
5 |
2 |
2 |
2 |
6 |
3 |
1 |
5 |
5 |
3 |
2 |
5 |
1 |
4 |
| 2 |
3 |
5 |
6 |
2 |
3 |
3 |
3 |
1 |
5 |
4 |
2 |
2 |
3 |
5 |
4 |
4 |
5 |
6 |
5 |
3 |
4 |
1 |
1 |
2 |
| 3 |
3 |
5 |
2 |
3 |
3 |
3 |
2 |
6 |
3 |
5 |
3 |
4 |
4 |
5 |
5 |
3 |
5 |
1 |
2 |
6 |
2 |
4 |
1 |
2 |
| № 151-300 |
| 5 |
6 |
5 |
2 |
4 |
2 |
3 |
6 |
4 |
2 |
2 |
6 |
5 |
4 |
1 |
2 |
1 |
6 |
2 |
5 |
1 |
1 |
1 |
4 |
2 |
| 4 |
4 |
3 |
4 |
1 |
5 |
3 |
3 |
6 |
2 |
5 |
5 |
3 |
1 |
3 |
4 |
1 |
5 |
3 |
2 |
6 |
6 |
3 |
5 |
3 |
| 4 |
3 |
1 |
2 |
2 |
4 |
2 |
3 |
5 |
2 |
5 |
4 |
6 |
4 |
6 |
3 |
6 |
4 |
4 |
2 |
1 |
1 |
2 |
5 |
4 |
| 3 |
3 |
5 |
2 |
3 |
3 |
3 |
2 |
6 |
3 |
5 |
3 |
4 |
4 |
5 |
5 |
3 |
5 |
1 |
2 |
6 |
2 |
4 |
1 |
3 |
| 1 |
1 |
2 |
6 |
2 |
1 |
4 |
5 |
3 |
6 |
2 |
4 |
6 |
1 |
2 |
6 |
3 |
6 |
6 |
6 |
6 |
2 |
1 |
5 |
5 |
| 3 |
3 |
5 |
3 |
2 |
4 |
1 |
6 |
2 |
3 |
4 |
2 |
4 |
3 |
4 |
4 |
6 |
5 |
4 |
4 |
6 |
2 |
6 |
1 |
2 |
| № 301-450 |
| 4 |
5 |
4 |
1 |
2 |
4 |
5 |
3 |
5 |
3 |
2 |
3 |
6 |
2 |
1 |
2 |
5 |
3 |
5 |
6 |
4 |
6 |
1 |
6 |
1 |
| 6 |
2 |
3 |
2 |
4 |
2 |
5 |
4 |
5 |
6 |
6 |
4 |
5 |
5 |
2 |
1 |
6 |
3 |
1 |
3 |
1 |
4 |
5 |
5 |
4 |
| 5 |
4 |
1 |
2 |
1 |
3 |
5 |
6 |
1 |
3 |
4 |
1 |
5 |
5 |
1 |
3 |
5 |
4 |
5 |
6 |
5 |
6 |
6 |
5 |
6 |
| 5 |
3 |
5 |
3 |
4 |
3 |
1 |
2 |
1 |
6 |
3 |
3 |
6 |
5 |
4 |
6 |
6 |
3 |
4 |
2 |
4 |
2 |
3 |
1 |
6 |
| 1 |
6 |
5 |
6 |
5 |
6 |
6 |
3 |
5 |
4 |
2 |
2 |
3 |
2 |
2 |
4 |
5 |
3 |
6 |
2 |
1 |
5 |
1 |
1 |
3 |
| 2 |
3 |
1 |
5 |
6 |
5 |
6 |
6 |
1 |
4 |
6 |
2 |
3 |
1 |
5 |
5 |
6 |
6 |
1 |
2 |
4 |
5 |
6 |
3 |
5 |
| № 451-600 |
| 6 |
2 |
4 |
6 |
6 |
4 |
4 |
2 |
4 |
4 |
6 |
4 |
6 |
4 |
1 |
4 |
1 |
5 |
2 |
2 |
1 |
2 |
4 |
4 |
6 |
| 1 |
1 |
5 |
4 |
4 |
1 |
4 |
5 |
3 |
6 |
4 |
4 |
3 |
5 |
2 |
2 |
1 |
1 |
1 |
4 |
3 |
5 |
5 |
6 |
2 |
| 1 |
4 |
3 |
2 |
5 |
6 |
5 |
2 |
1 |
4 |
4 |
3 |
5 |
5 |
2 |
2 |
4 |
3 |
5 |
1 |
3 |
2 |
5 |
6 |
2 |
| 3 |
6 |
1 |
3 |
5 |
4 |
4 |
2 |
6 |
5 |
5 |
4 |
3 |
2 |
4 |
5 |
6 |
6 |
2 |
6 |
4 |
4 |
1 |
5 |
2 |
| 5 |
1 |
1 |
4 |
1 |
1 |
6 |
4 |
6 |
2 |
5 |
4 |
3 |
5 |
1 |
2 |
5 |
6 |
6 |
6 |
4 |
1 |
5 |
5 |
3 |
| 2 |
1 |
1 |
1 |
5 |
3 |
5 |
2 |
5 |
6 |
4 |
2 |
5 |
2 |
1 |
1 |
3 |
5 |
6 |
5 |
4 |
6 |
4 |
3 |
2 |
| № 601-750 |
| 3 |
4 |
6 |
1 |
6 |
6 |
1 |
1 |
5 |
4 |
2 |
6 |
4 |
3 |
5 |
5 |
6 |
1 |
2 |
5 |
4 |
3 |
1 |
6 |
5 |
| 6 |
2 |
6 |
5 |
5 |
5 |
4 |
4 |
2 |
2 |
3 |
2 |
2 |
6 |
2 |
6 |
3 |
2 |
6 |
5 |
1 |
5 |
3 |
6 |
4 |
| 1 |
5 |
6 |
1 |
6 |
2 |
1 |
3 |
5 |
5 |
6 |
3 |
6 |
5 |
2 |
5 |
1 |
2 |
1 |
2 |
4 |
6 |
3 |
1 |
4 |
| 5 |
2 |
6 |
6 |
2 |
4 |
2 |
6 |
2 |
1 |
5 |
1 |
5 |
6 |
4 |
2 |
3 |
6 |
5 |
5 |
1 |
5 |
6 |
6 |
6 |
| 4 |
2 |
5 |
4 |
1 |
4 |
2 |
2 |
6 |
4 |
3 |
3 |
5 |
1 |
3 |
6 |
5 |
3 |
1 |
3 |
3 |
4 |
5 |
5 |
6 |
| 6 |
2 |
3 |
1 |
1 |
3 |
3 |
1 |
6 |
3 |
6 |
5 |
2 |
5 |
1 |
5 |
1 |
4 |
3 |
2 |
4 |
4 |
6 |
5 |
6 |
| № 751-900 |
| 3 |
1 |
2 |
4 |
1 |
6 |
2 |
3 |
5 |
4 |
6 |
4 |
3 |
6 |
1 |
3 |
4 |
6 |
3 |
1 |
6 |
1 |
1 |
6 |
1 |
| 4 |
4 |
1 |
3 |
6 |
1 |
3 |
3 |
4 |
1 |
5 |
2 |
1 |
2 |
1 |
3 |
5 |
1 |
5 |
5 |
5 |
6 |
6 |
4 |
1 |
| 2 |
5 |
2 |
6 |
2 |
3 |
5 |
2 |
6 |
2 |
5 |
5 |
5 |
4 |
6 |
6 |
6 |
1 |
3 |
3 |
3 |
3 |
2 |
1 |
1 |
| 6 |
4 |
5 |
4 |
4 |
2 |
2 |
1 |
4 |
6 |
2 |
6 |
5 |
3 |
5 |
5 |
6 |
1 |
2 |
6 |
2 |
1 |
5 |
1 |
6 |
| 4 |
5 |
3 |
5 |
3 |
1 |
2 |
2 |
1 |
4 |
4 |
4 |
2 |
1 |
6 |
3 |
6 |
2 |
1 |
1 |
5 |
3 |
4 |
1 |
3 |
| 3 |
1 |
5 |
6 |
3 |
1 |
6 |
5 |
5 |
1 |
4 |
4 |
2 |
1 |
5 |
1 |
2 |
3 |
3 |
4 |
1 |
5 |
2 |
3 |
6 |
| № 901-1051 |
| 4 |
5 |
2 |
4 |
5 |
4 |
2 |
5 |
1 |
5 |
1 |
1 |
1 |
5 |
4 |
3 |
4 |
3 |
2 |
4 |
6 |
5 |
4 |
6 |
5 |
| 2 |
6 |
4 |
2 |
2 |
4 |
2 |
3 |
3 |
6 |
5 |
1 |
2 |
4 |
3 |
5 |
4 |
3 |
4 |
2 |
5 |
4 |
1 |
4 |
4 |
| 5 |
5 |
1 |
5 |
4 |
6 |
3 |
6 |
5 |
3 |
1 |
3 |
3 |
1 |
5 |
5 |
6 |
4 |
3 |
1 |
2 |
3 |
5 |
5 |
2 |
| 4 |
6 |
5 |
4 |
1 |
1 |
4 |
6 |
2 |
6 |
5 |
5 |
3 |
3 |
4 |
2 |
3 |
4 |
6 |
2 |
3 |
4 |
5 |
4 |
5 |
| 1 |
5 |
4 |
1 |
4 |
5 |
2 |
6 |
6 |
1 |
6 |
1 |
3 |
5 |
6 |
3 |
1 |
5 |
5 |
3 |
4 |
5 |
6 |
5 |
4 |
| 3 |
2 |
3 |
6 |
4 |
5 |
4 |
5 |
3 |
6 |
2 |
5 |
4 |
4 |
5 |
6 |
2 |
1 |
2 |
3 |
4 |
5 |
4 |
3 |
1 |
|