Министерство науки и образования Украины
Национальный технический университет Украины
"Киевский политехнический институт"
Радиотехнический факультет
Контрольная работа
По курсу: "Основы научных исследований"
Тема: "Методика регрессионного анализа"
Киев 2007
Нахождение коэффициентов регрессии модели полнофакторного эксперимента типа 23
Факторный эксперимент связан с варьированием одновременно всех факторов и проверкой достоверности результатов математико-статистическими методами. Факторы в эксперименте можно варьировать на бесконечном множестве уровней. При планировании эксперимента, чтобы получить результаты эксперимента в виде удобных для анализа полиномов, достаточно изменять факторы на двух, трех или пяти уровнях. Проведение экспериментов с многоуровневыми факторами затруднительно, поэтому они находят ограниченное применение в практике инженерного эксперимента.
Таблица 1
Номер
комбинации
|
Факторы |
Произведения факторов |
Параметры оптимизации
(экспертная оценка)
|
Параметр
оптимизации
|
| _ |
Ф |
И |
С |
| x0 |
x1 |
x2 |
x3 |
x1x2 |
x1x3 |
x2x3 |
x1x2x3 |
y1 |
y2 |
y3 |
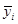 |
| 1 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
| 2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
31 |
28 |
47 |
35,3 |
| 3 |
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
12 |
9 |
10 |
10,3 |
| 4 |
1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
60 |
52 |
64 |
58,7 |
| 5 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
3 |
2 |
2 |
| 6 |
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
54 |
59 |
50 |
54,3 |
| 7 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
41 |
41 |
40 |
40,7 |
| 8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
91 |
92 |
90 |
91 |
| Среднее значение |
24,8 |
Модель для ПФЭ типа 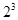 выглядит следующим образом: выглядит следующим образом:
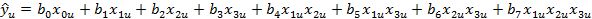
Коэффициенты уравнения регрессии по методу наименьших квадратов в матричной форме определяем следующим образом [1, с. 53-55]:
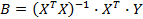
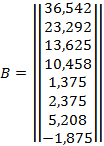
Выражение 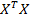 - квадратная симметричная матрица – называется матрицей системы нормальных уравнений, или информационной матрицей (матрицей Фишера); - квадратная симметричная матрица – называется матрицей системы нормальных уравнений, или информационной матрицей (матрицей Фишера); 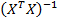 – ковариационная матрица, или матрица дисперсий ковариаций. – ковариационная матрица, или матрица дисперсий ковариаций.
Ковариация показывает величину статистической взаимосвязи между эффектами модели xi
и xj
:
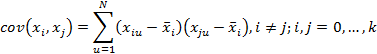
Также коэффициенты ковариаций можно определить из ковариационной матрицы:
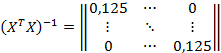
Из матрицы видно, что коэффициенты ковариаций каждого эффекта с каждым равны нулю, отсюда делаем вывод, что коэффициенты уравнения регрессии не коррелированны между собой.
Проверка многофакторных статистических моделей по основными критериям качества
Проверка на статистическую значимость получаемой математической модели [1, с. 93-94]
Проводиться проверка статистической гипотезы о силе влияния факторов плана эксперимента на фоне случайной изменчивости повторных опытов:
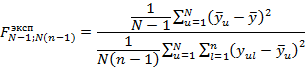
Где 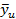 – среднее значения результатов опытов в u
-той строке матрицы результатов; – среднее значения результатов опытов в u
-той строке матрицы результатов; 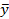 – среднее значение по всем результатам опытов; – среднее значение по всем результатам опытов; 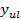 - результат в u
-той строке l
-го повторного опыта; - результат в u
-той строке l
-го повторного опыта; 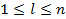 (n – количество повторных опытов (2)) (n – количество повторных опытов (2))
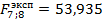
По таблице (приложение 3) определяем 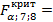 3,73 3,73
Поскольку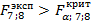 (53,935>3,73), то делаем положительный вывод о целесообразности получения математической модели. (53,935>3,73), то делаем положительный вывод о целесообразности получения математической модели.
Проверки предпосылок о свойствах случайных ошибок входящие в результаты экспериментов [1, с. 93]
При равномерном дублировании опытов nu
= n = const (в нашем случае n = 2). Проверка однородностиряда дисперсий производиться с использованием G
-критерия Кохрена:
Реклама

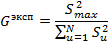
- вычисляется по формуле:
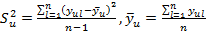
Число степеней свободы, которыми обладает каждая из дисперсий: n – 1 = 1;
Количество независимых оценок дисперсий: N = 8
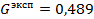
По указанным индексам находим значение 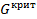 из таблицы "Критерий Кохрена" (приложение 1) из таблицы "Критерий Кохрена" (приложение 1)
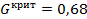
Так как 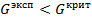 то делаем вывод, что дисперсии однородны и могут быть усреднены: то делаем вывод, что дисперсии однородны и могут быть усреднены:
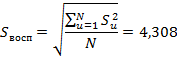
Проверка на адекватность полученной модели произвольным результатам экспериментов в пределах принятых изменений факторов [1, с. 94-95]
Проверка коэффициентов уравнения регрессии на статистическую значимость проводиться с помощью t
-критерия:
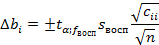
Для значения α = 0,05, получим α/2 = 0,025 и 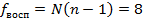 значение t-критерия Стьюдента равно значение t-критерия Стьюдента равно 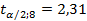 . Поскольку в матрице дисперсий-ковариаций не нулевые только диагональные элементы и равны между собой ( . Поскольку в матрице дисперсий-ковариаций не нулевые только диагональные элементы и равны между собой ( ), то все доверительные интервалы равны между собой: ), то все доверительные интервалы равны между собой:
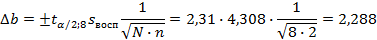
Теперь проверим все коэффициенты на статистическую значимость исходя из условия: если 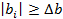 – то коэффициент статистически значим, если – то коэффициент статистически значим, если 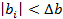 – то коэффициент статистически не значим. – то коэффициент статистически не значим.
| коэффициент |
b0
|
b1
|
b2
|
b3
|
b4
|
b5
|
b6
|
b7
|
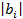 |
36,542 |
23,292 |
13,625 |
10,458 |
1,375 |
2,375 |
5,208 |
1,875 |
| Статистически значим |
+ |
+ |
+ |
+ |
- |
+ |
+ |
- |
Таким образом мы получили, что коэффициенты b
4
и b
7
– статически не значимы, поэтому мы не будем вносить их в нашу модель. И окончательный вид модели будет таким:
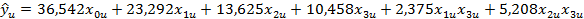
Число 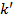 = 6 – количество эффектов, которые вошли в структуру модели, то есть статистически значимые. = 6 – количество эффектов, которые вошли в структуру модели, то есть статистически значимые.
Значения откликов, полученных с помощью последней модели:
| Отклик |
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
y8
|
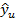 |
-3.25 |
38.584 |
13.584 |
55.418 |
2.5 |
53.834 |
40.166 |
91.5 |
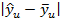 |
3.25 |
3.251 |
3.251 |
3.249 |
0.5 |
0.499 |
0.501 |
0.5 |
Проверка модели на адекватность производиться с использованием F
-критерия Фишера:
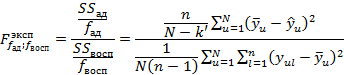
Где 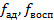 – числа степеней свободы для – числа степеней свободы для 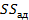 и и 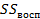 : :

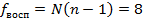
Просчитаем экспериментальное значение:
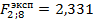
По таблицам значения критерия Фишера (приложения 3) для q = 0,05 находим:
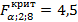
Так как выполняется условие 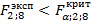 значит модель адекватна. значит модель адекватна.
Так как у нас 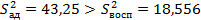 , то нет необходимости определять значимость обратного отношения дисперсий. , то нет необходимости определять значимость обратного отношения дисперсий.
Проверка на информативность [1, с. 97-99]
Коэффициент множественной корреляции R
определяется по формуле:
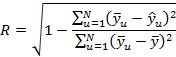
Посчитанное значение R = 0,997 которое очень близко к единице.
Гипотезу о значимости множественного коэффициента корреляции проверяют по F
-критерию:
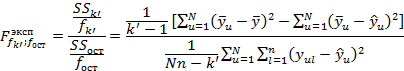
Где 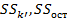 – суммы квадратов отклонений – связанная с – суммы квадратов отклонений – связанная с 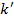 коэффициентом модели и остаточная; коэффициентом модели и остаточная; 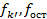 – числа степеней свободы для – числа степеней свободы для 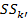 и и 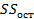 . .
В нашем случае:
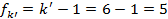
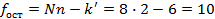
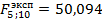
По таблицам значения критерия Фишера для q = 0,05 находим:

Поскольку 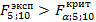 , то гипотеза о статистической незначимости R
не принимается – это значит, что коэффициент множественной корреляции R
является статистически значимым. , то гипотеза о статистической незначимости R
не принимается – это значит, что коэффициент множественной корреляции R
является статистически значимым.
Проверка на устойчивость коэффициентов математической модели к случайным составляющим в исходной информации [1, с. 99-101]
Коэффициенты математической модели должны быть устойчивы к малым случайным изменениям в исходных данных, полученных в процессе эксперимента. Для количественно показателя устойчивости коэффициентов математической модели будем использовать меру обусловленности матрицы по Нейману-Голдстейну.
Реклама

Для определения меры обусловленности по Нейману-Голдстейну P
необходимо найти собственные числа для матрицы Фишера 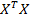 , решая уравнение: , решая уравнение:
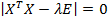
Где 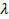 – собственные числа для информационной матрицы Фишера – собственные числа для информационной матрицы Фишера 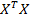
Поскольку коэффициенты b
4
и b
7
статистически незначимы, тога соответствующие столбцы матрицы X
отбрасываются и размер матрицы становится  , размер обратной матрицы - , размер обратной матрицы - 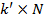 , а размер матрицы Фишера - , а размер матрицы Фишера - 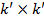 : :

Так как все эффекты в матрице Фишера ортогональны друг другу и нормированы, то:
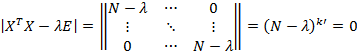
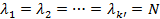
Находят 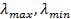 – максимальное и минимальное собственное число для информационной матрицы Фишера – максимальное и минимальное собственное число для информационной матрицы Фишера 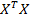 : :
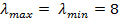
Мера обусловленности по Нейману-Голдстейну:
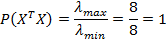
Другая мера обусловленности матрицы 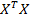 обозначается латинским сокращением cond
: обозначается латинским сокращением cond
:
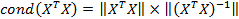
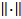 - обозначение нормы матрицы. При этом предполагается, что матрица - обозначение нормы матрицы. При этом предполагается, что матрица 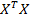 невырождена. невырождена.
Известны несколько видов норм для матрицы А
. Каждой из векторных норм соответствует своя подчиненная норма матрицы. Будем использовать следующую форму:
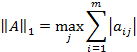
что означает выбор по всем столбцам j
максимальной суммы абсолютных значений элементов по строкам i
(m
– число строк матрицы А
).
Так как все эффекты в расширенной матрице X
ортогональны друг другу, то:
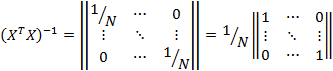
Для матрицы 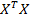 каждая по столбцам каждая по столбцам 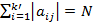 . Для матрицы . Для матрицы 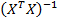 каждая по столбцам каждая по столбцам 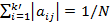 . .
Число обусловленности в этом случае будет:
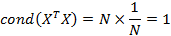
Что подтверждает результат, полученный предыдущим методом.
Проверка фактической эффективности извлечения полезной информации из исходных данных [1, с. 101-102]
Косвенным показателем эффективности может быть число обусловленности cond
для полученной модели. Так как 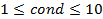 значит эффективность можно считать хорошей. значит эффективность можно считать хорошей.
Проверка правильности описания полученной математической модели по всей области моделирования [1, с. 102]
Полученную математическую модель желательно проверить по контрольной выборке. С использованием ПС ПРИАМ можно построить трехмерное изображение поверхности отклика, и проанализировать полученную поверхность, сравнивая минимальные и максимальные расчетные значения 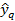 с допустимыми физическими значениями отклика. Возможен также поиск минимума и максимума по модели с допустимыми физическими значениями отклика. Возможен также поиск минимума и максимума по модели 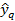 с использованием ЛПτ равномерно распределенных последовательностей и сравнения с физически возможными значениями отклика. с использованием ЛПτ равномерно распределенных последовательностей и сравнения с физически возможными значениями отклика.
Оценка семантичности по полученным коэффициентам математической модели [1, с. 102-103]
Семантичность достигается, если эффекты статистической модели ортогональны друг другу, нормированы и план эксперимента равномерный. Выбор структуры модели должен быть проведен с использованием алгоритма RASTA3 и ПС ПРИАМ.
В нашем случае все эффекты полученной модели ортогональны друг другу и нормированы, план эксперимента мы выбрали равномерный, следовательно семантичность достигается.
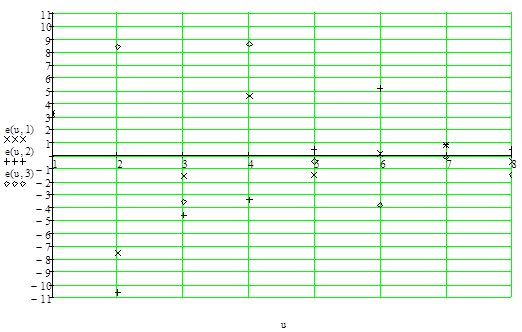
Проверка свойств остатков [1, с. 103, 364-366]
Анализ основных графиков остатков 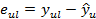
Общая оценка свойств полученной математической модели и возможностей ее использования для достижения поставленной цени
Из вышеприведенных расчетов и проверок можно сделать вывод, что данная математическая модель является адекватной для ее использования в поставленных задачах.
Литература
1. Рядченко С.Г. Устойчивые методы оценивания статистических моделей. Монография. – К.: ПП "Санспарель", 2005. – 504 с.
2. Большов Л.Н., Смирнов Н.В. Таблицы математической статистики
Приложения
1. Значение критерия Кохрена G1-
q
для q = 0,05. Все значения G1-
q
меньше единицы, поэтому в таблице приведены лишь знаки, следующие после запятой.
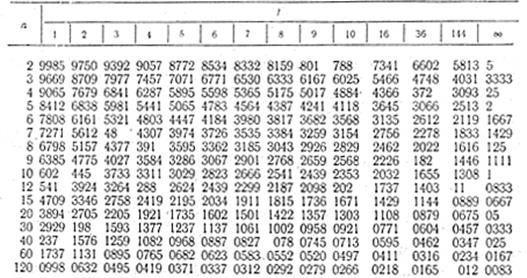
2. Значения критерия Стьюдента (t
- критерия)
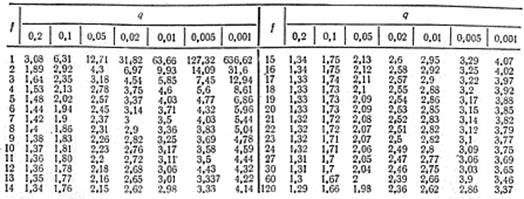
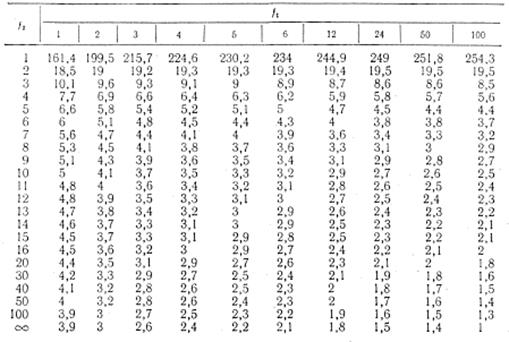
3. Значения критерия Фишера F1-
q
для q = 0,05
|