Оглавление
ВВЕДЕНИЕ 3
1. КРАТКИЙ ОБЗОР АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧ ДАННОГО ТИПА 5
1.1 Математическое программирование 5
1.2 Табличный симплекс - метод 6
1.3 Метод искусственного базиса 7
1.4 Модифицированный симплекс - метод 7
2.СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ 9
3.РАЗРАБОТКА И ОПИСАНИЕ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ 10
3.1 Построение математической модели задачи 10
3.2 Решение задачи вручную 11
4.НАЗНАЧЕНИЕ ПРОГРАММЫ 14
5.ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЮ 15
6. ТЕКСТ ИСХОДНОГО МОДУЛЯ 17
Заключение 29
Список использованных источников 30
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была "повинна" математика, развивающаяся на протяжении нескольких веков в основном в связи с потребностями физики и техники. Но главные причины лежат все же в природе экономических процессов, в специфике экономической науки.
Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием сложная система.
Наиболее распространено понимание системы как совокупности элементов, находящихся во взаимодействии и образующих некоторую целостность, единство. Важным качеством любой системы является эмерджентность - наличие таких свойств, которые не присущи ни одному из элементов, входящих в систему. Поэтому при изучении систем недостаточно пользоваться методом их расчленения на элементы с последующим изучением этих элементов в отдельности. Одна из трудностей экономических исследований - в том, что почти не существует экономических объектов, которые можно было бы рассматривать как отдельные (внесистемные) элементы.
Сложность системы определяется количеством входящих в нее элементов, связями между этими элементами, а также взаимоотношениями между системой и средой. Экономика страны обладает всеми признаками очень сложной системы. Она объединяет огромное число элементов, отличается многообразием внутренних связей и связей с другими системами (природная среда, экономика других стран и т.д.). В народном хозяйстве взаимодействуют природные, технологические, социальные процессы, объективные и субъективные факторы.
Сложность экономики иногда рассматривалась как обоснование невозможности ее моделирования, изучения средствами математики. Но такая точка зрения в принципе неверна. Моделировать можно объект любой природы и любой сложности. И как раз сложные объекты представляют наибольший интерес для моделирования; именно здесь моделирование может дать результаты, которые нельзя получить другими способами исследования.
Реклама

Потенциальная возможность математического моделирования любых экономических объектов и процессов не означает, разумеется, ее успешной осуществимости при данном уровне экономических и математических знаний, имеющейся конкретной информации и вычислительной технике. И хотя нельзя указать абсолютные границы математической формализуемости экономических проблем, всегда будут существовать еще неформализованные проблемы, а также ситуации, где математическое моделирование недостаточно эффективно.
1. КРАТКИЙ ОБЗОР АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧ ДАННОГО ТИПА 1.1 Математическое программирование
Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом : найти экстремум некоторой функции многих переменных f ( x1, x2, ... , xn ) при ограничениях gi ( x1, x2, ... , xn ) * bi , где gi - функция, описывающая ограничения, * - один из следующих знаков Ј , = , і , а bi - действительное число, i = 1, ... , m. f называется функцией цели ( целевая функция ).
Линейное программирование - это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.
Задачу линейного программирования можно сформулировать так . Найти max
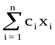
при условии : a11 x1 + a12 x2 + . . . + a1n xn Ј b1 ;
a21 x1 + a22 x2 + . . . + a2n xn Ј b2 ;
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 + am2 x2 + . . . + amn xn Ј bm ;
x1 і 0, x2 і 0, . . . , xn і 0 .
Эти ограничения называются условиями неотрицательности. Если все ограничения заданы в виде строгих равенств, то данная форма называется канонической.
В матричной форме задачу линейного программирования записывают следующим образом. Найти max cT x
при условии
A x Ј b ;
x і 0 ,
где А - матрица ограничений размером ( mґn), b(mґ1) - вектор-столбец свободных членов, x(n ґ 1) - вектор переменных, сТ = [c1, c2, ... , cn ] - вектор-строка коэффициентов целевой функции.
Реклама

Решение х0 называется оптимальным, если для него выполняется условие сТ х0 і сТ х , для всех х О R(x).
Поскольку min f(x) эквивалентен max [ - f(x) ] , то задачу линейного программирования всегда можно свести к эквивалентной задаче максимизации.
Для решения задач данного типа применяются методы:
1) графический;
2) табличный ( прямой, простой ) симплекс - метод;
3) метод искусственного базиса;
4) модифицированный симплекс - метод;
5) двойственный симплекс - метод.
1.2 Табличный симплекс - метод
Для его применения необходимо, чтобы знаки в ограничениях были вида “ меньше либо равно ”, а компоненты вектора b - положительны.
Алгоритм решения сводится к следующему :
Приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам.
Если в исходной системе ограничений присутствовали знаки “ равно ” или “ больше либо равно ”, то в указанные ограничения добавляются
искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума.
Формируется симплекс-таблица.
Рассчитываются симплекс-разности.
Принимается решение об окончании либо продолжении счёта.
При необходимости выполняются итерации.
На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу Жордана-Гаусса или каким-нибудь другим способом.
1.3 Метод искусственного базиса
Данный метод решения применяется при наличии в ограничении знаков “ равно ”, “ больше либо равно ”, “ меньше либо равно ” и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами m , а в задачи минимизации - с положительными m . Таким образом из исходной получается новая m - задача.
Если в оптимальном решении m - задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении m - задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.
1.4 Модифицированный симплекс - метод
В основу данной разновидности симплекс-метода положены такие особенности линейной алгебры , которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы.
В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущим базисным векторам. Указанная способность делает весьма привлекательной машинную реализацию вычислений вследствие экономии памяти под промежуточные переменные и значительного сокращения времени счёта. Хорош для ситуаций, когда число переменных n значительно превышает число ограничений m.
В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности, принятие решений о коррекции базиса и исключение Жордана-Гаусса.
Особенности заключаются в наличии двух таблиц - основной и вспомагательной, порядке их заполнения и некоторой специфичности расчётных формул.
2.СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ
Для производства двух видов изделий А и В используется три типа технологического оборудования. На производство единицы изделия А идёт времени, часов : оборудованием 1-го типа - а1 , оборудованием 2-го типа - а2 , оборудованием 3-го типа - а3 . На производство единицы изделия В идёт времени, часов : оборудованием 1-го типа - b1 , оборудованием 2-го типа - b2 ,, оборудованием 3-го типа - b3 .
На изготовление всех изделий администрация предприятия может предоставить оборудование 1-го типа не более, чем на t1 , оборудование 2-го типа не более, чем на t2 , оборудование 3-го типа не более, чем на t3 часов.
Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами.
а1 = 1 b1 = 5 t1 = 10 a = 2
а2 = 3 b2 = 2 t2 = 12 b = 3
а3 = 2 b3 = 4 t3 = 10
3.РАЗРАБОТКА И ОПИСАНИЕ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ 3.1 Построение математической модели задачи
| На произв-во изделия А, часов |
На произв-во изделия B, часов |
Предпр-е предоставит, часов |
| Оборуд-е 1го типа |
1 |
5 |
10 |
| Оборуд-е 2го типа |
3 |
2 |
12 |
| Оборуд-е 3го типа |
2 |
4 |
10 |
| Прибыль от реализации, за ед. изд-я |
2 |
3 |
Построение математической модели осуществляется в три этапа :
1. Определение переменных, для которых будет составляться математическая модель.
Так как требуется определить план производства изделий А и В, то переменными модели будут:
x1 - объём производства изделия А, в единицах;
x2 - объём производства изделия В, в единицах.
2. Формирование целевой функции.
Так как прибыль от реализации единицы готовых изделий А и В известна, то общий доход от их реализации составляет 2x1 + 3x2 ( рублей ). Обозначив общий доход через F, можно дать следующую математическую формулировку целевой функции : определить допустимые значения переменных x1 и x2 , максимизирующих целевую функцию F = 2x1 + 3x2 .
3. Формирование системы ограничений.
При определении плана производства продукции должны быть учтены ограничения на время, которое администрация предприятия сможет предоставить на изготовления всех изделий. Это приводит к следующим трём ограничениям :
x1 + 5x2 Ј 10 ; 3x1 + 2x2 Ј 12 ; 2x1 + 4x2 Ј 10 .
Так как объёмы производства продукции не могут принимать отрицательные значения, то появляются ограничения неотрицательности :
x1 і 0 ; x2 і 0 .
Таким образом, математическая модель задачи представлена в виде : определить план x1 , x2 , обеспечивающий максимальное значение функции :
max F = max ( 2x1 + 3x2 )
при наличии ограничений :
x1 + 5x2 Ј 10 ;
3x1 + 2x2 Ј 12 ;
2x1 + 4x2 Ј 10 .
x1 і 0 ; x2 і 0 .
3.2 Решение задачи вручную
Табличный метод ещё называется метод последовательного улучшения оценки. Решение задачи осуществляется поэтапно.
1. Приведение задачи к форме :
x1 + 5x2 Ј 10 ;
3x1 + 2x2 Ј 12 ;
2x1 + 4x2 Ј 10 .
x1 і 0 ; x2 і 0 .
2. Канонизируем систему ограничений :
x1 + 5x2 + x3 = 10 ;
3x1 + 2x2 + x4 = 12 ;
2x1 + 4x2 + x5 = 10 .
x1 і 0 ; x2 і 0 .
A1 A2 A3 A4 A5 A0
3. Заполняется исходная симплекс-таблица и рассчитываются симплекс-разности по формулам :
d0 = 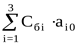 - текущее значение целевой функции - текущее значение целевой функции
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A3
|
0 |
10 |
1 |
5 |
1 |
0 |
0 |
| A4
|
0 |
12 |
3 |
2 |
0 |
1 |
0 |
| A5
|
0 |
10 |
2 |
4 |
0 |
0 |
1 |
| d |
0 |
-2 |
-3 |
0 |
0 |
0 |
di = 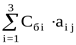 - расчёт симплекс-разностей, где j = 1..6 . - расчёт симплекс-разностей, где j = 1..6 .
Так как при решении задачи на max не все симплекс-разности положительные, то оптимальное решение можно улучшить.
4. Определяем направляющий столбец j*. Для задачи на max он определяется минимальной отрицательной симплекс-разностью. В данном случае это вектор А2
5. Вектор i*, который нужно вывести из базиса, определяется по отношению :
min 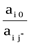 при аi j > 0 при аi j > 0
В данном случае сначала это А3 .
5. Заполняется новая симплекс-таблица по исключеню Жордана - Гаусса :
а). направляющую строку i* делим на направляющий элемент :
a i j = a i j / a i j , где j = 1..6
б). преобразование всей оставшейся части матрицы :
a ij = aij - a i j Ч aij , где i № i* , j № j*
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
2 |
1/5 |
1 |
1/5 |
0 |
0 |
| A4
|
0 |
8 |
13/5 |
0 |
-2/5 |
1 |
0 |
| A5
|
0 |
2 |
6/5 |
0 |
-4/5 |
0 |
1 |
| d |
6 |
-7/5 |
0 |
3/5 |
0 |
0 |
В результате преобразований получаем новую симплекс-таблицу :
Повторяя пункты 3 - 5, получим следующие таблицы :
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
5/3 |
0 |
1 |
1/3 |
0 |
-1/6 |
| A4
|
0 |
11/3 |
0 |
0 |
4/3 |
1 |
-13/6 |
| A1
|
2 |
5/3 |
1 |
0 |
-2/3 |
0 |
5/6 |
| d |
8 1/3 |
0 |
0 |
-1/3 |
0 |
7/6 |
| C
|
2 |
3 |
0 |
0 |
0 |
| Б
|
Cб
|
A0
|
A1
|
A2
|
A3
|
A4
|
A5
|
| A2
|
3 |
3/4 |
0 |
1 |
0 |
-1/4 |
3/8 |
| A3
|
0 |
11/4 |
0 |
0 |
1 |
3/4 |
-13/8 |
| A1
|
2 |
7/2 |
1 |
0 |
0 |
1/2 |
-1/4 |
| d |
9 1/4 |
0 |
0 |
0 |
1/4 |
5/8 |
Так как все симплекс-разности положительны, то оптимальное решение найдено :
X = ( 7/2 , 3/4 , 11/4 , 0 , 0 ) ( единиц )
max F = 9 1/4 ( рублей )
4.НАЗНАЧЕНИЕ ПРОГРАММЫ
Программа предусмотрена для решения систем линейных неравенств табличным методом, а так же для попытки оптимизации различных экономических, социальных и т. д. проблем.
Метод, описанный в программе, может применяться на государственных и частных предприятиях для улучшения эффективности производства.
Задание условий
Все условия задаются в колонке “A” первого листа(программа результат помещает в лист 2)
В третьей строке(”A3″) необходимо записать целеыую функцию на минимум или максимум(min или max после =) например:
3Ч1+2Ч2+4Ч3+2Ч4=min
В 5 строке необходимо записать количество знаков в дробной части чисел(или ничего то есть пусто или пробел(ы) )
начиная с 9 строки записываются ограничения по одной строке на каждое ограничениe. Hапример:
6Ч2+6Ч3+4Ч4=60
2Ч1+4Ч2+8Ч3+8Ч4<=80
4Ч1+4Ч2+12Ч4>=20
2Ч1+6Ч2+2Ч3+8Ч4=30
(можно выделить и занести все ограничения нашего примера в буфер и вставить в ячейку “9А”, программа автоматически разместит их в строчки, что располагаются ниже.)Содержимое последней строки ограничений(В нашем примере A13) должно быть пусто или пробел(ы) Переменные Xi по умолчанию считается не отрицательными.
Во всех, не занятых условием задачи ячейках, можно писать что угодно. После ввода условий задачи клацните по кнопке, которую вы первую занесли на лист Excel.
Получение результата
Результат работы располагается на втором листе книги.
Вначале там помещается таблица изображающая условие задачи в каноническом виде, а затем очередная итерация. Любую таблицу(начальную или после очередной итерации) можно как угодно оформить для печати и распечатать. все изменения сделанные в это время на этом листе никак не влияют на следующую итерацию. При следующей итерации второй лист полностью очищается и формируются результаты новой итерации.
Для получения новой итерации следует перейти на первый лист(он называется “Initial data” и нажать кнопку для получения следующей итерации. Если промежуточные результаты не нужны, то следует последовательно нажимать на кнопку получения новой итерации, не переходя на второй лист и перейти на него только для просмотра окончательного результата.
6. ТЕКСТ ИСХОДНОГО МОДУЛЯ
Dim Ftarget As String ’целевая функция target function
Dim MaxX As Integer ‘максимальный индех Х в целевой функции
Dim MaxLi As Boolean ‘true-max; False-min
Dim AmRest As Integer ‘ Количество строк ограничений (Amount of the restrictions)
Private Type Tmy
IndX As Integer
KoefX As Double
End Type
‘Номер очередного обрабатываемого символа в строке
Dim Icurrent As Integer
Dim BgRight As Integer ’Номер байта начала правой части ограничения, иначе 0;
‘The Number of the byte begin right part of restriction, otherwise 0;
Dim Isx As String
Dim Rez() As Tmy
Dim NumIter As Integer ‘Номер итерации. Если равен нулю, канонический вид симплекс таблицы
‘Number to iterations. If is a zero, canonical type simplex tables
Dim MiCiXiAi() As Double ‘Два первых столбца этого массива заменяют первый столбец симплексной таблицы.
‘Первый столбец, это множитель “М”, вводимый для искуственных переменных для ограничений “>” или “=”
‘Второй столбец, это коэфициенты переменных в целевой функции
‘(номера этих переменных указаны в третьем столбце массива MiCiXiAi)
‘Четвертый столбец массива MiCiXiAi(”Alfa”), это последний столбец симплексной таблицы равный X0/Хi
‘Two first columns of this array change the first column of the simplex table.
‘First column, this multiplier “M”, introduced for illusory variables for restrictions “>” or “=”
‘Second column, this values from target function
‘Second column is values variables in target function
‘(number these variables is specified in one third column array MiCiXiAi)
‘Fourth column of the array MiCiXiAi(”Alfa”), this last column of the simplex table equal X0/Hi
Dim Tsimp() As Double ‘ the simplex table
Dim CleaDoub() As Double
Dim CleaTMY() As Tmy
Dim Icol As Integer ’ Ключевой столбец.The Key column.
Dim Irow As Integer ’ Ключевая строка. The Key line.
Dim AllPlans As String ’Все планы в текущей задаче. All plans in the current task.
Dim DirectCycle As Boolean ‘True-Прямой цикл; True-Direct cycle;
Private Sub ProcString(Strin As String, Ans() As Tmy, CalcMaxX As Boolean)
‘Выделение из “Strin” числовых данных. Одновременно вычисляем махимальный индех переменно Х
‘Separation from “Strin” numeric data. Simultaneously we calculate the Largest number variable X.
Dim Awork() As Tmy
Dim VaLi As Double
Dim i As Integer ’ index in awork
Strin = Replace(Strin, ” “, “”) ‘ Убрали лишьние пробелы в целевой функции
Strin = Trim(Strin)
Strin = Replace(Strin, “X”, “x”) ‘Заменим все х на маленькое английское
Strin = Replace(Strin, “Х”, “x”) ‘Русское большое на маленькое английское x
Strin = Replace(Strin, “х”, “x”) ‘Русское маленькое на маленькое английское x
Strin = Replace(Strin, “>=”, “>”) ‘
Strin = Replace(Strin, “<=”, “<”) ‘
BgRight = 0
i = 0
Icurrent = 1
Do While BgRight = 0
i = i + 1
ReDim Preserve Awork(i)
VaLi = ExtractDbl(Strin, Icurrent)
Awork(i).KoefX = VaLi
VaLi = ExtractDbl(Strin, Icurrent)
Awork(i).IndX = CInt(VaLi)
If CalcMaxX Then If MaxX < CInt(VaLi) Then MaxX = CInt(VaLi)
Loop
Ans = Awork
End Sub
Private Sub CommandButton1_Click()
Dim i As Integer
Dim j As Integer
Dim K As Integer
Dim Acell As String
Dim St1 As String * 1
Dim Vdbl As Double
NumIter = 0
MaxX = 0
AllPlans = “”
DirectCycle = True
CommandButton1.ForeColor = &H40C0& ’Оранжевый
CommandButton1.Caption = “Привести к каноническому виду”
CommandButton1.Font = Bold
CommandButton1.Font.Size = 12
CommandButton1.Top = 1.5
CommandButton1.Left = 0.75
CommandButton1.Height = 24
CommandButton1.Width = 204
CommandButton2.ForeColor = &H8000& ’Зеленый
CommandButton2.Font = Bold
CommandButton2.Font.Size = 12
CommandButton2.Top = 1.5
CommandButton2.Left = 204
CommandButton2.Height = 24
CommandButton2.Width = 186
MiCiXiAi = CleaDoub
Rez = CleaTMY
Tsimp = CleaDoub
CommandButton2.Visible = False
Sheets(2).Name = “Пусто”
Sheets(2).Tab.ColorIndex = 6
‘Скроем все листы кроме первого. Первый лист переименуем в исходные данные.
‘We shall Hide all sheets except the first. The First sheet shall name “Initial data”.
‘For i = 3 To Sheets.Count
‘ Sheets(i).Visible = False
‘ Sheets(i).Visible = True
‘Next i
Sheets(1).Name = “Initial data”
‘определение количество строк с ограничениями
‘вычисление максимального индеха переменной Х (записіваем в MaxX).
‘Determination amount lines with restrictions
‘calculation the largest number variable X (record in MaxX).
Ftarget = Range(”A3″).Value
ProcString Ftarget, Rez, True
i = i
Isx = Trim(Range(”A9″).Value)
Do While Isx <> “”
ProcString Isx, Rez, True ’if True, then calculate MaxX
i = i + 1
Acell = “A” & CStr(i + 
Isx = Trim(Range(Acell).Value)
Loop
AmRest = i - 1
‘Получение значений целевой функции в массиве Rez
‘Reception of importances of the target function in array Rez
Ftarget = Range(”A3″).Value
ProcString Ftarget, Rez, False
i = InStr(Ftarget, “=”)
If i = 0 Then
MsgBox (”В целевой функции нет знака = “)
End
End If
If Mid(Ftarget, i + 1, 3) = “min” Then
MaxLi = False
ElseIf Mid(Ftarget, i + 1, 3) = “max” Then
MaxLi = True
Else
MsgBox (”В целевой функции нет ни ‘max’ ни ‘min’ “)
End
End If
‘ Запись значений целевой функции в симплекс таблицу
‘We write values of the target function in simplex table
ReDim Preserve Tsimp(AmRest + 3, MaxX)
ReDim Preserve MiCiXiAi(AmRest, 4)
For i = 1 To UBound(Rez)
j = Rez(i).IndX
Tsimp(0, j) = Rez(i).KoefX
Next
‘Получение значений условий в массиве Rez и запись их значения в симплекс таблицу
‘Reception of importances of the conditions in array Rez and record of their values in simplex table
For K = 1 To AmRest
Acell = “A” & CStr(K + 
Isx = Range(Acell).Value
ProcString Isx, Rez, False
For i = 1 To UBound(Rez)
j = Rez(i).IndX
Tsimp(K, j) = Rez(i).KoefX
Next i
Tsimp(K, 0) = Mid(Isx, BgRight) ’Правая часть ограничения. Right part of restriction.
St1 = Mid(Isx, BgRight - 1, 1)
‘ Если свободный член отрицателен, то следует изменить все значения на линии “K” в противоположном значении.
‘ If free member negative, that follows to change all importances on lines “K” in opposite importance
If Tsimp(K, 0) < 0 Then
For i = 0 To AmRest
Tsimp(K, i) = -Tsimp(K, i)
Next i
If St1 = “>” Then
St1 = “<”
ElseIf St1 = “<” Then
St1 = “>”
End If
End If
If St1 = “>” Then ‘ Если больше добавим 2 искуственных неизвестных
MaxX = MaxX + 2
ReDim Preserve Tsimp(AmRest + 3, MaxX)
Tsimp(K, MaxX - 1) = -1
Else ’Ограничение на равно или меньше
MaxX = MaxX + 1
ReDim Preserve Tsimp(AmRest + 3, MaxX)
End If
Tsimp(K, MaxX) = 1
If MaxLi And (St1 = “>” Or St1 = “=”) Then ’ Если махимум, в целевую функцию добавляем -Mxi, иначе +Mxi
Tsimp(AmRest + 3, MaxX) = -1 ‘ для > или =
ElseIf (Not MaxLi) And (St1 = “>” Or St1 = “=”) Then
Tsimp(AmRest + 3, MaxX) = 1
End If
MiCiXiAi(K, 1) = Tsimp(AmRest + 3, MaxX)
MiCiXiAi(K, 3) = MaxX
Next K
‘ Вычисление оценки
For j = 0 To MaxX
Vdbl = 0
For i = 1 To AmRest
Vdbl = Vdbl + MiCiXiAi(i, 1) * Tsimp(i, j)
Next i
Tsimp(AmRest + 1, j) = Vdbl - Tsimp(AmRest + 3, j)
Tsimp(AmRest + 2, j) = -Tsimp(0, j)
Next j
FRowCol
If Cycle() Then
MsgBox (”Неизвестная ошибка”)
End If
If Icol > 0 And Irow > 0 Then
LookResult “Каноническая таблица”, 31
ElseIf Icol > 0 And Irow <= 0 Then
LookResult “Функция не ограничена”, 28
Else
LookResult “Итерация невозможна”, 3
End If
End Sub
Private Sub LookResult(Sname As String, Fcolor As Integer)
‘Sheets(2).Tab.ColorIndex = 4
‘ Fcolor= 4-зеленый, 3-Красный, 37-Серосиний, 6-Желтый
‘ На втором листе начиная с ячейки A11 построим симплекс таблицу
‘ Вначале сделаем рамку
‘CreFrame(Vtop As Integer, Vleft As Integer, Vbottom As Integer, Vright As Integer)
Dim i As Integer, j As Integer
Dim Stk As String
Dim Sround As String
Sheets(2).Name = Sname
Sheets(2).Tab.ColorIndex = Fcolor
Sheets(2).Range(”a:iv”).Clear
CreFrame 11, 4, 11, MaxX + 3
CreFrame 12, 1, 12, MaxX + 4
CreFrame 12, 1, 12, 2
CreFrame 12, 4, 12, MaxX + 3
CreFrame 13, 1, 12 + AmRest, MaxX + 4
CreFrame 13, 4, 12 + AmRest, MaxX + 3
CreFrame 13, 3, 12 + AmRest, 3
CreFrame 13 + AmRest, 3, 13 + AmRest, MaxX + 4
CreFrame 13 + AmRest, 4, 13 + AmRest, MaxX + 3
CreFrame 14 + AmRest, 3, 14 + AmRest, MaxX + 4
CreFrame 14 + AmRest, 4, 14 + AmRest, MaxX + 3
‘Заполнение шапки симплексной таблицы
‘Filling the hat of the simplex table
For i = 0 To MaxX
Sheets(2).Cells(12, i + 3).Value = “X” + CStr(i)
Next i
If MaxLi Then Sheets(2).Cells(11, 3).Value = “F(Max)” Else Sheets(2).Cells(11, 3).Value = “F(Min)”
Sheets(2).Cells(12, 1).Value = “Сi”
Sheets(2).Cells(12, 2).Value = “P” + CStr(NumIter - 1)
Sheets(2).Cells(12, MaxX + 4).Value = “Alfa”
Sheets(2).Cells(13 + AmRest, 2).Value = “M–>”
‘Заполнение симплексной таблицы коэффициентами целевой функции
‘Filling the simplex table factor to target function
For j = 1 To MaxX
If Tsimp(AmRest + 3, j) = 0 Then
Sheets(2).Cells(11, j + 3).Value = Tsimp(0, j)
Else
If Tsimp(AmRest + 3, j) > 0 Then Sheets(2).Cells(11, j + 3).Value = ” M” Else Sheets(2).Cells(11, j + 3).Value = ” -M”
End If
Next j
‘Формирование первой, второй и последней колонок симплексной таблицы
‘Shaping first, second and last columnы of the simplex table
For i = 1 To AmRest
If MiCiXiAi(i, 1) = 0 Then
Sheets(2).Cells(12 + i, 1).Value = MiCiXiAi(i, 2)
ElseIf MiCiXiAi(i, 1) > 0 Then
Sheets(2).Cells(12 + i, 1).Value = ” M”
Else
Sheets(2).Cells(12 + i, 1).Value = ” -M”
End If
Sheets(2).Cells(12 + i, 2).Value = MiCiXiAi(i, 3)
Sheets(2).Cells(12 + i, MaxX + 4).Value = MiCiXiAi(i, 4)
Next i
‘Заполнение симплексной таблицы коэфициентами ограничений
‘Filling the simplex table koefficient restrictions
For i = 1 To AmRest + 2
For j = 0 To MaxX
Sheets(2).Cells(12 + i, j + 3).Value = Tsimp(i, j)
Next j
Next i
If Icol > 0 Then
‘ColourFrame(Vtop, Vleft, Vbottom, Vright, Vcolour=34)
ColourFrame 11, Icol + 3, AmRest + 14, Icol + 3, 34
End If
If Irow > 0 Then
ColourFrame Irow + 12, 2, Irow + 12, MaxX + 4, 34
End If
‘Информация об итерации или канонической таблице
‘Information on iterations or canonical table
If Fcolor = 31 Or Fcolor = 3 Then
Stk = “Начальная симплекс таблица задачи на ”
Stk = Stk & IIf(MaxLi, “максимум”, “минимум”) & “, приведенной к каноническому виду.”
With Sheets(2).Range(”A1″)
.Font.FontStyle = “Bold”
.Value = Stk
End With
Stk = IIf(Fcolor = 31, “Возможно улучшение плана.”, “Итерация невозможна(Видимо протероречивые условия).”)
Sheets(2).Range(”A2″).Value = Stk
Stk = “Разрешающий столбец определяется по двум последним строкам таблицы.”
Sheets(2).Range(”A3″).Value = Stk
Stk = “В пересечении колонок Х0-Х” & CStr(MaxX)
Stk = Stk & IIf(MaxLi, “(выбирается максимальное по модулю отрицательное число).”, “(выбирается максимальное положительное число).”)
Sheets(2).Range(”A4″).Value = Stk
Stk = “Сначала просматривается строка помеченная знаком “”M–>”" ”
Sheets(2).Range(”A5″).Value = Stk
Stk = ” и если в ней нет ” & IIf(MaxLi, “отрицательных”, “положительных”) & “чисел, просматривается последняя строка.”
Sheets(2).Range(”A6″).Value = Stk
Stk = “Если разрешающий столбец не нашли, то в таблице представлен оптимальный план.”
Sheets(2).Range(”A7″).Value = Stk
Stk = “Разрешающая строка определяется по минимальному не отрицательному отношению ”
Sheets(2).Range(”A8″).Value = Stk
Stk = “коэффициентов столбца Х0 и разрешающего столбца(что представлено в столбце Alfa).”
Sheets(2).Range(”A9″).Value = Stk
ElseIf Fcolor = 50 Then
Sheets(2).Range(”A1:A10″).ClearContents
Stk = “После итерации №” & CStr(NumIter - 1) & “(возможно улучшение плана) ”
With Sheets(2).Range(”A6″)
.Font.FontStyle = “Bold”
.Value = Stk
End With
i = IIf(Tsimp(AmRest + 1, Icol) = 0, 1, 2)
Stk = “Так как в ” & IIf(i = 1, “последней”, “предпоследней”) & “строке(начиная с колонки Х1)”
Sheets(2).Range(”A7″) = Stk
Stk = IIf(MaxLi, “(имеется максимальное по модулю отрицательное число).”, “(имеется максимальное положительное число).”)
Sheets(2).Range(”A8″) = Stk
Stk = “А в столбце “”Alfa”" имеется не отрицательное число(выбрано минимальное)”
Sheets(2).Range(”A9″) = Stk
ElseIf Fcolor = 37 Then
Stk = “После итерации №” & CStr(NumIter - 1) & ” получили оптимальный план. ”
j = IIf(Trim(CStr(Sheets(1).Range(”A5″).Value)) <> “”, CInt(Sheets(1).Range(”A5″).Value), -1) ‘j=-1 Without truncation
With Sheets(2).Range(”A5″)
.Font.FontStyle = “Bold”
.Value = Stk
End With
Sround = IIf(j = -1, CStr(Tsimp(AmRest + 2, 0)), CStr(Round(Tsimp(AmRest + 2, 0), j)))
Stk = “Для функции ” & Ftarget & ” результат равный ” & Sround
Sheets(2).Range(”A6″).Value = Stk
Stk = “Достигается при ”
For i = 1 To AmRest
If MiCiXiAi(i, 2) <> 0 Then
Sround = IIf(j = -1, CStr(Tsimp(i, 0)), CStr(Round(Tsimp(i, 0), j)))
Stk = Stk & “X” & CStr(MiCiXiAi(i, 3)) & “=” & Sround & “;”
End If
Next i
Sheets(2).Range(”A7″).Value = Stk
Stk = “Номера переменных Х и их значения находятся, соответственно, во второй и третьей колонках симплекс таблицы”
Sheets(2).Range(”A8″).Value = Stk
Stk = “Оптимальный план находится в первой ячейке последней строки симплекс таблицы”
Sheets(2).Range(”A9″).Value = Stk
End If
‘Округление Truncation
‘Количество знаков в дробной части в символьном виде
‘Amount sign in fractional part in symbol type
If Trim(CStr(Sheets(1).Range(”A5″).Value)) <> “” Then
j = CInt(Sheets(1).Range(”A5″).Value)
Sround = “0.”
For i = 1 To j
Sround = Sround & “0″
Next i
Stk = “C13:” & R1C1_to_A1(AmRest + 12, MaxX + 3)
Sheets(2).Range(Stk).NumberFormat = Sround
Stk = R1C1_to_A1(AmRest + 14, 3)
Sheets(2).Range(Stk).NumberFormat = Sround
End If
‘Viewing Canonical type
End Sub
Function ExtractDbl(Stk As String, ByVal iBg As Integer) As Double
‘поиск номера неизвестного xi(то есть вычисление i)
‘ номер i начинается от символа с номером iBg(включительно) и продолжается до одного из символов: +, -, =, >, <
‘Searching for of the number unknown xi(that is to say calculation i).
‘Number i begins from symbol with number iBg(inclusive) and lasts before one of the symbol: +, -, =, >, <
Dim SimIbg As String * 1
Dim i As Integer
Dim St1 As String * 1
For i = iBg To Len(Stk)
St1 = Mid(Stk, i, 1)
If i = iBg Then SimIbg = St1
If St1 = “x” Then
Icurrent = i + 1
Exit For
ElseIf (St1 = “+” Or St1 = “-”) And i <> iBg Then
Icurrent = i
Exit For
ElseIf St1 = “=” Or St1 = “>” Or St1 = “<” Then
Icurrent = i + 1
BgRight = i + 1
Exit For
End If
Next i
If i > Len(Stk) Then
MsgBox (”osibka in “”" & Stk & “”"”)
End
End If
If iBg = i Then
ExtractDbl = 1
ElseIf (i - iBg) = 1 And (SimIbg = “+” Or SimIbg = “-”) Then
If SimIbg = “+” Then ExtractDbl = 1 Else ExtractDbl = -1
Else
ExtractDbl = CDbl(Mid(Stk, iBg, i - iBg))
End If
End Function
‘Процедура CreFrame обрамляет область листа заданную кординатами
‘верхнего левого угла и координатами нижнего правого угла
‘ Procedure CreFrame does frame of the area of the sheet
‘given by coordinates of the upper left corner and coordinates of the right lower corner
Sub CreFrame(Vtop As Integer, Vleft As Integer, Vbottom As Integer, Vright As Integer)
Dim Stk As String
Stk = R1C1_to_A1(Vtop, Vleft) & “:” & R1C1_to_A1(Vbottom, Vright)
With Sheets(2).Range(Stk)
.Borders(xlEdgeLeft).Weight = xlThick
.Borders(xlEdgeRight).Weight = xlThick
.Borders(xlEdgeTop).Weight = xlThick
.Borders(xlEdgeBottom).Weight = xlThick
.Borders(xlInsideVertical).Weight = xlThin
.Borders(xlInsideHorizontal).Weight = xlThin
End With
End Sub
‘Процедура ColourFrame заполняет цветом область листа заданного координатами
‘верхнего левого угла и координатами правого нижнего угла
‘ The Procedure ColourFrame fills the colour an area sheet given by coordinates
‘ of the upper left corner and coordinates of the right lower corner.
Sub ColourFrame(Vtop As Integer, Vleft As Integer, Vbottom As Integer, Vright As Integer, Vcolour As Integer)
Dim Stk As String
Stk = R1C1_to_A1(Vtop, Vleft) & “:” & R1C1_to_A1(Vbottom, Vright)
Sheets(2).Range(Stk).Interior.ColorIndex = Vcolour ’Vcolour есть номер цвета в цветовой схеме.
‘ .ColorIndex = 34 ‘Vcolour there is number of the colour in color scheme.
End Sub
Function R1C1_to_A1(Vrow As Integer, Vcol As Integer) As String
V26 = “ABCDEFGHIJKLMNOPQRSTUVWXVZ”
Dim Stk As String
If Vcol > 26 Then
Stk = Mid(V26, Int(Vcol / 26), 1) + Mid(V26, (Vcol Mod 26), 1) + CStr(Vrow)
Else
Stk = Mid(V26, Vcol, 1) + CStr(Vrow)
End If
R1C1_to_A1 = Stk
End Function
Private Sub CalcColB()
‘Вычисление ключевого столбца по найбольшей оценке(когда min)
‘Calculation key column on the largest estimation(when min)
Dim i As Integer
Dim WrcM As Double, IrcM As Integer
Dim WrcC As Double, IrcC As Integer
WrcM = 0
WrcC = 0
For i = 1 To MaxX
If Tsimp(AmRest + 1, i) > WrcM Then
WrcM = Tsimp(AmRest + 1, i)
IrcM = i
ElseIf Tsimp(AmRest + 2, i) > WrcC And Tsimp(AmRest + 1, i) = 0 Then
WrcC = Tsimp(AmRest + 2, i)
IrcC = i
End If
Next i
If WrcM > 0 Then
Icol = IrcM
ElseIf WrcC > 0 Then
Icol = IrcC
Else
Icol = 0
End If
End Sub
Private Sub CalcColL()
‘Вычисление ключевого столбца по отрицательной(максимальной по модулю) оценке(когда max)
‘Calculation key column on negative(maximum modulo) to estimation(when max)
Dim i As Integer
Dim WrcM As Double, IrcM As Integer
Dim WrcC As Double, IrcC As Integer
WrcM = 0
WrcC = 0
For i = 1 To MaxX
If Tsimp(AmRest + 1, i) < 0 And Abs(Tsimp(AmRest + 1, i)) > WrcM Then
WrcM = Abs(Tsimp(AmRest + 1, i))
IrcM = i
ElseIf (Tsimp(AmRest + 2, i) < 0) And (Abs(Tsimp(AmRest + 2, i)) > WrcC) And (Tsimp(AmRest + 1, i) = 0) Then
WrcC = Abs(Tsimp(AmRest + 2, i))
IrcC = i
End If
Next i
If WrcM > 0 Then
Icol = IrcM
ElseIf WrcC > 0 Then
Icol = IrcC
Else
Icol = 0
End If
End Sub
Private Sub CalcRow()
‘Вычисление ключевой строки по положительному минимум отношения X0/Xi
‘Calculation of the key line on positive minimum relations X0/Xi
Dim Cslave As Double, Islave As Integer
Dim Wrk As Double
If Icol = 0 Then
For i = 1 To AmRest
MiCiXiAi(i, 4) = -1
‘MiCiXiAi(i, 4) = Nothing
Next i
Irow = 0
Else
Cslave = -1
Islave = 0
For i = 1 To AmRest
If Tsimp(i, Icol) <> 0 Then
If Tsimp(i, 0) = 0 Then
Wrk = IIf(Sgn(Tsimp(i, Icol)) = 1, 0, -1)
Else
Wrk = Tsimp(i, 0) / Tsimp(i, Icol)
End If
MiCiXiAi(i, 4) = Wrk
If Wrk >= 0 And Islave = 0 Then
Cslave = Wrk
Islave = i
ElseIf Wrk >= 0 Then
If DirectCycle Then
If Wrk < Cslave Then ’оставлять из равных первый
Cslave = Wrk
Islave = i
End If
Else
If Wrk <= Cslave Then ‘оставлять из равных последний
Cslave = Wrk
Islave = i
End If
End If
End If
Else
MiCiXiAi(i, 4) = -1
End If
Next i
Irow = Islave
End If
End Sub
Private Sub CommandButton2_Click()
‘Совершить итерацию
Dim Welm As Double
MiCiXiAi(Irow, 1) = Tsimp(AmRest + 3, Icol)
MiCiXiAi(Irow, 2) = Tsimp(0, Icol)
MiCiXiAi(Irow, 3) = Icol
Welm = Tsimp(Irow, Icol)
For i = 1 To AmRest + 2
If i <> Irow Then
For j = 0 To MaxX
If j <> Icol Then
Tsimp(i, j) = Tsimp(i, j) - (Tsimp(i, Icol) / Welm) * Tsimp(Irow, j)
End If
Next j
End If
Next i
For j = 0 To MaxX
Tsimp(Irow, j) = Tsimp(Irow, j) / Welm
Next j
For i = 1 To AmRest + 2
Tsimp(i, Icol) = 0
Next i
Tsimp(Irow, Icol) = 1
FRowCol
If Cycle() Then
LookResult “Итерации зациклились на итерации №” & CStr(NumIter - 1), 11
ElseIf Icol > 0 And Irow > 0 Then
LookResult “Смотри итерацию №” & CStr(NumIter - 1), 50
ElseIf Icol > 0 And Irow <= 0 Then
LookResult “Функция не ограничена”, 28
Else
LookResult “Оптимальный план”, 37
End If
End Sub
Private Sub FRowCol()
‘Поиск разрешающих строки и столбца
If MaxLi Then
CalcColL ’max
Else
CalcColB ’ min
End If
CalcRow ’X0/Xi
If Icol > 0 And Irow > 0 Then
CommandButton2.Visible = True
NumIter = NumIter + 1
CommandButton2.Caption = “Произвести итерацию №” & CStr(NumIter)
Else
NumIter = NumIter + 1
CommandButton2.Visible = False
End If
End Sub
Private Function Cycle() As Boolean ‘Если “Верно” зациклились. If “True” were looped.
Dim CurrentPlan As String
Dim i As Integer
Cycle = False
CurrentPlan = “”
For i = 1 To AmRest
CurrentPlan = CurrentPlan & CStr(MiCiXiAi(i, 3))
Next i
If InStr(AllPlans, CurrentPlan) > 0 Then
If DirectCycle = True Then
DirectCycle = False
Else
Cycle = True
End If
AllPlans = “”
Else
AllPlans = AllPlans & ” ” & CurrentPlan
End If
End Function
Заключение
В данной работе рассматриваются два способа решения исходной задачи линейного программирования.
Первый заключается в том, что сначала решается вспомогательная задача (L-задача), позволяющая построить начальный опорный план, затем на основе этого найденного плана решается исходная задача (определяется ее оптимальный план). Второй способ является объединением двух этапов и состоит в решении расширенной задачи (M-задачи), также приводящей к нахождению оптимального плана исходной задачи.
Вычислительную основу этих двух способов решения составляют соответственно первый и второй алгоритмы симплекс-метода. Один из параметров, по которому может быть оценен любой итерационный алгоритм – количество шагов, приводящих к решению задачи или установлению ее неразрешимости. Для данной задачи наиболее эффективным методом оказался первый метод(L-задача + исходная задача), т.к. он привел к решению за 4 шага, а второй метод (M-задача) за 5 шагов. Разница в числе шагов, вероятно, обусловлена неоднозначность выбора разрешающего элемента в исходной таблице L-задачи.
Сравнение количества вычислений на каждой итерации приводит к следующим оценочным результатам рассматриваемых алгоритмов. Преимущественная часть вычислений на каждом шаге алгоритмов определяется размерностью главной части таблицы (в первом алгоритме) или основной таблицы (во втором алгоритме). В первом случае она имеет размерность (m+1)x(n+1), во втором - (m+1)x(m+1). Даже учитывая, что второй алгоритм требует построения вспомогательной таблицы, он оказывается более компактным.
Еще одно несомненное достоинство второго алгоритма заключается в возможности определения оптимального плана двойственной задачи из (m+1)-й строки основной таблицы, соответствующей последней итерации, без всяких дополнительных вычислений.
Список использованных источников
Вентцель Е.С.
Исследование операций: задачи, принципы, методология. – М.: Высшая школа, 2001.
Аронович А.Б., Афанасьев М.Ю., Суворов Б.П.
Сборник задач по исследованию операций. – М.: Издательство Московского университета, 1997.
Исследование операций в экономике /Под ред. Кремер. – М.:
ЮНИТИ, 1997.
Морозов В.В., Сухарев А.Г., Федоров В.В.
Исследование операций в задачах и упражнениях. – М.: Высшая школа, 1986.
Шикин Е.В., Чхартишвили А.Г.
Математические методы и модели управления. – М.: Дело, 2000.
Акулич И.Л.
Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
Филлипс Д., Гарсиа-Диас А.
Методы анализа сетей. – М.: Мир, 1984.
Липски В.
Комбинаторика для программистов. – М.: Мир, 1988.
30
|