Министерство образования Российской Федерации
Ставропольский Государственный университет
Кафедра математического анализа
Курсовая работа на тему :
«Дзета-функция Римана»
Выполнил: студент 2го
курса ФМФ группы «Б» Симонян Сергей Олегович
Ставрополь, 2004 г.
Введение.
Функция – одно из основных понятий во всех естественнонаучных дисциплинах. Не случайно ещё в средней школе дети получают интуитивное представление об этом понятии. Со школьной скамьи наш багаж знаний пополняется сведениями о таких функциях как линейная, квадратичная, степенная, показательная, тригонометрические и других. В курсе высшей математики круг известных функций значительно расширяется. Сюда добавляются интегральные и гиперболические функции, эйлеровы интегралы (гамма- и бета-функции), тета-функции, функции Якоби и многие другие.
Что же такое функция? Строгого определения для неё не существует. Это понятие является в математике первичным, аксиоматизируется. Однако, под функцией понимают закон, правило, по которому каждому элементу какого-то множества X
ставится в соответствие один или несколько элементов множества Y
. Элементы множества X
называются аргументами, а множества Y
– значениями функции. Если каждому аргументу соответствует одно значение, функция называется однозначной, если более одного – то многозначной. Синонимом функции является термин «отображение». В простейшем случае множество X
может быть подмножеством поля действительных R
или комплексных C
чисел. Тогда функция называется числовой. Нам будут встречаться только такие отображения.
Функции могут быть заданы многими различными способами: словесным, графическим, с помощью формулы. Функция, которую мы будем рассматривать в этой работе, задаётся через бесконечный ряд. Но, несмотря на такое нестандартное определение, по своему представлению в виде ряда она может быть хорошо изучена методами теории рядов и плодотворно применена к различным теоретическим и прикладным вопросам математики и смежных с ней наук.
Конечно же, речь идёт о знаменитой дзета-функции Римана, имеющей широчайшие применения в теории чисел. Впервые ввёл её в науку великий швейцарский математик и механик Леонард Эйлер и получил многие её свойства. Далее активно занимался изучением дзета-функции немецкий математик Бернгард Риман. В честь него она получила своё название, так как он опубликовал несколько исключительно выдающихся работ, посвящённых этой функции. В них он распространил дзета-функцию на область комплексных чисел, нашёл её аналитическое продолжение, исследовал количество простых чисел, меньших заданного числа, дал точную формулу для нахождения этого числа с участием функции 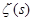 и высказал свою гипотезу о нулях дзета-функции, над доказательством или опровержением которой безрезультатно бьются лучшие умы человечества уже почти 150 лет. и высказал свою гипотезу о нулях дзета-функции, над доказательством или опровержением которой безрезультатно бьются лучшие умы человечества уже почти 150 лет.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Научная общественность считала и считает решение этой проблемы одной из приоритетных задач. Так Давид Гильберт, выступавший на Международной Парижской математической конференции 1900 году с подведением итогов развития науки и рассмотрением планов на будущее, включил гипотезу Римана в список 23 проблем, подлежащих решению в новом столетии и способных продвинуть науку далеко вперёд. А на рубеже веков, в 2000 году американский The Clay Mathematics Institute назвал семь задач, за решение каждой из которых будет выплачен 1 миллион долларов. В их число также попала гипотеза Римана.
Таким образом, даже бы поверхностное знакомство с дзета-функцией будет и интересным, и полезным.
Глава 1.
Итак, приступим к изучению этой важной и интересной дзета-функции Римана. В данной главе мы получим некоторые свойства функции в вещественной области, исходя из её определения с помощью ряда.
Определение.
Дзета-функцией Римана ζ(
s
)
называют функцию, которая любому действительному числу s
ставит в соответствие сумму ряда
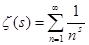 (1) (1)
если она существует.
Основной характеристикой любой функции является область определения. Найдём её для нашей функции.
Пусть сначала s
≤
0, тогда s
=−t
, где t
принадлежит множеству неотрицательных действительных чисел R
+
 {0}. В этом случае {0}. В этом случае 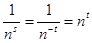 и ряд (1) обращается в ряд и ряд (1) обращается в ряд 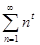 , который, очевидно, расходится как при t
>0, так и при t
=0. То есть значения s
≤
0 не входят в область определения функции. , который, очевидно, расходится как при t
>0, так и при t
=0. То есть значения s
≤
0 не входят в область определения функции.
Теперь пусть s
>0. Для исследования сходимости ряда (1) воспользуемся интегральным признаком Коши. При каждом s
рассмотрим функцию 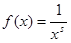 , где , где 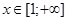 , которая является на промежутке непрерывной, положительной и монотонно убывающей. Возникает три различных возможности: , которая является на промежутке непрерывной, положительной и монотонно убывающей. Возникает три различных возможности:
1) 0<s
<1. Тогда 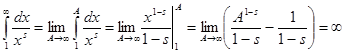 , поэтому ряд (1) расходится и промежуток (0;1) не входит в область определения дзета-функции; , поэтому ряд (1) расходится и промежуток (0;1) не входит в область определения дзета-функции;
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
2) s
=1. Получаем 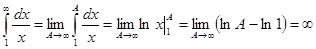 , то есть при s
=1 дзета-функция Римана также не определена; , то есть при s
=1 дзета-функция Римана также не определена;
3) s
>1. В этом случае 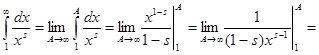
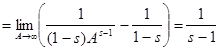 . Ряд (1) сходится. . Ряд (1) сходится.
Обобщив результаты, находим, что область определения дзета-функции есть промежуток 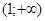 . На этом промежутке функция оказывается непрерывной и дифференцируемой бесконечное число раз. . На этом промежутке функция оказывается непрерывной и дифференцируемой бесконечное число раз.
Докажем непрерывность функции ζ(
s
)
на области определения. Возьмём произвольное число s
0
>1. Перепишем ряд (1) в виде 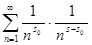 . Как было выше показано, ряд . Как было выше показано, ряд 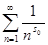 сходится, а функции сходится, а функции 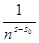 при s
>s
0
монотонно убывают и все вместе ограничены единицей. Значит, по признаку Абеля для s
>s
0
ряд (1) сходится равномерно. Используя теорему о непрерывности суммы функционального ряда, получаем, что в любой точке s
>s
0
дзета-функция непрерывна. Ввиду произвольности s
0
ζ
(
s
)
непрерывна на всей области определения. при s
>s
0
монотонно убывают и все вместе ограничены единицей. Значит, по признаку Абеля для s
>s
0
ряд (1) сходится равномерно. Используя теорему о непрерывности суммы функционального ряда, получаем, что в любой точке s
>s
0
дзета-функция непрерывна. Ввиду произвольности s
0
ζ
(
s
)
непрерывна на всей области определения.
Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана:
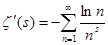 (2). (2).
Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке 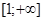 и воспользоваться теоремой о дифференцировании рядов. Используем тот же приём. Зафиксируем любое s
0
>1 и представим ряд (2) в виде и воспользоваться теоремой о дифференцировании рядов. Используем тот же приём. Зафиксируем любое s
0
>1 и представим ряд (2) в виде 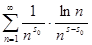 для s
>s
0
. Множители для s
>s
0
. Множители 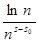 , начиная с n
=2, монотонно убывают, оставаясь ограниченными числом ln 2. Поэтому по признаку Абеля ряд (2) сходится равномерно при s
>
s
0
, а значит и при любом s
>1. Какое бы значение s
>1 ни взять его можно заключить между , начиная с n
=2, монотонно убывают, оставаясь ограниченными числом ln 2. Поэтому по признаку Абеля ряд (2) сходится равномерно при s
>
s
0
, а значит и при любом s
>1. Какое бы значение s
>1 ни взять его можно заключить между 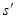 и и 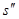 , где , где 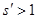 , а , а 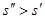 ; к промежутку ; к промежутку 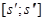 применима вышеуказанная теорема. применима вышеуказанная теорема.
Таким же путём можно убедиться в существовании для дзета-функции производных всех порядков и получить их выражения в виде рядов:
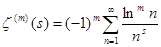 . .
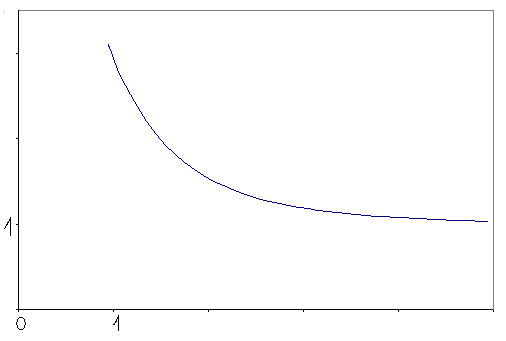
Попытаемся построить наглядное изображение функции в виде графика. Для этого изучим сначала её поведение на бесконечности и в окрестности точки s
=1.
В первом случае, ввиду равномерной сходимости ряда (1), по теореме о почленном переходе к пределу, имеем 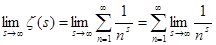 . При n
=1 предел равен единице, остальные пределы равны нулю. Поэтому . При n
=1 предел равен единице, остальные пределы равны нулю. Поэтому 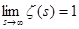 . .
Чтобы исследовать случай 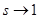 , докажем некоторые вспомогательные оценки. , докажем некоторые вспомогательные оценки.
Во-первых, известно, что если для ряда 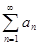 существует непрерывная, положительная, монотонно убывающая функция существует непрерывная, положительная, монотонно убывающая функция 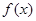 , определённая на множестве , определённая на множестве 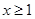 , такая, что , такая, что 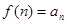 , и имеет первообразную , и имеет первообразную 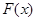 , то остаток ряда оценивается так: , то остаток ряда оценивается так: 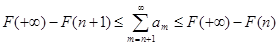 , где , где 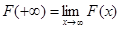 . Применяя вышесказанное к ряду (1), найдём, что необходимая функция . Применяя вышесказанное к ряду (1), найдём, что необходимая функция
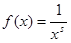 , а , а 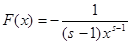 и и 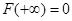 . Отсюда, подставляя в двойное неравенство, имеем . Отсюда, подставляя в двойное неравенство, имеем
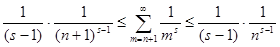 (3). В левом неравенстве положим n
=0, тогда (3). В левом неравенстве положим n
=0, тогда 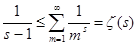 , то есть , то есть 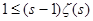 . В правом же возьмём n
=1 и получим . В правом же возьмём n
=1 и получим 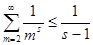 , далее , далее 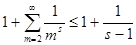 , , 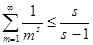 и, наконец, и, наконец, 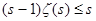 . Переходя в неравенствах . Переходя в неравенствах 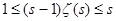 к пределу при к пределу при 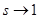 , находим , находим 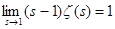 . .
Отсюда, в частности, следует, что 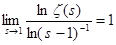 . Действительно, положим . Действительно, положим 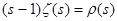 . Тогда . Тогда 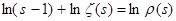 , то есть , то есть 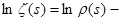 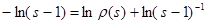 . Поэтому . Поэтому 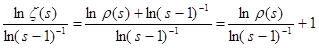 . Из того, что . Из того, что 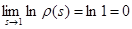 , а , а 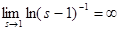 , вытекает доказываемое утверждение. , вытекает доказываемое утверждение.
Можно, однако, получить ещё более точный результат для оценки поведения дзета-функции в окрестности единицы, чем приведённые выше, принадлежащий Дирихле. Будем отталкиваться от очевидного при произвольном n
равенства 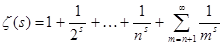 . Прибавим ко всем частям неравенств (3) сумму . Прибавим ко всем частям неравенств (3) сумму 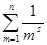 и вычтем и вычтем 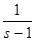 . Имеем . Имеем 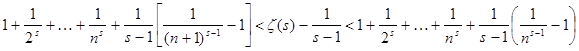 . Пусть здесь s
стремится к единице. По правилу Лопиталя легко вычислить . Пусть здесь s
стремится к единице. По правилу Лопиталя легко вычислить 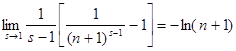 и и 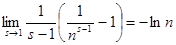 . Мы пока не знаем, существует ли предел выражения . Мы пока не знаем, существует ли предел выражения 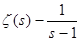 при при 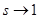 , поэтому, воспользовавшись наибольшим и наименьшим пределами, напишем неравенства так: , поэтому, воспользовавшись наибольшим и наименьшим пределами, напишем неравенства так: 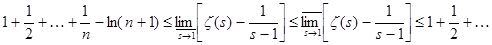
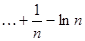 . Ввиду произвольности n
возьмём . Ввиду произвольности n
возьмём 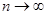 . Первое и последнее выражения стремятся к эйлеровой постоянной C (C . Первое и последнее выражения стремятся к эйлеровой постоянной C (C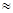 0,577). Значит 0,577). Значит 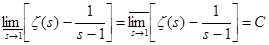 , а, следовательно, существует и обычный предел и , а, следовательно, существует и обычный предел и 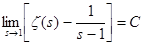 . .
Найденные выше пределы позволяют получить лишь приблизительное представление о виде графика дзета-функции. Сейчас мы выведем формулу, которая даст возможность нанести на координатную плоскость конкретные точки, а именно, определим значения 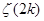 , где k
– натуральное число. , где k
– натуральное число.
Возьмём известное разложение 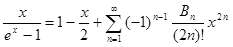 , где , где 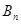 - знаменитые числа Бернулли (по сути, через него эти числа и определяются). Перенесём слагаемое - знаменитые числа Бернулли (по сути, через него эти числа и определяются). Перенесём слагаемое 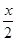 в левую часть равенства. Слева получаем в левую часть равенства. Слева получаем 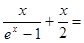 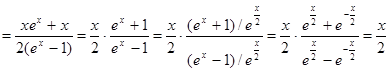 cth cth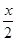 , а в правой части - , а в правой части -  , то есть , то есть 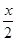 cth cth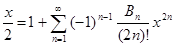 . Заменяем . Заменяем 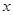 на на 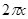 , получаем , получаем 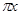 cth cth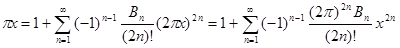 . .
С другой стороны, существует равенство cth , из которого , из которого 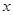 cth cth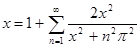 . Подстановкой . Подстановкой  вместо вместо 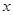 находим находим 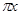 cth cth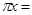 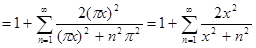 . Если . Если 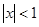 , то для любого , то для любого 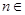 N N
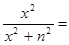 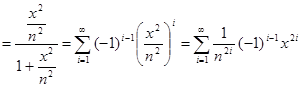 и по теореме о сложении бесконечного множества степенных рядов и по теореме о сложении бесконечного множества степенных рядов 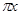 cth cth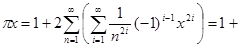 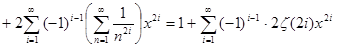 . .
Приравняем полученные разложения: 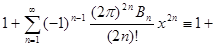
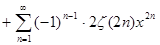 , следовательно , следовательно 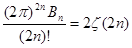 . Отсюда немедленно следует искомая формула . Отсюда немедленно следует искомая формула
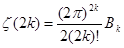 (4), где (4), где 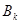 - k
-е число Бернулли. Она удобна тем, что эти числа хорошо изучены и для них составлены обширные таблицы. - k
-е число Бернулли. Она удобна тем, что эти числа хорошо изучены и для них составлены обширные таблицы.
Теперь, исходя из полученных результатов, можно построить эскиз графика дзета-функции Римана, достаточно хорошо отражающий её поведение на всей области определения.
Леонард Эйлер, впервые рассмотревший дзета-функцию, получил замечательное разложение её в бесконечное произведение, которое иногда тоже принимают за определение:
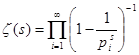 , где pi
– i
-е простое число (4). , где pi
– i
-е простое число (4).
Докажем тождественность ряда (1) и произведения (4). Вспомнив формулу суммы геометрической прогрессии, получаем равенство 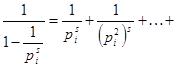
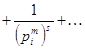 Если перемножить конечное число таких рядов, отвечающих всем простым числам, не превосходящим заданного натурального числа N
, то получившееся частичное произведение окажется равным Если перемножить конечное число таких рядов, отвечающих всем простым числам, не превосходящим заданного натурального числа N
, то получившееся частичное произведение окажется равным  , где символ * означает, что суммирование распространяется не на все натуральные числа, а лишь на те из них (не считая единицы), которые в своём разложении содержат только простые числа меньшие N
. Так как первые N
натуральных чисел этим свойством обладают, то , где символ * означает, что суммирование распространяется не на все натуральные числа, а лишь на те из них (не считая единицы), которые в своём разложении содержат только простые числа меньшие N
. Так как первые N
натуральных чисел этим свойством обладают, то
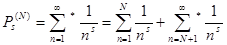 (5). (5).
Сумма 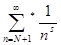 содержит не все числа, большие N
+1, поэтому, очевидно, содержит не все числа, большие N
+1, поэтому, очевидно, 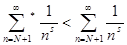 . Из (5) получаем . Из (5) получаем
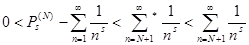 (6). (6).
Ввиду сходимости ряда (1), выражение справа, представляющее его остаток после N
-го члена, стремится к нулю при N
стремящимся к бесконечности, а 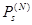 есть произведение (4). Значит из неравенства при есть произведение (4). Значит из неравенства при 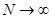 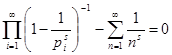 , что и требовалось доказать. , что и требовалось доказать.
Формула (4) важна потому, что она связывает натуральный ряд, представленный множеством значений аргумента дзета-функции, со множеством простых чисел. Ещё один шаг в этом направлении мы сделаем, оценив 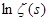 , а именно показав, что , а именно показав, что 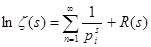 , где , где 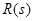 остаётся ограниченным при остаётся ограниченным при 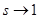 . .
Из (4) следует, что 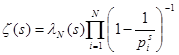 , где , где 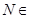 N
, а N
, а 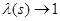 при при 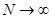 . Возьмём логарифм от обеих частей равенства, тогда . Возьмём логарифм от обеих частей равенства, тогда 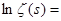 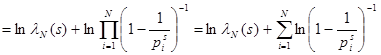 . Натуральные логарифмы под знаком суммы разлагаются в ряд: . Натуральные логарифмы под знаком суммы разлагаются в ряд: 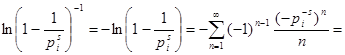 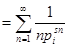 . Подставив полученные разложения в равенство и устремив N
к бесконечности, имеем . Подставив полученные разложения в равенство и устремив N
к бесконечности, имеем 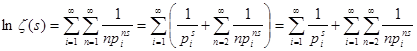 . Остаётся доказать ограниченность последнего слагаемого. Ясно, что . Остаётся доказать ограниченность последнего слагаемого. Ясно, что 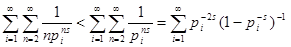 . Последнее равенство справедливо, так как . Последнее равенство справедливо, так как 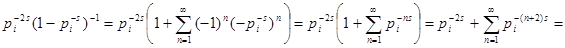 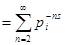 . Далее, очевидно, . Далее, очевидно, 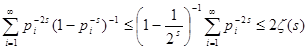 , что и завершает доказательство. , что и завершает доказательство.
На этом закончим изложение свойств дзета-функции Римана для действительного аргумента, так как наибольший теоретический и прикладной интерес представляет случай изложенный во второй главе.
Глава 2.
Все результаты первой главы, касающиеся дзета-функции Римана, были получены в предположении, что её аргумент s
– действительное число. Однако, самые выдающиеся исследования и многочисленные важные приложения стали возможны лишь после включения в область определения функции комплексных чисел. Впервые рассмотрел дзета-функцию как функцию мнимого аргумента немецкий математик Бернгард Риман, глубоко изучивший её свойства и широко применявший её в теории чисел. В честь него функция получила своё название.
Для комплексной дзета-функции остаётся в силе определение, данное в главе 1, с тем лишь изменением, что теперь там будет 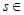 C
.
Возникает необходимость найти новую область определения. С этой целью докажем следующее утверждение: в полуплоскости C
.
Возникает необходимость найти новую область определения. С этой целью докажем следующее утверждение: в полуплоскости 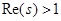 ( (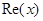 действительная часть числа x
) ряд действительная часть числа x
) ряд
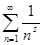 (1) сходится абсолютно. (1) сходится абсолютно.
Пусть 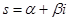 . Подсчитаем абсолютные величины членов ряда (1), . Подсчитаем абсолютные величины членов ряда (1), 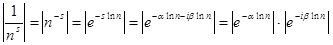 . Первый множитель содержит только вещественные числа и . Первый множитель содержит только вещественные числа и 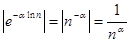 , так как , так как 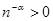 . Ко второму же множителю применим знаменитую формулу Эйлера, получим . Ко второму же множителю применим знаменитую формулу Эйлера, получим 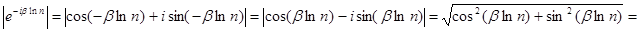 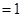 . Значит, . Значит, 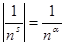 . Ввиду сходимости ряда . Ввиду сходимости ряда  при α>1, имеем абсолютную сходимость ряда (1). при α>1, имеем абсолютную сходимость ряда (1).
На своей области определения дзета-функция аналитична. Действительно, при всяком q
>0 и фиксированном α>1+q
, числовой ряд 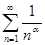 мажорирует ряд из абсолютных величин мажорирует ряд из абсолютных величин 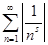 , где , где 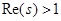 , откуда, по теореме Вейерштрасса, следует равномерная сходимость ряда в полуплоскости , откуда, по теореме Вейерштрасса, следует равномерная сходимость ряда в полуплоскости 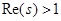 . Сумма же равномерно сходящегося ряда из аналитических функций сама является аналитической функцией. . Сумма же равномерно сходящегося ряда из аналитических функций сама является аналитической функцией.
Нетрудно показать, что все полученные для дзета-функции формулы без изменений переносятся на случай комплексного аргумента. Доказательства претерпевают незначительные преобразования, связанные с переходом к абсолютным величинам.
В связи с этим замечанием становится возможным использовать разложение дзета-функции в произведение 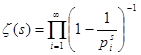 , где s
теперь любое комплексное число, такое, что , где s
теперь любое комплексное число, такое, что 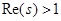 . Применим его к доказательству отсутствия у функции . Применим его к доказательству отсутствия у функции 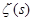 корней. корней.
Оценим величину  , используя свойство модуля , используя свойство модуля 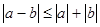 : : 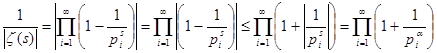 , где как обычно , где как обычно 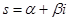 . Так как . Так как 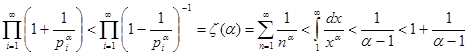 , то , то 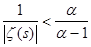 , а , а 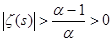 , следовательно, дзета-функция в нуль не обращается. , следовательно, дзета-функция в нуль не обращается.
Вопрос о нулях дзета-функции, а также другие прикладные вопросы получают новые широкие возможности для исследования, если распространить её на всю комплексную плоскость. Поэтому, сейчас мы одним из многих возможных способов найдём аналитическое продолжение дзета-функции и выведем её функциональное уравнение, характеризующее и однозначно определяющее 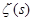 . .
Для этого нам понадобится формула
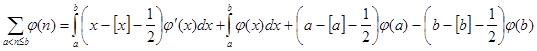 (2), которая выводится следующим образом. Используя свойства интегралов можно записать (2), которая выводится следующим образом. Используя свойства интегралов можно записать 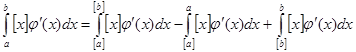 . Для любого d
при . Для любого d
при 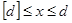 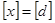 , значит , значит 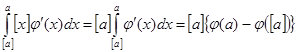 и и 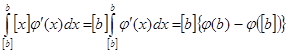 , а , а 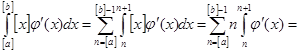 . . 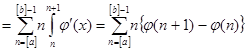 . Следовательно, . Следовательно, 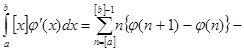 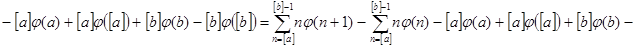 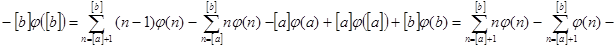  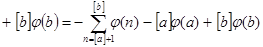 . Интеграл . Интеграл 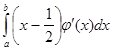 можно найти интегрированием по частям, принимая можно найти интегрированием по частям, принимая 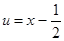 , , 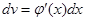 ; тогда ; тогда 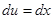 , а , а 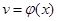 . В результате . В результате 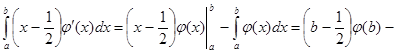 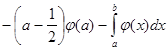 . Вычтем из этого интеграла предыдущий и получим . Вычтем из этого интеграла предыдущий и получим 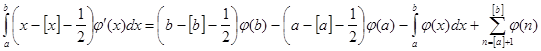 , отсюда легко следует равенство (2). , отсюда легко следует равенство (2).
Теперь положим в (2) 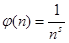 , , 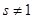 , a
и b
– целые положительные числа. Тогда , a
и b
– целые положительные числа. Тогда 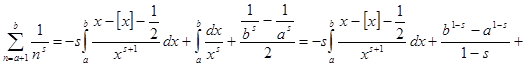 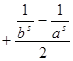 . Пусть сначала . Пусть сначала 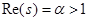 , примем a
=1, а b
устремим к бесконечности. Получим , примем a
=1, а b
устремим к бесконечности. Получим 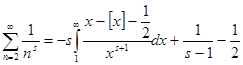 . Прибавим по единице в обе части равенств: . Прибавим по единице в обе части равенств:
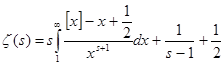 (3). (3).
Выражение  является ограниченным, так как является ограниченным, так как 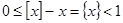 , а функция , а функция 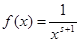 абсолютно интегрируема на промежутке абсолютно интегрируема на промежутке 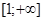 при при 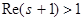 , то есть при , то есть при  , , 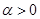 . Значит, интеграл . Значит, интеграл 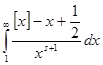 абсолютно сходится при абсолютно сходится при 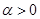 , причём равномерно в любой конечной области, лежащей в комплексной плоскости справа от прямой , причём равномерно в любой конечной области, лежащей в комплексной плоскости справа от прямой  . Тем самым он определяет аналитическую функцию переменной s
, регулярную при . Тем самым он определяет аналитическую функцию переменной s
, регулярную при 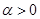 . Поэтому правая часть равенства (3) представляет собой аналитическое продолжение дзета-функции на полуплоскость . Поэтому правая часть равенства (3) представляет собой аналитическое продолжение дзета-функции на полуплоскость 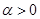 и имеет там лишь один простой полюс в точке и имеет там лишь один простой полюс в точке 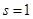 с вычетом, равным единице. с вычетом, равным единице.
Для 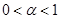 можно преобразовать выражение (3) дзета-функции. При можно преобразовать выражение (3) дзета-функции. При 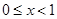 имеем имеем 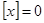 , значит, , значит, 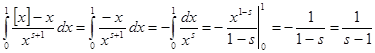 и и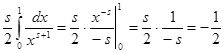 . Теперь при . Теперь при 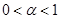 (3) может быть записано в виде (3) может быть записано в виде 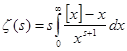 . .
Немного более сложными рассуждениями можно установить, что в действительности (3) даёт аналитическое продолжение дзета-функции на полуплоскость 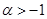 . Положим . Положим 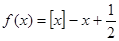 , а , а 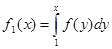 , то есть , то есть 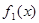 первообразная для первообразная для 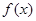 . . 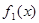 ограничена, так как ограничена, так как 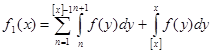 , а интеграл , а интеграл 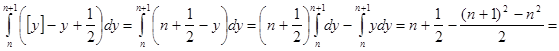 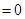 и и 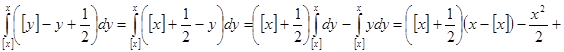 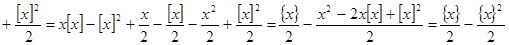 ограничен из-за того, что ограничен из-за того, что 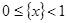 . Рассмотрим интеграл . Рассмотрим интеграл 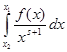 при x
1
>x
2
и при x
1
>x
2
и 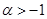 . Проинтегрируем его по частям, приняв . Проинтегрируем его по частям, приняв 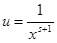 , , 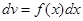 , тогда , тогда 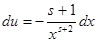 , а по указанному выше утверждению , а по указанному выше утверждению 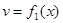 . Получаем . Получаем 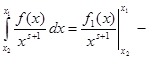 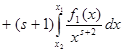 . Возьмём . Возьмём 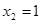 , а , а 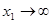 . Имеем . Имеем 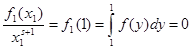 , , 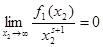 , потому что , потому что 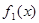 является ограниченной функцией. Значит, является ограниченной функцией. Значит,
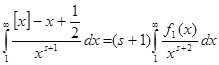 (4). (4).
Пользуясь абсолютной сходимостью интеграла 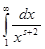 , если , если 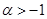 , и ограниченностью функции , и ограниченностью функции 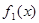 , делаем вывод, что в левой части равенства (4) интеграл тоже сходится при , делаем вывод, что в левой части равенства (4) интеграл тоже сходится при 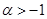 . Значит формулой (3) можно продолжить дзета-функцию и на полуплоскость правее прямой . Значит формулой (3) можно продолжить дзета-функцию и на полуплоскость правее прямой 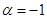 . .
Нетрудно установить, что для отрицательных 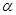 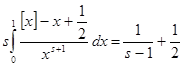 , поэтому из (3) имеем , поэтому из (3) имеем
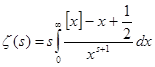 (5) при (5) при 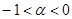 . .
Из теории рядов Фурье известно, что для нецелых значений x
справедливо разложение в ряд
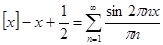 (6). (6).
Подставим его в равенство (5) и проинтегрируем ряд почленно:
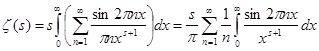 . Сделаем в полученном интеграле подстановку . Сделаем в полученном интеграле подстановку 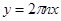 , отсюда следует , отсюда следует 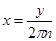 , а , а 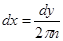 , и получим далее , и получим далее 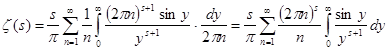 . Известно, что . Известно, что 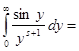 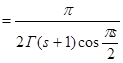 , значит , значит 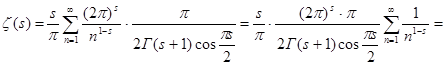 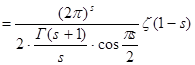 . Из известного соотношения для гамма-функции . Из известного соотношения для гамма-функции 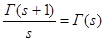 , по формуле дополнения , по формуле дополнения 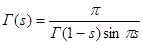 , следовательно , следовательно 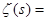 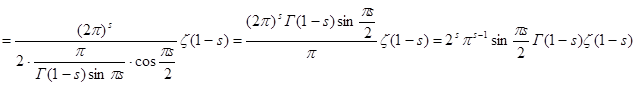
Итак, мы получили функциональное уравнение дзета-функции Римана
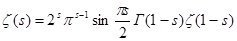 (7), (7),
которое само по себе может служить средством изучения этой функции, так как вполне характеризует её, в том смысле, что любая другая функция 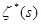 , удовлетворяющая равенству (7), а также ещё некоторым естественным условиям, тождественна с , удовлетворяющая равенству (7), а также ещё некоторым естественным условиям, тождественна с 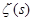 . .
Пока, правда, как следует из рассуждений, мы доказали формулу (7) для 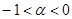 . Однако правая часть этого равенства является аналитической функцией s
и при . Однако правая часть этого равенства является аналитической функцией s
и при 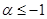 . Это показывает, что дзета-функция может быть аналитически продолжена на всю комплексную плоскость, причём не имеет на ней никаких особенностей, кроме упоминавшегося полюса при . Это показывает, что дзета-функция может быть аналитически продолжена на всю комплексную плоскость, причём не имеет на ней никаких особенностей, кроме упоминавшегося полюса при 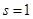 . .
Чтобы доказательство было строгим, мы должны ещё обосновать почленное интегрирование. Поскольку ряд (6) сходится почти всюду и его частичные суммы остаются ограниченными, почленное интегрирование на любом конечном отрезке допустимо. Ввиду 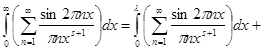 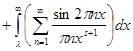 для любого для любого 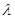 , остаётся доказать, что , остаётся доказать, что 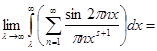 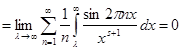 при при 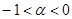 . Но интегрируя внутренний интеграл по частям имеем . Но интегрируя внутренний интеграл по частям имеем 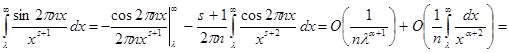
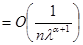 . Отсюда без труда получается наше утверждение. . Отсюда без труда получается наше утверждение.
Функциональное уравнение дзета-функции (7) может быть записано многими способами. Например, заменим s
на 1-s
, получаем равносильное равенство
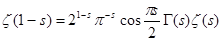 (8). Из него можно получить два небольших следствия. (8). Из него можно получить два небольших следствия.
Подставим в (8) вместо s
число 2m
, где m
– натуральное число. Имеем 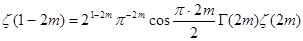 . По формуле (4) первой главы . По формуле (4) первой главы 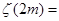 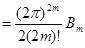 , а , а 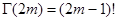 , поэтому , поэтому 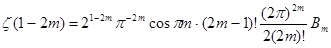 и произведя в правой части все сокращения, учитывая, что и произведя в правой части все сокращения, учитывая, что 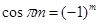 , получим , получим 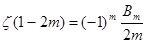 . .
Покажем ещё, что 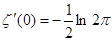 . Для этого прологарифмируем равенство (8): . Для этого прологарифмируем равенство (8): 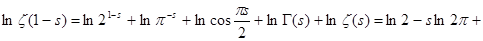 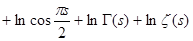 и результат продифференцируем и результат продифференцируем 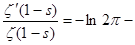 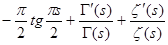 . В окрестности точки s
=1 . В окрестности точки s
=1 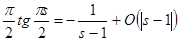 , , 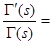 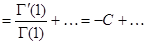 , , 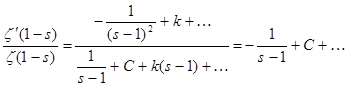 , где С
– постоянная Эйлера, а k
– произвольная постоянная. Следовательно, устремляя s
к единице, получим , где С
– постоянная Эйлера, а k
– произвольная постоянная. Следовательно, устремляя s
к единице, получим 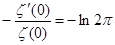 , то есть , то есть 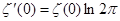 . Опять из формулы (4) главы 1 при k
=0 . Опять из формулы (4) главы 1 при k
=0 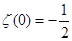 , значит, действительно, , значит, действительно, 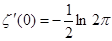 . .
Глава 3.
Как уже было сказано, дзета-функция Римана широко применяется в математическом анализе. Однако наиболее полно важность её выявляется в теории чисел, где она оказывает неоценимую помощь в изучении распределения простых чисел в натуральном ряду. К сожалению, рассказ о серьезных и нетривиальных применениях дзета-функции Римана выходит за рамки этой работы. Но чтобы хотя бы немного представить мощь этой функции, докажем с её помощью несколько интересных утверждений.
Например, известно, что простых чисел бесконечно много. Самое знаменитое элементарное доказательство принадлежит Евклиду. Оно состоит в следующем. Предположим, что существует конечное число простых чисел, обозначим их p
1
, p
2
, … , pn
. Рассмотрим число p
1
p
2
…
pn
+1, оно не делится ни на одно из простых и не совпадает ни с одним из них, то есть является простым числом, отличным от вышеуказанных, что противоречит предположению. Значит, количество простых чисел не может быть конечным.
Другое доказательство этого факта, использующее дзета-функцию, было дано Эйлером. Рассмотрим данное в первой главе равенство (5) при s
=1, получим 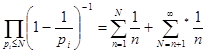 , отсюда , отсюда 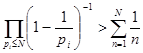 и ввиду расходимости гармонического ряда, имеем при и ввиду расходимости гармонического ряда, имеем при 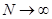
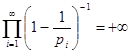 (1). Если бы количество простых чисел было конечным, то и это произведение имело конечное значение. Однако, полученный результат свидетельствует об обратном. Доказательство завершено. (1). Если бы количество простых чисел было конечным, то и это произведение имело конечное значение. Однако, полученный результат свидетельствует об обратном. Доказательство завершено.
Теперь перепишем (1) в виде 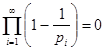 . Опираясь на теорему о сходимости бесконечного произведения, из расходимости предыдущего делаем вывод, что ряд . Опираясь на теорему о сходимости бесконечного произведения, из расходимости предыдущего делаем вывод, что ряд 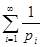 расходится. Это предложение даёт некоторую характеристику роста простых чисел. Подчеркнём, что оно гораздо сильнее утверждения о расходимости гармонического ряда, так как здесь речь идёт лишь о части его членов, тем более что в натуральном ряде имеются сколь угодно длинные промежутки без простых чисел, например: расходится. Это предложение даёт некоторую характеристику роста простых чисел. Подчеркнём, что оно гораздо сильнее утверждения о расходимости гармонического ряда, так как здесь речь идёт лишь о части его членов, тем более что в натуральном ряде имеются сколь угодно длинные промежутки без простых чисел, например: 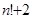 , , 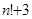 , … , , … , 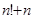 . .
Несмотря на свою простоту приведённые выше предложения важны в концептуальном плане, так как они начинают череду исследований всё более и более глубоких свойств ряда простых чисел, которая продолжается по сей день. Первоначально, основной целью изучения дзета-функции как раз и было исследование функции 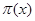 , то есть количества простых чисел не превосходящих x
. В качестве примера формулы, связывающей , то есть количества простых чисел не превосходящих x
. В качестве примера формулы, связывающей 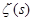 и и 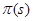 , мы сейчас получим равенство , мы сейчас получим равенство
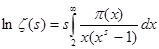 (2). (2).
Сначала воспользуемся разложением дзета-функции в произведение: 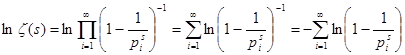 . Из логарифмического ряда . Из логарифмического ряда 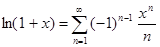 , учитывая, что , учитывая, что  , приходим к ряду , приходим к ряду  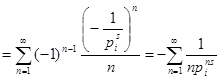 . Значит, . Значит, 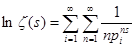 . .
Теперь вычислим интеграл в правой части (2). Так как при 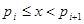 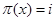 , то , то 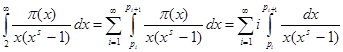 . Во внутреннем интеграле положим . Во внутреннем интеграле положим 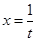 , тогда , тогда 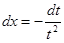 и и 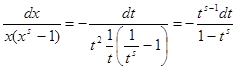 , отсюда , отсюда 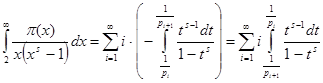 .В промежутке интегрирования .В промежутке интегрирования 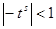 , поэтому верно разложение , поэтому верно разложение 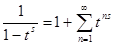 и и 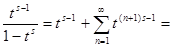 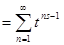 . Получаем . Получаем 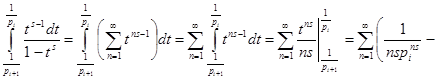  . Теперь . Теперь 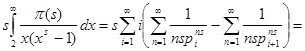 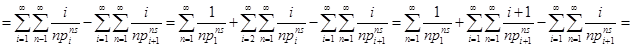 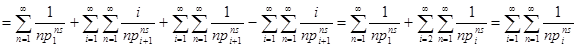 . Если сравнить полученное значение интеграла с рядом для . Если сравнить полученное значение интеграла с рядом для 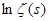 , то увидим, что они тождественны и равенство (2) доказано. , то увидим, что они тождественны и равенство (2) доказано.
Используем формулу (2) для доказательства одной очень серьёзной и важной теоремы, а именно получим асимптотический закон распределения простых чисел, то есть покажем, что 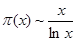 . .
В качестве исторической справки отмечу, что великий немецкий математик Карл Фридрих Гаусс эмпирически установил эту закономерность ещё в пятнадцатилетнем возрасте, когда ему подарили сборник математических таблиц, содержащий таблицу простых чисел и таблицу натуральных логарифмов.
Для доказательства возьмём формулу (2) и попытаемся разрешить это уравнение относительно 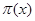 , то есть обратить интеграл. Сделаем это с помощью формулы обращения Меллина следующим образом. Пусть , то есть обратить интеграл. Сделаем это с помощью формулы обращения Меллина следующим образом. Пусть 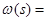 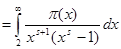 . Тогда . Тогда
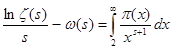 (3). Этот интеграл имеет нужную форму, а (3). Этот интеграл имеет нужную форму, а 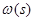 не повлияет на асимптотику не повлияет на асимптотику 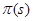 . Действительно, так как . Действительно, так как 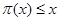 , интеграл для , интеграл для 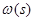 сходится равномерно в полуплоскости сходится равномерно в полуплоскости 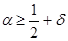 , что легко обнаруживается сравнением с интегралом , что легко обнаруживается сравнением с интегралом 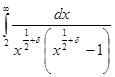 . Следовательно, . Следовательно, 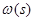 регулярна и ограничена в полуплоскости регулярна и ограничена в полуплоскости 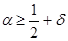 . То же самое справедливо и относительно . То же самое справедливо и относительно 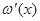 , так как , так как 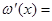 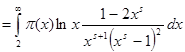 . .
Мы могли бы уже применить формулу Меллина, но тогда было бы весьма затруднительно выполнить интегрирование. Поэтому прежде преобразуем равенство (3) следующим образом. Дифференцируя по s
, получаем 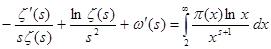 . Обозначим левую часть через . Обозначим левую часть через 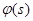 и положим и положим 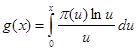 , , 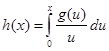 , ( , (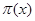 , , 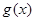 и и 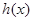 полагаем равными нулю при полагаем равными нулю при 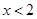 ). Тогда, интегрируя по частям, находим ). Тогда, интегрируя по частям, находим 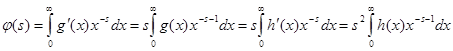 при при 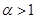 , или , или 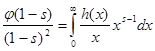 . .
Но 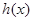 непрерывна и имеет ограниченную вариацию на любом конечном интервале, а так как непрерывна и имеет ограниченную вариацию на любом конечном интервале, а так как 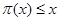 , то , то 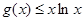 ( (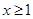 ) и ) и 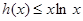 ( (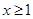 ). Следовательно, ). Следовательно, 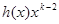 абсолютно интегрируема на абсолютно интегрируема на 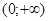 при при 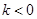 . Поэтому . Поэтому 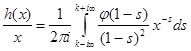 при при 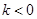 , или , или 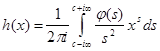 при при 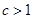 . Интеграл в правой части абсолютно сходится, так как . Интеграл в правой части абсолютно сходится, так как 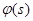 ограниченна при ограниченна при 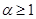 , вне некоторой окрестности точки , вне некоторой окрестности точки 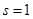 . В окрестности . В окрестности 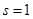 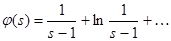 и можно положить и можно положить 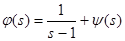 , где , где 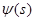 ограниченна при ограниченна при 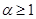 , , 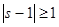 и имеет логарифмический порядок при и имеет логарифмический порядок при 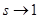 . Далее, . Далее, 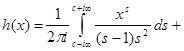 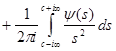 . Первый член равен сумме вычетов в особых точках, расположенных слева от прямой . Первый член равен сумме вычетов в особых точках, расположенных слева от прямой 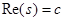 , то есть , то есть 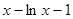 . Во втором члене можно положить . Во втором члене можно положить 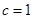 , так как , так как 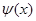 имеет при имеет при 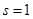 лишь логарифмическую особенность. Следовательно, лишь логарифмическую особенность. Следовательно, 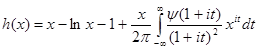 . Последний интеграл стремится к нулю при . Последний интеграл стремится к нулю при 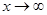 . Значит, . Значит,
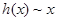 (4). (4).
Чтобы перейти обратно к 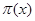 , используем следующую лемму. , используем следующую лемму.
Пусть 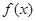 положительна и не убывает и пусть при положительна и не убывает и пусть при 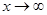 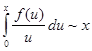 . Тогда . Тогда 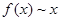 . .
Действительно, если 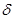 - данное положительное число, то - данное положительное число, то 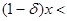 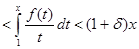 ( (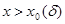 ). Отсюда получаем для любого ). Отсюда получаем для любого 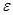 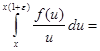 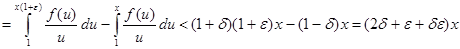 . Но так как . Но так как 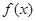 не убывает, то не убывает, то 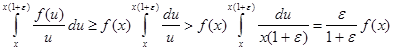 . Следовательно, . Следовательно, 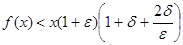 . Полагая, например, . Полагая, например, 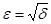 , получаем , получаем  . .
Аналогично, рассматривая 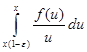 , получаем , получаем 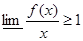 , значит , значит 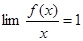 , что и требовалось доказать. , что и требовалось доказать.
Применяя лемму, из (4) имеем, что 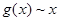 , , 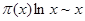 , поэтому , поэтому 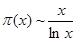 и теорема доказана. и теорема доказана.
Для ознакомления с более глубокими результатами теории дзета-функции Римана могу отослать заинтересованного читателя к прилагаемому списку использованной литературы.
Список использованной литературы.
1. Титчмарш Е.К. Теория дзета-функции Римана. Череповец, 2000 г.
2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том II. М.,1970 г.
3. Привалов И.И. Введение в теорию функций комплексного переменного. М.,1999 г.
4. Айерленд К., Роузен М. Классическое введение в современную теорию чисел. М.,1987 г.
5. Шафаревич З.А. Теория чисел. М.,1986г.
|