Введение
Целью выполнения данной работы является овладение статистическими методами при изучении социальных и экономических явлений и процессов и приобретение навыков использования статистической информации при принятии управленческих решений. Для этого студенты пройдут последовательно все этапы статистического исследования, начиная с самостоятельной организации и проведения статистического наблюдения и заканчивая всесторонним анализом полученных данных.
1. Проведение статистического наблюдения
Теоретико-методологический этап:
Для проведениястатистического наблюдения была выбрана участковая больница. Целью наблюдения является количество населения, принимаемые данным учреждением за месяц. Задачи – определить число людей, обращающихся в больницу, провести обследование качества обслуживания, выявит отношение к платному лечению. Единицей наблюдения, как уже было указано выше, – участковая больница. Территорией наблюдения будет населенный пункт Кезского района Удмуртской Республики поселок Кузьма. Время наблюдения – один месяц. Программа наблюдения состоит из исследования качества обслуживания населения, количества людей, обращающихся за помощью в больницу. Вид наблюдения по времени проведения является единовременное. По охвату единиц – несплошное, разновидность несплошного – монографическое наблюдения. Способом наблюдения является документальное наблюдения и опрос. Вид опроса выбран саморегистрация.
Организационный план:
Органом наблюдения является автор данной курсовой работы. Данные собираются в течение месяца. Подготовительной работой будет разработка формы представления результатов исследования, разработка опросных листов для проведения саморегистрации. Данные листы содержат вопросы и место для ответа, некоторые вопросы будут содержать возможные варианты ответа. С инструкциями по заполнению население будет знакомиться устно.
Примерные вопросы опросного листа:
1. Дата заполнения______________________________________________
2. Возраст______________________________________________________
3. Пол: М Ж (нужное подчеркнуть)
4. Социальное положение: работающий, пенсионер, учащийся, ребенок (нужное подчеркнуть)
Реклама

5. Место жительства______________________________________________
6. Удовлетворяет ли качество обслуживания? ________________________
7. Пожелания по качеству обслуживания ____________________________
_______________________________________________________________________________________________________________________________________________________________________________________
8. Отношение к платному лечению_________________________________
_______________________________________________________________________________________________________________________________________________________________________________________
9. Согласны ли вы будете, если за некоторые виды лечения будет взиматься плата. Если нет, почему________________________________ _______________________________________________________________________________________________________________________________________________________________________________________
10. Часто ли вы вызываете врача на дом? Отношение к обслуживанию _______________________________________________________________________________________________________________________________________________________________________________________
Контроль наблюдения необходим для выявления и устранения ошибок. В данном наблюдении может встретиться ошибка представительности. Для устранения этой ошибки проводится логический контроль. Ошибки будут исправляться лицом ответственным за наблюдение.
2. Группировка статистических данных
Численность занятых в экономике по занятиям в 2009 году[1]
(на конец ноября; тыс. чел.)
| Всего |
| Занятые в экономике –
всего |
70813
|
| в том числе: |
| руководители (представители) органов власти и управления всех уровней, включая руководителей организаций |
5273 |
| специалисты высшего уровня квалификации в области естественных и технических наук |
3468 |
| специалисты высшего уровня квалификации в области биологических, сельскохозяйственных наук и здравоохранения |
1567 |
| специалисты высшего уровня квалификации в области образования |
2944 |
| прочие специалисты высшего уровня квалификации |
5569 |
| специалисты среднего уровня квалификации физических и инженерных направлений деятельности |
2413 |
| специалисты среднего уровня квалификации и вспомогательный персонал естественных наук и здравоохранения |
2230 |
| специалисты среднего уровня квалификации в сфере образования |
1455 |
| средний персонал в области финансово-экономической, административной и социальной деятельности |
4341 |
| работники, занятые подготовкой информации, оформлением документации и учетом |
1379 |
| работники сферы обслуживания |
739 |
| работники сферы индивидуальных услуг и защиты граждан и собственности |
4489 |
продавцы, демонстраторы товаров,
натурщики и демонстраторы одежды |
5201 |
рабочие жилищно-коммунального
хозяйства |
217 |
| рабочие кино, – телестудий и родственных профессий, рабочие, занятые на рекламно-оформительских и реставрационных работах |
53 |
| квалифицированные работники сельского, лесного, охотничьего хозяйств, рыбоводства и рыболовства |
2477 |
| рабочие, занятые на горных, горно-капитальных и на строительно-монтажных и строительно-ремонтных работах |
3202 |
| рабочие металлообрабатывающей и машиностроительной промышленности |
4424 |
| рабочие, выполняющие прецизионные работы по металлу и другим материалам, рабочие художественных промыслов и других видов производств в художественной промышленности, рабочие полиграфического производства |
232 |
| профессии рабочих транспорта и связи |
933 |
| другие квалифицированные рабочие, занятые в промышленности, на транспорте, в связи, геологии и разведке недр |
1808 |
| операторы, аппаратчики и машинисты промышленных установок |
1065 |
| операторы, аппаратчики, машинисты промышленного оборудования и сборщики изделий |
836 |
| водители и машинисты подвижного оборудования |
6562 |
| неквалифицированные рабочие сферы обслуживания, жилищно-коммунального хозяйства, торговли и родственных видов деятельности |
472 |
| неквалифицированные рабочие сельского, лесного, охотничьего хозяйств, рыбоводства и рыболовства |
627 |
| неквалифицированные рабочие, занятые в промышленности, строительстве, на транспорте, в связи, геологии и разведке недр |
776 |
| профессии неквалифицированных рабочих, общие для всех видов экономической деятельности |
6063 |
Группировочным признаком является численность людей, занятых в экономике.
Так как признак количественный, следовательно, количество групп рассчитывается по формуле Стерджесса:
n
=1+3,322*lgN
,
где N
– объем совокупности.
Рассчитаем количество групп:
n
=1+3,322*lg28 = 5,821 ≈ 6, n
= 6
Определяем интервал группировки. Т.к. вариация исходных данных большая, то интервалы будут равные и закрытые, поэтому их величину определяем по формуле:
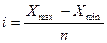 , ,
где Xmax
– наибольшее значение признака совокупности, Xmin
– наименьшее значение признака совокупности, n
– количество групп в группировке.
Рассчитаем интервалы группировки:
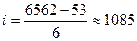
Единицы совокупности распределяются по группам
| Значение группировочного признака |
Количество единиц совокупности в группе |
| Хmin
+ i
= X1
* (Xmin
– X1
) |
| X1
+ i
= X2
* (X1
+X2
) |
| ………… |
| Xn-1
+ i
= Xn
* (Xn-1
– Xn
) |
| Итого |
N |
На основании полученных данных построим группировочную таблицу, учитывая, что округление интервала производилось в сторону увеличения, то нижняя граница последнего интервала будет больше чем наибольшее значение исходных данных:
Реклама

| Численность занятых в экономике |
Количество единиц в совокупности в группе |
| 53 – 1138 |
10 |
| 1138–2223 |
4 |
| 2223 – 3308 |
5 |
| 3308 – 4393 |
2 |
| 4393 – 5478 |
4 |
| 5478 – 6563 |
3 |
| Итого |
28 |

3. Расчет характеристик вариационного ряда
По полученной группировке построим вариационный ряд, рассчитаем показатели центра распределения и показатели вариации распределения. Т.к. группировка строилась по количественному признаку, то получим вариационный ряд. Он состоит из вариант (отдельные значения варьируемого признака в совокупности) и частот (количество единиц совокупности с данным значением признака).
К показателям центра распределения относятся средняя арифметическая, мода, медиана.
Средняя арифметическая рассчитывается по формуле:
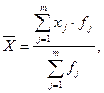
где m
– количество групп; xj
– варианты; fj
– частоты.
В интервальных рядах вместо вариант xj
используется середина интервала 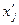 .
.
Найдем середину каждого из интервалов. Она находится по формуле:
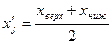 , ,
где x
верх
– верхняя граница интервала; x
ниж
– нижняя граница интервала.
Рассчитаем середину каждого интервала:
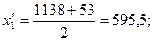 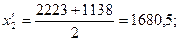 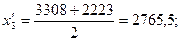 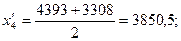 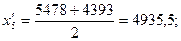 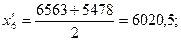
Рассчитаем среднюю арифметическую:
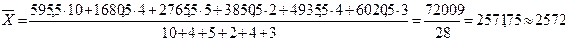
Таким образом, 2572 тыс. чел. – наиболее характерное значение численности населения, занятого в экономике.
Следующим показателем центра распределения является мода. В интервальных рядах по наибольшей частоте определяется модальный интервал, а затем рассчитывается мода по формуле:
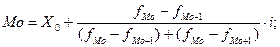
где X
0
- нижняя граница модального интервала; f
Mo –
частота модального интервала; f
Mo-1 –
частота предмодального интервала; f
Mo+1 –
частота послемодального интервала; i
– величина модального интервала.
Модальным интервалом является первая группа в группировочной таблице. Рассчитаем моду:
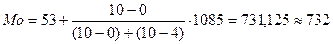
Таким образом, значение 505 тыс. чел. – наиболее часто встречаемое среди занятых в экономике.
Далее находим медиану. В интервальных рядах медиана равна варианте, накопленная частота которой больше либо равна половине объема совокупности (f
/
Me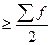 ). Накопленная частота (f
/)
в каждой группе рассчитывается сложением частоты в своей группе с частотами всех предыдущих групп. Медиана находится по формуле:
). Накопленная частота (f
/)
в каждой группе рассчитывается сложением частоты в своей группе с частотами всех предыдущих групп. Медиана находится по формуле:
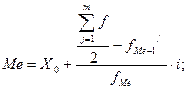
где X
0 –
нижняя граница медианного интервала; f
Me-1
/
–
накопленная частота предмедианного интервала; f
Me –
частота медианного интервала; i
– величина медианного интервала.
Половина объема совокупности равна 14 (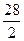 ). Медианным интервалом является вторая группа, т. к. ее накопленная частота равна 14. Теперь рассчитаем медиану: ). Медианным интервалом является вторая группа, т. к. ее накопленная частота равна 14. Теперь рассчитаем медиану:
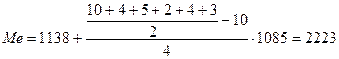
Половина из обследованных признаков меньше 2223 тыс. чел., а другая половина больше.
Теперь рассчитаем показатели центра распределения. К ним относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия, коэффициент вариации.
Размах вариации рассчитывается по формуле:
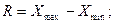
где 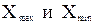 – наибольшее и наименьшее значения признака в совокупности. – наибольшее и наименьшее значения признака в совокупности.
Рассчитаем размах вариации:
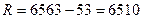
Среднее линейное отклонение рассчитывается как средняя арифметическая из модулей отклонений вариант от средней. Т.к. данные сгруппированы, то рассчитывается среднее линейное отклонение взвешенное:
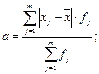
где xj
– варианты;f
j
– частоты; 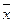 – среднее арифметическое. – среднее арифметическое.
Рассчитаем среднее линейное отклонение взвешенное:
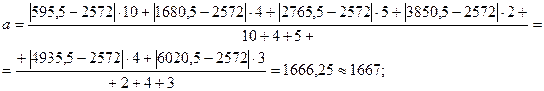
Среднее квадратическое отклонение рассчитывается как корень из средней арифметической квадратов отклонений от средней. По сгруппированным данным рассчитывается среднее квадратическое отклонение взвешенное:
 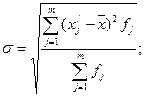
где m
– количество групп; x
/
j
– середина j
-го интервала; 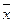 - средняя арифметическая; f
j
– частота j
-го интервала. - средняя арифметическая; f
j
– частота j
-го интервала.
Рассчитаем седнее квадратическое отклонение взвешенное:
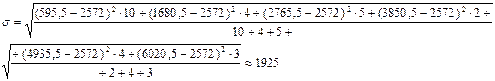
На 1667 и на 1925 тыс. чел. в среднем отличаются отдельные значения совокупности от средней численности занятых в экономике.
Взвешенная дисперсия рассчитывается по формуле:
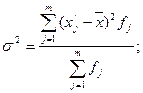
где 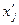 – середина интервала; – середина интервала; 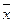 – среднее арифметическое;f
j
– частоты. – среднее арифметическое;f
j
– частоты.
Рассчитаем взвешенную дисперсию:
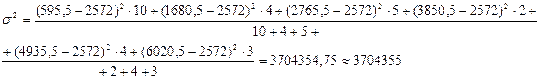
Найдем типичность средней величины через коэффициент вариации:
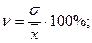
где 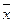 - средняя арифметическая; - средняя арифметическая; 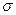 - среднее квадратическое отклонение. - среднее квадратическое отклонение.
Рассчитаем данный показатель:
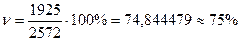
Так как коэффициент > 40%, следовательно, средняя нетипична, а исследуемая совокупность неоднородна.
4. Анализ связи между признаками по аналитической группировке
Денежные доходы и потребительские расходы в расчете на душу населения(рублей)
| Февраль 2009 г.1)
|
| Денежные доходы
|
Потребительские расходы
|
| Российская Федерация
|
14895,6
|
10290,3
|
| Центральный федеральный округ
|
20480,7
|
13519,9
|
| Белгородская область |
11930,2 |
7776,6 |
| Брянская область |
10430,6 |
7665,4 |
| Владимирская область |
9643,7 |
6154,2 |
| Воронежская область |
10188,7 |
7243,6 |
| Ивановская область |
8573,7 |
6059,9 |
| Калужская область |
12061,2 |
8413,0 |
| Костромская область |
10044,1 |
5775,5 |
| Курская область |
11145,3 |
7992,8 |
| Липецкая область |
11829,3 |
8547,9 |
| Московская область |
18288,0 |
12725,4 |
| Орловская область |
9177,9 |
6387,1 |
| Рязанская область |
9407,0 |
7030,9 |
| Смоленская область |
12416,5 |
7872,3 |
| Тамбовская область |
10240,3 |
7579,6 |
| Тверская область |
10772,9 |
8179,3 |
| Тульская область |
12497,5 |
8157,2 |
| Ярославская область |
11723,8 |
7716,2 |
| г. Москва |
40215,5 |
25492,4 |
| Приволжский федеральный округ
|
12130,1
|
8610,7
|
| Республика Башкортостан |
12213,3 |
9015,1 |
| Республика Марий Эл |
7777,3 |
5931,2 |
| Республика Мордовия |
7942,8 |
4948,6 |
| Республика Татарстан |
14693,7 |
11033,6 |
| Удмуртская Республика |
9668,8 |
6451,2 |
| Чувашская Республика |
8169,8 |
5769,5 |
| Пермский край |
15717,9 |
10835,8 |
| Кировская область |
9487,0 |
6008,8 |
| Нижегородская область |
12436,3 |
8925,0 |
| Оренбургская область |
10637,7 |
6664,8 |
| Пензенская область |
9741,3 |
6816,3 |
| Самарская область |
17697,0 |
12743,2 |
| Саратовская область |
8996,3 |
6150,0 |
| Ульяновская область |
8439,6 |
6672,2 |
| Дальневосточный федеральный округ
|
15262,8
|
9585,2
|
| Республика Саха (Якутия) |
17683,6 |
10509,0 |
| Камчатский край |
20510,9 |
9693,1 |
| Приморский край |
12149,9 |
8507,0 |
| Хабаровский край |
14877,6 |
9919,9 |
| Амурская область |
13400,5 |
6999,1 |
| Магаданская область |
20072,3 |
10176,7 |
| Сахалинская область |
22901,2 |
16124,3 |
| Еврейская авт. область |
11426,1 |
7158,4 |
| Чукотский авт. округ |
20066,4 |
9272,8 |
По имеющимся данным определим признак-фактор и признак-результат. Признак-фактор – денежные доходы, признак-результат – потребительские расходы. Построим группировку по признаку-фактору. Для этого определим количество групп и величину интервалов по вышеприведенным формулам.
Количество групп возьмем равной 5
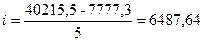
На основании полученных данных построим группировочную таблицу:
| Денежные доходы населения |
Количество в группе |
| 7777,3 – 14264,94 |
30 |
| 14264,94 – 20752,58 |
9 |
| 20752,58 – 27240,22 |
1 |
| 27240,22 – 33727,86 |
0 |
| 33727,86 – 40215,5 |
1 |
| Итого |
41 |
В каждой группе рассчитаем среднее значение результативного признака как простую среднюю арифметическую из значений результативного признака у всех единиц совокупности, входящих в данную группу. Она рассчитывается по формуле:
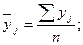
где yj
– значение результативного признака в группе; n
– количество единиц в группе.
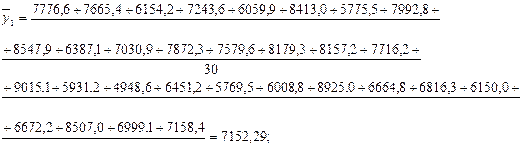
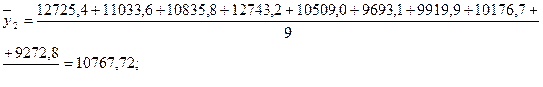

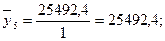
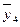 не будет, т. к. данное значение признака-фактора отсутствует. не будет, т. к. данное значение признака-фактора отсутствует.
Аналитическая группировочная таблица
| Интервалы признака-фактора |
Количество единиц в группе |
Среднее значение результативного признака по группам |
| 7777,3 – 14264,94 |
30 |
7152,29 |
| 14264,94 – 20752,58 |
9 |
10767,73 |
| 20752,58 – 27240,22 |
1 |
16124,3 |
| 27240,22 – 33727,86 |
0 |
0 |
| 33727,86 – 40215,5 |
1 |
25492,4 |
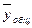 |
41 |
11907,34 |
По полученным данным проведем дисперсионный анализ и определим характер связи.
В анализе рассчитываются три вида дисперсии: межгрупповая, средняя внутригрупповая, общая.
Межгрупповая дисперсия рассчитывается по формуле:
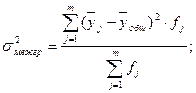
где 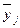 – групповые средние результативного признака; fj
– групповые частоты; – групповые средние результативного признака; fj
– групповые частоты; 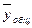 – общая средняя результативного признака в совокупности. – общая средняя результативного признака в совокупности.
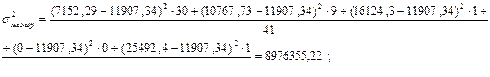
8976355,22 рублей – вариация потребительских расходов под влиянием денежных доходов.
Для расчета средней внутригрупповой дисперсии сначала находится внутригрупповые дисперсии по каждой группе аналитической группировки:
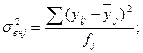
где yij
– отдельные значения результативного признака в j
-й группе; 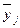 – среднее значение результативного признака в j
-й группе; fj
– частота в j
-й группе. – среднее значение результативного признака в j
-й группе; fj
– частота в j
-й группе.
Рассчитаем внутригрупповые дисперсии:
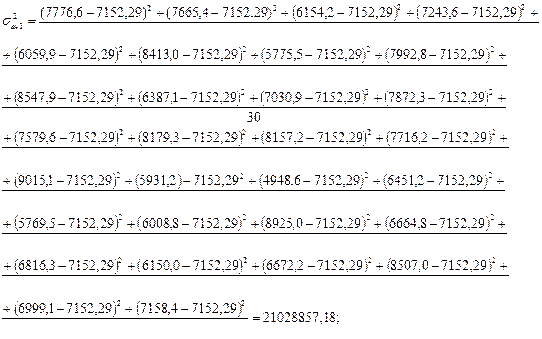
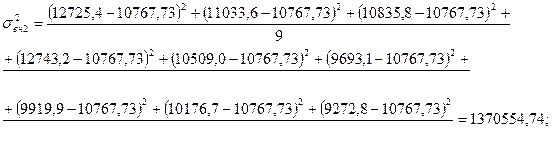 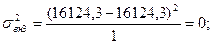
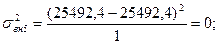
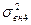 – отсутствует, т. к. нет результативного признака в 4-ой группе. – отсутствует, т. к. нет результативного признака в 4-ой группе.
Средняя внутригрупповая дисперсия:
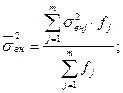
где 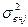 – внутригрупповая дисперсия по каждой группе; – внутригрупповая дисперсия по каждой группе; 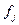 – частота в j
-й группе. – частота в j
-й группе.
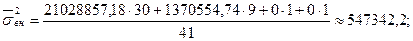
547342,2 – случайная вариация потребительских расходов, возникающая под влиянием денежных доходов.
Общая дисперсия находится по формуле:
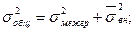
где 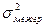 – межгрупповая дисперсия; – межгрупповая дисперсия; 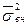 – внутригрупповая дисперсия. – внутригрупповая дисперсия.
Рассчитаем общую дисперсию:
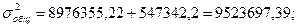
Мерой тесноты связи между результативным и факторным признаками является коэффициент детерминации:
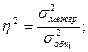
Рассчитаем коэффициент детерминации:
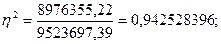
0,94 – эта часть общей вариации потребительских расходов объясняется денежными доходами.
Эмпирическое корреляционное отношение показывает тесноту связи:
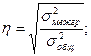
Рассчитаем данный показатель:
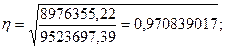
Определяем показатель силы связи:
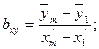
где 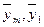 – средние значения результативного признака в первой и последней группах; – средние значения результативного признака в первой и последней группах; 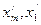 – середины интервалов факторного признака в первой и последней группах. – середины интервалов факторного признака в первой и последней группах.
Для этого определим середины первой и последней групп, по вышеприведенным формулам:
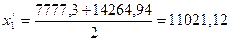
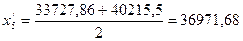
Рассчитаем силу связи:
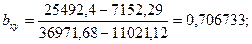
Из данного показателя следует, что сила связи прямая, т.е. при увеличении денежных доходов на 1 рубль происходит увеличение потребительских расходов на 0,71 рубль.
5. Корреляционно-регрессионный анализ
Данный анализ проведем на основании данных, приведенных в задании 4.4.
| Денежные доходы
|
Потребительские расходы
|
| Белгородская область |
11930,2 |
7776,6 |
| Брянская область |
10430,6 |
7665,4 |
| Владимирская область |
9643,7 |
6154,2 |
| Воронежская область |
10188,7 |
7243,6 |
| Ивановская область |
8573,7 |
6059,9 |
| Калужская область |
12061,2 |
8413,0 |
| Костромская область |
10044,1 |
5775,5 |
| Курская область |
11145,3 |
7992,8 |
| Липецкая область |
11829,3 |
8547,9 |
| Московская область |
18288,0 |
12725,4 |
| Орловская область |
9177,9 |
6387,1 |
| Рязанская область |
9407,0 |
7030,9 |
| Смоленская область |
12416,5 |
7872,3 |
| Тамбовская область |
10240,3 |
7579,6 |
| Тверская область |
10772,9 |
8179,3 |
| Тульская область |
12497,5 |
8157,2 |
| Ярославская область |
11723,8 |
7716,2 |
| г. Москва |
40215,5 |
25492,4 |
| Республика Башкортостан |
12213,3 |
9015,1 |
| Республика Марий Эл |
7777,3 |
5931,2 |
| Республика Мордовия |
7942,8 |
4948,6 |
| Республика Татарстан |
14693,7 |
11033,6 |
| Удмуртская Республика |
9668,8 |
6451,2 |
| Чувашская Республика |
8169,8 |
5769,5 |
| Пермский край |
15717,9 |
10835,8 |
| Кировская область |
9487,0 |
6008,8 |
| Нижегородская область |
12436,3 |
8925,0 |
| Оренбургская область |
10637,7 |
6664,8 |
| Пензенская область |
9741,3 |
6816,3 |
| Самарская область |
17697,0 |
12743,2 |
| Саратовская область |
8996,3 |
6150,0 |
| Ульяновская область |
8439,6 |
6672,2 |
| Республика Саха (Якутия) |
17683,6 |
10509,0 |
| Камчатский край |
20510,9 |
9693,1 |
| Приморский край |
12149,9 |
8507,0 |
| Хабаровский край |
14877,6 |
9919,9 |
| Амурская область |
13400,5 |
6999,1 |
| Магаданская область |
20072,3 |
10176,7 |
| Сахалинская область |
22901,2 |
16124,3 |
| Еврейская авт. область |
11426,1 |
7158,4 |
| Чукотский авт. округ |
20066,4 |
9272,8 |
Изобразим связь между данными признаками графически:
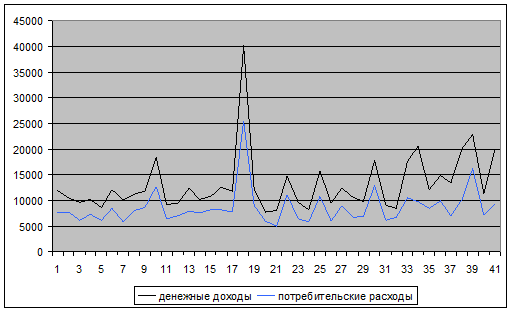
Исследуется парная линейная корреляция:
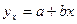
Рассчитаем параметры a
иb
:
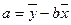
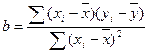
Промежуточные расчеты приводим в таблице:
Денеж-ные доходы
(х)
|
Потреби-тельские расходы
(у)
|
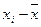 |
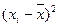 |
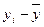 |
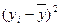 |
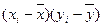 |
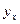 |
| 1 |
11930,2 |
7776,6 |
-1173,8 |
1377806,44 |
-835,4 |
697893,16 |
980592,52 |
7938 |
| 2 |
10430,6 |
7665,4 |
-2673,4 |
7147067,56 |
-946,6 |
896051,56 |
2530640,44 |
7077 |
| 3 |
9643,7 |
6154,2 |
-3460,3 |
11973676,09 |
-2457,8 |
6040780,84 |
8504725,34 |
6625 |
| 4 |
10188,7 |
7243,6 |
-2915,3 |
8498974,09 |
-1368,4 |
1872518,56 |
3989296,52 |
6938 |
| 5 |
8573,7 |
6059,9 |
-4530,3 |
20523618,09 |
-2552,1 |
6513214,41 |
11561778,63 |
6010 |
| 6 |
12061,2 |
8413 |
-1042,8 |
1087431,84 |
-199 |
39601 |
207517,2 |
8013 |
| 7 |
10044,1 |
5775,5 |
-3059,9 |
9362988,01 |
-2836,5 |
8045732,25 |
8679406,35 |
6855 |
| 8 |
11145,3 |
7992,8 |
-1958,7 |
3836505,69 |
-619,2 |
383408,64 |
1212827,04 |
7487 |
| 9 |
11829,3 |
8547,9 |
-1274,7 |
1624860,09 |
-64,1 |
4108,81 |
81708,27 |
7880 |
| 10 |
18288 |
12725,4 |
5184 |
26873856 |
4113,4 |
16920079,56 |
21323865,6 |
11589 |
| 11 |
9177,9 |
6387,1 |
-3926,1 |
15414261,21 |
-2224,9 |
4950180,01 |
8735179,89 |
6357 |
| 12 |
9407 |
7030,9 |
-3697 |
13667809 |
-1581,1 |
2499877,21 |
5845326,7 |
6489 |
| 13 |
12416,5 |
7872,3 |
-687,5 |
472656,25 |
-739,7 |
547156,09 |
508543,75 |
8217 |
| 14 |
10240,3 |
7579,6 |
-2863,7 |
8200977,69 |
-1032,4 |
1065849,76 |
2956483,88 |
6967 |
| 15 |
10772,9 |
8179,3 |
-2331,1 |
5434027,21 |
-432,7 |
187229,29 |
1008666,97 |
7273 |
| 16 |
12497,5 |
8157,2 |
-606,5 |
367842,25 |
-454,8 |
206843,04 |
275836,2 |
8264 |
| 17 |
11723,8 |
7716,2 |
-1380,2 |
1904952,04 |
-895,8 |
802457,64 |
1236383,16 |
7819 |
| 18 |
40215,5 |
25492,4 |
27111,5 |
735033432,3 |
16880,4 |
284947904,2 |
457652964,6 |
24182 |
| 19 |
12213,3 |
9015,1 |
-890,7 |
793346,49 |
403,1 |
162489,61 |
-359041,17 |
8100 |
| 20 |
7777,3 |
5931,2 |
-5326,7 |
28373732,89 |
-2680,8 |
7186688,64 |
14279817,36 |
5553 |
| 21 |
7942,8 |
4948,6 |
-5161,2 |
26637985,44 |
-3663,4 |
13420499,56 |
18907540,08 |
5648 |
| 22 |
14693,7 |
11033,6 |
1589,7 |
2527146,09 |
2421,6 |
5864146,56 |
3849617,52 |
9525 |
| 23 |
9668,8 |
6451,2 |
-3435,2 |
11800599,04 |
-2160,8 |
4669056,64 |
7422780,16 |
6639 |
| 24 |
8169,8 |
5769,5 |
-4934,2 |
24346329,64 |
-2842,5 |
8079806,25 |
14025463,5 |
5778 |
| 25 |
15717,9 |
10835,8 |
2613,9 |
6832473,21 |
2223,8 |
4945286,44 |
5812790,82 |
10113 |
| 26 |
9487 |
6008,8 |
-3617 |
13082689 |
-2603,2 |
6776650,24 |
9415774,4 |
6535 |
| 27 |
12436,3 |
8925 |
-667,7 |
445823,29 |
313 |
97969 |
-208990,1 |
8229 |
| 28 |
10637,7 |
6664,8 |
-2466,3 |
6082635,69 |
-1947,2 |
3791587,84 |
4802379,36 |
7196 |
| 29 |
9741,3 |
6816,3 |
-3362,7 |
11307751,29 |
-1795,7 |
3224538,49 |
6038400,39 |
6681 |
| 30 |
17697 |
12743,2 |
4593 |
21095649 |
4131,2 |
17066813,44 |
18974601,6 |
11250 |
| 31 |
8996,3 |
6150 |
-4107,7 |
16873199,29 |
-2462 |
6061444 |
10113157,4 |
6253 |
| 32 |
8439,6 |
6672,2 |
-4664,4 |
21756627,36 |
-1939,8 |
3762824,04 |
9048003,12 |
5933 |
| 33 |
17683,6 |
10509 |
4579,6 |
20972736,16 |
1897 |
3598609 |
8687501,2 |
11242 |
| 34 |
20510,9 |
9693,1 |
7406,9 |
54862167,61 |
1081,1 |
1168777,21 |
8007599,59 |
12866 |
| 35 |
12149,9 |
8507 |
-954,1 |
910306,81 |
-105 |
11025 |
100180,5 |
8064 |
| 36 |
14877,6 |
9919,9 |
1773,6 |
3145656,96 |
1307,9 |
1710602,41 |
2319691,44 |
9631 |
| 37 |
13400,5 |
6999,1 |
296,5 |
87912,25 |
-1612,9 |
2601446,41 |
-478224,85 |
8782 |
| 38 |
20072,3 |
10176,7 |
6948,3 |
48278872,89 |
1564,7 |
2448286,09 |
10872007,01 |
12602 |
| 39 |
22901,2 |
16124,3 |
9797,2 |
95985127,84 |
7512,3 |
56434651,29 |
73599505,56 |
14238 |
| 40 |
11426,1 |
7158,4 |
-1677,9 |
2815348,41 |
-1453,6 |
2112952,96 |
2438995,44 |
7648 |
| 41 |
20066,4 |
9272,8 |
6942,4 |
48196917,76 |
660,8 |
436656,64 |
4587537,92 |
12599 |
| Итого |
537253,5 |
353094,9 |
1340013576 |
492253673,8 |
769548829,3 |
| Сред-нее |
13104 |
8612 |
Рассчитаем параметры уравнения:

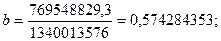
Составим уравнение парной линейной корреляции:
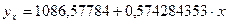
Составим график теоретического значения потребительских расходов:
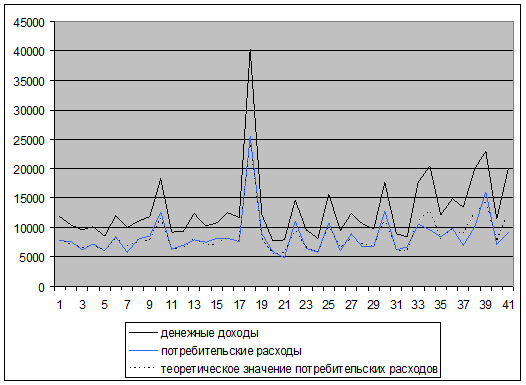
Найдем тесноту связи между денежными доходами и потребительскими расходами:
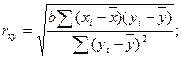
Рассчитаем данный показатель:
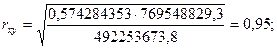
Рассчитаем коэффициент детерминации:
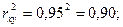
Т.о. связь между потребительскими расходами и денежными доходами весьма тесная, изменение потребительских расходов на 90% зависит от денежных доходов населения.
6. Анализ рядов динамики
Численность постоянного населения на 1 января, человек, на 1 января
| 2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
| Удмуртская Республика |
1601409 |
1595571 |
1588054 |
1578187 |
1568176 |
1560260 |
1552759 |
1544426 |
1537858 |
1532736 |
По приведенным данным рассчитаем основные характеристики интервального ряда динамики:
наблюдение статистический группировка вариационный
| Характеристики ряда динамики |
Цепные |
Базисные |
| 1. Абсолютный прирост |
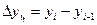 |
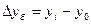 |
| 2. Темп роста |
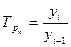 |
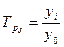 |
| 3. Темп прироста |
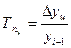 |
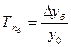 |
Средние характеристики интервального ряда динамики определяется по формуле:
Средний уровень ряда:
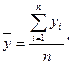 , ,
где 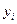 - значениеi
-го уровня; n
– количество уровней в ряду динамики. - значениеi
-го уровня; n
– количество уровней в ряду динамики.
По данным формулам рассчитаем показатели:
Абсолютный прирост цепной:
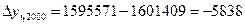 ; ;
Абсолютный прирост базисный:
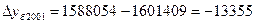 ; ;
Темп роста цепной:
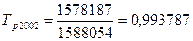 ; ;
Темп роста базисный:
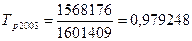 ; ;
Темп прироста цепной:
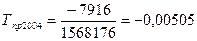 ; ;
Темп прироста базисный:
 . .
Аналогично рассчитываются показатели за другие года. При этом, цепные показатели имеют переменную базу сравнения, а базисные – постоянную – 2001 года.
В таблице приведены рассчитанные показатели:
| Абсолютный прирост |
Темп роста |
Темп прироста |
| Цепные |
Базисные |
Цепной |
Базисный |
Цепной |
Базисный |
| 2001
|
1601409 |
| 2002
|
1595571 |
-5838 |
-5838 |
0,996354 |
0,996354 |
-0,00365 |
-0,00365 |
| 2003
|
1588054 |
-7517 |
-13355 |
0,995289 |
0,99166 |
-0,00471 |
-0,00834 |
| 2004
|
1578187 |
-9867 |
-23222 |
0,993787 |
0,985499 |
-0,00621 |
-0,0145 |
| 2005
|
1568176 |
-10011 |
-33233 |
0,993657 |
0,979248 |
-0,00634 |
-0,02075 |
| 2006
|
1560260 |
-7916 |
-41149 |
0,994952 |
0,974305 |
-0,00505 |
-0,0257 |
| 2007
|
1552759 |
-7501 |
-48650 |
0,995192 |
0,969621 |
-0,00481 |
-0,03038 |
| 2008
|
1544426 |
-8333 |
-56983 |
0,994633 |
0,964417 |
-0,00537 |
-0,03558 |
| 2009
|
1537858 |
-6568 |
-63551 |
0,995747 |
0,960316 |
-0,00425 |
-0,03968 |
| 2010
|
1532736 |
-5122 |
-68673 |
0,996669 |
0,957117 |
-0,00333 |
-0,04288 |
Далее найдем средний уровень интервального ряда по формуле:
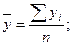
где yi
– уровни ряда; n
– количество уровней в ряду.
Рассчитаем данный показатель:
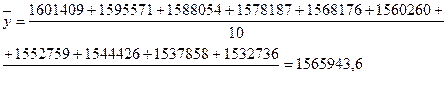
Проанализировав полученные данные можно сказать, что численность постоянного населения в Удмуртии на протяжении 10 лет постепенно снижается. По сравнению с 2001 годом, в 2010 году уменьшение численности достигло на данный момент наибольшего значения – 68673 человека. Темп роста цепной показывает, на сколько изменилась численность населения по сравнению с предыдущим годом. В среднем численность уменьшается на 0,05 долей. А уменьшение данного показателя по сравнению с 2001 годом варьируется от 0,04 до 0,5. В данном случае цепной темп прироста показывает уменьшение абсолютного прироста относительно численности населения в разные годы (от 0,006 до 0,003). А базисный – относительно 2001 года. Это уменьшение варьируется от 0,006 до 0,09.
Произведем сглаживание ряда с помощью скользящей средней. Для этого установим звенья скользящей средней – 3. Теперь рассчитаем средние уровни в каждом звене по формулам:
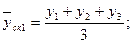 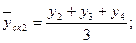 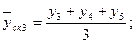 и т.д. и т.д.
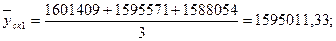
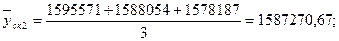
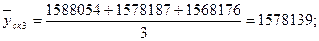
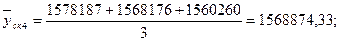
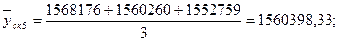
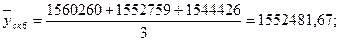
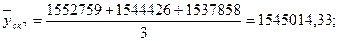
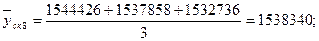
Т.к. в звене нечетное количество элементов, то можно определить тенденцию по ряду скользящих средних. Для этого построим график и нанесем на него полученный тренд.
Произведем сглаживание ряда динамики с помощью аналитического выравнивания по адекватной функции. В данном методе тенденция рассматривается как функция от времени: 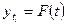 . Выберем линейную функцию: . Выберем линейную функцию: 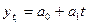 . Параметры а0,
а1
находятся по формулам: . Параметры а0,
а1
находятся по формулам:
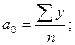 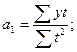
Промежуточные расчеты приведены в таблице:
| Год |
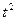 |
Численность |
ty
|
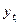 |
| 2001
|
3996001 |
1601409 |
3201216591 |
3128333,793 |
| 2002
|
4000000 |
1595571 |
3191142002 |
3129115,379 |
| 2003
|
4004001 |
1588054 |
3177696054 |
3129896,965 |
| 2004
|
4008004 |
1578187 |
3159530374 |
3130678,551 |
| 2005
|
4012009 |
1568176 |
3141056528 |
3131460,137 |
| 2006
|
4016016 |
1560260 |
3126761040 |
3132241,723 |
| 2007
|
4020045 |
1552759 |
3113281795 |
3133023,309 |
| 2008
|
4024036 |
1544426 |
3098118556 |
3133804,894 |
| 2009
|
4028049 |
1537858 |
3086481006 |
3134586,48 |
| 2010
|
4032064 |
1532736 |
3077733888 |
3135368,066 |
| Итого |
40140205 |
15659436 |
31373017832 |
Теперь рассчитаем необходимые параметры:
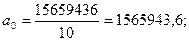 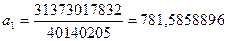
Подставив полученные параметры в уравнение функции, найдем, тенденцию и представим ее на графике:
Из проведенного анализа можно сделать вывод о том, что численность населения имеет тенденцию к постепенному увеличению.
7. Индексы
Динамика реализации овощей на рынках города в 2010 году
№
п/п
|
Наименование товара |
Январь |
Февраль |
Март |
Апрель |
Май |
| Продано товаров, ц |
Оборот, тыс. руб. |
Продано товаров, ц |
Оборот, тыс. руб. |
Продано товаров, ц |
Оборот, тыс. руб. |
Продано товаров, ц |
Оборот, тыс. руб. |
Продано товаров, ц |
Оборот, тыс. руб. |
| 1. |
Картофель |
299, 8 |
40,5 |
269,0 |
40,4 |
246,1 |
36,9 |
249,4 |
37,4 |
238,0 |
32,1 |
| 2. |
Капуста |
26,3 |
10,6 |
35,4 |
17,7 |
29,0 |
14,5 |
40,5 |
20,3 |
35,0 |
13,7 |
| 3. |
Лук репчатый |
75,4 |
30,2 |
82,7 |
49,6 |
57,8 |
40,5 |
65,4 |
45,2 |
45,8 |
29,8 |
| 4. |
Свёкла |
31,9 |
8,0 |
35,5 |
10,1 |
27,4 |
8,3 |
36,4 |
12,7 |
25,5 |
8,9 |
| 5. |
Морковь |
22,1 |
14,8 |
29,4 |
25,0 |
22,6 |
22,2 |
28,8 |
28,9 |
22,7 |
22,7 |
Рассчитаем цепные индексы, проверим правильность расчетов индексов, используя их взаимосвязь, рассчитаем сводные индексы цен и физических объемов с постоянными и переменными весами, сделаем выводы об изменении исследуемых показателей.
Индивидуальные цепные индексы рассчитываются по формулам:
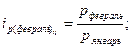 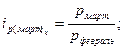 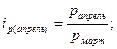 и т.д. и т.д.
Для проверки правильности расчета найдем индивидуальные базисные индексы цены:
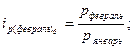 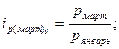 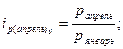
Приведем пример расчета по одному из этих показателей, остальные приведем в таблице:
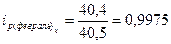
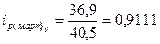
| Февраль |
Март |
Апрель |
Май |
Проверка |
| Индексы цепные
|
| Картофель |
0,9975 |
0,9134 |
1,0136 |
0,8583 |
0,7926 |
| Капуста |
1,6698 |
0,8192 |
1,4 |
0,6749 |
1,2925 |
| Лук репчатый |
1,6424 |
0,8165 |
1,1161 |
0,6593 |
0,9868 |
| Свёкла |
1,2625 |
0,8218 |
1,5301 |
0,7008 |
1,1125 |
| Морковь |
1,6892 |
0,888 |
1,3018 |
0,7855 |
1,5338 |
| Индексы базисные
|
| Картофель |
0,9975 |
0,9111 |
0,9235 |
0,7926 |
| Капуста |
1,6698 |
1,3679 |
1,9151 |
1,2925 |
| Лук репчатый |
1,6424 |
1,3411 |
1,4967 |
0,9868 |
| Свёкла |
1,2625 |
1,0375 |
1,5875 |
1,1125 |
| Морковь |
1,6892 |
1,5 |
1,9527 |
1,5338 |
Проверка основана на связи индексов: произведение цепных индексов дает базисный индекс последнего периода.
Рассчитаем сводные индексы цен и физического объема.
Общие цепные индексы цены:
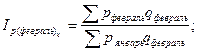  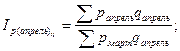 и т.д. и т.д.
Общие базисные индексы цены:
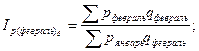  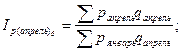 и т.д. и т.д.
Общие цепные индексы физического объема:
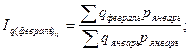 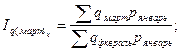 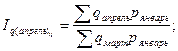 и т.д. и т.д.
Общие базисные индексы физического объема:
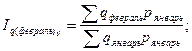  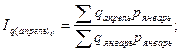
Рассчитаем по одному из индексов, а остальные приведем в таблице:
| Картофель |
Капуста |
Лук репчатый |
Свёкла |
Морковь |
сумма |
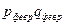 |
10867,6 |
626,58 |
4101,92 |
358,55 |
735 |
16689,65 |
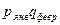 |
10894,5 |
375,24 |
2497,54 |
284 |
435,12 |
14486,4 |
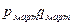 |
9081,09 |
420,5 |
2340,9 |
227,42 |
501,72 |
12571,63 |
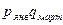 |
9967,05 |
307,4 |
1745,56 |
219,2 |
334,48 |
12573,69 |
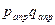 |
9327,56 |
822,15 |
2956,08 |
462,28 |
832,32 |
14400,39 |
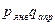 |
10100,7 |
429,3 |
1975,08 |
291,2 |
426,24 |
13222,52 |
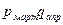 |
9202,86 |
587,25 |
2648,7 |
302,12 |
639,36 |
13380,29 |
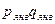 |
12141,9 |
3177,88 |
9053,96 |
2398,4 |
4437,04 |
31209,18 |
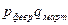 |
9942,44 |
513,3 |
2866,88 |
276,74 |
565 |
14164,36 |
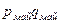 |
7639,8 |
479,5 |
1364,84 |
226,95 |
515,29 |
10226,38 |
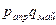 |
8901,2 |
710,5 |
2070,16 |
323,85 |
656,03 |
12661,74 |
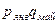 |
9639 |
371 |
1383,16 |
204 |
335,96 |
11933,12 |
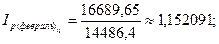
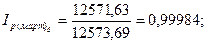
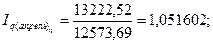
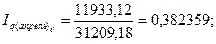
| февраль |
март |
апрель |
май |
| Индексы цены цепные |
1,152091 |
0,887554 |
1,076239 |
0,80766 |
| Индексы цены базисные |
1,152091 |
0,999836 |
1,089081 |
0,856975 |
| Индексы физического объема цепные |
0,464171 |
0,867965 |
1,051602 |
0,902485 |
| Индексы физического объема базисные |
0,464171 |
0,402884 |
0,423674 |
0,382359 |
Анализируя индивидуальные цепные индексы можно сделать следующие выводы. Цена на картофель в феврале уменьшилась на 0,25% по сравнению с ценами в январе. А цены на капусту, лук, свёклу, морковь растут на 68,98%, 64,24%, 26,25% и 68,92% соответственно. В марте цены, по сравнению с февральскими ценами, на данную продукцию уменьшились, в апреле снова поднялись в сравнении с мартом, а в мае снова упали.
Анализируя базисные индексы цен, можно сказать, что на картофель цена имеет тенденцию к снижению по сравнению с ценами января. На остальную сельскохозяйственную продукцию – к увеличению.
Общие цепные индексы цены показывают изменение стоимости товаров в данном месяце по сравнению с ценами предыдущего месяца и объемом продаж данного месяца. В феврале, например, стоимость товаров увеличилась на 15,21%, в марте уменьшилась на 11,24%, в апреле увеличилась на 7,62%, в мае снова снизилась на 11,23%.
Общие базисные индексы цены показывают изменение стоимости товаров в данном месяце по сравнению с ценами января и объемом продаж в данном месяце. Так, в феврале и апреле данный индекс увеличился на 15,21% и 8,92% соответственно, в марте и мае уменьшился на 0,02% и 14,3% соответственно.
Общие цепные индексы физического объема показывают изменение товарооборота в данном месяце и цены января по сравнению с ценами января и объемам продаж в предыдущем месяце. По данной таблице видно, что в феврале, марте и мае этот индекс уменьшился на 53,58%, 13,2% и 9,75% соответственно. А в апреле – увеличился на 5,16%.
Общие базисные индексы физического объема показывают изменение товарооборота в данном месяце и цены января по сравнению с ценами и объемом продаж в январе. Данный показатель на протяжении всех исследуемых месяцев уменьшаются на 53,58% в феврале, на 40,2% в марте, на 57,63% в апреле и 61,76% в мае.
Список использованной литературы
1. Методические указания по выполнению курсовой работы по дисциплине «Статистика» – Глазов, 2006. – 32 с.
2. www.gks.ru
[1]
По данным выборочного обследования населения по проблемам занятости. Данные приведены по основному или единственному месту работы.
Перечень группировок занятий приведен в соответствии с Общероссийским классификатором занятий.
|