| Содержание
1. Рассчитать трехфазное короткое замыкание в точке К-1 заданной схемы
1.1. Определить мгновенное значение апериодической составляющей тока КЗ при t=0,1 с.
2. Рассчитать однофазное короткое замыкание в точке К-2 заданной схемы.
2.1. Определить действующее значение периодической составляющей тока в точке К-2 для момента времени t=0,2 с. Построить векторные диаграммы токов и напряжений в месте несимметричного КЗ для заданного момента времени.
2.2. Определить действующее значение периодической составляющей тока КЗ в указанном сечении F-F и напряжения в указанной точке М для момента времени t=0,2 с и построить соответствующие векторные диаграммы.
Список использованной литературы
1.1. Определить мгновенное значение апериодической составляющей тока КЗ при t=0,1 с.
Используя результаты пунктов 1.1 и 1.2 приводим исходную схему (рис.1.1.1) к двух лучевому виду (рис. 1.3.1).
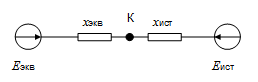
Рис. 1.1.1
Далее находим начальные значения периодических составляющих тока КЗ обоих лучей.
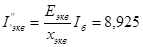 кА кА
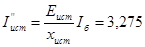 кА кА
Далее составим схему замещения, в которую все элементы вводятся своими активными сопротивлениями.
Данная схема замещения показана на рисунке 1.3.2:
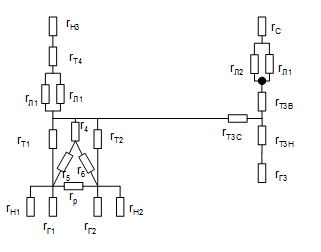
Рис. 1.1.2
В таблице 1.3.1 показаны параметры схемы замещения 1.3.2, которые были получены с помощью таблицы 1.1.1 и таблицы 5.3 [1, c.42]
Таблица 1.1.1
Параметры схемы замещения
| Элемент
|
Обозначение
|
Индуктивное сопротивление (о.е.м.)
|
Активное сопротивление (о.е.м.)
|
| Генератор Г-1
|
Г1
|
0,2
|
17
|
| Генератор Г-2
|
Г2
|
0,2
|
17
|
| Генератор Г-3
|
Г3
|
0,15
|
15
|
| Нагрузка Н-1
|
Н1
|
0,7
|
1,75
|
| Нагрузка Н-2
|
Н2
|
0,7
|
1,75
|
| Нагрузка Н-3
|
Н3
|
1
|
2,5
|
| Воздушная линия Л-1
|
Л1
|
0,2
|
0,8
|
| Воздушная линия Л-2
|
Л2
|
0,05
|
0,2
|
| Трансформатор Т-1
|
Т1
|
0,13
|
5,2
|
| Трансформатор Т-2
|
Т2
|
0,13
|
5,2
|
| Трансформатор Т-3
|
Т3В
|
0,09
|
3,6
|
| |
Т3С
|
0
|
0
|
| |
Т3Н
|
0,19
|
7,6
|
| Трансформатор Т-4
|
Т4
|
0,26
|
4,42
|
| Резистор
|
Р
|
0,0002
|
0,012
|
| Система
|
С
|
0,032
|
3,2
|
Далее преобразуем схему 1.3.2 к двух лучевому виду. Для начала «треугольник» 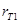 , , 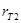 и и 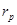 преобразовываем в «звезду»: преобразовываем в «звезду»:
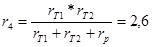
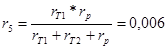
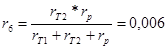
Схема после преобразования показана на рисунке 1.3.3.
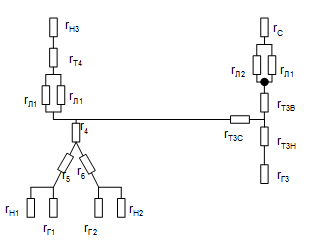
Рис. 1.1.3
Продолжаем выполнять сворачивание схемы путем объединения параллельных и последовательных сопротивлений:
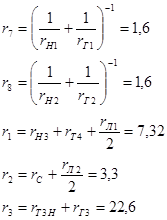
Схема приобретает вид, показанные на рис.1.3.4:
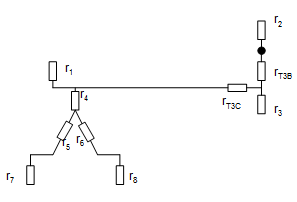
Рис. 1.1.4
После этого «сворачиваются» сопротивления 1,4,5,6,7,8:
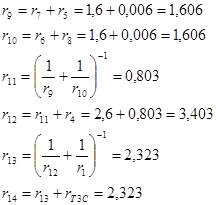
Схема приобретает вид, показанный на рис 1.3.5:
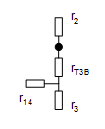
Рис. 1.1.5
Окончательно приводим схему к двух лучевому виду:
Реклама

 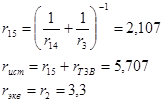
Определяем постоянные времени затухания апериодических составляющих тока КЗ:
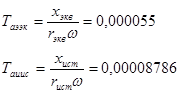
Рассчитываем значение апериодической составляющей тока в точке КЗ для момента времени t=0,1 с
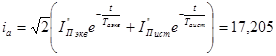 кА кА
Схема замещения прямой последовательности.
Схема замещения прямой последовательности, включая схемы замещения генераторных и нагрузочных узлов, та же, что и при симметричном трехфазном коротком замыкании.
На рис 2.1.1 представлена развернутая схема замещения прямой последовательности.
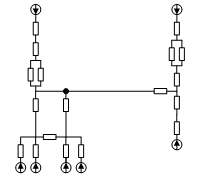
Рис. 2.1.1
Проведя ее преобразование к простейшему виду (рис.2.1.2) получим:
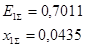
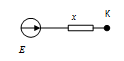
Рис. 2.1.2
Схема замещения обратной последовательности
Пути протекания токов обратной последовательности аналогичны путям протекания прямой последовательности, поэтому структурно схема замещения обратной последовательности. Исключение составляют генераторные и нагрузочные узлы, сопротивления которых считаются постоянными по величине. ЭДС. Началом обоих схем замещения считается точка нулевого потенциала, где объединены свободные концы генераторных и нагрузочных ветвей. Конец схемы – точка не симметрии, причем при продольной не симметрии имеется две точки конца. Поскольку в точке не симметрии в переходном режиме имеется остаточное напряжение, которое можно разложить на симметричные составляющие, то в точках конца подключаются напряжения U1
или U2
для поперечной не симметрии и 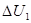 или или 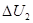 для продольной. для продольной.
Для обратной последовательности предположим, что 
Схема замещения нулевой последовательности
В силу особенности протекания токов нулевой последовательности схема замещения нулевой последовательности существенно отличается от схемы замещения прямой последовательности. Различие, в первую очередь определяется схемами замещения линий электропередач и трансформаторов. Параметры всех элементов считаются постоянными, ЭДС нулевой последовательности принимается равной нулю.
Принимаем:
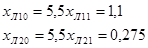
После проведения расчетов, получим:
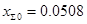
С помощью таблицы 6.2 [1, c.48] определяем дополнительное сопротивление и значение коэффициента:
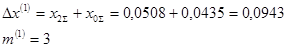
Рассчитываем ток прямой последовательности особой фазы
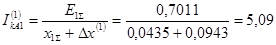
Определяем ток поврежденной фазы:
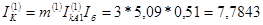 кА кА
Рассчитываем ток обратной последовательности:
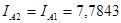 кА кА
Рассчитываем ток нулевой последовательности:
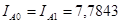 кА кА
Находим напряжение прямой последовательности:
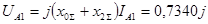 В В
Находим напряжение обратной последовательности:
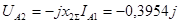 В В
Находим напряжение нулевой последовательности:
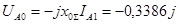
Строим векторные диаграммы токов и напряжений [2,с.215], которые показаны на рис. 2.1.3 и 2.1.4.
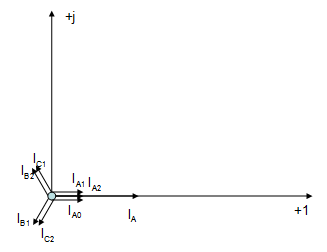
Рис. 2.1.3 Векторная диаграмма токов
Реклама

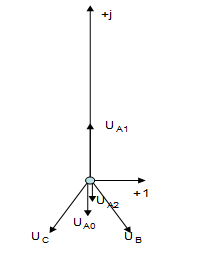
Рис. 2.1.4 Векторная диаграмма напряжений
2.2 Определить действующее значение периодической составляющей тока КЗ в указанном сечении F-F и напряжения в указанной точке М для момента времени t=0,2 с и построить соответствующие векторные диаграммы.
Расчет проводим методом спрямленных характеристик.
Поскольку t=0,2c<0,5c, то считаем, что все генераторы работают в режиме подьема возбуждения и вводим в схему замещения ЭДС 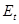 и сопротивлением и сопротивлением 
Эти параметры определяем по испрямленным характеристикам [1, c.56, рис.6.5].
Результаты заносим в таблицу 2.2.1
Таблица 2.2.1
Параметры генераторов
| Элемент
|
ЭДС
|
Сопротивление
|
Приведенное сопротивление
|
| Генератор Г-1
|
1,12
|
1,42
|
1,893
|
| Генератор Г-2
|
1,12
|
1,42
|
1,893
|
| Генератор Г-3
|
1,24
|
0,35
|
0,2979
|
| Нагрузка Н-1
|
0
|
0,35
|
0,7
|
| Нагрузка Н-2
|
0
|
0,35
|
0,7
|
| Нагрузка Н-3
|
0
|
0,35
|
1
|
Развернутая схема замещения представлена на рис. 2.2.1
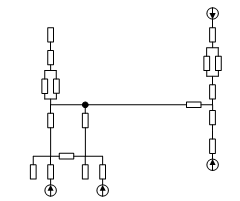
Рис.2.2.1 Схема замещения для определения
Сворачиваем схему замещения к простейшему виду и определяем эквивалентную ЭДС и результирующее сопротивление прямой последовательности аналогично пункту 2.2.1.
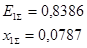
Далее принимаем сопротивление обратной последовательности равным сопротивлению прямой последовательности и повторяем расчет для нулевой последовательности.
В итоге получаем:
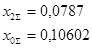
Определяем ток прямой последовательности в точке КЗ:
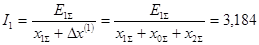
Далее находим критическое сопротивление и критический ток для каждого генератора в данный момент времени. Результаты расчетов сводим в таблицу 2.2.2
Таблица 2.2.2
Критические параметры генераторов
| Генератор
|
Критическое сопротивление
|
Критический ток
|
| Г1
|
11,8333
|
0,0845
|
| Г2
|
11,8333
|
0,0845
|
| Г3
|
1,4583
|
0,6857
|
Далее находим распределение тока прямой последовательности по ветвям схемы и определяем ток от каждого генератора.
| Генератор
|
Ток
|
| Г1
|
0,074225
|
| Г2
|
0,074225
|
| Г3
|
0,200006
|
Поскольку полученные значения токов меньше критических значений, необходимо делать перерасчет для режима нормального напряжения.
После перерасчета получим:
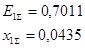
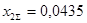
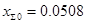
Рассчитываем ток прямой последовательности особой фазы
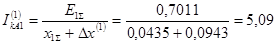
Определяем ток поврежденной фазы:
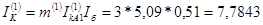 кА кА
Рассчитываем ток обратной последовательности:
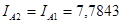 кА кА
Рассчитываем ток нулевой последовательности:
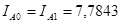 кА кА
Ток поврежденной фазы А в точке КЗ:
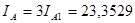 кА кА
Действующее напряжение в точке М будет равно:
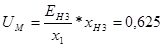
Действующее значение периодической составляющей тока КЗ в сечении F-F будет равно:
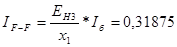 кА кА
Строим векторные диаграммы для токов и напряжений [2, c.246]
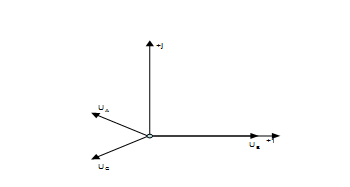
Рис.2.2.2

Рис. 2.2.3
1. «Методические указания к выполнению курсовой работы «Расчет токов короткого замыкания»», Г.К. Воронковский и др., Харьков, НТУ «ХПИ», 2004 г, 68 с.
2. «Переходные процессы в системах электроснабжения», учебник для втузов, Г.Г. Ивняк и др.,Днепропетровск, Национальный горный университет, 2003 г, 548с., ил.
|