 |
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная связь.
Чаще всего рассматриваются простейшие ситуации, когда в ходе исследования измеряют значения только одного варьирующего признака генеральной совокупности. Остальные признаки либо считаются постоянными для данной совокупности, либо относятся к случайным факторам, определяющим варьирование исследуемого признака. Как правило, исследования в спорте значительно сложнее и носят комплексный характер. Например, при контроле за ходом тренировочного процесса измеряется спортивный результат, и одновременно может оцениваться целый ряд биомеханических, физиологических, биохимических и других параметров (скорость и ускорения общего центра масс и отдельных звеньев тела, углы в суставах, сила мышц, показатели систем дыхания и кровообращения, объем физической нагрузки и энергозатраты организма на ее выполнение и т. д.). При этом часто возникает вопрос о взаимосвязи отдельных признаков. Например, как зависит спортивный результат от некоторых элементов техники спортивных движений? как связаны энергозатраты организма с объемом физической нагрузки определенного вида? насколько точно по результатам выполнения некоторых стандартных упражнений можно судить о потенциальных возможностях человека в конкретном виде спортивной деятельности? и т. п. Во всех этих случаях внимание исследователя привлекает зависимость между различными величинами, описывающими интересующие его признаки.
Этой цели служит математическое понятие функции, имеющее в виду случаи, когда определенному значению одной (независимой) переменной Х, называемой аргументом
, соответствует определенное значение другой (зависимой) переменной Y, называемой функцией
. Однозначная зависимость между переменными величинами Y
и X
называется функциональной
, т.е. Y = f(X)
(“игрек есть функция от икс”).
Например, в функции Y = 2X
каждому значению X
соответствует в два раза большее значение Y
. В функции Y = 2X2
каждому значению Y
соответствует 2 определенных значения X
. Графически это выглядит так (рис.1.1, 1.2 соответственно):
Реклама

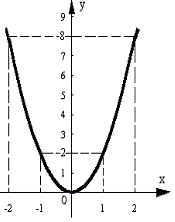 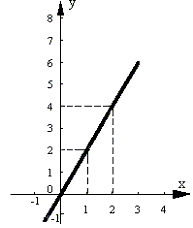
Рис.1.1. Рис.1.2.
Но такого рода однозначные или функциональные связи между переменными величинами встречаются не всегда. Известно, например, что между ростом (длиной тела) и массой человека существует положительная связь: более высокие индивиды имеют обычно и большую массу, чем индивиды низкого роста. То же наблюдается и в отношении качественных признаков: блондины, как правило, имеют голубые, а брюнеты — карие глаза. Однако из этого правила имеются исключения, когда сравнительно низкорослые индивиды оказываются тяжелее высокорослых, и среди населения хотя и нечасто, но встречаются кареглазые блондины и голубоглазые брюнеты. Причина таких “исключений” в том, что каждый биологический признак, выражаясь математическим языком, является функцией многих переменных; на его величине сказывается влияние и генетических и средовых факторов, в том числе и случайных, что вызывает варьирование признаков. Отсюда зависимость между ними приобретает не функциональный, а статистический характер
, когда определенному значению одного признака, рассматриваемого в качестве независимой переменной, соответствует не одно и то же числовое значение, а целая гамма распределяемых в вариационный ряд числовых значений другого признака, рассматриваемого в качестве независимой переменной. Такого рода зависимость между переменными величинами называется корреляционной
или корреляцией
(термин “корреляция” происходит от лат. correlatio — соотношение, связь). При этом данный вид взаимосвязи между признаками проявляется в том, что при изменении одной из величин изменяется среднее значение другой.
Если функциональные связи одинаково легко обнаружить и на единичных, и на групповых объектах, то этого нельзя сказать о связях корреляционных, которые изучаются только на групповых объектах методами математической статистики.
Задача корреляционного анализа сводится к установлению направления и формы связи между признаками, измерению ее тесноты и к оценке достоверности выборочных показателей корреляции.
Корреляционная связь между признаками может быть линейной и криволинейной (нелинейной), положительной и отрицательной.
Прямая корреляция
отражает однотипность в изменении признаков: с увеличением значений первого признака увеличиваются значения и другого, или с уменьшением первого уменьшается второй.
Обратная корреляция
указывает на увеличение первого признака при уменьшении второго или уменьшение первого признака при увеличении второго.
Например, больший прыжок и большее количество тренировок — прямая корреляция, уменьшение времени, затраченного на преодоление дистанции, и большее количество тренировок — обратная корреляция.
Реклама

1.2. Корреляционные поля и цель их построения
Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения (xi
, yi
) двух признаков. Если экспериментальных данных немного, то двумерное эмпирическое распределение представляется в виде двойного ряда значений xi
и yi
. При этом корреляционную зависимость между признаками можно описывать разными способами. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.
Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения xi
и yi
.
Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т.д.), то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами xi
и yi
г
рафически в виде геометрического места точек в системе прямоугольных координат. Эту графическую зависимость называются также диаграммой рассеивания
или корреляционным полем
.
Данная модель двумерного нормального распределения (корреляционное поле) позволяет дать наглядную графическую интерпретацию коэффициента корреляции, т.к. распределение в совокупности зависит от пяти параметров: m
x
, m
y
– средние значения (математические ожидания); s
x
,
s
y
– стандартные отклонения случайных величин Х
и Y
и р
– коэффициент корреляции, который является мерой связи между случайными величинами Х
и Y
.
Если р = 0, то значения, xi
, yi
, полученные из двумерной нормальной совокупности, располагаются на графике в координатах х, у
в пределах области, ограниченной окружностью (рис.1.3, а). В этом случае между случайными величинами Х
и Y
отсутствует корреляция и они называются некоррелированными. Для двумерного нормального распределения некоррелированность означает одновременно и независимость случайных величин Х
и Y
.
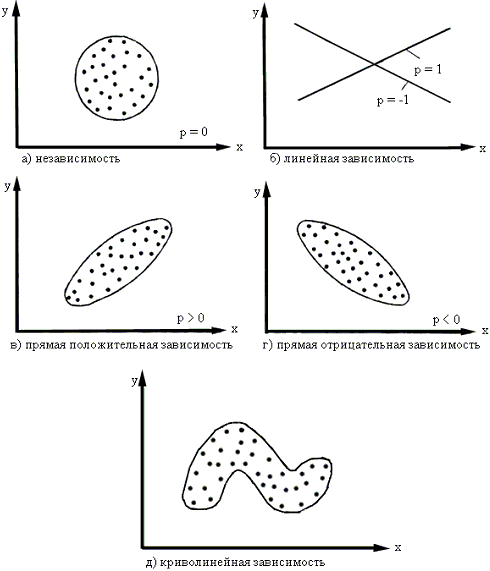
Рис.1.3. Графическая интерпретация взаимосвязи между показателями.
Если р = 1 или р = -1, то между случайными величинами Х
и Y
существует линейная функциональная зависимость (Y = c + dX)
. В этом случае говорят о полной корреляции. При р = 1 значения xi
, yi
определяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличением xi
значения yi
также увеличиваются), при р = -1 прямая имеет отрицательный наклон (рис.1.3, б).
В промежуточных случаях (-1 < p < 1)
точки, соответствующие значениям xi,
yi
,
попадают в область, ограниченную некоторым эллипсом (рис.1.3, в. г), причем при p > 0
имеет место положительная корреляция (с увеличением xi
значения yi
имеют тенденцию к возрастанию), при p < 0
корреляция отрицательная. Чем ближе р к 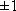 , тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии. , тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии.
Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую другую форму: парабола, гипербола и т. д. В этих случаях мы рассматривали бы так называемую, нелинейную (или криволинейную) корреляцию (рис.1.3, д).
Таким образом, визуальный анализ корреляционного поля помогает выявить не только наличия статистической зависимости (линейную или нелинейную) между исследуемыми признаками, но и ее тесноту и форму. Это имеет существенное значение для следующего шага в анализе ѕ выбора и вычисления соответствующего коэффициента корреляции.
Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида Y = f(X)
, где признак Y
– зависимая переменная
, или функция
от независимой переменной X
, называемой аргументом
. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.
Просмотрите примеры решения задач.
Пример 1.2. Определить форму и направление взаимосвязи между показателями пульса покоя и абсолютными значениями пробы PWC170
у 13 исследуемых с помощью построения графика корреляционного поля, если данные выборок таковы:
xi
, уд/мин ~ 80; 72; 71; 80; 84; 82; 78; 70; 83; 72; 72; 73; 81
yi
, кГм/мин ~ 858; 979; 1071; 920; 982; 1000; 1004; 1022; 807; 1099; 817; 879; 982
Решение
1. Построим график данного корреляционного поля, отложив на оси Х в порядке возрастания показатели пульса покоя, на оси Y — абсолютные значения пробы PWC170
.
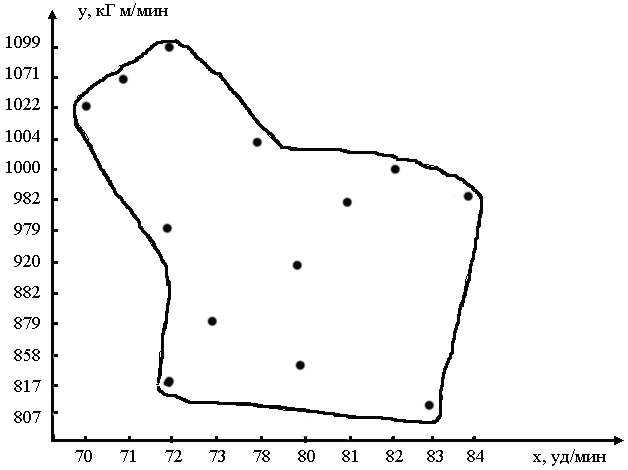
2. Сделать вывод о форме и направлении взаимосвязи между исследуемыми показателями.
Вывод: график данного корреляционного поля позволяет предположить, что, возможно, между пульса покоя и абсолютными значениями пробы PWC170
у исследуемой группы наблюдается прямая, обратная зависимость, т.е. со снижением показателя пульса покоя происходит увеличение абсолютных значений PWC170
.
Самостоятельно решите следующие задачи:
Задача 1 . Определить форму и направление взаимосвязи между результатами в беге на первой и второй половине дистанции 400 м у 13 исследуемых с помощью построения графика корреляционного поля, если данные выборок таковы:
xi
, с ~ 25,2; 26,4; 26,0; 25,8; 24,9; 25,7; 25,7; 25,7; 26,1; 25,8; 25,9; 26,2; 25,6 (первые 200 м).
yi
, с ~ 30,8; 29,4; 30,2; 30,5; 31,4; 30,3; 30,4; 30,5; 29,9; 30,4; 30,3; 30,5; 30,6 (последние 200 м).
Задача 2 . Определить форму и направление взаимосвязи между результатами в толчке штанги и прыжка в высоту с места у 12 тяжелоатлетов весовой категории до 60 кг с помощью построения графика корре-ляционного поля, если данные выборок таковы:
Результат в толчке: xi
, кг ~ 107,5; 110; 110; 115; 115; 107,5; 107,5; 120; 122,5; 112,5; 120; 110.
Прыжок в высоту с места: yi
, см ~ 57; 60; 58; 61; 63; 58; 55; 64; 65; 64; 66; 61.
Задача 3 . Определить форму и направление взаимосвязи между результатами кистевой динамометрии правой и левой рук у 7 школьников с помощью построения графика корреляционного поля, если данные выборок таковы:
Правая рука: xi
, кГ ~ 14,0; 14,2; 14,9; 15,4; 16,0; 17,2; 18,1.
Левая рука: yi
, кГ ~ 12,1; 13,8; 14,2; 13,0; 14,6; 15,9; 17,4.
1.3. Коэффициенты корреляции и их свойства.
Коэффициент корреляции р
для генеральной совокупности, как правило, неизвестен, поэтому он оценивается по экспериментальным данным, представляющим собой выборку объема n
пар значений (xi
, yi
), полученную при совместном измерении двух признаков Х
и Y
. Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции
(или просто коэффициентом корреляции
). Его принято обозначать символом r
.
Коэффициенты корреляции — удобный показатель связи, получивший широкое применение в практике. К их основным свойствам необходимо отнести следующие:
1. Коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи.
2. Значения коэффициентов корреляции – это отвлеченные числа, лежащее в пределах от —1 до +1, т.е. -1 < r < 1
.
3. При независимом варьировании признаков, когда связь между ними отсутствует, г = 0
.
4. При положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный (+)
знак и находится в пределах от 0 до +1, т.е. 0 < r 1
.
5. При отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным (–)
знаком и находится в пределах от 0 до –1, т.е. -1 < r <0
.
6. Чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к ô1ô. Если r = 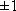 , то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х
будет соответствовать одно или несколько строго определенных значений признака Y
. , то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х
будет соответствовать одно или несколько строго определенных значений признака Y
.
7. Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы k = n –2
, где: n
– число коррелируемых пар показателей Х
и Y
. Чем больше n
, тем выше достоверность связи при одном и том же значении коэффициента корреляции.
В практической деятельности, когда число коррелируемых пар признаков Х
и Y
не велико ( 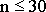 ), то при оценке зависимости между показателями используется следующую градацию: ), то при оценке зависимости между показателями используется следующую градацию:
1) высокая степень взаимосвязи
– значения коэффициента корреляции находится в пределах от 0,7 до 0,99;
2) средняя степень взаимосвязи
– значения коэффициента корреляции находится в пределах от 0,5 до 0,69;
3) слабая степень взаимосвязи
– значения коэффициента корреляции находится от 0,2 до 0,49.
1.4. Нормированный коэффициент корреляции Браве-Пирсона
В качестве оценки генерального коэффициента корреляции р используется коэффициент корреляции r
Браве–Пирсона. Для его определения принимается предположение о двумерном нормальном распределении генеральной совокупности, из которой получены экспериментальные данные. Это предположение может быть проверено с помощью соответствующих критериев значимости. Следует отметить, что если по отдельности одномерные эмпирические распределения значений xi
и yi
согласуются с нормальным распределением, то из этого еще не следует, что двумерное распределение будет нормальным. Для такого заключения необходимо еще проверить предположение о линейности связи между случайными величинами Х
и Y
. Строго говоря, для вычисления коэффициента корреляции достаточно только принять предположение о линейности связи между случайными величинами, и вычисленный коэффициент корреляции будет мерой этой линейной связи.
Коэффициент корреляции Браве–Пирсона ( 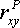 ) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле: ) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле:
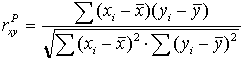 (1.1) (1.1)
Из формулы (1.1) видно, что для вычисления 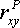 необходимо найти средние значения признаков Х
и Y
, а также отклонения каждого статистического данного от его среднего необходимо найти средние значения признаков Х
и Y
, а также отклонения каждого статистического данного от его среднего 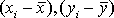 . Зная эти значения, находятся суммы . Зная эти значения, находятся суммы 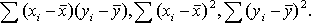 . Затем, вычислив значение . Затем, вычислив значение 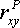 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для k = n –2
(табл. 10 приложения). Если , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для k = n –2
(табл. 10 приложения). Если 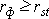 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 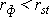 , то между признаками наблюдается недостоверная корреляционная взаимосвязь. , то между признаками наблюдается недостоверная корреляционная взаимосвязь.
Пример 1.4. Определить достоверность взаимосвязи между показателями веса и количеством подтягиваний на перекладине у 11 исследуемых с помощью расчета нормированного коэффициента корреляции, если данные выборок таковы:
xi
, кг ~ 51; 50; 48; 51; 46; 47; 49; 60; 51; 52; 56.
yi
, кол-раз ~ 13; 15; 13; 16; 12; 14; 12; 10; 18; 10; 12.
Решение
1. Расчет нормированного коэффициента корреляции Пирсона произвести по формуле (1):
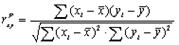 (1) (1)
| xi
|
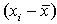 |
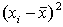 |
yi
|
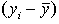 |
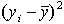 |
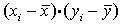 |
| 51 |
0 |
0 |
13 |
0 |
0 |
0 |
| 50 |
-1 |
1 |
15 |
2 |
4 |
-2 |
| 48 |
-3 |
9 |
13 |
0 |
0 |
0 |
| 51 |
0 |
0 |
16 |
3 |
9 |
0 |
| 46 |
-5 |
25 |
12 |
-1 |
1 |
5 |
| 47 |
-4 |
16 |
14 |
1 |
1 |
-4 |
| 49 |
-2 |
4 |
12 |
-1 |
1 |
2 |
| 60 |
9 |
81 |
10 |
-3 |
9 |
-27 |
| 51 |
0 |
0 |
18 |
5 |
25 |
0 |
| 52 |
1 |
1 |
10 |
-3 |
9 |
-3 |
| 56 |
5 |
25 |
12 |
-1 |
1 |
-5 |
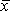 =
51 =
51 |
 |
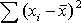 = 162 = 162
|
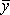 = 13 = 13
|
 |
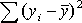 = 60 = 60
|
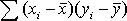 = - 34 = - 34
|
Тогда
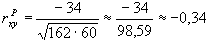
3. Рассчитать число степеней свободы по формуле (2):
К = n –2
(2)
K = 11 – 2 = 9
4. Сравнить расчетное значение нормированного коэффициента корреляции (rф
= -0,34) с табличным значением для К = 9
при a = 5% (табл.1 приложения) и сделать вывод.
Вывод:
1) т.к. rф
= -0,34 < 0, то между данными выборок наблюдается прямая отрицательная взаимосвязь, т.е. с увеличение показателей веса у исследуемых снижается их результат в количестве подтягиваний на перекладине;
2) т.к. rф
= -0,34 < rst
= 0,60 для K = 10 при a = 5%, то с уверенностью b = 95% можно говорить о том, что выявленная зависимость недостоверна.
Задания на тему лекции
Самостоятельно решите следующие задачи:
Задача 1.
Определить достоверность взаимосвязи между показателями веса и результатами прыжков в длину с места у 9 исследуемых с помощью расчета нормированного коэффициента корреляции, если данные выборок таковы:
Показатели веса: xi
, кг ~ 66; 80; 73; 74; 85; 79; 68; 71; 70.
Результаты прыжков: yi
, см ~ 203; 185; 199; 197; 183; 205; 217; 190; 200.
Задача 2.
Определить достоверность взаимосвязи между показателями пульса покоя и пульса восстановления 8 исследуемых с помощью рас-чета нормированного коэффициента корреляции, если данные выборок таковы:
ЧСС покоя: xi
, уд/мин ~ 66; 80; 73; 74; 85; 79; 68; 71.
ЧСС восстановления: yi
, уд/мин ~ 70; 85; 78; 78; 90; 84; 66; 72.
Задача 3.
Определить достоверность взаимосвязи между результатами времени прохождения дистанции и показателями абсолютных значений в пробе PWC170
у 10 юных яхтсменов с помощью расчета нормированного коэффициента корреляции, если данные выборок таковы:
Результат на дистанции:
xi
, с ~ 61,3; 65,0; 79,3; 80,0; 74,7; 72,0; 72,0; 61,7; 79,3; 74,7; 65,7.
Проба PWC170
:
yi
, кГм/мин ~ 917; 875; 810; 608; 746; 632; 710; 850; 911;. 732; 915.
1.5. Коэффициент ранговой корреляции Спирмена
Если потребуется установить связь между двумя признаками, значения которых в генеральной совокупности распределены не по нормальному закону, т. е. предположение о том, что двумерная выборка (xi
и yi
) получена из двумерной нормальной генеральной совокупности, не принимается, то можно воспользоваться коэффициентом ранговой корреляции Спирмена (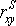 ): ):
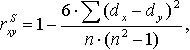 (1.2) (1.2)
где: dx
и dy
– ранги показателей xi
и yi
;
n
– число коррелируемых пар.
Коэффициент ранговой корреляции также имеет пределы 1 и –1. Если ранги одинаковы для всех значений xi
и yi
, то все разности рангов (dx
- dy
) = 0
и = 1. Если ранги xi
и yi
расположены в обратном порядке, то 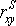 = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi
и yi
. = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi
и yi
.
Когда ранги всех значений xi
и yi
строго совпадают или расположены в обратном порядке, между случайными величинами Х
и Y
существует функциональная зависимость, причем эта зависимость не обязательно линейная, как в случае с коэффициентом линейной корреляции Браве-Пирсона, а может быть любой монотонной зависимостью (т. е. постоянно возрастающей или постоянно убывающей зависимостью). Если зависимость монотонно возрастающая, то ранги значений xi
и yi
совпадают и 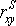 = 1; если зависимость монотонно убывающая, то ранги обратны и = 1; если зависимость монотонно убывающая, то ранги обратны и 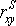 = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х
и Y
. = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х
и Y
.
Из формулы (8.2) видно, что для вычисления 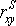 необходимо сначала проставить ранги (dx
и dy
) показателей xi
и yi
, найти разности рангов (dx
- dy
)
для каждой пары показателей и квадраты этих разностей (dx
- dy
)2
. Зная эти значения, находятся суммы необходимо сначала проставить ранги (dx
и dy
) показателей xi
и yi
, найти разности рангов (dx
- dy
)
для каждой пары показателей и квадраты этих разностей (dx
- dy
)2
. Зная эти значения, находятся суммы 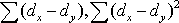 , учитывая, что , учитывая, что 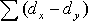 всегда равна нулю. Затем, вычислив значение всегда равна нулю. Затем, вычислив значение 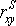 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным (табл. 9 приложения). Если , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным (табл. 9 приложения). Если 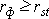 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 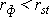 , то между признаками наблюдается недостоверная корреляционная взаимосвязь. , то между признаками наблюдается недостоверная корреляционная взаимосвязь.
Коэффициент ранговой корреляции Спирмена вычисляется значительно проще, чем коэффициент корреляции Браве-Пирсона при одних и тех же исходных данных, поскольку при вычислении используются ранги, представляющие собой обычно целые числа.
Коэффициент ранговой корреляции целесообразно использовать в следующих случаях:
1. Если экспериментальные данные представляют собой точно измеренные значения признаков Х
и Y
и требуется быстро найти приближенную оценку коэффициента корреляции. Тогда даже в случае двумерного нормального распределения генеральной совокупности можно воспользоваться коэффициентом ранговой корреляции вместо точного коэффициента корреляции Браве-Пирсона. Вычисления будут существенно проще, а точность оценки генерального параметра р
с помощью коэффициента 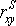 при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций. при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций.
2. Когда значения xi
и (или) yi
заданы в порядковой шкале (например, оценки судей в баллах, места на соревнованиях, количественные градации качественных признаков), т. е. когда признаки не могут быть точно измерены, но их наблюдаемые значения могут быть расставлены в определенном порядке.
Пример 1.6. Определить достоверность взаимосвязи между показателями веса и максимального количества сгибания и разгибания рук в упоре лежа у 10 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
xi
, кг ~ 55; 45; 43; 47; 47; 51; 48; 60; 53; 50
yi
, кол-во раз ~ 26; 20; 25; 22; 27; 28; 16; 15; 18; 24
Решение
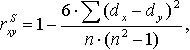 (1) (1)
где: dx
и dy
— ранги показателей х
и у
;
n
— число коррелируемых пар или исследуемых.
2. Данные тестирования занести в рабочую таблицу и сделать необходимые расчеты.
| xi
|
dx
|
yi
|
dy
|
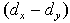 |
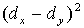 |
| 55 |
9 |
26 |
9 |
0 |
0 |
| 45 |
2 |
20 |
4 |
-2 |
4 |
| 43 |
1 |
25 |
7 |
-6 |
36 |
| 47 |
3.5 |
22 |
5 |
-1.5 |
2.25 |
| 47 |
3.5 |
7 |
8 |
-4.5 |
20.25 |
| 51 |
7 |
28 |
10 |
-3 |
9 |
| 48 |
5 |
16 |
2 |
3 |
9 |
| 60 |
10 |
15 |
1 |
9 |
81 |
| 53 |
8 |
18 |
3 |
5 |
25 |
| 50 |
6 |
24 |
6 |
0 |
0 |
 |
 |
 |
 |
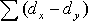 = 0 = 0
|
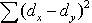 = 186,5 = 186,5 |
Тогда
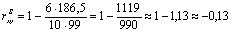
3. Сравнить расчетное значение рангового коэффициента корреляции (rф
= -0,13) с табличным значением для n = 10 при a = 5% (табл.2 приложения) и сделать вывод.
Вывод:
1) т.к. rф
= -0,13 < 0, то между данными выборок наблюдается прямая отрицательная взаимосвязь, т.е. увеличением показателей веса вызывает снижение максимального количество сгибаний и разгибаний рук в упоре лежа в группе исследуемых;
2) т.к. rф
= -0,13 < rst
= 0,64 для n = 10 при a = 5%, то с уверенностью b = 95% можно говорить о том, что выявленная зависимость недостоверна.
Задания по теме лекции
Самостоятельно решите следующие задачи:
Задача 1.
Определить достоверность взаимосвязи между показателями длины прыжков с места и с разбега 10 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
Прыжок с места: xi
, см ~ 216; 180; 230; 224; 185; 209; 218; 250; 249; 254.
Прыжок с разбега: yi
, см ~ 313; 275; 330; 320; 300; 315; 315; 370; 365; 330.
Задача 2.
Определить достоверность взаимосвязи между показателями становой динамометрии и количеством подтягиваний на перекладине у 9 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
Становая динамометрия: xi
, кГ ~ 156; 130; 143; 124; 135; 125; 138; 141; 139.
Подтягивание на перекладине: yi
, кол-во раз ~ 16; 15; 20; 20; 16; 15; 15; 20; 15.
Задача 3.
Определить достоверность взаимосвязи между показателями индекса Кетле и местами в соревнованиях у 11 акробатов с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
Индекс Кетле: xi
, г/см ~ 389; 370; 382; 358; 358; 366; 370; 354; 382; 363; 350.
Место: yi
,
~ 5; 2; 6; 10; 11; 1; 3; 9; 4; 7; 8.
|