Федеральное Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу "Общая физика"
ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
НА МАШИНЕ АТВУДА
Преподаватель Студент группы
___________ / / / /
___________2010 г. 2010 г.
2010 г.
1. ЦЕЛЬ РАБОТЫ
Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное - по риске на корпусе среднего кронштейна.
Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.
Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средние значения времени <t
> и квадрата времени < t
2
> прохождения грузом с перегрузкомпути S:
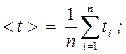
(3.1)
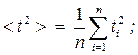
(3.2)
Случайная погрешность измерения времени прохождения пути S:
σсл
(t
) = t(a, n
) ×S
(t
) ; (3.3)
где t(a, n
) - коэффициент Стьюдента
Стандартная погрешность измерения времени:
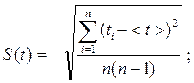
(3.4)
где
ti
- времени прохождения пути при i
–ом
измерении ( i
=1. … , n
),
n
– число измерений, < t
> - среднее значение времени прохождения пути.
Реклама

Общая погрешность:
 (3.5) (3.5)
где: 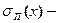 приборная погрешность. приборная погрешность.
Угловой коэффициент экспериментальной прямой:
b =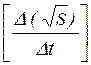 (3.6)
(3.6)
Величина ускорения, определяемого из линеаризованного графика:
a
= 2b2
(3.7)
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Измеренные значения и результаты их обработки приведены в таблице 4.1.
Результаты прямых и косвенных измерений Таблица 4.1
| S
1
= 0,401 м |
S
2
= 0,351 м |
S
3
= 0,3 м |
S
4
= 0,251 м |
S
5
= 0,201 м |
| Номер измерения |
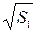 =0,633 м1/2 =0,633 м1/2
|
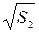 = 0,592 м1/2 = 0,592 м1/2
|
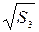 = 0,547 м1/2 = 0,547 м1/2
|
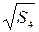 = 0,5 м1/2 = 0,5 м1/2
|
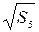 =0,448 м1/2 =0,448 м1/2
|
| t
, c |
t
2
, c2
|
t
, c |
t
2
, c2
|
t
, c |
t
2
, c2
|
t
, c |
t
2
, c2
|
t
, c |
t
2
, c2
|
| 1 |
4,377 |
8,754 |
3,952 |
7,904 |
3,952 |
7,904 |
3,378 |
6,756 |
3,054 |
6,108 |
| 2 |
4,608 |
9,216 |
4,053 |
8,106 |
3,952 |
7,904 |
3,434 |
6,868 |
3,285 |
6,57 |
| 3 |
4,536 |
9,072 |
3,973 |
7,946 |
3,861 |
7,722 |
3,641 |
7,282 |
3,003 |
6,006 |
| 4 |
4,589 |
9,178 |
4,206 |
8,412 |
3,663 |
7,326 |
3,469 |
6,938 |
3,220 |
6,44 |
| 5 |
4,235 |
8,47 |
4,317 |
8,634 |
3,913 |
7,826 |
3,497 |
6,994 |
3,292 |
6,584 |
| < t
>, c |
4,469 |
4,100 |
3,868 |
3,483 |
3,171 |
| < t
2
>, c2
|
19,972 |
16,81 |
14,961 |
12,131 |
10,055 |
Средние значения времени <t
> и квадрата времени < t
2
> прохождения пути S, приведенные в таблице 4.1, рассчитаны по выражениям 3.1 и 3.2 (число точек измерения n=5 ).
Для определения случайной погрешности измерения, предварительно определим стандартную погрешность измерения, по формуле (3.4)
Для первой точки измерения (S
1
= 40,1 см):
Δt1
= t1
−< t>1
= 4,377-4,469= -0,092 с; Δt1
2
= (-0,092)2
= 0,008464с2
,
Δt2
= t2
−< t>1
= 4,608 -4,469= 0,139 с; Δt2
2
= (0,139)2
= 0,019321с2
,
Δt3
= t3
−< t>1
= 4,536-4,469= 0,067 с; Δt3
2
= (0,067)2
= 0,004489с2
,
Δt4
= t4
−< t>1
= 4,589-4,469= 0,12 с; Δt4
2
= (0,12)2
= 0,0144 с2
,
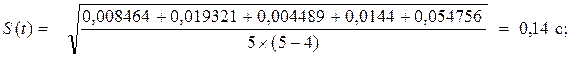 Δt5
= t5
−< t>1
= 4,235 -4,469= -0,234 с; Δt5
2
= (-0,234)2
= 0,054756 с2
, Δt5
= t5
−< t>1
= 4,235 -4,469= -0,234 с; Δt5
2
= (-0,234)2
= 0,054756 с2
,
Для второй точки измерения (S
2
= 35,1 см):
Δt1
= t1
−< t>1
= 3,952-4,100= -0,148 с; Δt1
2
= (-0,148)2
= 0,0219с2
,
Δt2
= t2
−< t>1
= 4,053 -4,100= -0,047 с; Δt1
2
= (-0,047)2
= 0,00220с2
;
Δt3
= t3
−< t>1
= 4,973-4,100= 0,873 с; Δt1
2
= (0,873)2
= 0,762с2
;
Δt4
= t4
−< t>1
= 4,206-4,100= 0,094 с; Δt1
2
= (0,094)2
= 0,00883 с2
;
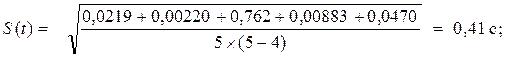 Δt5
= t5
−< t>1
= 4,317 -4,100= 0,217 с; Δt1
2
= (0,217)2
= 0,0470 с2
; Δt5
= t5
−< t>1
= 4,317 -4,100= 0,217 с; Δt1
2
= (0,217)2
= 0,0470 с2
;
Для третьей точки измерения (S
3
= 40,1 см):
Δt1
= t1
−< t>1
= 3,952-3,868= 0,084 с; Δt1
2
= (0,084)2
= 0,00705с2
,
Δt2
= t2
−< t>1
= 3,952 -3,868= 0,084 с; Δt2
2
= (0,084)2
= 0,00705с2
,
Δt3
= t3
−< t>1
= 3,861-3,868= -0,007 с; Δt3
2
= (-0,007)2
= 0,000049с2
,
Δt4
= t4
−< t>1
= 3,663-3,868= -0,205 с; Δt4
2
= (-0,205)2
= 0,0420 с2
,
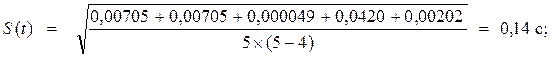 Δt5
= t5
−< t>1
= 3,913 -3,868= 0,045 с; Δt5
2
= (0,045)2
= 0,00202 с2
, Δt5
= t5
−< t>1
= 3,913 -3,868= 0,045 с; Δt5
2
= (0,045)2
= 0,00202 с2
,
Для четвертой точки измерения (S
4
= 25,1 см):
Реклама

Δt1
= t1
−< t>1
= 3,378-3,483= -0,105 с; Δt1
2
= (-0,105)2
= 0,0110с2
;
Δt2
= t2
−< t>1
= 3,434 -3,483= -0,049 с; Δt2
2
= (-0,049)2
= 0,00240с2
;
Δt3
= t3
−< t>1
= 3,641-3,483= 0,158 с; Δt3
2
= (0,158)2
= 0,0249с2
;
Δt4
= t4
−< t>1
= 3,469-3,483= -0,014 с; Δt4
2
= (-0,014)2
= 0,00019 с2
;
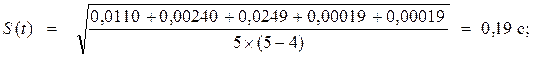 Δt5
= t5
−< t>1
= 3,497 -3,483= 0,014 с; Δt5
= t5
−< t>1
= 3,497 -3,483= 0,014 с;
Δt5
2
= (0,014)2
= 0,00019
Для пятой точки измерения (S
5
= 20,1 см):
Δt1
= t1
−< t>1
= 3,054-3,171= -0,117 с; Δt1
2
= (-0,117)2
= 0,0137с2
,
Δt2
= t2
−< t>1
= 3,285 -3,171= 0,141 с; Δt2
2
= (0,141)2
= 0,0199с2
,
Δt3
= t3
−< t>1
= 3,003-3,171= -0,168 с; Δt3
2
= (-0,168)2
= 0,0282с2
,
Δt4
= t4
−< t>1
= 3,220-3,171= 0,049 с; Δt4
2
= (0,049)2
= 0,00240 с2
,
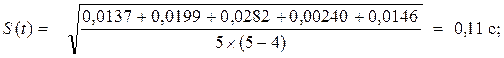 Δt5
= t5
−< t>1
= 3,292 -3,171= 0,121 с; Δt5
2
= (0,121)2
= 0,0146 с2
, Δt5
= t5
−< t>1
= 3,292 -3,171= 0,121 с; Δt5
2
= (0,121)2
= 0,0146 с2
,
Таблица 4.2 Стандартная погрешность для каждой точки измерения
| S1
|
S2
|
S3
|
S4
|
S5 |
| S(t)
|
0,14 |
0,41 |
0,14 |
0,19 |
0,11 |
S
(
t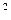 )
)
|
0,0196 |
0,1681 |
0,019 |
0,0361 |
0,121 |
Так, как доверительная вероятность α не оговорена в задании, то предположим, что доверительная вероятность α = 0,95. Тогда коэффициент Стьюдента t =
2,8.
Используя формулу (3.3) находим случайную погрешность для экспериментальных точек измерения.
Для первой точки измерения (S1).
Ơ 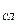 (t)= 2,8*0,14=0,392. (t)= 2,8*0,14=0,392.
Для второй точки измерения (S2).
Ơ 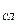 (t)= 2,8*0,41=1,148. (t)= 2,8*0,41=1,148.
Для третьей точки измерения (S3).
Ơ 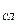 (t)= 2,8*0,14=0,392. (t)= 2,8*0,14=0,392.
Для четвертой точки измерения (S4).
Ơ 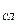 (t)= 2,8*0,19=0,532. (t)= 2,8*0,19=0,532.
Для пятой точки измерения (S5).
Ơ 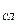 (t)= 2,8*0,11=0,308. (t)= 2,8*0,11=0,308.
Таблица 4.3
Случайная погрешность для каждой точки измерения
| S1
|
S2
|
S3
|
S4
|
S5
|
Ơ 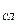 (t) (t) |
0,392 |
1,148 |
0,392 |
0,532 |
0,308 |
Ơ
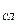 (
t
(
t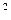 )
)
|
0,1536 |
1,3179 |
0,1536 |
0,283 |
0,0948 |
Так, как на миллисекундомере не обозначен класс точности прибора
и он является цифровым, то его погрешность составляет 1 единица
младшего разряда, т. е. 0.001 с. Тогда общая погрешность для каждой
из точек составит:
Для первой точки измерения (S1):
Δ(х)= 0,392+0,001=0,393.
Для второй точки измерения (S2):
Δ(х)= 1,148+0,001=1,149.
Для третьей точки измерения (S3):
Δ(х)= 0,392+0,001=0,393.
Для четвертой точки измерения (S4):
Δ(х)= 0,532+0,001=0,533.
Для пятой точки измерения (S5):
Δ(х)= 0,308+0,001=0,309.
Таблица4.4
Общая погрешность для каждой точки измерения
| S1
|
S2
|
S3
|
S4
|
S5 |
| (t), c |
±0,393 |
±1,149 |
±0,393 |
±0,533 |
±0,309 |
(t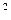 ), c ), c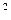 |
±0,154 |
±1,320 |
±0,154 |
±0,284 |
±0,095 |
Таблица 4.5
Доверительные интервалы для каждой точки измерения
| S1
|
S2
|
S3
|
S4
|
S5
|
| (t),с |
4,469±0,393 |
4,100±1,149 |
3,868±0,393 |
3,483±0,533 |
3,171±0,309 |
(t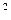 ),с ),с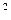 |
19,97±0,154 |
16,81±1,320 |
14,96±0,154 |
12,131±0,284 |
10,055±0,095 |
Строим графики зависимости.
   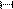    
Рисунок 4.1. Зависимость пройденного пути S
от времени t
.
S
=
f
 (
t
).
(
t
).
        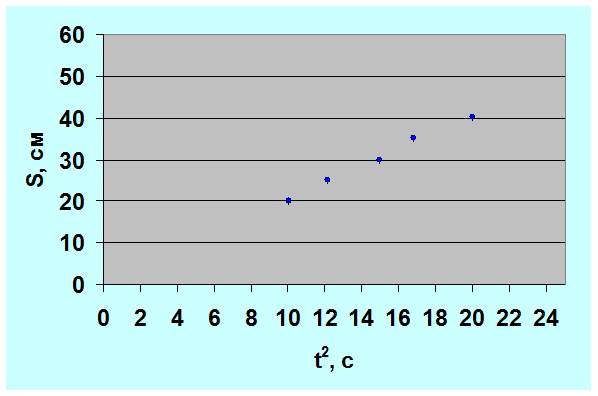 Рисунок 4.2. Зависимость пройденного пути S
от квадрата времени t
2
.
S
=
f Рисунок 4.2. Зависимость пройденного пути S
от квадрата времени t
2
.
S
=
f
 (
t (
t ).
).
 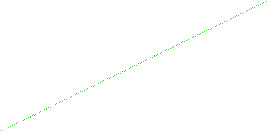           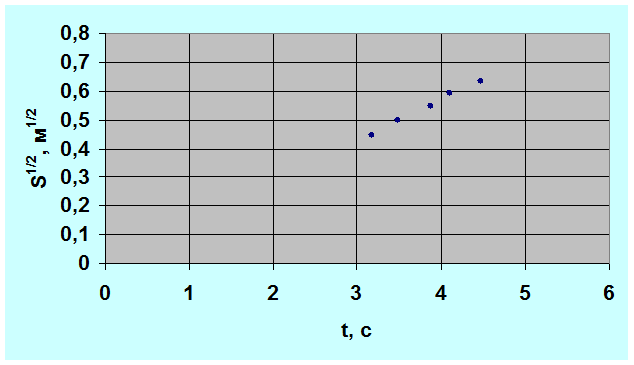 Рисунок 4.3.Зависимость Рисунок 4.3.Зависимость 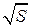 от времени t
. от времени t
.
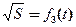 .
.
По графику 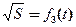 , находим значения Δ , находим значения Δ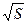 и Δt .
и Δt .
Используя формулы (3.6) и (3.7) найдем величину ускорения 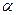 , определяемого из линеаризованного графика , определяемого из линеаризованного графика 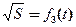 . .
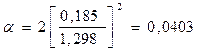 м/с м/с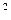
5. ВЫВОДЫ
В результате проделанной работы, с помощью машины Атвуда, мы убедились в справедливости закона прямолинейного ускоренного движения тел под действием силы земного притяжения, так как смогли в пределах погрешностей измерений, построить линеаризованный график зависимости 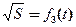 и рассчитать величину ускорения движения грузов. и рассчитать величину ускорения движения грузов.
6.КОНТРОЛЬНЫЕ ВОПРОСЫ.
6.1.Какие силы действуют на груз сперегрузком во время движения?
На груз с перегрузком действуют следующие силы:
- сила тяжести груза;
- сила тяжести перегрузка;
- сила натяжения нити.
6.2. Запишите уравнения движения для каждого из грузов.
Согласно второго закона Ньютона, уравнение движения будет иметь вид:
Для груза с перегрузком:
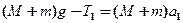 ; ;
где (M
+
m
)
g
-
масса груза с перегрузком, 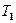 -сила натяжения нити. -сила натяжения нити.
Для второго груза:
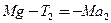 ; ;
где Mg
-
масса второго груза, T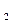 -
сила натяжения нити.
-
сила натяжения нити.
6.3. Укажите возможные причины несовпадения теоретических выводов
с результатами измерений.
В качестве возможных причин можно предположить:
- большие погрешности измерения;
- инерционность блока в машине Атвуда.
6.4. Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени?
Систематическая погрешность измерения времени может повлиять
на линеаризованный график таким образом, что прямая будет проходить
не через начало системы координат, а с некоторым смещением, это и будет
видно на линеаризованном графике.
6.5. Укажите физические допущения, используемые при теоретическом
анализе движения грузов в машине Атвуда.
При проведении данной лабораторной работы мы не учитывали
следующие параметры:
- сила трения блока;
- сила трения нити и блока;
- вес блока;
- вес нити;
- растяжением нити.
7. ПРИЛОЖЕНИЕ
К работе прилагается регистрационный файл (phyLab1.reg).
|