Міністерство освіти і науки України
Курсова робота на тему:
Порівняльний аналіз ефективності та складності алгоритмів сортування файлів і послідовностей
Зміст
Вступ
1. Сортування прямим злиттям
2. Природне злиття
3. Метод злиття впорядкованих серій
4. Багатофазне злиття
Висновки
Література
Додатки
Вступ
Комп’ютери тісно увійшли в наше життя. Ми і не помітили, як вони заполонили всі галузі нашого господарства, зайдеш в супермаркет – візьмеш товар, тобі автоматично виб’ють чек за штрих кодом, в бібліотеку зайдеш – по каталогу знайдуть потрібну книжку і скажуть в якому ряду і на якій полиці вона розміщена. Потрібно знайти реферат, - будь-ласка, заходиш в Інтернет-кафе, відкриваєш пошуковий сервер, вводиш слова із потрібної теми і вже за секунду тобі відкриваються посилання на можливі сайти. Аналогічним чином ви заходите в магазин і замовляєте вкрай необхідну деталь для вашої пральної машини і вже за секунду вам повідомляють чи є вона на прилавку магазину, чи можливо лежить неподалік на складі чи її зможуть замовити і привезти наступного тижня.
Проте рідко хто задумувався, як так швидко ви отримуєте цю інформацію? А все дуже просто, існує певна база даних, по ній проводиться пошук і вже по результатах вибірки робляться висновки. Зрозуміло, рядовому користувачу вникати в деталі неважливо, проте ми в своїй курсовій роботі зачепимо ряд питань.
Так, пошук проводиться в базі даних. Для того щоб він був швидкий, база даних повинна бути впорядкована. Отже, хоч програмування містить цілу низку важливих внутрішніх задач, та все ж однією з найбільш важливих таких задач для програмування є задача сортування. Під сортуванням звичайно розуміють перестановки елементів будь-якої послідовності у визначеному порядку. Ця задача є однією з найважливіших тому, що її метою є полегшення подальшої обробки певних даних і, насамперед, задачі пошуку. Так, одним з ефективних алгоритмів пошуку є бінарний пошук. Він працює швидше ніж, наприклад, лінійний пошук, але його можливо застосовувати лише за умови, що послідовність вже упорядкована, тобто відсортована.
Взагалі, відомо, що в будь-якій сфері діяльності, що використовує комп’ютер для запису, обробки та збереження інформації, усі дані зберігаються в базах даних, які також потребують сортування. Певна впорядкованість для них дуже важлива, адже користувачеві набагато легше працювати з даними, що мають певний порядок. Так, можна розташувати всі товари по назві або відомості про співробітників чи студентів за прізвищем або роком народження, тощо.
Реклама

Задача сортування в програмуванні не вирішена повністю. Адже, хоча й існує велика кількість алгоритмів сортування, все ж таки метою програмування є не лише розробка алгоритмів сортування елементів, але й розробка саме ефективних алгоритмів сортування. Ми знаємо, що одну й ту саму задачу можна вирішити за допомогою різних алгоритмів і кожен раз зміна алгоритму приводить до нових, більш або менш ефективних розв’язків задачі. Основними вимогами до ефективності алгоритмів сортування є перш за все ефективність за часом та економне використання пам’яті. Згідно цих вимог, прості алгоритми сортування (такі, як сортування вибором і сортування включенням) не є дуже ефективними.
З винайденням комп’ютерної техніки проблемою створення алгоритмів сортування займалося дуже багато людей. Проводилися досліди, експерименти із швидкодії одних методів і їх переваги над іншими, наводилися їх математичні моделі для оцінки затраченого часу виконання.
З часом, ці методи були розбиті на декілька категорій, найбільш відомі серед яких, це прямі методи сортування масивів і послідовностей:
- сортування прямим включенням.
- сортування бінарним включенням.
- сортування прямим вибором.
- сортування прямим обміном.
Та швидкі методи сортування:
- сортування алгоритмом Шелла;
- сортування алгоритмом Quick Sort;
- сортування алгоритмом Тree Sort;
- сортування алгоритмом Heap Sort.
Звичайно, це не всі методи сортування масивів. Та з часом виявилося, що вони не повністю вичерпують проблеми пов’язані із питанням сортування. Так, в реальних задачах виникають послідовності, що зберігаються в файлах і не можуть уміщатися в оперативній пам'яті у вигляді масивів. Наприклад, у великому місті може бути кілька мільйонів абонентів телефонної мережі. Звичайно, для швидкого пошуку дані про абонентів мають бути відсортованими. Виникає задача сортування файлів за умови, що файли цілком не можна подавати в оперативній пам'яті. Тому, алгоритми сортування стали ще умовно поділяти не лише на прямі та швидкі а і на внутрішні (ті що обробляються оперативною пам’яттю) та зовнішні.
Реклама

Метою роботи є: Знайомство з теоретичним положенням, що стосуються методів сортування файлів, реалізація їх на мові програмування Turbo Pascal.
Предмет дослідження: Зовнішні алгоритми сортування послідовностей.
Об'єкт дослідження: Математична модель доцільності використання зовнішніх алгоритмів сортування на практиці.
Досягненням мети й відповідно до поставленої гіпотези визначаються наступні завдання:
1. Вивчити літературу по темі алгоритми сортування файлів;
2. Проаналізувати зовнішні методи сортування;
3. Реалізувати на Turbo Pascal алгоритми сортування файлів довільної величини;
4. Розробити закінчений програмний продукт по темі дослідження;
5. Провести аналіз математичних моделей різних методів.
1. Сортування прямим злиттям
Перш ніж розглядати зовнішні алгоритми сортування, давайте подумаємо, яким же чином можна відсортувати величезний файл, що не поміщається в оперативній пам’яті? Перше, що приходить на розум, це взяти його, розбити на велику кількість файлів і відсортувавши кожен потім злити. Тому, давайте розглянемо приклад злиття двох відсортованих масивів та проведемо аналіз швидкості його виконання.
Злиття двох упорядкованих послідовностей можна порівняти з перебудовою двох колон солдатів, вишикуваних за зростом, в одну, де вони також розташовуються за зростом. Якщо цим процесом керує офіцер, то він порівнює зріст солдатів, перших у своїх колонах і вказує, якому з них треба ставати останнім у нову колону, а кому залишатися першим у своїй. Так він вчиняє, поки одна з колон не вичерпається – тоді решта іншої колони додається до нової.
Нехай у масиві Y з елемента Y[m] починається впорядкована ділянка довжиною s, а з елемента Y[m+s] – впорядкована ділянка довжини r. Наприклад,
| Y |
… |
1 |
3 |
… |
13 |
2 |
4 |
… |
88 |
| … |
M |
m+1 |
m+s-1 |
m+s |
m+s+1 |
… |
m+s+r |
Результатом злиття повинна бути ділянка довжини r+s у масиві X:
| X |
… |
1 |
2 |
3 |
4 |
… |
13 |
… |
88 |
| … |
m |
m+1 |
m+2 |
m+3 |
… |
m+s+r |
Дане злиття двох ділянок у масиві Y у ділянку масиву X задає процедура:
procedure mrg(var Y: ArT; m, s, r: Indx; var X: ArT);
var mr, k: Indx; i, j: Extind;
begin
mr:= m + s; { mr – початок правої частини }
i:= m; j:= mr; { i та j пробігають ліву й праву ділянки масиву Y}
for k:= m to m + s + r - 1 do {заповнення X[m], …, X[m+s+r-1]}
if i > m + s - 1 then begin X[k]:= Y[j]; j:= j + 1 end
else if j > mr + r - 1 then
begin X[k]:= Y[i]; i:= i + 1 end else
if Y[i] < Y[j] then
begin X[k]:= Y[i]; i:= i + 1 end else
begin X[k]:= Y[j]; j:= j + 1 end
end;
Тепер розглянемо сортування масиву A злиттям. На першому кроці елементи A[1], …, A[n] копіюються в допоміжний масив B[1], …, B[n]. Його елементи розглядаються парами B[1] і B[2], B[3] і B[4] тощо, як упорядковані послідовності довжиною lp = 1 і зливаються за допомогою процедури mrg в масив A. Тепер там є впорядковані ділянки довжиною 2. За непарного n останній елемент A[n] залишається без змін як послідовність довжиною 1.
На наступному кроці після копіювання в масив B зливаються пари упорядкованих ділянок B[1]B[2] і B[3]B[4], B[5]B[6] і B[7]B[8] тощо. З'являються впорядковані ділянки довжиною 4. Нехай t=n mod 4 – довжина залишку масиву після останньої повної четвірки елементів. При t=1 або t=2 останні t елементів утворюють упорядковану ділянку після попереднього кроку. При t=3 зливаються упорядкована пара B[n-1]B[n-2] та ділянка B[n] у ділянку довжиною t.
Кроки повторюються з подвоєнням довжин упорядкованих ділянок lp, поки lp < n.
Розглянемо сортування злиттям масиву <11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1> довжини n=11. Упорядковані послідовності в ньому вказуються в дужках <>, а пари таких, що зливаються, відокремлені ";":
< <11><10>; <9><8>; <7><6>; <5><4>; <3><2>; <1> >, lp=1
< <10, 11><8, 9>; <6, 7><4, 5>; <2, 3><1> >, lp=2
< <8, 9, 10, 11><4, 5, 6, 7>;<1, 2, 3> >, lp=4
< <4, 5, 6, 7, 8, 9, 10, 11><1, 2, 3> >, lp=8
<1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11>, lp=16, lp³ n.
Як бачимо, нам знадобилося 4 кроки злиття для того, щоб одержати впорядований масив.
Даний спосіб сортування можна описати наступною процедурою Mrgsort:
procedure Mrgsort (var A: ArT; n: Indx);
var B: ArT;
lp, npp, cpp, bpp, tl: integer;
begin
lp:= 1;
while lp < n do
begin
B:= A; { копіювання }
npp:= n div (2*lp); { кількість пар ділянок }
tl:= n mod (2*lp); { довжина залишку }
for cpp:= 1 to npp do { cpp – номер пари }
begin
bpp:= (cpp - 1)*2*lp + 1;
{ індекс першого елемента лівої ділянки пари}
mrg (B, bpp, lp, lp, A);
end;
{ обробка залишку }
if tl > lp then
mrg (B, n - tl + 1, lp, tl - lp, A);
{ за tl <= lp залишок був упорядкований }
{ на попередньому кроці }
lp:= lp*2
end;
{ lp >= n: масив упорядковано на останньому кроці }
end;
Очевидно, що після k-го кроку впорядковані ділянки мають довжину lp=2k
. Якщо 2k
=n, то масив упорядковано. Якщо 2k
>n, але 2k-1
<n, то при виконанні останнього кроку мають місце співвідношення
lp = 2k-1
= 2k
/ 2 > n/2, npp = 0, tl = n > lp,
і злиття ділянки довжиною lp та залишку довжиною n-lp дає впорядкований масив.
Аналіз алгоритму злиття.
Оцінимо складність наведеного алгоритму. При кожному виконанні тіла циклу while значення всіх елементів масиву копіюються в допоміжний масив і назад по одному разу, тобто виконується O(n) елементарних дій. Після останнього k-го кроку 2k<2n,
тобто k<1+logn, і це означає, що тіло циклу while виконується 1+ [log2
n[ =O(logn) разів. Отже, складність алгоритму оцінюється як O(nlogn).
Запишемо в таблицю значення виразів n, n(n-1)/2, n(1+[log2
n]) та округлене відношення r двох останніх:
| n |
n(n-1)/2 |
n(1+[log2
n]) |
r |
| 10 |
45 |
40 |
1 |
| 100 |
4950 |
700 |
7 |
| 1000 |
499500 |
10000 |
50 |
| 10000 |
49995000 |
140000 |
350 |
Як бачимо, кожне зростання n у 10 разів веде до зростання n(n-1)/2 та n(1+[log2n]) приблизно в 100 й 14 разів відповідно, і за n=10000 сортування злиттям виконується в сотні разів скоріше, ніж бульбашкове!
Зауважимо, що в наведеному алгоритмі сортування злиттям копіювання масиву в допоміжний указано лише для того, щоб ідею алгоритму було простіше сприйняти. Цей алгоритм нескладно переробити так, щоб замість копіювання в додатковий масив відбувалося злиття в нього упорядкованих ділянок. Отже, на кроках з номерами 1, 3, 5, … має відбуватися злиття в допоміжний масив, а на кроках 2, 4, 6, … – злиття в протилежному напрямку.
Завершуючи описання сортування злиттям, скажемо, що цей алгоритм є першим із ефективних алгоритмів сортування. У 1945 році його винайшов Джон фон Нейман, один із піонерів програмування.
Серйозним недоліком цього алгоритму є необхідність додаткового масиву такої ж довжини, як і в основного.
Реалізація завдань алгоритмом злиття на мові програмування Turbo Pascal. Нехай, маємо два впорядкованих масиви цілих значень, використовуючи метод злиття сформувати впорядкований по зростанню масив, що містить всі елементи даних масивів.
Program Zluttja;
uses crt;
const p=7; a=6;
var c:array[1..p] of real;
d:array[1..a] of real;
f:array[1..p+a] of real;
i,j,n:integer;
begin
clrscr;
writeln('vvedit pershy poslidovnist, kogen nastupnui bilshui poperednogo');
for i:=1 to p do readln(c[i]);
writeln('vvedit drygy poslidovnist, kogen nastupnui bilshui poperednogo');
for i:=1 to a do readln(d[i]);
clrscr;
writeln('-------------poslidovnist C-----------');
writeln('kilist elementiv = ', p);
for i:=1 to p do write(c[i]:4:2,' ');
writeln;
writeln('-------------poslidovnist D-----------');
writeln('kilist elementiv = ', a);
for i:=1 to a do write(d[i]:4:2,' ');
i:=1; j:=1; n:=0;
while (i<=p) and (j<=a) do
begin
inc(n);
if c[i]>d[j] then begin
f[n]:=d[j];
inc(j);
end
else begin
f[n]:=c[i];
inc(i);
end;
end;
while i<=p do
begin
inc(n); f[n]:=c[i]; inc(i);
end;
while j<=a do
begin
inc(n); f[n]:=d[j]; inc(j);
end;
writeln;
writeln('-------------------Sformovanui masuv-----------');
for i:=1 to p+a do write(f[i]:4:2,' ');
readln;
end.
2. Природне злиття
При використанні методу прямого злиття не приймається в увагу те, що вихідний файл може бути лише частково відсортованим, тобто містити впорядковані підпослідовності записів. Серією називається підпослідовність записів ai, a(i+1),..., aj така, що ak <= a(k+1) для всіх i <= k < j, ai < a(i-1) і aj > a(j+1). Метод злиття впорядкованих серій ґрунтується на розпізнаванні серій при розподілі і їхньому використанні при наступному злитті.
Як і у випадку прямого злиття, сортування виконується за кілька кроків, у кожному з яких спочатку виконується розподіл файлу A по файлах B і C, а потім злиття B і C у файл A. При розподілі розпізнається перша серія записів і записується у файл B, друга - у файл C і т.д. При злитті перша серія записів файлу B зливається з першою серією файлу C, друга серія B із другою серією C і т.д. Якщо перегляд одного файлу закінчується раніше, ніж перегляд іншого (через різне число серій), те залишок недопереглянутого файлу цілком копіюється в кінець файлу A. Процес завершується, коли у файлі A залишається тільки одна серія. Приклад сортування файлу показаний на малюнках 1 та 2.

Рис. 1. Перший крок
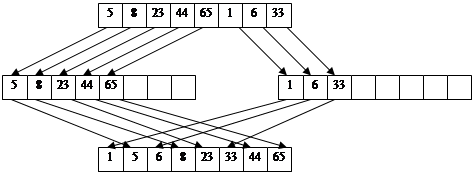
Рис. 2. Другий крок
Очевидно, що число читань/перезаписів файлів при використанні цього методу буде не гірше, ніж при застосуванні методу прямого злиття, а в середньому - краще. З іншого боку, збільшується число порівнянь за рахунок тих, які потрібні для розпізнавання кінців серій. Крім того, оскільки довжина серій може бути довільної, то максимальний розмір файлів B і C може бути близький до розміру файлу A.
Реалізація методу мові програмування Turbo Pascal. Нехай маємо типізований файл додатних цілочисельних даних, використовуючи метод злиття впорядкованих серій (природне злиття) відсортувати цей файл по зростанню.
Примітка: Для генерування початкового файлу тут і надалі в курсовій програмі використовується файл Generat.pas, що формує бінарні файли. Лістінг даної програми поданий в додатках.
Program Natural_sort;
type Item=record
key:longint;
end;
TFile=file of Item;
var
f0:TFile;
procedure merge(k:integer;var f1,f2,g1,g2:TFile);
var outSwitch:boolean;
Winner:integer;
Used:array[1..2] of integer;
Fin:array[1..2]of boolean;
current:array[1..2]of Item;
procedure GetItem(i:integer);
begin
if(Used[i]=k)or((i=1)and eof(f1))or((i=2)and eof(f2)) then Fin[i]:=True
else if i=1 then read(f1,Current[1])
else read(f2,Current[2]);
Used[i]:=Used[i]+1;
end;
begin
OutSwitch:=true;
rewrite(g1);rewrite(g2);
reset(f1);reset(f2);
while (not eof(f1)) or (not eof(f2)) do
begin
Used[1]:=0;Used[2]:=0;
Fin[1]:=false;Fin[2]:=false;
GetItem(1);GetItem(2);
while (not Fin[1])or(not Fin[2]) do
begin
if Fin[1] then Winner:=2
else if Fin[2] then Winner:=1
else if Current[1].key<Current[2].key then Winner:=1
else Winner:=2;
if OutSwitch then write(g1,Current[Winner])
else write(g2,Current[Winner]);
GetItem(Winner);
end;
OutSwitch:=not OutSwitch;
end;
close(g1);close(g2);
close(f1);close(f2);
end;
procedure MergeSort(var f0:TFile);
var f1,f2,g1,g2:TFile;
i,n,k:integer;buf:Item;
flag:boolean;
begin
Assign(f1,'F1Merge.itm');
Assign(f2, 'F2Merge.itm');
Assign(g1, 'G1Merge.itm');
Assign(g2,'G2Merge.itm');
rewrite(f1);rewrite(f2);
rewrite(g1);rewrite(g2);
reset(f0);
n:=0;
while not eof(f0) do
begin
read(f0,buf);
write(f1,buf);
inc(n);
if not eof(f0) then
begin
read(f0,buf);
write(f2,buf);
inc(n);
end;
end;
flag:=true;k:=1;
Close(f1);Close(f2);Close(f0);
n:=trunc(ln(n)/ln(2))+1;
for i:=1 to n do
begin
if flag then merge(k,f1,f2,g1,g2)
else merge(k,g1,g2,f1,f2);
flag:= not flag;
k:=k*2;
end;
rewrite(f0);reset(g1);reset(f1);
if not flag then
while not eof(g1) do
begin
read(g1,buf);
write(f0,buf);
end
else
while not eof(f1) do
begin
read(f1,buf);
write(f0,buf);
end;
Close(f0);Close(g1);Close(f1);
{erase(f1);erase(g1);erase(f2);erase(g2);}
end;
begin
assign(f0,'a-file.bin');
MergeSort(f0);
end.
3. Метод злиття впорядкованих серій
В основі методу зовнішнього сортування багатошляхового злиття (злитя впорядкованих серій) лежить розподіл серій вихідного файлу по m допоміжних файлах B1, B2,..., Bm і їхнє злиття в m допоміжних файлів C1, C2,..., Cm. На наступному кроці виробляється злиття файлів C1, C2,..., Cm у файли B1, B2,..., Bm і т.д., поки в B1 або C1 не утвориться одна серія. Графічно це можна зобразити наступним чином:

Рис. 3. Злиття впорядкованих серій
На малюнку 3 показаний простий приклад застосування сортування збалансованим багатошляховим злиттям. Він, звичайно, занадто тривіальний, щоб продемонструвати кілька кроків виконання алгоритму, однак достатній як ілюстрація загальної ідеї методу. Помітимо, що, як показує цей приклад, у міру збільшення довжини серій допоміжні файли з більшими номерами (починаючи з номера n) перестають використовуватися, оскільки їм «не дістається» ні однієї серії. Перевагою сортування збалансованим багатофазним злиттям є те, що число проходів алгоритму оцінюється як O(log n) (n - число записів у вихідному файлі), де логарифм береться по підставі n. Порядок числа копіювань записів - O(log n). Звичайно, число порівнянь не буде менше, ніж при застосуванні методу простого злиття.
Реалізація методу мовою програмування Turbo Pascal. Нехай маємо типізований файл додатних цілочисельних даних, використовуючи метод впорядкованих серій відсортувати цей файл по зростанню.
Program Vporjadkovane_zluttja;
const max=10000;
maxint=32767;
type
Item=record
key:integer;
end;
TFile=file of Item;
var
f0:TFile;
procedure NMerge(k:integer;var f1,f2,f3,f4,g1,g2,g3,g4:TFile);
var outSwitch:1..4;
Winner:integer;
Used:array[1..4] of integer;
Fin:array[1..4]of boolean;
Current:array[1..4]of Item;
Tree:array[1..7]of Item;
History:array[1..7]of integer;
procedure CompareTree;
begin
if Tree[7].key<Tree[6].key then
begin
Tree[3]:=Tree[7];
History[3]:=History[7];
end
else
begin
Tree[3]:=Tree[6];
History[3]:=History[6];
end;
if Tree[5].key<Tree[4].key then
begin
Tree[2]:=Tree[5];
History[2]:=History[5];
end
else
begin
Tree[2]:=Tree[4];
History[2]:=History[4];
end;
if Tree[3].key<Tree[2].key then
begin
Tree[1]:=Tree[3];
History[1]:=History[3];
end
else
begin
Tree[1]:=Tree[2];
History[1]:=History[2];
end;
end;
procedure NGetItem(i:integer);
begin
if(Used[i]=k)or((i=1)and eof(f1))or((i=2)and eof(f2))or((i=3)and eof(f3))or((i=4)and eof(f4)) then
begin
Fin[i]:=True;
Tree[8-i].key:=MaxInt;
end
else
begin
case i of
1:read(f1,Current[1]);
2:read(f2,Current[2]);
3:read(f3,Current[3]);
4:read(f4,Current[4]);
end;
Tree[8-i]:=Current[i];
Used[i]:=Used[i]+1;
end;
CompareTree;
end;
procedure MakeTree;
var q:integer;
begin
if not eof(f1) then
begin
read(f1,Tree[7]);
History[7]:=1;
Current[1]:=Tree[7];
end;
if not eof(f2) then
begin
read(f2,Tree[6]);
History[6]:=2;
Current[2]:=Tree[6];
end;
if not eof(f3) then
begin
read(f3,Tree[5]);
History[5]:=3;
Current[3]:=Tree[5];
end;
if not eof(f4) then
begin
read(f4,Tree[4]);
History[4]:=4;
Current[4]:=Tree[4];
end;
CompareTree;
end;
begin
OutSwitch:=1;
rewrite(g1);rewrite(g2);
rewrite(g3);rewrite(g4);
reset(f1);reset(f2);
reset(f3);reset(f4);
while (not eof(f1)) or (not eof(f2))or (not eof(f3))or (not eof(f4)) do
begin
Used[1]:=1;Used[2]:=1;Used[3]:=1;Used[4]:=1;
Fin[1]:=false;Fin[2]:=false;Fin[3]:=false;Fin[4]:=false;
MakeTree;
while Tree[1].key<MaxInt do
begin
Winner:=History[1];
case OutSwitch of
1:write(g1,Current[Winner]);
2:write(g2,Current[Winner]);
3:write(g3,Current[Winner]);
4:write(g4,Current[Winner]);
end;
NGetItem(Winner);
end;
if OutSwitch=4 then OutSwitch:=1
else inc(OutSwitch);
end;
Close(g1);Close(g2);
Close(f1);Close(f2);
Close(g3);Close(g4);
Close(f3);Close(f4);
end;
procedure NMergeSort(var f0:TFile);
var f1,f2,f3,f4,g1,g2,g3,g4:TFile;
i,n,k:integer;buf:Item;
flag:boolean;
begin
assign(f1,'F1Merge.itm');
assign(f2,'F2Merge.itm');
assign(f3,'F3Merge.itm');
assign(f4,'F4Merge.itm');
assign(g1,'G1Merge.itm');
assign(g2,'G2Merge.itm');
assign(g3,'G3Merge.itm');
assign(g4,'G4Merge.itm');
rewrite(f1);rewrite(f2);
rewrite(f3);rewrite(f4);
rewrite(g1);rewrite(g2);
rewrite(g3);rewrite(g4);
reset(f0);
n:=0;
while not eof(f0) do
begin
read(f0,buf);
write(f1,buf);
inc(n);
if not eof(f0) then
begin
read(f0,buf);
write(f2,buf);
inc(n);
end;
if not eof(f0) then
begin
read(f0,buf);
write(f3,buf);
inc(n);
end;
if not eof(f0) then
begin
read(f0,buf);
write(f4,buf);
inc(n);
end;
end;
flag:=true;k:=1;
Close(f1);Close(f2);Close(f0);
Close(f3);Close(f4);
n:=trunc(ln(n)/ln(4))+1;
for i:=1 to n do
begin
if flag then NMerge(k,f1,f2,f3,f4,g1,g2,g3,g4)
else NMerge(k,g1,g2,g3,g4,f1,f2,f3,f4);
flag:= not flag;
k:=k*4;
end;
rewrite(f0);reset(g1);reset(f1);
if not flag then
while not eof(g1) do
begin
read(g1,buf);
write(f0,buf);
end
else
while not eof(f1) do
begin
read(f1,buf);
write(f0,buf);
end;
Close(f0);Close(g1);Close(f1);
erase(f1);erase(g1);erase(f2);erase(g2);
erase(f3);erase(g3);erase(f4);erase(g4);
end;
begin
assign(f0,'a-file.bin');
NMergeSort(f0);
end.
4. Багатофазне злиття
Розглядувані вище прийоми дають змогу створити більш ефективний алгоритм, ніж попередні. Так, ми бачили що при збалансованому злитті зникають операції простого копіювання, оскільки розподілення і злиття об’єднані в одну фазу. Нове вдосконалення заклечається в тому, що коли відмовитися від строгого поняття проходу, то саме поняття можна тлумачити і реалізовувати по іншому. Цей метод був створений Р.Л. Гілстадом і названий багатофазним сортуванням.
Спочатку проілюструємо його на прикладі роботи із трьома файлами. В кожний момент елементи зливаються із двох файлів у третій. Як тільки один із вхідних файлів стане вичерпаним, він стає вихідним для злиття з іншим файлом, який ще не вичерпався і з тим, що якого був вихідним.
Оскільки ми знаємо, що n серій на кожному вхідному файлі перетворюються в n серій на вихідному, нам потрібно тільки вести список числа серій на кожному файлі.
Зрозуміло, що принципова структура багатофазного злиття основною частиною програми n-шляхового злиття: наявний внутрішній цикл, в тілі якого зливаються серії, поки не будуть вичерпані всі вхідні дані, внутрішній цикл, в тілі якого зливаються по одній серії з кожної вхідної лєнти (файлу), і сам внутрішній цикл, в тілі якого вибирається начальний ключ і елемент передається в вихідний файл. Принципові відмінності в наступному:
1. На кожному проході маємо тільки один вихідний фай замість n/2.
2. Замість перемикання n/2 вхідних і n/2 вихідних файлів після кожного проходу файли передуються. Це досягається з допомогою карти файлових індексів t.
3. Число вхідних файлів міняється від серії до серії; спочатку кожної серії воно визначається по індексам фіктивних серій. Якщо >0 для всіх і, то n-1 фіктивних серій зливаються в одну фіктивну серію при допомозі простого збільшення індекса вихідного файлу. В протилежному випадку зі всіх файлів, у яких індекс =0, зливається по одній серії, а для всіх решти файлів індекс зменшується, що означає вилучення однієї фіктивної серії. Число вхідних файлів ми позначимо через k.
4. Неможливо встановити закінчення фази при допомозі стану закінчення файлу (n- 1) лєнти, оскільки можуть знадобитися подальші злиття, в яких залучені фіктивні серії з цієї ленти. Замість цього теоретично необхідне число серій визначається на коефіцієнту ai
Коефіцієнти ai
були обраховані на фазі розподілення; тепер їх можна обрахувати в зворотному порядку.
Реалізація методу багатофазного злиття на Turbo Pascal. Нехай маємо файл цілих чисел, відсортувати його використовуючи багатофазне злиття.
Program polysort;
{багатофазне сортування з n - лентами}
Const n=6; {число лент}
Type item = record
Key:integer;
End;
Tape = file of item;
Tapeno = 1..n;
Var leng, rand: integer; {використовується для формування файлу}
Eot: Boolean;
Buf: item;
F0: tape; {f0 – вхідна лента із випадковими числами }
F: array [1..n] of tape;
Procedure List (var f: tape; n:tapeno);
Var z: integer;
Begin z:=0;
Writeln(‘TAPE’,n:2);
While not eof(f) do
Begin read(f,buf); write(output,buf.key: 5); z:=z+1;
If z=25 then
Begin writeln(output); z:=0
End;
End;
If z<>0 then writeln(output); reset(f);
End; {LIST}
Procedure Pholyphasesort;
Var I,j,mx,tn:tapeno;
K,level: integer;
A,d: array [tapeno] of integer;
{a[j] – ідеальне число серій на ленті }
{d[j] – число фіктивних серій на ленті}
Dn, x, min, z:integer;
Last: array [tapeno] of integer;
{last[j] – ключ кінцевої серії на ленті}
T,ta: array [tapeno] of tapeno;
{карти номерів ленти}
Procedure selecttape;
Var i: tapeno; z:integer;
Begin
If d[j]<d[j+1] then j:=j+1 else
Begin if d[j]=0 then
Begin level:=level+1; z:=d[1];
For i:=1 to n-1 do
Begin d[i]:=z+a[i+1]-a[i]; a[i]:=z+a[i+1]
End;
End;
J:=1;
End;
D[j]:=d[j]-1;
End;
Procedure copyrun;
Begin {перепис однієї серії з f0 на ленту}
Repeat read(f0,buf); write(f[j],buf);
Until eof(f0) or (buf.key>f0.key);
Last[j]:=buf.key;
End;
Begin {розподіл початкових серій}
For i:=1 to n-1 do
Begin a[i]:=1; d[i]:=1; rewrite(f[i]);
End;
Level:=1; j:=1; a[n]:=0; d[n]:=0;
Repeat selecttape; copyrun
Until eof(f0) or (j=n-1);
While not eof(f) do
Begin selecttape;
If last[j]<=f0.key then
Begin {продовження попередньої серії}
Copyrun;
If oef(f0) then d[j]:=d[j]+1 else copyrun
End
Else copyrun
End;
For i:=1 to n-1 do reset(f[i]);
For i:=1 to n do t[i]:=I;
Repeat {злиття з t[1]…t[n-1] на t[n]}
Z:=a[n-1]; d[n]:=0; rewrite(f[t[n]]);
Repeat k:=0; {злиття однієї серії}
For I:=1 to n-1 do
If d[i]>0 then d[i]:=d[i]-1 else
Begin k:=k+1; ta[k]:=t[i];
End;
If k=0 then d[n]:=d[n]+1 else
Begin {злиття одного дійсного відрізка із t[1]…t[k]}
Repeat i:=1; mx:=1;
Min:=f[ta[1]].key;
While i<k do
Begin I:=i+1; x:=f[ta[i]].key;
If x<min then
Begin min:=x; mx:=i
End;
End;
Read(f[ta[mx]],buf);eot:=eof(f[ta[mx]]);
Write(f[t[n]],buf);
If (buf.key>f[ta[mx]].key)or eot then
Begin Ta[mx]:=ta[k]; k:=k-1
End
Until k=0
End;
Z:=z-1;
Until z=0;
Reset(f[t[n]]); list(f[t[n]],t[n]);
tn:=t[n]; dn:d[n]; z:=a[n-1];
for i:=n downto 2 do
begin t[i]:=t[i-1]; d[i]:=d[i-1]: a[i]:=a[i-1] –z
end;
t[1]:=tn; d[1]:=dn; a[1]:=z;
list (f[t[1]],t[1]); level:=level -1;
until level=0;
end {polyphasesort};
begin
leng:=200; rand:=7789;
repeat rand:=(131071*rand) mod 2147483647;
buf.key:=rand div 2147484; write(f0,buf);
leng:=leng-1
until leng=0;
reset(f0); list(fo,1);
polyphasesort;
end.
Висновки
Як відомо, існує дуже багато методів сортування масивів, які поділяються на прямі і швидкі. Проте, їх практично не можливо застосувати по роботі із великими файлами, коли об’єм даних перевищує об’єм оперативної пам’яті. Саме тому, метою даної курсової програми було розглянути існуючі методи сортування файлів.
Так, ми розглянули найбільш відомі широкому загалу методи: простого злиття, метод природного злиття, метод збалансованого злиття впорядкованих серій та багатофазного злиття.
Оскільки ми не ставили собі за мету вивчити можливість та переваги тих чи інших методів сортування у конкретних задачах, то із поставленою метою, а саме із вивченням і реалізацію найбільш використовуваних у сучасному програмуванні алгоритмів сортування файлів ми справилися повністю.
У відповідності до мети та завдання курсової роботи були виконані наступні кроки:
1. Було проведено детальний аналіз літератури та електронних джерел за темою «сортування файлів та послідовностей», це дало змогу сформувати як теоретичні основи, так і зробити передбачення щодо створення програм демонстраційного характеру.
2. До вибору мови програмування, щодо реалізації даних методів ми підійшли з тієї точки зору, що б вона програма, яку ми б написали була зрозуміла широкому загалу, а саме Turbo Pascal. Вибір даної мови програмування був обумовлений тим, що вона найбільш підходить для навчальних цілей. Оскільки в школах і вузах початки програмування і алгоритмізацію показуються саме з допомогою Turbo Pascal. Вибір цієї мови програмування був зумовлений ще і її гнучкістю і простотою в застосуванні і розумінні. У програмах було зроблено коментарі, які роблять їх більш зрозумілими для розуміння;
3. У курсовій роботі ми не проводили сортування файлів, що б містили складні структури даних. Це пов’язано із тим, що ми виклали найбільш використовувані алгоритми, їх математичні моделі і вже знаючи ці методи, можна досить просто перевести їх використання і подальше удосконалення на практиці.
4. Зрозуміло, що хоча ми і розглянули найбільш відомі методи сортування файлів, існує ще безліч інших способів їх удосконалення. Так наприклад, при багатофазному злитті сортування у вже розбитих серіях можна проводити і за допомогою статичних методів сортування, наприклад за допомогою дерева, чи швидкого сортування, це також пришвидшить роботу алгоритму.
Отже, виконуючи курсову роботу, ми вивчили розділ програмування «сортування послідовностей і файлів», провели аналіз швидкодії важкості реалізації найбільш використовуваних на практиці алгоритмів сортування, навели графічне представлення операцій сортування та створили робочі програми, які наявно демонструють роботу цих методів.
Дану курсову роботу, на нашу думку, можна використовувати в курсі вивчення основних методів і алгоритмів сортування та пошуку даних.
Література
1. Turbo Pascal – Издательская група К.: ВНV, 2000. – 320 с.
2. Абрамов В.Г. Введение в язык Pascal: Учебное пособие для студентов вузов по специальности Прикладная математика. – М.: Наука, 1988. – 200 с.
3. Абрамов С.А., Зима Е.В. Начала программирования на языке Pascal. - М.: Наука, 1987. – 126 с.
4. Андреева Е., Фалина И. Системы счисления и компьютерная арифметика. М.: Лаборатория базовых знаний, 2000. – 201 с.
5. Ахо А.А., Хопкрофт Д.Э., Ульман Д.Д. Структуры данных и алгоритмы. М.: “Вильямс”, 2000. – 163 с.
6. Вирт Н. Алгоритмы и структуры данных. M.: Мир, 1989. – 142 с.
7. Власик А.П. Практикум з програмування в середовищі Turbo Pascal. Ч 1.- Рівне: НУВГП, 2005. – 179 с.
8. Глушаков С.В. Программирование на Visual C++. – М.: АСТ; Х.: Фоліо, 2003. – 726 с.
9. Грис Д. Наука программирования. M.: Мир, 1984. – 230 с.
10. Джонс Ж., Харроу К. Решение задач в системе Турбо-Паскаль/ Перевод с английского Улановой, Широкого. – М.: Финансы и статистика, 1991. – 709 с.
11. Зуев Е. А. Язык программирования Турбо Паскаль 6.0, 7.0. – М.: Радио и связь, 1993. – 150 с.
12. Кнут Д.Э. Искуство програмирования, том 3. Поиск и сортировка, 3-е изд.: Пер. с англ.: Уч. Пос. – М.:Издательский дом «Вильямс», 2000. – 750 с.
13. Кнут Д.Э. Искуство програмирования, том 3. Поиск и сортировка, 3-е изд.: Пер. с англ.: Уч. Пос. – М.:Издательский дом «Вильямс», 2000. – 750 с.
14. Ковалюк Т.В. Основи програмування. Київ: Видавнича група ВНV, 2005. – 385 с.
15. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы. Построение и анализ. М.: МЦНМО, 2000. – 93 с.
16. Культин Н. Б. Программирование в Turbo Pascal 7.0 и Delphi. - Санкт- петербург,1999.
17. Львов М. С., Співаковський О. В. Основи алгоритмізації та програмування. Херсон, 1997.
18. Марченко А.И., Марченко Л.А. Программирование в среде Turbo Pascal 7.0. К.: ВЕК, 2000. – 441 с.
19. Окулов С.M. Сортировка и поиск. “Информатика”, №35, 2000. – 73 с.
20. Перминов О. Н. Язык программирования Pascal. – М.: Радио и связь,1989. – 205 с.
21. Фаронов В. В. TurboPascal 7.0. Начальный курс. – М.: “Нолидж”, 2000.
22. Шень А. Программирование: теоремы и задачи. М.: МЦНМО. – 205 с.
23. Щедріна О.І. Алгоритмізація та програмування процедур обробки інформації. К., 2001. – 240 с.
Додаток 1
Лістінг програми генерації початкових бінарних файлів.
program Generat;
type
item=record
key:integer;
end;
filetype=file of item;
var
a,b:file of item;
i:longint;
a_len:integer;
b_len:integer;
x:item;
begin
assign (a,'a-file.bin');
assign (b,'b-file.bin');
write ('Введіть довжину файлу A: ');
readln (a_len);
write ('Введіть довжину файлу B: ');
readln (b_len);
rewrite (a);
randomize;
i:=0;
while i<=a_len do
begin
x.key:=random(a_len);
write(a,x);
inc(i);
end;
close (a);
rewrite (b);
i:=0;
while i<=b_len do
begin
x.key:=random(b_len);
write (b,x);
inc(i);
end;
close (b);
writeln ('Файли утоврені коректно');
readln;
end.
|