РЯЗАНСКОЕ
ВЫСШЕЕ ВОЗДУШНО-ДЕСАНТНОЕ КОМАНДНОЕ
ДВАЖДЫ КРАСНОЗНАМЕННОЕ УЧИЛИЩЕ
ИМЕНИ ГЕНЕРАЛА АРМИИ МАРГЕЛОВА В.Ф.
Кафедра высшей математики и теоретической механики
КУРСОВАЯ РАБОТА
ЗАДАЧИ ОПТИМИЗАЦИИ
Выполнил курсант: Валуйкин Александр Владимирович
4 взвода 8 роты
Руководитель работы: Щукина Наталья Васильевна
Рязань – 2001 г.
СОДЕРЖАНИЕ
Введение................................................................................................................................. 3
§1. ПОСТАНОВКА ЗАДАЧ ОПТИМИЗАЦИИ.................................................................... 5
§2 ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ....................................................... 7
§3 АНАЛИТИЧЕСКИЙ МЕТОД ОПТИМИЗАЦИИ......................................................... 13
ЗАКЛЮЧЕНИЕ........................................................................................................................ 15
ЛИТЕРАТУРА.......................................................................................................................... 16
Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного или заданного критерия. На практике оказывается, что в большинстве случаев понятие «наилучший» может быть выражено количественными критериями – минимум затрат, минимум времени, максимум прибыли и т.д. Поэтому возможна постановка математических задач отыскания оптимального (optimum – наилучший) результата, так как принципиальных различий в отыскании наименьшего или наибольшего значения нет. Задачи на отыскание оптимального решения называются задачами оптимизации. Оптимальный результат, как правило, находится не сразу, а в результате процесса, называемого процессом оптимизации. Применяемые в процессе оптимизации методы получили название методов оптимизации. Чтобы решить практическую задачу надо перевести ее на математический язык, то есть составить ее математическую модель.
Реклама

Математическая модель представляет собой стройную и глубокую совокупность знаний о математических моделях со своими проблемами, с собственными путями развития, обусловленными внутренними и внешними причинами и задачами. Математика дает удобные и плодотворные способы описания самых разнообразных явлений реального мира и тем самым выполняет в этом смысле функцию языка. Эту роль математики прекрасно осознавал Галилей, сказавший: «Философия написана в грандиозной книге – Вселенной, которая открыта нашему пристальному взгляду. Но понять эту книгу может лишь тот, кто научился понимать ее язык и знаки, которыми она изложена. Написана же она на языке математики».
Итак, математика – это область человеческого знания, в которой изучаются математические модели.
Часто в математической модели требуется найти наибольшее или наименьшее значение некоторой функции на некотором множестве, то есть решить задачу оптимизации. Методов решения задач оптимизации достаточно много. Некоторые из них рассматривались при отыскании экстремальных значений функций одной и многих вещественных переменных. Кроме точных методов широко используются и приближенные, например, метод дихотомии и т.д.
Знание методов нахождения оптимального решения позволяет инженеру и офицеру выбирать наиболее эффективные и самые экономичные способы эксплуатации и ремонта машин, находить оптимальные решения тактических задач.
В курсовой работе по методам оптимизации предлагается две задачи: задача линейного программирования и общая задача оптимизации, решаемая аналитическим методом.
На протяжении всей своей эволюции человек, совершая те или иные деяния, стремился вести себя таким образом, чтобы результат, достигаемый как следствие некоторого поступка, оказался в определенном смысле наилучшим. Двигаясь из одного пункта в другой, он стремился найти кратчайший среди возможных путь. Строя жилище, он искал такую его геометрию, которая при наименьшем расходе топлива, обеспечивала приемлемо комфортные условия существования. Занимаясь строительством кораблей, он пытался придать им такую форму, при которой вода оказывала бы наименьшее сопротивление. Можно легко продолжить перечень подобных примеров.
Наилучшие в определенном смысле решения задач принято называть оптимальными
. Без использования принципов оптимизации в настоящее время не решается ни одна более или менее сложная проблема. При постановке и решении задач оптимизации возникают два вопроса: что и как оптимизировать?
Реклама

Ответ на первый вопрос получается как результат глубокого изучения проблемы, которую предстоит решить. Выявляется тот параметр, который определяет степень совершенства решения возникшей проблемы. Этот параметр обычно называют целевой функцией
или критерием качества
. Далее устанавливается совокупность величин, которые определяют целевую функцию. Наконец, формулируются все ограничения, которые должны учитываться при решении задачи. После этого строится математическая модель, заключающаяся в установлении аналитической зависимости целевой функции от всех аргументов и аналитической формулировки сопутствующих задаче ограничений. Далее приступают к поиску ответа на второй вопрос.
Итак, пусть в результате формализации прикладной задачи установлено, что целевая функция 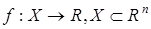 , где множество Х – обобщение ограничений, его называют множеством допустимых решений. Существо проблемы оптимизации заключается в поиске на множестве Х – множестве допустимых решений такого решения , где множество Х – обобщение ограничений, его называют множеством допустимых решений. Существо проблемы оптимизации заключается в поиске на множестве Х – множестве допустимых решений такого решения 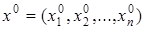 , при котором целевая функция f
достигает наименьшего или наибольшего значения. , при котором целевая функция f
достигает наименьшего или наибольшего значения.
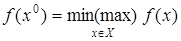
Составной частью методов оптимизации является линейное программирование.
Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.
Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам линейного программирования посвящено много работ зарубежных и прежде всего американских ученых.
Задача линейного программирования состоит в следующем: максимизировать (минимизировать) линейную функцию
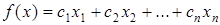 , где , где 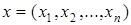
при ограничениях
(*)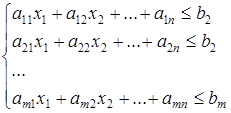
причем все 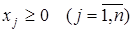
Замечание
. Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).
Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.
Итак, надо максимизировать функцию 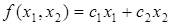 и удовлетворяющей системе ограничений. и удовлетворяющей системе ограничений.
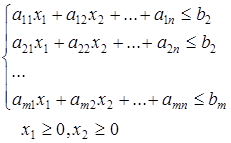
Обратимся к одному из неравенств системы ограничений.
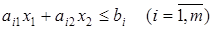
С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой 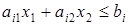 , либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того, чтобы выяснить это, надо проверить какая из них содержит точку ( , либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того, чтобы выяснить это, надо проверить какая из них содержит точку (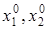 ). ).
Замечание 2
. Если 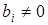 , то проще взять точку (0;0). , то проще взять точку (0;0).
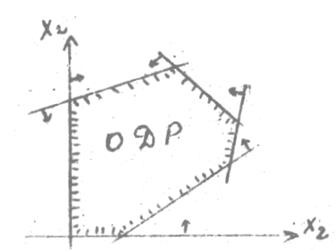 Условия неотрицательности Условия неотрицательности 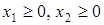 также определяют полуплоскости соответственно с граничными прямыми также определяют полуплоскости соответственно с граничными прямыми 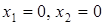 . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы – это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы – это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую 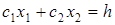 (где h
–
некоторая постоянная). Чаще всего берется прямая (где h
–
некоторая постоянная). Чаще всего берется прямая 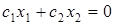 . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции
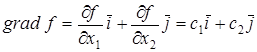
Вектор 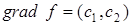 в каждой точке перпендикулярной прямой в каждой точке перпендикулярной прямой 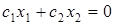 , поэтому значение f
будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой , поэтому значение f
будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой  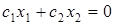 проводим прямые, смещаясь в направлении градиента (антиградиента). проводим прямые, смещаясь в направлении градиента (антиградиента).
Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.
Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:
1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор 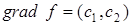 . .
5. Строят прямую 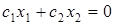 . .
6. Строят параллельные прямые 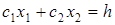 в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве. в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.
7. Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
Пример 1.
Два больших войсковых соединения 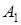 и и 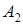 к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции к новому месту дислокации перевозятся по железной дороге. Для их погрузки выделяются три станции 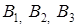 , с различными возможностями. Перевозка соединений осуществляется с соблюдением следующих ограничений: , с различными возможностями. Перевозка соединений осуществляется с соблюдением следующих ограничений:
1. Количество перевозимых частей в соединении 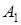 равно 6, а в равно 6, а в 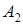 –9. –9.
2. Каждая станция может принять определенное количество частей: 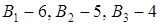 . .
3. На погрузку одной части станции затрачивают различное время (в сутках), которое указано в таблице.
| Соединения |
Станция погрузки |
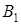 |
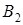 |
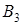 |
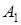
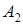
|
3,0
4,5
|
4,0
6,5
|
2,5
3,5
|
Определить оптимальный вариант распределения частей по станциям погрузки, исходя из минимума суммарных затрат времени на погрузку.
Решение.
Решение штабов соединений состоит в распределении частей по станциям погрузки. Обозначим через 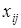 число частей i
-
го соединения (i
=1,2) на j
-
ой станции (j
=
1, 2, 3). число частей i
-
го соединения (i
=1,2) на j
-
ой станции (j
=
1, 2, 3).
Мы можем записать:
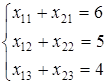
количество частей соединений на станциях погрузки 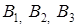 соответственно. соответственно.
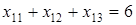 - количество частей соединения - количество частей соединения 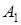 на местах погрузки. на местах погрузки.
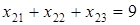 - количество частей соединения - количество частей соединения 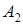 на местах погрузки. на местах погрузки.
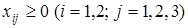
Общая сумма затрат времени (в сутках) на погрузку есть
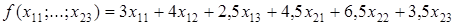
В этой задаче 6 переменных, но мы можем свести к двум.
Пусть 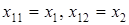
Тогда 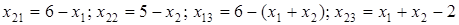
Целевая функция имеет вид
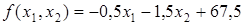
Итак, надо найти 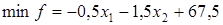 при ограничениях: при ограничениях:
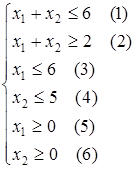
которая решается графически
Возьмем прямую 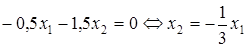 и начнем строить параллельные ей в направлении антиградиента, где и начнем строить параллельные ей в направлении антиградиента, где 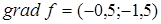 . .
Последняя вершина многоугольника решений есть точка С
, получаемая пересечением прямых (1) и (4). Решая, получим С
(1;5).
Итак, оптимальные значения будут следующими: 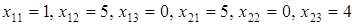 , а общие затраты времени , а общие затраты времени 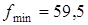 (суток). (суток).
Пусть дана целевая функция 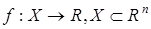 . .
Для нахождения наибольшего и наименьшего значения функции и (одной) вещественных переменных надо найти критические точки, в которых частные производные (производная) функции f
по всем переменным обращается в 0. Кроме того, надо исследовать точки границы, если она принадлежит области определения. Среди них выбрать значения, где f
принимает наибольшее и наименьшее значение.
 Пример 2.
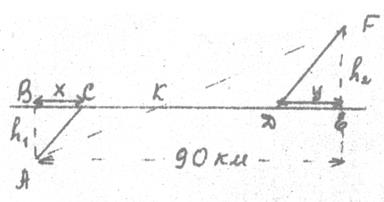
Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги Пример 2.
Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги 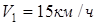 , по дороге , по дороге 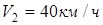 , за дорогой , за дорогой 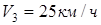 . Удаление от дороге пункта А равно . Удаление от дороге пункта А равно 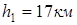 , пункта F , пункта F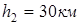 . Расстояние между точками В и Е равно L = 90 км
. . Расстояние между точками В и Е равно L = 90 км
.
Составим математическую модель, то есть найдем функцию цели. Нас интересует время. Время выдвижения из пункта А в пункт F.
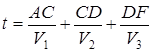
ВС = х км
; DE = yкм
; АС = 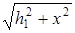
CD = L – x – y; DF = 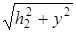 
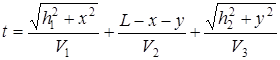
Составим функцию цели, которая зависит от двух переменных 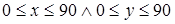
Найдем критические точки
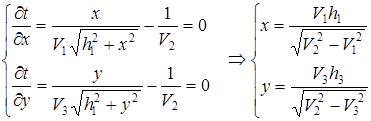
При данных условиях 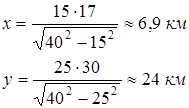
Найдем значение t
при полученных x
и y
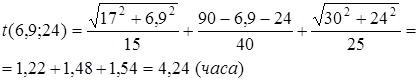
При вычислении значения t
на границе, значения получаются больше, чем 4,24 часа. Следовательно, оптимальное решение будет при
х
= 6,9 км
, у
= 24 км
, 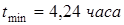 . .

Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, управления войсками, углублением общественного разделения труда, предъявлением высоких требований к методам планирования хозяйственного и военного руководства. В этих условиях только научный подход к руководству хозяйственной жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Научного подхода требует и решение тактических и стратегических задач, руководство военными операциями.
В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение как в экономических исследованиях и планировании, так и в решении военных тактических задач. Этому способствует развитие таких разделов математики как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен большой опыт постановки и решения экономических и тактических задач с помощью математических методов. Особенно успешно развиваются методы оптимального управления. Ярким примером применения современных математических методов является война Америки с Ираком и «Буря в пустыне». Там быстро развивается экономика и производство, где широко используются математические методы.
1. Тихонов А. Н., Костомаров Л. П. Вводные лекции по прикладной математике. М., Наука, 1984.
2. Кудрявцев Е. Н. Исследования операций в задачах, алгоритмах и программах. М., Наука, 1982.
3. Кузнецов Ю. Н., Кузубов В. И., Волощеноко А. В. Математическое программирование. М., Высшая школа, 1980.
4. Ильин В. А., Позняк Э. Г. Основы математического анализа. М., Наука, 1979.
|