Задача 1
За год на предприятии были выпущены семь партий продукции, для каждой из которых были определены издержки. Вычислить сумму издержек для следующего плана выпуска.
линейный экономический моделирование
Таблица 1.1.Данные о планируемом выпуске изделий
| ед.прод. тыс.шт. |
затраты, руб. |
| 2,2 |
? |
| 3,9 |
? |
| 5,5 |
? |
Таблица 1.2.Данные о выпущенных партиях
| ед.прод.тыс.шт. |
затраты, руб. |
| 1 |
30 |
| 2 |
70 |
| 4 |
150 |
| 3 |
100 |
| 5 |
170 |
| 6 |
215 |
| 8 |
290 |
Задача относится к разделу Парная регрессия, т.к. в ней даны один независимый параметр (единицы продукции, обозначим как х) и зависимый параметр (затраты, обозначим у).Прежде чем выбирать вид аппроксимирующей зависимости следует представить исходные данные графически.
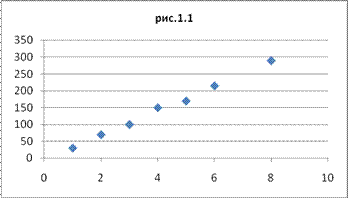
Предполагаем линейную зависимость между х и у
Y=a+bx
Для определения параметров a,b используем метод наименьших квадратов
∑( y –(a+bx))² → min
Функция минимальна, если равны нулю ё, частные производные по параметрам т.е.:
y’a = ∑ (2( y-abx)(-1))=0
y’b = ∑ (2 ( y-a-bx)(-x))=0
или
na+b∑x =∑y,
a ∑x +b ∑x² =∑xy (1)
Система уравнений (1) однозначно определяет параметры a и b – это система двух уравнений с двумя неизвестными. Все остальные величины можно определить из исходных данных :
n- количество исходных точек,
∑x ∑y - суммарные значения параметров х и у по всем точкам,
∑xy - суммарное значение произведения параметров,
∑x²- суммарное значение квадрата величины х.
Рассчитаем коэффициенты линейного уравнения парной регрессии:
Σx^2 = (x^2) - cp –(xcp)^2
b= (cp(y*x) – cp(y)*cp(x))/(σx^2) (2)
a = cp( y) - b*cp(x)
Где индекс cp обозначает среднее значение данной величины, т.е. суммарное значение данной величины надо разделить на n.
Составим таблицу в редакторе Excel.
Таблица 1.3
| n |
x |
y |
xy |
x^2 |
| 1 |
1 |
30 |
30 |
1 |
| 2 |
2 |
70 |
140 |
4 |
| 3 |
4 |
150 |
600 |
16 |
| 4 |
3 |
100 |
300 |
9 |
| 5 |
5 |
170 |
850 |
25 |
| 6 |
6 |
215 |
1290 |
36 |
| 7 |
8 |
290 |
2320 |
64 |
| итого |
29 |
1025 |
5530 |
155 |
| среднее |
4,14 |
146,43 |
790,00 |
22,14 |
| σ² |
4,98 |
Используя из табл. 1.3, получаем следующую систему уравнений:
7a+29b=1025
29a+155b=5530
Решаем систему уравнений методом последовательных исключений переменных или по формуле (2) и определяем коэффициенты
a= -6.127
b= 36.824
линейное уравнение запишем в виде
y=-6.127+36.824x (3)
Для варианта х=2,у=9 ,z =5 рассчитываем затраты
Таблица 1.4
| ед.прод. тыс.шт. |
затраты, руб. |
| 2,2 |
74,89 |
| 3,9 |
137,49 |
| 5,5 |
196,41 |
Используя пакет прикладных программ (ППП) статистическая функция ЛИНЕЙНАЯ и графические результаты (добавить линию тренда) проверим полученные результаты.
Реклама

Таблица 1.5
| 36,824 |
-6,127 |
| 0,987 |
4,64432 |
| 0,9964 |
5,82708 |
| 1392 |
5 |
| 47266 |
169,775 |
Рис.1.2.
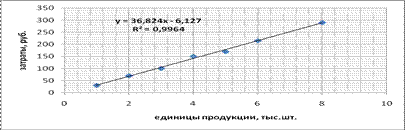
Кроме того, по найденному уравнению линейной регрессии (3) проведем расчет величин у, сравним их с заданными, т.е. рассчитаем отклонения и определим их суммарное отклонение, которое должно быть равно нулю. Результаты приведем в табл. 1.6.
Таблица 1.6
| n |
x |
y |
xy |
y² |
x² |
y расч |
y-y расч |
| 1 |
1 |
30 |
30 |
900 |
1 |
30,7 |
-0,7 |
| 2 |
2 |
70 |
140 |
4900 |
4 |
67,5 |
2,5 |
| 3 |
4 |
150 |
600 |
22500 |
16 |
141,2 |
8,8 |
| 4 |
3 |
100 |
300 |
10000 |
9 |
104,3 |
-4,3 |
| 5 |
5 |
170 |
850 |
28900 |
25 |
178,0 |
-8,0 |
| 6 |
6 |
215 |
1290 |
46225 |
36 |
214,8 |
0,2 |
| 7 |
8 |
290 |
2320 |
84100 |
64 |
288,5 |
1,5 |
| итого |
29 |
1025 |
5530 |
197525 |
155 |
0,0 |
Выводы:
1. Решена задача парной регрессии методом наименьших квадратов.
2. Получены коэффициенты в линейном уравнении y=-6.127+36.824x и рассчитан возможный домашний вариант.
3. Результаты проверены с помощью ППП и линии тренда.
Задача 2.
По семи территория Уральского района за 1995 г. Изе6стны значения двух признаков (табл.2.1)
Таблица 2.1
| район |
расходы на покупку продовольственных товаров в общих расходах, % у |
среднедневная заработная плата одного работающего, руб.,х |
| Удмуртская респ. |
68,8 |
45,1 |
| Свердловская обл. |
61,2 |
59 |
| Башкортостан |
59,9 |
57,2 |
| Челябинская обл. |
56,7 |
61,8 |
| Пермская обл. |
55 |
58,8 |
| Курганская обл. |
54,3 |
47,2 |
| Оренбургская обл. |
49,3 |
55,2 |
Требуется определить параметры парной регрессии для следующих функции: линейной степенной показательной, равносторонней геперболы и параболы методом наименьших квадратов (МНК). Составить прогноз величины у для некоторого х например для х=1.1 (х) min. Дать графическую интерпретацию результатов, использовать ППП для решения статистических задач сделать выводы.
К исходным данным добавим ещё одну пару значений х,у, связанную с порядковым номером по журналу и количеством студентов в группе, по формулам:
x8=xmin+((xmax-xmin)/Nсум)*Ni
y8=ymin+((ymax-ymin)/Nсум)*Ni
где, Ni–порядковый номер по журналу, Nсум- количество студентов в группе, min, max– минимальная и максимальная величины х и у по таблице 2.1.
после этого составляем таблицу 2.2 и рассчитываем все параметры для решения системы уравнений:
na+b∑x =∑y (4)
a∑x+b∑(x^2) =∑(xy)
Рассчитываем коэффициенты линейного уравнения парной регрессии:
σx^2= (x^2)cp = (xcp)^2
b= (cp(y*x) –cp(y)*cp(x))/(σx^2) (5)
a= cp(y) –b*cp(x)
Таблица 2.2.Линейная регрессия y=a+bx
| n |
y |
x |
yx |
x² |
y² |
y^x |
y-y^x |
| 1 |
68,80 |
45,10 |
3102,88 |
2034,01 |
4733,44 |
61,65 |
7,15 |
| 2 |
61,20 |
59,00 |
3610,80 |
3481,00 |
3745,44 |
56,88 |
4,32 |
| 3 |
59,90 |
57,20 |
3426,28 |
3271,84 |
3588,01 |
57,49 |
2,41 |
| 4 |
56,70 |
61,80 |
3504,06 |
3819,24 |
3214,89 |
55,92 |
0,78 |
| 5 |
55,00 |
58,80 |
3234,00 |
3457,44 |
3025,00 |
56,95 |
-1,95 |
| 6 |
54,30 |
47,20 |
2562,96 |
2227,84 |
2948,49 |
60,93 |
-6,63 |
| 7 |
49,30 |
55,20 |
2721,36 |
3047,04 |
2430,49 |
58,18 |
-8,88 |
| 8 |
61,00 |
55,12 |
3362,32 |
3038,21 |
3721,00 |
58,21 |
2,79 |
| итого |
466,20 |
439,42 |
25524,66 |
24376,62 |
27406,76 |
x |
0 |
| среднее значение |
58,28 |
54,93 |
3190,58 |
3047,08 |
3425,85 |
x |
x |
| σ² |
29,87 |
30,05 |
х |
х |
х |
х |
х |
| σ |
5,47 |
5,48 |
х |
х |
х |
х |
х |
Коэффициенты линейного уравнения парной регрессии можно определить из двух систем уравнений с двумя переменными(4):
8a+439.42b=466.2
439.4a+24376.62 b=25524.66
В результате вычислений получаем значения коэффициентов:
b=-0.34 ,a=77.14
Получено уравнение парной регрессии для описания расходов на покупки товаров от средней зарплаты одного члена семьи
y^=77.14-0.34*x
Это уравнение показывает , что с увеличением среднедневной заработной платы на 1 руб. для расходов на покупку продовольственных товаров снижается на 34 коп.
Надежность полученных результатов оцениваем по ряду коэффициентов (корреляции, детерминации) и критерию Фишера, определяем среднюю ошибку аппроксимации.
Таблица 2.3
| коэффициент корреляции |
коэффициент корреляции показывает , что связь между х и у умеренная, обратная |
| rxy=-0,344 |
rxy=b*(σx/σy) |
| коэффициент детерминации |
вариация результата на 11,9% объясняется ариацией фактора х |
| r²xy=0,119 |
r²=(-0,344)²=0,119 |
-1≤xy≤1 0≤r²xy≤1
|
полученное уравнение регрессии описывает исх. Параметры (х,у) с точностью 11,9%. Влияние прочих факторов оценивается в 88,9% |
| критерий Фишера |
Подставляя в уравнение регрессии фактические значения х, определяем расчетные значения у^х |
| Fфакт. =0,81 Fтабл. =5,99 |
| найдем еличину средней ошибки аппроксимации |
| Fфакт. =(r²/1-r²)*(n-2) |
A=1/n(Ai)=1/n (|y-y^x|/y*100%)=(61,19/8)*100%=7,65% |
| в среднем расчетные значения отклоняются от фактических на 7,65% |
Коэффициент Фишера показывает, что это уравнение не имеет экономического смысла, так как Fфакт.< Fтабл.
Реклама

Полученное значение Fфакт. Указывает на необходимость принять нулевую гипотезу о случайной природу выявленной зависимости и статистической незначимости параметров уравнения и показателей тесноты связи.
Графическое представление полученных результатов показано на рис. 2.1.

Рис.2.1
Из рисунка 2.1. видно, что исходные статистические данные достаточно разборосаны, т.е. явной закономерности не прослеживается.
Результаты вычислений по исходным данным, представлены в таблице 2.1 , полностью совпадают с уже полученным уравнением регрессии.
Таблица 2.4
| -0,34337 |
77,13555 |
| 0,382134 |
21,09393 |
| 0,118608 |
5,924707 |
| 0,807417 |
6 |
| 8,34207 |
210,6129 |
Выводы:
1. Решена задача парной регрессии методом наименьших квадратов.
2. Низкая достоверность результатов объясняется рядом причин:
- собрано малое количество статистических данных, выбраны случайные районы за небольшой отрезок времени;
- в учебных целях добавлены случайные точки, зависящие от порядкового номера студента и числа студентов в группе;
- расходы на покупку продовольственных товаров в общих расходах зависят от ряда факторов: количества членов семьи, иждивенцев, налогов и др., т.е. реально существует более сложная зависимость, чем парная регрессия от ряда экономических факторов.
3. Разобрана учебная задача не имеющая практического приложения.
Задача 3.
На основании исходных данных о реальном ВВП в мире в целом, регионах и странах с 1990 г. По 2000г., представленных в таблице 3.1 провести экономический анализ. Выбрать для сравнения две страны, с помощью ППП получить аналитические зависимости, описывающие ВВП в выбранных стран, по этим уравнениям построить прогноз их развития в 2001-2020 годах, результаты сравнить с официальными опубликованными данными.
Таблица 3.1.Реальный ВВП в странах (млрд.долл. в ППС 1993 г.)
| регионы страны |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
| США |
5971,1 |
5935,5 |
6071,8 |
6260 |
6516,7 |
6725,2 |
6833 |
7024,3 |
7199,9 |
7379,9 |
7564,4 |
| Германия |
1466,5 |
1487 |
1519,7 |
1503 |
1546,6 |
1596,1 |
1648,8 |
1690 |
1732,3 |
1775,6 |
1820 |
| Китай |
1798,5 |
1946 |
2000,9 |
2502,4 |
2802,7 |
3130,6 |
3496,9 |
3846,6 |
4231,2 |
4654,4 |
5119,8 |
| Россия |
993,2 |
943,5 |
804,5 |
735,2 |
656 |
626 |
588 |
600 |
622,1 |
643,9 |
666,4 |
На рис. 3.1 показано графическое изменение ВВП по ряду стран из таблицы 3.1. Их можно сравнивать между собой, определять тенденцию развития. Темпы развития за этот сравнительно небольшой промежуток времени отличаются по странам, вплоть до падения. Так, например, Россия пережила сложный период перехода к рыночной экономике, что привело к уменьшению её ВВП.
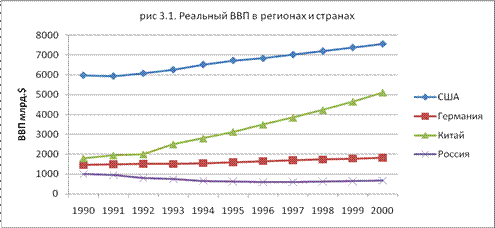
Рис.
Сравнивая темпы роста ВП США и Китая, можно говорить о выравнивании ВВП некотором году при условии их сохранения. По исходным данным табилы3.1, можно построить линейные и логарифмические аппроксимации и графические прогнозы. На рис. 3.2 а.б приведены аппроксимирующие уравнения. Так как достоверность аппроксимации R2 практически одинакова у линейных и логарифмических функций, то аналитический ответ рассчитываем по линейным функциям, приравнивая их и определяя год совпадения ВП :
172,49х-337441=341,03х-677130
(341,03-172,49)х=677130-337441
х=2015,48
Т.е., при сохранении темпов роста в США и Китае ВВП этих стран сравняется к середине 2015 года.
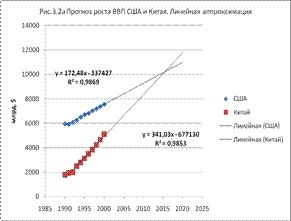
Рис. 1
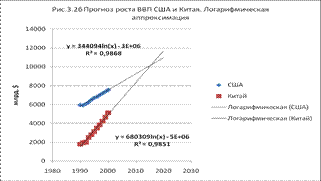
Рис. 2
Выводы
1. Развитие экономических процессов происходит о времени, поэтому многие эконометрические задачи моделируются одномерными временными рядами. Эти задачи имеют большое преимущество – они двумерные, т.е. моделируются на плоскости и исходные статистические данные можно представить графически.
2. Результаты получаются с помощью ППП и по коэффициенту аппроксимации R² выбирается наиболее достоверная аналитическая зависимость.
3. Эконометрическое моделирование временных рядов позволяет анализировать имеющиеся статистические данные в различных областях человеческой деятельности – от ВВП до добычи нефти по странам и регионам. В ряде случаев возможно составлять прогнозы на будущее, изучать динамику экономических процессов в микро- и макропроцессах.
|