Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Московский государственный гуманитарный университет
им. М.А. Шолохова
Егорьевский филиал
Кафедра экономики и управления.
Курсовая работа по математике
Тема:
«Многомерная геометрия».
Студентки II курса Очного отделения
факультета информатики и математики
группы 21
Волковой Марии Вячеславовны
Работу проверила
Научный руководитель
Бармакова Татьяна Владимировна
Егорьевск 2008
Оглавление:
Введение
…………………………………………………………………3
Глава
I
.
Пространства с квадратичной метрикой……….……………………..5
1.1.
Скалярное произведение……………………………………………..5
1.2.
Норма вектора…………………………………………………………8
1.3.
Ортонормированные базисы……………………………………….11
1.4.
Ортогональная проекция. Ортогонализация……………………...13
Глава
II
. Аффинные преобразования
……………………………………….20
2.1.
Аффинные преобразования на плоскости…………………...….20
2.2.
Однородные координаты точки…………………………………….23
2.3.
Аффинные преобразования в пространстве………………………..32
2.4.
Формула обратного преобразования………………………………41
2.5.
Основнаятеорема теории аффинных преобразований…………...42
Глава
III
.
Частные виды аффинных преобразований в сопряжённых комплексных координатах…………………………………………………….43
3.1.
Преобразование подобия……………………………………….......43
3.2.
Преобразование родства……………………………………………45
3.2.1.
Понятие преобразования родства……………………………45
3.2.2.
Сжатие и его частные виды………………………………….47
Список литературы…………………………………………………...49
Введение
В математике и в ее приложениях часто приходиться рассматривать некоторые множества объектов, для которых установлены так называемые линейные операции: сложение и умножение на число. Например, в механике рассматривают также сложение скоростей и умножение скорости на число; рассматривают сложение ускорений и умножение ускорения на число. Силы, скорости и ускорения различны по своей физической природе. Однако линейные операции, которые производятся над ними, единообразны с геометрической точки зрения. Рассмотрим, например, множество всех функций, непрерывных на числовой оси, или множество всех периодических функций с данным периодом, или множество всех алгебраических многочленов. В каждом из этих множеств мы можем естественным образом рассматривать линейные операции. Объекты, о которых мы сейчас говорим, не похожи на силы, скорости и ускорения или на геометрические векторы. Линейные операции над ними также не похожи на линейные операции над векторными величинами механики или над геометрическими векторами.
Реклама

Линейное пространство не будет содержать каких-либо описаний элементов рассматриваемых множеств или производимых линейных операций, общие для всех частных случаев. Эти требования выражаются аксиомами линейного пространства. Следует заметить, что требования, которые выражены в аксиомах, весьма немногочисленны, и остается возможность добавлять к ним новые предположения. Поэтому в общем понятии линейного пространства возникает некоторая классификация, так что все-таки приходится иметь дело не с единым линейным пространством, а с различными классами линейных пространств, и теория, основанная на аксиомах линейного пространства, разветвляется.
Прежде всего, все линейные пространства разделяются на конечномерные и бесконечномерные. К числу конечномерных пространств принадлежит трехмерное пространство геометрических векторов. Это пространство содержит в себе бесконечно много двумерных и одномерных пространств, называемых подпространствами. Таким образом. Для одномерных, двумерных и трехмерных линейных пространств мы имеем геометрические модели, с которыми естественно связаны наши наглядные представления о векторах. При переходе к многомерным пространствам наглядность частично теряется, но теория этих пространств сохраняет геометрический характер. Вместе с тем линейные пространства называют также векторными пространствами. Геометричность терминологии и основных понятий линейной алгебры помогает ее контактам с геометрией.
Мы имеем в виду здесь аналитическую геометрию, причем многомерную, т.е. многомерный аналог обычной (трехмерной) аналитической геометрии. Более того, линейная алгебра и аналитическая геометрия настолько тесно связаны, что между ними трудно провести четкую грань. И не будем к этому стремиться. Можно сказать, что предметом линейной алгебры является многомерная аналитическая геометрия.
Глава I. Пространства с квадратичной метрикой
1.1. Скалярное произведение
1.
Пусть L
– действительное линейное пространство. Введем
в пространстве L
новую операцию – скалярное умножение векторов.
Действие скалярного умножения ставит в соответствие каждой паре векторов x
, y
изL
действительное число, которое обозначается (x
, y
) и называется скалярным
произведением
вектора x
на вектор y
.
Реклама

По аналогии с элементарной аналитической геометрией потребуем соблюдения следующих свойств:
1) Коммутативность: (x
,y
) = (x
, y
).
2) Распределительность (дистрибутивность): (x
1
+ x
2
, y
) = (x
1
,y
) +
+ (x
2,
y
).
3) Однородность: (
ax
,
y
)=а (
x
,
y
)
для любого действительного числа а
.
4) Невыдержанность: если (x
,
y
) = 0 при фиксированном x
и любому y
изL
, то x
= 0.
Здесь всюду x
,
y
,
x
1
,
x
2
– произвольные векторы пространства L
.
2.
Обратим внимание на то, что в элементарной аналитической геометрии перечисленные выше свойства скалярного произведения доказываются как теоремы, а здесь мы рассматриваем эти свойства как аксиомы, включая их в определение скалярного произведения.
3.
Второе и третье свойства вместе означают линейность скалярного произведения по первому аргументу.
Итак скалярное произведение(
x
,
y
) представляют собой билинейную форму, симметричную
согласно первому свойству и невырожденную
вследствие четвертого свойства. Действительно, четвертое свойство означает, что нулевое подпространство билинейной формы (x
,
y
) нульмерно, откуда и вытекает ее невырожденность.
4.
Очевидно, справедливо и обратное утверждение:
Каждую невырожденную симметричную билинейную форму
g
(
x
,
y
), заданную в пространстве
L
, можно принять в качестве скалярного произведения, положив
(
x
,
y
) =
g
(
x
,
y
)
Для любых
x
,
y
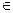 L
.
L
.
Замечание.
Разумеется скалярное произведение зависит от выбора формы g
(
x
,
y
)
. Если в качестве скалярного произведения выбирать разные формы, то для данной пары векторов x
,
y
пространстваL
скалярное произведение будет получать, разные численные значения.
5.
Пусть в пространстве L
введено скалярное произведение (
x
,
y
) =
=
g
(
x
,
y
).
Предполагая пространство n
– мерным, возьмем в нем произвольный базис e
1
,
. . . ,en
.
Если x
=
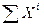 e
I
,
y
= e
I
,
y
= 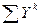 e
k
,
то скалярное произведение запишется в координатах так:
e
k
,
то скалярное произведение запишется в координатах так:
(
x
,
y
) =
g
(
x
,
y
) =
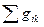 xi
y k
. (1) xi
y k
. (1)
где g
I
k
–коэффициенты билинейной формы g
(
x
,
y
)
в данном базисеe
1
…,en
. Они являются значениями этой формы на базисных векторах, то есть их скалярным произведением.
Таким образом,
(
e I
,
e k
) =
g I k
. (2)
Причем g
I
k
=
g
k
i
. Равенства (2) составляют таблицу умножения базисных векторов.
Если правые части таблицы (2) даны, то тем самым однозначно определено скалярное произведение любой пары векторов x
, у
согласно равенству (1).
6.
Определение 1.
Векторы x
, у
называются ортогональными
, если
(x,
у
) = 0.
В координатах условие ортогональности векторов x
, у
имеет вид
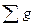 I
k
xi
xk
= 0. I
k
xi
xk
= 0.
Определение 2.
Вектор x
ортогонален подпространству  , если
, если
(
x
, у)
= 0 для любого у 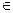  .
.
Заметим, что если  имеет размерность k
, то для ортогональности вектора x
подпространству
имеет размерность k
, то для ортогональности вектора x
подпространству  достаточно, чтобы x
был ортогонален к каким – нибудь независимым векторам в числе k
, лежащим в
достаточно, чтобы x
был ортогонален к каким – нибудь независимым векторам в числе k
, лежащим в  . В самом деле, если независимые вектора а1
,…,
а
k
лежат в
. В самом деле, если независимые вектора а1
,…,
а
k
лежат в  и если (
x
,
a
1
) = 0
,…,(
x
,
a
k
) = 0,
то для любого y
и если (
x
,
a
1
) = 0
,…,(
x
,
a
k
) = 0,
то для любого y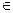 L
имеем y
=
L
имеем y
= 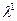 a
1
+
…+
a
1
+
…+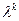 a
k
, откуда
a
k
, откуда
(
x
,
y
) =
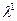 (
x
,
a
1
) +
…+
(
x
,
a
1
) +
…+
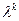 (
x
,
a
k
) = 0
.
(
x
,
a
k
) = 0
.
Определение 3.
Подпространства  , , 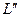 называются ортогональными
, если (
x
, у)
= 0 для любого x
называются ортогональными
, если (
x
, у)
= 0 для любого x
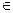  и любого у
и любого у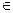 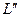 .
.
Определение 4.
Подпространство 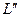 называется ортогональным дополнением
подпространства
называется ортогональным дополнением
подпространства  в пространстве L
, если
в пространстве L
, если и
и 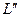 ортогональны и их прямая сумма совпадает сL
.
ортогональны и их прямая сумма совпадает сL
.
Замечание.
Подчеркнем, что ортогональность векторов и ортогональность подпространств существенно зависит от того, какая именно билинейная форма g
(
x
,
y
)
взята в качестве скалярного произведения (
x
,
y
)
в пространствеL
.
1.2. Норма вектора
1.
Пусть в линейном пространстве L
задано скалярное произведение
Определение.
Нормой вектора
x
называется число
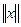 = + = + 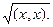 (1) (1)
Норма является обобщением понятия модуля или длины вектора, известного из элементарной геометрии.
Скалярное произведение (
x
,
x
)
является действительным числом, но оно может не быть положительным, так что норма вектора может оказаться мнимой. Условимся считать, что радикал в формуле (1) может быть либо неотрицательным действительным числом, либо мнимым числом с положительным множителем при l
(
l
= +
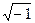 )
.
)
.
2.
Из определения нормы следует, что
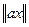 = = 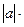 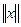 . .
для любого x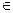 L
и любого числа a
. L
и любого числа a
.
В частности,
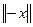 = =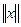 , , 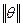 = 0. (2) = 0. (2)
Нулевые векторы, норма которых равна нулю, называются изотропными
. Изотропные векторы существуют тогда и только тогда, когда квадратичная форма (
x
,
x
)
не является знакоопределенной.
3.
Квадратичная форма 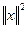 = (
x
,
x
)
называется метрической формой рассматриваемого пространства. = (
x
,
x
)
называется метрической формой рассматриваемого пространства.
Она определяется в билинейной форме (
x
,
y
)
и в свою очередь определяет ее как свою полярную форму. Таким образом, задание скалярного произведения и задание квадратичной формы для измерения норм векторов равносильны. Поэтому пространства с заданным скалярным произведением называют также пространствами с квадратичной метрикой.
Если пространство n
– мерно, то метрическая форма в координатах имеет вид
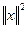 = (
x
,
x
) = = (
x
,
x
) =
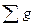 i
k
x
i
x
k
. i
k
x
i
x
k
.

4. Теорема.
Если метрическая форма является положительно отдельной, то для любых двух векторов
x
,
y
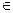 L
соблюдается неравенство
L
соблюдается неравенство
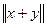 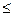 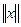 + + 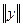 .
(3) .
(3)
Доказательство.
Используем неравенство Коши – Буняковского
(x
,
x
)2
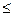 (
x
,
x
) ∙(
y
,
y
).
(4)
(
x
,
x
) ∙(
y
,
y
).
(4)
Учитывая (4), находим, что
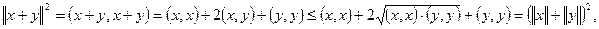
отсюда следует (3).
Замечание.
Из (3) следует, что если метрическая форма положительно определена, то
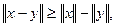 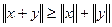 . .
5.
Рассмотрим аффинное пространство F
,
к которому соответствует линейное пространствоL
с квадратичной метрикой.
Для каждой пары точек A
,
B
изF
определим расстояние 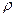 (
A
,
B
),
пологая его равным норме вектора (
A
,
B
),
пологая его равным норме вектора 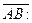
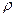 (A, B) = (A, B) =
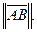 (5)
(5)
Имеем
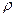 (
A
,
B
) = (
A
,
B
) = 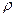 (
B
,
A
),
(
B
,
A
),
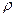 (
A
,
A
)= 0.
(6) (
A
,
A
)= 0.
(6)
Формула (6) следует из (2) и (5).
6.
В случае положительно определенной метрической формы (
x
,
x
)
расстояние между точками равно нулю только тогда, когда точки совпадают, и, кроме того, для любых трех точек A
,
B
,
C
из F
соблюдается неравенствотреугольника
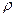 (
A
,
C
) (
A
,
C
)
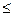
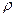 (
A
,
B
),
(
A
,
B
),
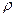 (
B
,
C
).
(7) (
B
,
C
).
(7)
Неравенство (7) следует из неравенства (3) и формулы (5).
7.
Если между точками аффинного пространства F
определено расстояние по формуле (5), то говорят, что в аффинном пространстве F
задана квадратичная метрика. В аффинных координатах квадрат расстояния имеет выражение
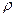 2
(A, B) = 2
(A, B) =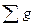 i k
(x i
2
– x i
1
)(x k
2
– x k
1
),
(8) i k
(x i
2
– x i
1
)(x k
2
– x k
1
),
(8)
где x
i
1
,…x
n
1
– аффинные координаты точки A
,
x
i
2
,…,x
n
2
–
аффинные координаты точки B.
Правую часть (8), квадратичную относительно разностей координат произвольных точек A
и B
, называют метрической формой пространства F
.
1.3.Ортонормированные базисы
1. В пространстве с квадратичной метрикой базисы не равноправны. Среди них есть такие, которые наиболее удобны с точки зрения данной метрики.
Именно, базис e
1
,…,en
можно выбрать так, чтобы метрическая форма g
(
x
,
x
)
имела в нем нормальный вид
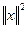 = g (x, x) = (x1
)2
+ …+ (x k
)2
- (x k +1
) 2
- … - (x n
)2
. = g (x, x) = (x1
)2
+ …+ (x k
)2
- (x k +1
) 2
- … - (x n
)2
.
Тогда скалярное произведение двух векторов представится так:
x y = x 1
y1
+ … + x k
y k
– x k
+ 1
y k + 1
- … - x n
y n
.
Ясно, что скалярное произведение (
e
I
,
e
j
) = 0
, если i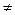 j
, то есть при i j
, то есть при i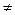 j
, j
,
то есть при i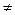 j
базисные векторы ортогональны. При этом j
базисные векторы ортогональны. При этом  = 1, если = 1, если
i
= 1,…,
k
;
 = - 1,
если i
=
k
+ 1,…,
n
.
Тем самым векторы базиса нормированы так, что квадраты их норм по модулю равны единице. Векторы e
i
называются единичными, если i
= - 1,
если i
=
k
+ 1,…,
n
.
Тем самым векторы базиса нормированы так, что квадраты их норм по модулю равны единице. Векторы e
i
называются единичными, если i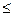 k
, мнимоединичным, если i
k
, мнимоединичным, если i
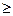 k
+ 1.
Вообще вектор a
называется единичным, если
k
+ 1.
Вообще вектор a
называется единичным, если 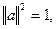 мнимоединичным, если мнимоединичным, если 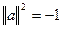 . .
Определение.
Базис e
1
,…,
en
,
удовлетворяющий перечисленным в этом пункте условиям, называется ортонормированным.
Теорема 1.
В
n
– мерном линейном пространстве с заданной квадратичной метрикой всякий набор из попарно ортогональных единичных или мнимоединичных векторов общим числом
n
является базисом, в котором метрическая форма имеет нормальный вид.
Доказательство.
Пусть e
1
,…,
en
– указанный набор векторов. Убедимся, что они линейно независимы. Рассмотрим соотношение
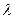 1
e
1
+ 1
e
1
+
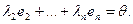
Отсюда, умножая скалярно наe
1
,
получим
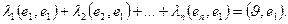
Но по условию (
e
1
,
e
1
) = 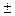 1, (
e
j
,
e
1
) = 0 (
j 1, (
e
j
,
e
1
) = 0 (
j
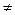 1);
кроме того, (
1);
кроме того, (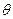 ,
e
1
) = 0
. Следовательно, ,
e
1
) = 0
. Следовательно, 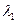 = 0.
Аналогично докажем, что векторы e
1
,…,
en
независимы и, значит, действительно составляют базис. = 0.
Аналогично докажем, что векторы e
1
,…,
en
независимы и, значит, действительно составляют базис.
Так как g
(
e
i
,
e
i
) = (
e
i
,
e
i
) =
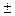 1
g
(
e
i
,
e
i
)= (
e
i
,
e
i
)=0,
то форма g
(
e
i
,
e
i
)
в базисе e
1
,…,
en
имеет нормальный вид.
1
g
(
e
i
,
e
i
)= (
e
i
,
e
i
)=0,
то форма g
(
e
i
,
e
i
)
в базисе e
1
,…,
en
имеет нормальный вид.
2.
Наряду с доказанной выше теоремой 1 мы отметим следующее утверждение.
В n
– мерном линейном пространстве всегда можно задать, причем единственным способом, такую квадратичную метрику, что произвольный заранее данный базис e
1
,…,
e
k
,
e
k
+ 1,…,
en
станет ортонормированным, его векторы e
1
,…,
e
k
станут единичными, а векторы e
k
+ 1,…,
en
– мнимо- единичными; здесь k
– также любое заранее данное целое число от 0 доn
.
Доказательство.
Искомая метрика однозначно определяется заданием метрической формы g
(
x
,
x
)
которая в базисе e
1
,…,
e
k
,
e
k
+ 1,…,
en
имеет вид
g(x, x) = (x1
)2
+…+(x k
)2
– (x k+ 1
)2
- …- (x n
)2
.
3.
Согласно закону инерции квадратичных форм число единичных и число мнимо-единичных векторов не зависит от выбора базиса, ортонормированного в данной квадратичной метрике.
Определение.
Числи k
единичных векторов ортонормированного базиса называется положительным индексом
пространства с данной квадратичной метрикой.
Если k
=
n
или еслиk
= 0,
то пространство называется евклидовым
.
Если 1
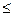 k
k
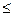 n
– 1
, то пространство называется псевдоевклидовым
.
n
– 1
, то пространство называется псевдоевклидовым
.
Особенно большое значение имеет псевдоевклидово пространство при
k
=
n
– 1
. Оно называется пространством Минковского и при n
= 4
играет важную роль в теории относительности.
1.4.Ортогональная проекция. Ортогонализация
1. В этом параграфе рас смотрим евклидово пространство L, то есть линейное пространство со знакоопределенной метрической формой. смотрим евклидово пространство L, то есть линейное пространство со знакоопределенной метрической формой.
Будем считать метрическую форму положительно определенной.
Размерность пространства L
может быть бесконечной.
Пусть в L
дано подпространство  . Допустим, что вектор x . Допустим, что вектор x
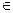 L
представляется в виде суммы
L
представляется в виде суммы
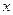 = =
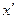 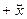
 (1) (1)
где 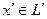 , а , а 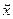 ортогонален к ортогонален к  . Тогда вектор . Тогда вектор 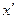 называется ортогональной
проекцией
вектора x
на подпространство называется ортогональной
проекцией
вектора x
на подпространство . Ортогональная проекция вектора x
на . Ортогональная проекция вектора x
на  единственна. В самом деле пусть имеется другое разложение единственна. В самом деле пусть имеется другое разложение 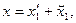 где где 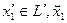 ортогонален к ортогонален к  . В этом случае . В этом случае 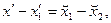 отсюда отсюда 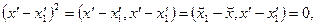 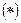 так как так как 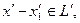 а а 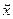 и и 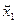 ортогональны к ортогональны к  . Из . Из 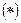 следует, что следует, что 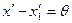 то есть то есть 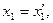 поскольку метрическая форма пространства положительно определена. поскольку метрическая форма пространства положительно определена.
Частный случай.
Когда L
трехмерно  двумерно, показан на рис. 1. двумерно, показан на рис. 1.
Преобразование пространства L
,
которое каждому вектору x
ставит в соответствии вектор 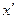 согласно формуле (1), тоже называется ортогональной проекцией на согласно формуле (1), тоже называется ортогональной проекцией на  . .
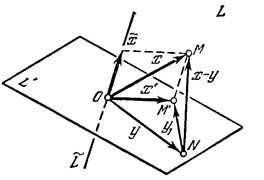 Если пространство L
рассматривается как точечное, то а Если пространство L
рассматривается как точечное, то а  - как плоскость в нем, то точка - как плоскость в нем, то точка 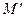 с радиус – вектором с радиус – вектором 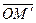 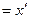 называется ортогональной проекцией на L
точки M
на называется ортогональной проекцией на L
точки M
на  представляет собой представляет собой
ближайшую к M
точку в  . Пусть . Пусть 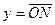 - произвольный вектор подпространства - произвольный вектор подпространства  . .
Нужно доказать, что 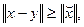 (2) (2)
причем равенство в (2) достигается только тогда, когда 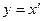 (то есть когда N
совпадает с (то есть когда N
совпадает с 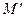 , рис.1) , рис.1)
Причем 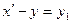 . Тогда . Тогда 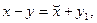 и и 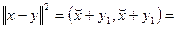
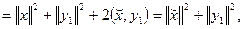 (3) (3)
поскольку 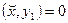 вследствие ортогональности вектора вследствие ортогональности вектора 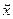 подпространству подпространству
 , содержащему , содержащему  . .
Заметим, что 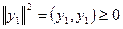 ввиду положительной определенности метрической формы рассматриваемого пространства. Поэтому (2) следует из (3). Равенство в (2) достигается лишь тогда, когда ввиду положительной определенности метрической формы рассматриваемого пространства. Поэтому (2) следует из (3). Равенство в (2) достигается лишь тогда, когда 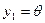 ( то есть когда ( то есть когда 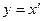 ). ).
3.
Пусть
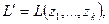
где 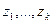 - некоторая конечная независимая система векторов из L
.
В этом случае для нахождения ортогональной проекции - некоторая конечная независимая система векторов из L
.
В этом случае для нахождения ортогональной проекции 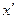 заданного вектора x
на подпространство заданного вектора x
на подпространство  достаточно надлежащим образом вычислить коэффициенты достаточно надлежащим образом вычислить коэффициенты 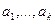 в разложении в разложении
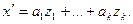 (4) (4)
С этой целью запишем условие ортогональности вектора 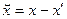 к каждому из векторов z
j к каждому из векторов z
j
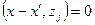 (5)
(5)
Подставив разложение (4) в (5) и используя свойства скалярного произведения, получаем для 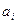 систему линейных уравнений систему линейных уравнений
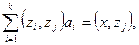 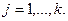 (6) (6)
Определить системы (6) представляет собой определитель Грамма для положительно определенной квадратичной формы (
x
,
x
)
и независимых векторов 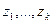 . Поэтому он положителен, а система (6) однозначно разрешима. Тем самым искомая проекция найдется. . Поэтому он положителен, а система (6) однозначно разрешима. Тем самым искомая проекция найдется.
4.
Ниже нам потребуется следующая
Лемма. Пусть в пространстве с положительно определенной метрической формой имеется система попарно ортогональных векторов
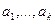 , то есть (
a
i
,
a
k
)= 0 при
i
=
k
. Если ни один из этих векторов не нулевой, то они линейно независимы. , то есть (
a
i
,
a
k
)= 0 при
i
=
k
. Если ни один из этих векторов не нулевой, то они линейно независимы.
Доказательство.
Рассмотрим соотношение
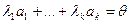 (7) (7)
Умножим (7) скалярно на a
1
:
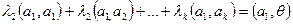 (8)
(8)
Так как 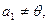 а метрическая форма положительно определена, то а метрическая форма положительно определена, то 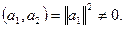 Остальные скалярные произведения в левой части (8) обратятся в нуль по условию леммы; Остальные скалярные произведения в левой части (8) обратятся в нуль по условию леммы; 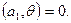 Аналогично устанавливается, что Аналогично устанавливается, что 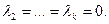 Лемма доказана. Лемма доказана.
5.
Пусть в пространстве L дана упорядоченная система линейно независимых векторов 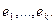 Речь будет идти о замене этой системы другой системой векторов, ортогональной и в некотором смысле эквивалентной данной. С этой целью проводится геометрическое построение, называемое процессом ортогонализации. Оно напоминает процесс выбора базиса при приведении квадратичной формы к каноническому виду методом Якоби. Речь будет идти о замене этой системы другой системой векторов, ортогональной и в некотором смысле эквивалентной данной. С этой целью проводится геометрическое построение, называемое процессом ортогонализации. Оно напоминает процесс выбора базиса при приведении квадратичной формы к каноническому виду методом Якоби.
Новая система векторов 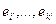 Строится с соблюдением следующих условий: Строится с соблюдением следующих условий:
1)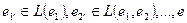 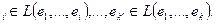
2) Векторы 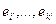 попарно ортогональны. попарно ортогональны.
3) Система 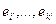 линейно независима. линейно независима.
В таком случае говорят, что система векторов получена из первоначальной системы 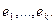 процессом ортогонализации. процессом ортогонализации.
Если данная система состоит из трех векторов e1
, e2
, e3
в трехмерном евклидовом пространстве, то новую систему 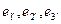 построим так: построим так:
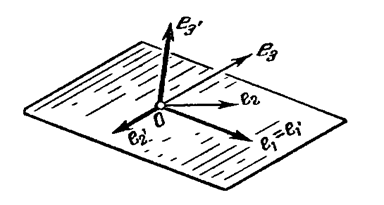 первый вектор сохраним 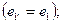
второй вектор проведем к нему ортогонально в плоскости, проходящей через e
1
и e
2
;
третий вектор проведем ортогонально этой плоскости (рис 1).
Переходя к случаю большой размерности, нужно четвертый вектор располагать перпендикулярно данному трехмерному пространству и т. д. В общем случае положим:
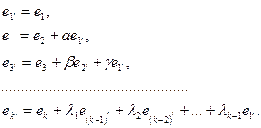 (9) (9)
Из формул (9) следует, что векторы 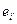 расположены в нужных линейных оболочках и являются ненулевыми вследствие независимости векторов расположены в нужных линейных оболочках и являются ненулевыми вследствие независимости векторов 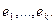
Остается подобрать коэффициенты 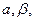 … так, чтобы векторы … так, чтобы векторы 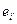 были попарно ортогональны. Тогда система были попарно ортогональны. Тогда система 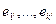 будет независимой по лемме. будет независимой по лемме.
Найдем a
. Мы имеем
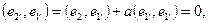
отсюда
a
= -
 (10)
(10)
деление выполнимо, так как 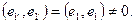 Вектор Вектор 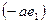 (рис. 3). (рис. 3).
Дальше обеспечим ортогональность третьего вектора первым двум:
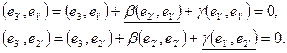
Подчеркнутые члены обращаются в нуль, а 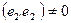 по построению. Поэтому находим по построению. Поэтому находим
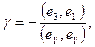 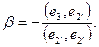 (11) (11)
Формулы (9) и (11) геометрически означают, что для построения вектора 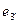 нужно из вектора нужно из вектора 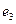 вычесть его ортогональную проекцию на подпространство вычесть его ортогональную проекцию на подпространство 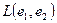 (рис. 4) (рис. 4)
Дальше процесс идет аналогично.

6.
В процессе ортогонализации иногда бывает важно обеспечить соблюдение еще двух дополнительных условий.
4) При любом 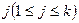 система система 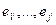 ориентирована так же, как система ориентирована так же, как система 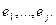
5) 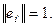
Формулы (9) гарантируют соблюдение условия 4). В самом деле, из (9) имеем
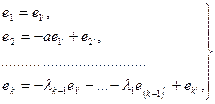
Так, что в матрице, выражающей 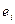 через через 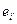 , левый верхний минор порядкаj
(при любом , левый верхний минор порядкаj
(при любом 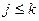 ) положителен (равен + 1). ) положителен (равен + 1).
Для того чтобы обеспечить условие 5), достаточно после проведения ортогонализации каждый из полученных векторов разделить на его норму.
Замечание.
Нетрудно доказать (например по индукции), что условия 1) – 5) по данной системе 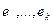 однозначно определяют систему векторов однозначно определяют систему векторов 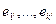 . .
7.
Многочлены Лежандра.
В математическом анализе и его приложениях приходится использовать разложение произвольных функций в ряды по данным функциям, рассматривая такие разложения функций аналогично разложениям векторов по данному базису. При этом удобно иметь аналоги ортогонального базиса; таковыми являются ортогональные системы функций. Одним из простейших примеров ортогональных систем являются многочлены Лежандра.
В пространстве непрерывных функций на отрезке 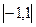 вводится квадратичная метрика со скалярным произведением вводится квадратичная метрика со скалярным произведением
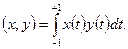 (12) (12)
Соответственно
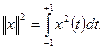 (13) (13)
Следует определить внимание на ее положительную определенность: 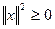 , причем , причем 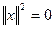 тогда и только тогда, когда непрерывная функция тогда и только тогда, когда непрерывная функция 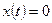 во всех точках отрезка. во всех точках отрезка.
Возьмем систему одночленов
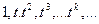 (14) (14)
и причем к ней процесс ортогонализации. В результате получим последовательность многочленов
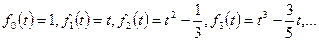 (15) (15)
Номера многочленов (15) выбраны так, чтобы они совпадали с их степенями. Коэффициенты многочленов вычисляются согласно формулам (9) с учетом (10), (11), (12) и (14).
После специальной нормировки вида
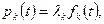
где 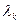 выбираются из условия выбираются из условия
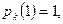 (16) (16)
Получаем последовательность многочленов 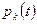 называемых многочленами Лежандра. Можно доказать, что называемых многочленами Лежандра. Можно доказать, что
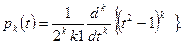 (17) (17)
Учитывая замечание в п. 6, для этого достаточно проверить, что все многочлены (17) попарно ортогональны и что они удовлетворяют условию (16).
Можно доказать также, что
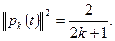
Таким образом, система многочленов Лежандра ортогональна, но не нормирована.
Глава
II.
Аффинные преобразования
2.1
. Аффинные преобразования на плоскости
В компьютерной графике все, что относится к двумерному случаю принято обозначать символом (2D) (2-dimention).
Допустим, что на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 5). Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел – (x*
, y*
).

 
Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:
x*
=ax+ by +l, (2.1)
y*
=gx+ by + m, (2.2)
где a, b, g, l, m -- произвольные числа, связанные неравенством:
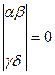 (2.3) (2.3)
Формулы (2.1) и (2.2) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 6) – в этом случае произвольная точка М остается той же, изменяются лишь ее координаты (х, у) | (х*
, y*
), либо изменяется точка и сохраняется координатная система (рис. 7) – в этом случае формулы (2.1) и (2.2) задают отображение, переводящее произвольную точку М (х, у) в точку М* (х*, у*), координаты которой определены в той же координатной системе.
X*
 

  Y* Y*

 
В дальнейшем, формулы (2.1) и (2.2) будут рассматриваться как правило, согласно которому в заданной системе прямолинейных координат преобразуются точки плоскости.
В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики. При исследовании геометрического смысла числовых коэффициентов в формулах (2.1) и (2.2) для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой.
1.
Поворот вокруг начальной точки на угол j (рис. 8) описывается формулами:
х* = xcosj - ysinj, (2.3)
y* = xsinj - ycosj. (2.4)
2.
Растяжение (сжатие) вдоль координатных осей можно задать так:
x* = ax, (2.5)
y* = dy, (2.6)
a > 0, d > 0. (2.7)
Растяжение (сжатие) вдоль оси абсцисс обеспечивается при условии, что a > 1 (a < 1). На рис. 5 a = d > 1.
2.
Отражение (относительно оси абсцисс) (рис. 10) задается при помощи формул:
x* = x, (2.8)
y* = -y. (2.9)
3.
На рис. 11 вектор переноса ММ* имеет координаты l, m. Перенособеспечиваетсоотношения:
x* = x + l, (2.10)
y* = y + m. (2.11)
 
 
  
  
 
 
Выбор этих четырех частных случаев определяется двумя обстоятельствами.
1.
Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы).
2.
Как известно из курса аналитической геометрии, любое преобразование вида (2.1) всегда можно представить как последовательное исполнение (суперпозицию) простейших преобразований вида 1 – 4 (или части этих преобразований).
Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (2.1) можно описать при помощи отображений, задаваемых формулами (2.3) – (2.11).
Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям 1 – 3, строятся легко и имеют соответственно следующий вид:
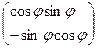 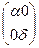 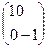
2.2. Однородные координаты точки
Пусть М – произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел х1
, х2
, х3
, связанных с заданными числами х и у следующими соотношениями:
x1
/ x3
= x, x2
/ x3
= y (3.1)
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М (х, у) плоскости ставится в соответствие точка МЭ
(х, у, 1) в пространстве.
Необходимо заметить, что произвольная точка на прямой, соединяющей начало координат, точку О (0, 0, 0), с точкой МЭ
(х, у, 1),может быть задана тройкой чисел вида (hx, hy, h).
Будем считать, что h = 0. Вектор с координатами hx, hy, h является направляющим вектором прямой, соединяющей точки О (0, 0, 0) и МЭ
(х, у, 1). Эта прямая пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху.
Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (hx, hy, h), h = 0, устанавливается взаимно однозначное соответствие, позволяющее считать числа hx, hy, h новыми координатами этой точки.
Широко используемые в проективной геометрии однородные координаты позволяют эффективно описывать так называемые несобственные элементы (по существу, те, которыми проектная плоскость отличается от привычной евклидовой плоскости).
В проективной геометрии для однородных координат принято следующее обозначение:
х : у : 1 (3.2)
или, более общо,
х1
: х2
: х3
(3.3)
(здесь непременно требуется, чтобы числа х1
, х2
, х3
одновременно в нуль не обращались).
Применение однородных координат оказывается удобным уже при решении простейших задач.
Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения h (например, h = 1) точку с однородными координатами (0.5, 0.1, 2.5) представить нельзя. Однако при разумном выборе h можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при h = 10 для рассматриваемого примера имеем (5, 1, 25).
Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению для точки с координатами (80000, 40000, 1000) можно взять, например, h = 0.001. В результате получим (80, 40, 1).
Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.
Считая, h = 1, сравним две записи:
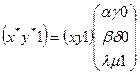 (3.4) (3.4)
Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим формулы (2.1) и (2.2) и верное числовое равенство 1 = 1. Тем самым сравниваемые записи можно считать равносильными.
Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, то есть найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью поставленной задачи и с описанными выше частными случаями разбивают на несколько этапов.
На каждом этапе пишется матрица, соответствующая тому или иному из выделенных выше случаев 1 – 4, обладающих хорошо выраженными геометрическими свойствами.
Выпишем соответствующие матрицы третьего порядка.
А. Матрица вращения (rotation)
cosj sinj 0
[R] = -sinj cosj 0 (3.5)
0 0 1
Б. Матрица растяжения-сжатия (dilatation)
a 0 0
[ D] = 0 d 0 (3.6)
0 0 1
В. Матрица отражения (reflection)
1 0 0
[M] = 0 -1 0 (3.7)
0 0 1
Г. Матрица переноса (translation)
1 0 0
[T] = 0 1 0 (3.8)
l m 1
Рассмотрим примеры аффинных преобразований плоскости.
Пример 1.
Построить матрицу поворота вокруг точки А (a, b) на угол j (рис. 12).
  j j
1-й шаг.
Перенос на вектор – А (-a, -b) для смещения центра поворота с началом координат;
1 0 0
[T-
A
] = 0 1 0 (3.9)
-a -b 1
матрица соответствующего преобразования.
2-й шаг.
Поворот на угол j;
 cosj sinj 0 cosj sinj 0
[Rj
] = -sinj cosj 0 (3.10)
0 0 1
матрица соответствующего преобразования.
3-й шаг.
Перенос на вектор А (a, b) для возвращения центра поворота в прежнее положение;
1 0 0
[TA
] = 0 1 0 (3.11)
ab 1
матрица соответствующего преобразования.
Перемножим матрицы в том же порядке, как они выписаны:
[ T-
A
] [ Rj
] [ TA
].
В результате получим, что искомое преобразование (в матричной записи) будет выглядеть следующим образом:
cosjsinj 0
(x* y* 1) = (xy1) -sinj cosj 0 (3.12)
-a cos j + b sin j + a -a sin j - b cos j + b 1
Элементы полученной матрицы (особенно в последней строке) не так легко запомнить. В то же время каждая из трех перемножаемых матриц по геометрическому описанию соответствующего отображения легко строится.
Пример 2.
Построить матрицу растяжения с коэффицентами растяжения a вдоль оси абсцисс и b вдоль оси ординат и с центром в точке А (a, b).
1-й шаг.
Перенос на вектор –А (-a, -b) для совмещения центра растяжения с началом координат;
1 0 0
[T-
A
] = 0 1 0 (3.13)
-a -b 1
матрица соответствующего преобразования.
2-й шаг.
Растяжение вдоль координатных осей с коэффицентами a и b соответственно; матрица преобразования имеет вид
a 0 0
[ D] = 0 d 0 (3.14)
0 0 1
3-й шаг.
Перенос на вектор А (a, b) для возвращения центра растяжения в прежнее положение; матрица соответствующего преобразования:
1 0 0
[TA
] = 0 1 0 (3.15)
ab 1
Премножив матрицы в том же порядке
[ T-
A
] [ D ] [ TA
],
получим окончательно
a 0 0
( x* y* 1) = (xy1) 0 d 0 (3.16)
(1 - a)a (1 - d)b 1
Рассуждая подобным образом, то есть разбивая предложенное преобразование на этапы, поддерживаемые матрицами [ R ], [ D ], [ M ], [ T ], можно построить матрицу любого аффинного преобразования по его геометрическому описанию.
2.3.
Аффинные преобразования в пространстве
Рассмотрим трехмерный случай (3D) (3-dimension) и сразу введем однородные координаты.
Поступая аналогично тому, как это было сделано в размерности два, заменим координатную тройку (x, y, z), задающую точку в пространстве, на четверку чисел
(xyz 1)
или, более общо, на четверку
(hxhyhz), h = 0.
Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно не равных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя.
Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.
Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Поэтому вполне уместно сначала подробно описать матрицы именно этих преобразований (ясно, что в данном случае порядок матриц должен быть равен четырем).
А.
Матрицы вращения в пространстве.
Матрица вращения вокруг оси абсцисс на угол j:
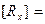
 1 0 0 0 1 0 0 0
0
cos j sin j 0 0 -sin j cos j 0
0 0 0 1
Матрица вращения вокруг оси ординат на угол y:
 cosy 0 -siny 0 cosy 0 -siny 0
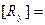
0 1 0 1 siny 0cosy 0
0 0 0 1
Матрица вращения вокруг оси аппликат на угол c:
cos c sin c 0 0
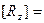 -sin -sin
c cos c 0 00 0 1 0
0 0 0 1
Полезно обратить внимание на место знака « - » в каждой из трех приведенных матриц.
Б.
Матрица растяжения-сжатия:
a 0 0 0
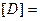
0 b 0 0 0 0 g 0
0 0 0 1
где
a > 0 – коэффицент растяжения (сжатия) вдоль оси абсцисс;
b > 0 – коэффицент растяжения (сжатия) вдоль оси ординат;
g > 0 – коэффицент растяжения (сжатия) вдоль оси аппликат.
В.
Матрицы отражения
Матрица отражения относительно плоскости ху:
 1 0 0 0 1 0 0 0
0 1 0 0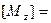 0 0 -1 0 0 0 -1 0
0 0 0 1
Матрица отражения относительно плоскости yz:
-1 0 0 0
0 1 0 0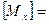 0 0 1 0 0 0 1 0
0 0 0 1
Матрица отражения относительно плоскости zx:
1 0 0 0
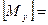
0 -1 0 0 0 0 1 0
0 0 0 1
Г.
Матрица переноса (здесь (l, m, n) - вектор переноса):
1 0 0 0
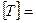
0 1 0 0 0 0 1 0
l m n 1
Как и в двумерном случае, все выписанные матрицы невырождены.
Приведем важный пример построения матрицы сложного преобразования по его геометрическому описанию.
Пример 3.
Построить матрицу вращения на угол j вокруг прямой L, проходящей через точку А (a, b, c) и имеющую направляющий вектор (l, m, n). Можно считать, что направляющий вектор прямой является единичным:
l2
+ m2
+ n2
= 1
На рис. 13 схематично показано, матрицу какого преобразования требуется найти.
 
  L L
X
Решение сформулированной задачи разбивается на несколько шагов. Опишем последовательно каждый из них.
1-й шаг.
Перенос на вектор –А (-a, -b, -c) при помощи матрицы

1 0 0 0
0 1 0 0 0 0 1 0
-a -b -c 1
В результате этого переноса мы добиваемся того, чтобы прямая L проходила через начало координат.
2-й шаг.
Совмещение оси аппликат прямой L двумя поворотами вокруг оси абсцисс и оси ординат.
1-й поворот – вокруг оси абсцисс на угол y (подлежащий определению). Чтобы найти этот угол, рассмотрим ортогональную проекцию L’ исходной прямой L на плоскость X = 0 (рис. 14).
  L’ Lq L’ LqY
   Y Y

0
Направляющий вектор прямой L’ определяется просто – он равен
(0, m, n).
Отсюда сразу же вытекает, что
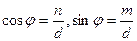 (4.10) (4.10)
где 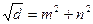  (4.11) (4.11)
Соответствующая матрица вращения имеет следующий вид:

1 0 0 0
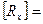 0 n/dm/d 0 0 n/dm/d 0
0 -m/dn/d 0 0 0 0 1
Под действием преобразования, описываемого этой матрицей, координаты вектора (l, m, n) изменятся. Подсчитав их, в результате получим
(l
,
m, n, 1)[ Rx
] = (l
, 0, d, 1). (4.13)
2-й поворот вокруг оси оси ординат на угол q, определяемый соотношениями
сosq = l
,
sinq = -d (4.14)
соответствующая матрица вращения записывается в следующем виде:
 l
0 d 0 l
0 d 0
0 1 0 0-d 0 l
0
0 0 0 1
3-й шаг.
Вращение вокруг прямой L на заданный угол j.
Так как теперь прямая L совпадает с осью аппликат, то соответствующая матрица имеет следующий вид:

cos j sin j 0 0
-sin j cos j 0 00 0 1 0
0 0 0 1
4-
й
шаг
.
Поворот вокруг оси ординат на угол -q.
5-й шаг.
Поворот вокруг оси абсцисс на угол -y.
Однако вращение в пространстве некоммутативно. Поэтому порядок, в котором проводятся вращения, является весьма существенным.
6-й шаг.
Перенос на вектор А (a, b, c).
Перемножив найденные матрицы в порядке их построения, получим следующую матрицу:
[ T ][ Rx
][ Ry
][ Rz
][ Ry
]-1
[ Rx
]-1
[ T ]-1
.
Выпишем окончательный результат, считая для простоты, что ось вращения ходит через начальную точку.

l
2
+ cosj(1 – l
2
) l
(1 – cosj)m + nsinj l
(1 – cosj)n – msinj 0
l
(1 – cosj)m – nsinj m2
+ cosj(1 – m2
) m(1 – cosj)n + l
sinj 0
l
(1 – cosj)n + msinj m(1 – cosj)n – l
sinj n2
+ cosj(1 - n2
) 0
0 0 0 1
Рассматривая примеры подобного рода, мы будем получать в результате невырожденные матрицы вида

a1
a2
a3
0
b1
b2
b3
0g1
g2
g3
0
l m n 1
При помощи таких матриц можно преобразовать любые плоские и пространственные фигуры.
Пример 4.
Требуется подвергнуть заданному аффинному преобразованию выпуклый многогранник.
Для этого сначала по геометрическому описанию отображения находим его матрицу [ A ]. Замечая далее, что произвольный выпуклый многогранник однозначно задается набором всех своих вершин
Vi
( xi
, yi
, zi
), i = 1,…,n,
Строим матрицу

x1
y1
z1
1
V = . . . . . . . . . . (4.18)
xn
yn
zn
1
Подвергая этот набор преобразованию, описываемому найденной невырожденной матрицей четвертого порядка, [ V ][ A ], мы получаем набор вершин нового выпуклого многогранника – образа исходного (рис. 15).
   Z Z
 0 0
Y
X

2.4. Формула обратного преобразования
В предыдущем параграфе нами была найдена формула (4) преобразования, обратного аффинному преобразованию (2). Покажем, что данное преобразование также является аффинным. Для этого достаточно доказать, что его определитель не равен нулю.
Рассмотрим определитель преобразования (4), он равен: 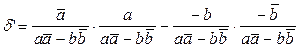 , приведём к общему знаменателю и сократим на общий множитель, получим: , приведём к общему знаменателю и сократим на общий множитель, получим: 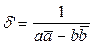 , где , где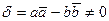 , следовательно, определитель обратного преобразования (4) находится в следующей зависимости с определителем преобразования (2): , следовательно, определитель обратного преобразования (4) находится в следующей зависимости с определителем преобразования (2): 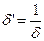 и он не равен нулю. Следовательно, обратное преобразование (4) также является аффинным, что и требовалось доказать. и он не равен нулю. Следовательно, обратное преобразование (4) также является аффинным, что и требовалось доказать.
2.5. Основная теорема теории аффинных преобразований
Докажем следующую теорему:
Существует одно и только одно аффинное преобразование, переводящее произвольные три точки А, В, С, не лежащие на одной прямой, в три произвольные точки А’, B', C', также не лежащие на одной прямой.
[3]
Доказать единственность аффинного преобразования можно показав, что коэффициенты преобразования a
,
b
, иc
выражаются однозначно через координаты точек А(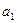 ), В( ), В(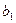 ), С( ), С(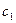 )
и A'(
a
’),
B
’(
b
’), C’(
c
’). )
и A'(
a
’),
B
’(
b
’), C’(
c
’).
Так как точки A', B', C'
являются образами точек А, В
и С
, то их координаты можно выразить следующим образом: 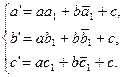
Решим эту систему относительно коэффициентов преобразования a, b, c
, получим их выражение через координаты точек А, В, С
и A',
B
’, C’
:
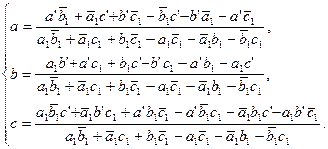
Таким образом, коэффициенты преобразования находятся однозначно. Опустив громоздкие выкладки, отметим, что определитель рассмотренного аффинного преобразования не равен нулю, таким образом, доказано существование и единственность искомого аффинного преобразования.
Глава III. Частные виды аффинных преобразований в сопряжённых комплексных координатах
3.1
. Преобразование подобия
Преобразованием подобия
(или подобием
) называется преобразование, которое каждые две точки P
иQ
отображает в такие две точки P
’
иQ
’
, что P
’
Q
’=
k
·
PQ
, где k
- постоянное действительное положительное число, называемое коэффициентом подобия
. [2]
Введём в рассмотрение аффинное преобразование (2). Рассмотрим неколлинеарные точки M
(
z
),
P
(
p
),
Q
(
q
)
и их образы M
’(
z
’),
P
’(
p
’),
Q
’(
q
’)
при некотором аффинном преобразовании (2). Преобразование подобия задаётся тремя парами точек M
"
M
’,
P
"
P
’,
Q
"
Q
’
так, что треугольник M
’
P
’
Q
’
подобен треугольнику MPQ
.
Существует два рода преобразований подобия. Подобие первого рода
сохраняет ориентацию каждого отображаемого треугольника, а подобие второго рода
отображает каждый треугольник в треугольник, противоположно ориентированный с ним. Рассмотрим теперь подобие каждого рода отдельно.
I. Пусть MPQ
и M
’
P
’
Q
’
– одинаково ориентированные подобные треугольники, тогда выполняются равенства 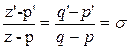 , где , где 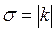 . .
Рассмотрим равенство 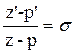 , откуда , откуда 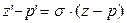 , тогда , тогда 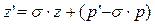 . Обозначим второе слагаемое как . Обозначим второе слагаемое как 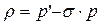 , получим равенство, задающее преобразование подобия первого рода
: , получим равенство, задающее преобразование подобия первого рода
:
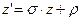 , где , где 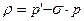 . (18) . (18)
II. Рассмотрим теперь подобные и противоположно ориентированные треугольники MPQ
и M
’
P
’
Q
’
. Для них верны равенства: 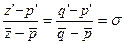 , где , где  . Рассмотрим равенство . Рассмотрим равенство 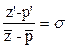 , преобразуем его к виду , преобразуем его к виду 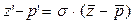 , тогда можем выразить z
’
: , тогда можем выразить z
’
: 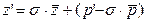 , обозначим второе слагаемое за ρ
, тогда получим равенство, которым задаётся преобразование подобия второго рода , обозначим второе слагаемое за ρ
, тогда получим равенство, которым задаётся преобразование подобия второго рода
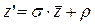 , где , где 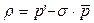 (19) (19)
3.2. Преобразование родства
3.2.1. Понятие преобразования родства
Родство
– аффинное преобразование, имеющее прямую неподвижных точек. Его задаёт формула:
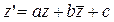 , где , где 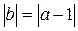 , ,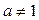 , ,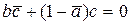 (20) (20)
Осью этого преобразования является прямая 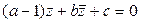 , примем её за действительную ось Ох
: , примем её за действительную ось Ох
: 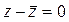 [1]. Тогда очевидно, что с=0
и b
=1-
a
. Поэтому преобразование (20) с действительной осью записывается формулой: [1]. Тогда очевидно, что с=0
и b
=1-
a
. Поэтому преобразование (20) с действительной осью записывается формулой:
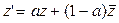 , где , где 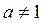 (21) (21)
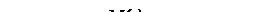
Выясним особенности этого преобразования. Перепишем его следующим образом 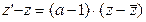 (22) составим из этого выражения и сопряжённого к нему выражения пропорцию (22) составим из этого выражения и сопряжённого к нему выражения пропорцию 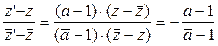 . Откуда . Откуда 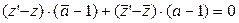 , а это является условием того, что векторы с координатами , а это является условием того, что векторы с координатами 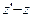 и и 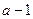 перпендикулярны. Так как а-1
– постоянные вектор, а z
и z
’
– координаты соответственных точек М
и М’
при аффинном преобразовании (рис. 17
), то все прямые, соединяющие точки М
и М’
будут параллельны между собой и параллельны некоторому вектору перпендикулярны. Так как а-1
– постоянные вектор, а z
и z
’
– координаты соответственных точек М
и М’
при аффинном преобразовании (рис. 17
), то все прямые, соединяющие точки М
и М’
будут параллельны между собой и параллельны некоторому вектору  с координатой (а-1)
i
, называемому направлением аффинного преобразования
, в данном случае – родства. с координатой (а-1)
i
, называемому направлением аффинного преобразования
, в данном случае – родства.
Если (а-1)
– чисто мнимое число (то есть 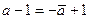 , откуда , откуда 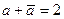 ), то направление родства будет коллинеарно оси родства. В этом случае аффинное преобразование называется сдвигом вдоль прямой
и условия, которые его задают, имеют вид ), то направление родства будет коллинеарно оси родства. В этом случае аффинное преобразование называется сдвигом вдоль прямой
и условия, которые его задают, имеют вид 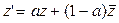 , , 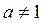 , , 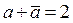 (23) (23)
Если же направление аффинного преобразования не совпадает с направлением его оси, то оно называется сжатием к прямой
и его задают следующие условия: 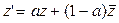 , , 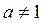 , , 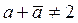 (24) (24)
3.2.2. Сжатие и его частные виды
Найдём собственные числа λ
преобразования сжатия (24) из условия 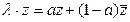 . Составим систему из этого условия и сопряжённого к нему выражения : . Составим систему из этого условия и сопряжённого к нему выражения : 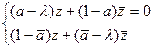 . Чтобы найти собственные числа, нужно решить уравнение . Чтобы найти собственные числа, нужно решить уравнение 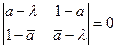 , откуда получим , откуда получим 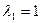 и и 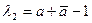 . .
Примем без доказательства следующую теорему
[1]: если λ – собственное действительное число аффинного преобразования, то множество точек, каждая из которых делит в отношении
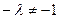 отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.
отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.

Очевидно, что прямые MM
’
и NN
’
(рис.18
) являются двойными прямыми и λ2
– действительное число, то точка Р
делит отрезок MM
’
в отношении 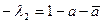 , то есть , то есть 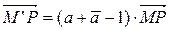 . Число . Число 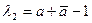 =δ
называется коэффициентом сжатия
. Если а
– действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием
. =δ
называется коэффициентом сжатия
. Если а
– действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием
.
Рассмотрим частный случай сжатия – косую симметрию
[1]. Это инволютивное преобразование, то есть оно тождественно преобразованию, обратному ему. Преобразование, обратное (24), имеет формулу:
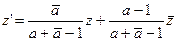 (25) (25)
Оно имеет ту же ось, что и (24). Равенство преобразований (24) и (25) имеет место тогда и только тогда, когда 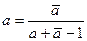 , откуда , откуда 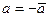 , то есть а
– чисто мнимое число. Таким образом, формулой (24) при условии , то есть а
– чисто мнимое число. Таким образом, формулой (24) при условии 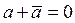 задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен 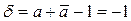 , следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки.
Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен. , следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки.
Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.
Если а=0
, получаем осевую
симметрию
относительно действительной оси. Осевая симметрия – аффинное преобразование также второго рода (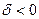 ). ).
Список литературы:
1. Скопец З.А. Геометрические миниатюры / Сост. Г.Д. Глейзер. – М.: Просвещение, 1990
2. Яглом И.М., Ашкинузе В.Г. Идеи и методы аффинной и проективной геометрии. Часть 1. Аффинная геометрия. М.: - Учпедгиз, 1962
3. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. - 6-е изд., перераб. - М.: Наука, 1988.
4. Умное А.Е. Аналитическая геометрия и линейная алгебра. - Долгопрудный: ЗАО Оптимизационные системы и технологии, 1997.
5. Кострикин А.И. Введение в алгебру. -М.: Наука, 1975.
6. Мальцев А.И. Основы линейной алгебры. - 4-е изд. -М.: Наука, 1976.
7. Постников М.М. Лекции по геометрии. Семестр 2. -М.: Наука, 1979.
8. Чехлов В. И. Лекции по аналитической геометрии и линейной алгебре. - М.: МФТИ, 2000.
9. Шарипов Р. А. Курс линейной алгебры и многомерной геометрии: учебное пособие для вузов / Издание Башкирского ун-та. ≈ Уфа, 1996. ≈ 226 с. ≈ ISBN 5-7477-0099-5
10. Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. — М.: Наука, 1964.
11. Ильин В. А., Поэняк Э. Г. Аналитическая геометрия. — М.: Наука, 1981.
12. Цубербиллер О. Н. Задачи и упражнения по аналитической геометрии. — М.: Наука, 1970.
|