Доказательство теоремы Ферма методами элементарной алгебры
Бобров А.В.
г. Москва
Контактный телефон – 8 (495)193-42-34
bobrov-baltika@mail.ru
В теореме Ферма утверждается, что равенство 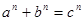 для натуральных для натуральных 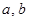 и и 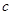 может иметь место только для целых может иметь место только для целых 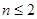 . .
Рассмотрим равенство
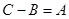 , (1) , (1)
где 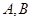 и и 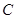 - натуральные взаимно простые числа, то есть числа, не имеющие общих целых множителей, кроме 1
. В этом случае два числа всегда нечетные. Пусть - натуральные взаимно простые числа, то есть числа, не имеющие общих целых множителей, кроме 1
. В этом случае два числа всегда нечетные. Пусть 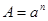 - нечетное число, - нечетное число, 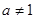 и и 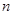 - натуральные числа. Для всякого действительного положительного числа выполнима операция нахождения арифметического значения корня, то есть равенство (1) можно записать в виде: - натуральные числа. Для всякого действительного положительного числа выполнима операция нахождения арифметического значения корня, то есть равенство (1) можно записать в виде:
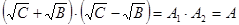  , (2) , (2)
где 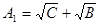 и и 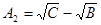 - действительные положительные множители числа - действительные положительные множители числа 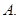 В соответствии со свойствами показательной функции, для любого В соответствии со свойствами показательной функции, для любого
из действительных положительных чисел 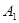 и и 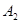 существуют единственные значения чисел существуют единственные значения чисел 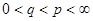 , удовлетворяющие равенствам , удовлетворяющие равенствам
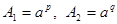 , (3) , (3)
Из равенств (2) и (3) следует:
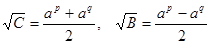 , , 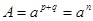 . (4) . (4)
Поскольку p
>
q
,
всегда имеет место p
-
q
=
k
, или а
p
= а
k∙
×а
q
,
то есть числа 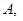 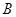 и и 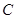 содержат общий множитель содержат общий множитель 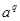 , что противоречит условию их взаимной простоты. Это условие выполнимо только при , что противоречит условию их взаимной простоты. Это условие выполнимо только при 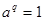 , то есть при , то есть при 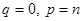 . Тогда равенства (4) принимают вид: . Тогда равенства (4) принимают вид:
 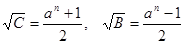 , , 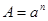 (5) (5)
откуда следует
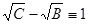 , (6) , (6)
то есть для взаимно простых 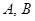 и и 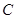 числа числа 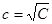 и и 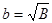 всегда являются двумя последовательными целыми числами. Еще Эвклидом доказано, что всякое нечетное число выражается, как разность квадратов двух последовательных целых чисел, то есть равенство (1) для натуральных взаимно простых всегда являются двумя последовательными целыми числами. Еще Эвклидом доказано, что всякое нечетное число выражается, как разность квадратов двух последовательных целых чисел, то есть равенство (1) для натуральных взаимно простых 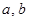 и и 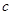 может быть выражено только в виде равенства может быть выражено только в виде равенства
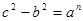 . (7) . (7)
Справедливость приведенного доказательства можно проиллюстрировать следующим примером.
Пусть в равенстве Ферма числа 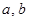 и и 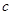 – целые взаимно простые, – целые взаимно простые, 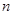 – четное. Тогда числа – четное. Тогда числа 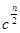 , ,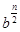 , их сумма , их сумма 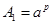 иразность иразность 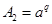 - также целые, показатель степени p
>
q
. - также целые, показатель степени p
>
q
.
Целые числа  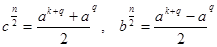 и и 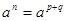
являются взаимно простыми, если не содержат общих целых множителей, кроме 1. Это условие выполнимо только тогда, когда общий целый множитель 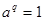 , то есть , то есть 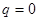 , , 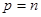 . .
Тогда разность 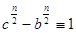  , что для одновременно целых , что для одновременно целых 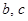 и и 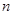 может иметь место может иметь место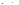 только при только при 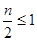 , то есть при , то есть при 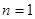 или или 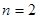 , что и позволило Пьеру де Ферма сделать почти 370 лет назад свою запись на полях арифметики Диофанта. , что и позволило Пьеру де Ферма сделать почти 370 лет назад свою запись на полях арифметики Диофанта.
|