Реферат: Биологическое время и его моделирование в квазихимическом пространстве

.

Методология построения теории времени естественных объектов, детально изложена [1, 2]. В данной работе рассмотрены компоненты этой теории на примере клеточной популяции.

1. Структура клеточной популяции. (O -компонент теории, object ).

Первая проблема состоит в выборе составных частей (элементов, таксонов, униструктур) объекта и определении их пространственных границ [3, 4].

Принципиальная трудность состоит в том, что строгий критерий членения объекта на части отсутствует. Выделение объектов природы – идеализация, связанная, главным образом, с особенностями информационных взаимодействий живых организмов со средой [5].

Объективным критерием членения объекта может служить принцип энергетической дифференцировки [6], который можно записать в виде:

Е_j+1 << Е_j ,

где Е_j , Е_j+1 — прочность связи между элементами уровня j и между элементами более высокого уровня j+1 (схема 1).

Для клеточной популяции порядок элементов с усложнением уровня (цифры - номера j уровней) можно представить в виде:

1 молекулы(t _m )I 2 органеллы(t _o ) I 3 клетки (t _c ) I 4 популяция(t _p ) I 5 экосистема(t _e ) (1)

Каждый уровень j разбивается на подмножества элементов (схема 1).

Схема 1. Иерархия подсистем естественных объектов

В качестве высшего уровня в данной иерархии определена экосистема. В случае клеточной монокультуры экосистема состоит из двух частей: клеточной популяции и культуральной среды. Соответственно, в описание структуры объекта необходимо вводить описание структуры среды. В частности химическая структура среды включает набор питательных веществ (субстратов) и химических агентов:

где M_s , X_s - векторы (наборы) субстратов (M_s1 , M_se ) и химических агентов (X_s1 ,X_se ) для биологического вида S.

Многомерность структуры (1-3) создает слишком большие сложности не только для количественной, но и для качественной идентификации модели. Поэтому целесообразно исследовать агрегированные модели. В случае клеточной монокультуры весьма информативной оказывается структура (1) из трех уровней:

Описательная модель клеточного цикла [7], начиная с митоза C_m , может быть представлена в виде разветвленной цепи:

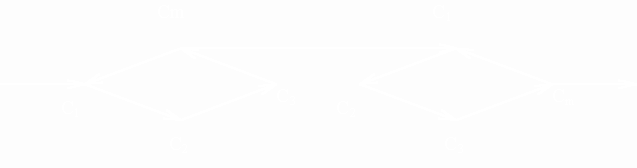(5a)

или в более сжатом варианте:

Здесь C₁ - молодая клетка непосредственно после деления, f - коэффициент размножения, который в общем случае может отличаться от 2. С₂ , С ₃ , С_m - фазы развития каждой из f клеток C₁ .

Фазы C₁ , C₂ , C₃ , C_m соответствуют стадиям клеточного цикла G₁ , S, G₂ , M (клетки четырех возрастов) и являются подмножествами 4-го уровня иерархии (4) - популяции. Популяция с наборами химических агентов (2) и (3) формирует 5-й уровень модели (4).

2. Пространство допустимых состояний популяции (S-компонент теории, states ).

Состояние системы отображается набором элементов (универсумов) всех типов (схема 1). В полной модели (2) состояние клеточной монокультуры задается числами всех типов мономеров, полимеров, органелл, клеток, химических и физических агентов среды. Размерность пространства состояний даже для культуры прокариотов составляет весьма большую величину.

Ограничения на достижимые состояния определяются условиями положительности числа компонентов и физической емкости среды.

В модели (4) состояние задается числами всех типов клеток, химических и физических агентов среды. Уменьшение размерности модели достигается путем аггрегирования разных элементов одного уровня по тому или иному признаку.

Например, в рассматриваемой ниже двухстадийной модели фазы C₁ , C₂ , C₃ объединяются в одну по признаку их большой длительности и отсутствия деления на этих стадиях цикла. Разветвленный циклический граф, отображающий эту двухстадийную модель, имеет вид:

(5c)

3. Изменение состояний популяции, «предвремя» ( C-компонент теории, change).

Разбиение множества особей на возрастные подмножества зависит от критериев, заложенных в основу членения объекта по данному признаку, от разрешающей способности экспериментальной методики и других факторов. Это обстоятельство хорошо иллюстрируется общепринятым членением клеточной популяции на четыре стадии (фазы) развития клеток C₁ , С₂ , С ₃ , С_m (G₁ , S, G₂ , M). Мало вероятно, что в природе существуют хотя бы две клетки, идентичных по наборам элементов всех уровней. Поэтому отнесение данной клетки к той или иной стадии проводится по степени соответствия индивидуальных характеристик этой клетки и усредненных характеристик стадий.

В результате метаболизма данная клетка практически непрерывно меняет набор элементов (1) и движется по своей индивидуальной траектории в определенном выше пространстве состояний (S-компонент теории). Эта траектория описывает все стадии развития данной клетки (движение в фазовом пространстве) от деления до деления. Последовательность точек этой фазовой траектории, отображенная на числовую ось, определяет предвремя индивидуальной клетки.

Траектории всех клеток популяции образуют в фазовом пространстве пучок. Отображение этого пучка на множество усредненных характеристик дает усредненную фазовую траекторию популяции. Последовательность точек этой траектории, отображенная на числовую ось, определяет предвремя популяции.

Дальнейшая редукция модели приводит к цепи последовательных стадий (5b), представляющей собой разветвленный циклический граф.

4.Часы и параметрическое время популяции (T-компонент теории, time).

Проблема выбора временных границ существования объекта тесно связана с C-компонентом теории, с определением масштабов предвремени, границ в пространстве.

Событие (момент времени) – переход объекта из одного состояния в другое. Тип события определяется уровнем, на котором оно происходит [2].

Предвремя природного объекта – отношение порядка (refl+trans) на множестве событий в этом объекте. Отображением этого порядка на числовой ряд получают числовое выражение предвремени.

Время – интервал между двумя наблюдаемыми событиями одного типа. Измеряется время числом событий между этими двумя событиями.

С биологической точки зрения возраст особи соответствует некоторой стадии индивидуального развития, начиная от зарождения. Стадия развития биологического объекта – синоним его возраста или биологического времени В общем случае возраст однозначно не связан с физическим временем. Исходя из этого и вводят понятие биологического времени.

Экспликацию понятия “биологическое время” целесообразно дать на примере клеточных популяций. Возраст популяции t_p определяется средним числом делений N_d первичных клеток посева или, что то же самое, числом циклов в цепи (5): t_p порядка t_c N_d , где t _c - среднее время клеточного цикла.

Каждую из биохимических реакций можно трактовать как замену одних молекул другими на молекулярном уровне структурной иерархии (1). Такая замена осуществляется в результате атомно-молекулярных взаимодействий. Поэтому естественным эталоном времени на молекулярном уровне являются атомные часы. Соответственно временные интервалы между «химическими» событиями измеряются в шкале физического времени. Характерное время t_m молекулярного уровня определяется скоростями ферментативных реакций. Интервалы между событиями на молекулярном уровне имеют значения порядка секунд.

«Химические» события предопределяют события на всех более высоких уровнях популяции. Поэтому временные интервалы на этих уровнях обычно также измеряются в шкале физического времени.

Органеллы собираются из большого числа молекул. Сборка органелл осуществляется в результате молекулярных и, в том числе, ферментативных взаимодействий. Временные интервалы органелл t_o имеют значения порядка 10² с.

Клетки формируются в результате образования наборов органелл и молекул и их трансформации. Временные интервалы клеток t_c имеют значения порядка 10⁴ с.

Популяция развивается в результате изменения наборов клеток в разных фазах развития. Взаимодействия между клетками носят диффузионно-обменный и контактный характер. Временные интервалы популяции t_p порядка 10⁵ с.

Динамика экосистемы зависит от запаса ресурсов, емкости, открытости а также от характера взаимодействия популяции со средой. Временные интервалы экосистемы t_e имеют значения порядка t_p .

Таким образом, для описания движения на всех уровнях популяции может использоваться единая физическая шкала времени.

5.Закон обобщенного движения популяции (L-компонент теории, law) .

Для вывода закона обобщенного движения популяции в пространстве состояний предлагается использовать единый «квазихимический» язык для описания событий на всех уровнях популяции. При этом все взаимодействия отображаются квазихимическими уравнениями [5, 8, 9]. Пространство состояний при таком описании можно назвать квазихимическим .

Отобразим с помощью квазихимических уравнений события, определяющие рост популяции на клеточном уровне трехуровневой модели (5).

Популяция развивается в результате усвоения субстратов. Это развитие описывается системой квазихимических реакций (индекс s опускается):

Набор кинетических констант (p₁₁ , p_ne ) определяет кинетический вектор роста.

Действие токсикантов Х_i , может проявляться на любой стадии роста и описывается сходным образом:

Здесь (C_k X_l ) – дезактивированные клетки разных стадий, (X₁ ,X_t ) – вектор токсикантов; {d_ij } – матрица коэффициентов ингибирования, (r_x1 , r_xt ) - вектор скоростей притока токсикантов из среды.

Кроме того, следует учесть клеточные взаимодействия (автоингибирование). Например, зрелые особи C_i переводят в неактивное состояние молодых C_ak :

Взаимодействия клеток описываются кинетическим вектором автоингибировния (a_i1 ,…, a_im ).

В открытых системах учитывается взаимодействие экосистемы со средой ЕЕ:

где (w₁ ,…, w_n ) - вектор скоростей притока особей С₁ ,…, С_n из среды.

Система псевдохимических реакций (6)-(9) описывается стандартным образом [10-12] системой кинетических уравнений, представляющих собой закон обобщенного движения популяции в пространстве состояний:

dC /dt = S KC - S ACC - S DCX + S R + S W

(10)

Здесь C = (c₁ , c₂ , c₃ , c_m ) вектор количества клеток в разных фазах, K , A , D , R , W – матрицы кинетических параметров.

С помощью различных приближений [11] система уравнений четвертого порядка может быть редуцирована до второго. Такая система достаточно информативна и позволяет качественно, а во многих случаях и количественно, описать развитие популяций различных видов.

Рассмотрим редуцированную модель (1) из двух стадий – роста и деления, дополненных стадией самоингибирования:

Здесь использованы те же обозначения, что и в системах (6) – (9) (индексы опущены): С₁ – множество клеток разного возраста до митоза, С_m – митотические клетки; C_a – клетки в анабиозе; (C_k X_l ) – ингибированные клетки разных стадий; M₁ , M₂ –субстраты.

Следует отметить, что двухстадийный цикл (фазы S и M) наблюдается на ранних стадиях развития зародышей пойкилотермных животных [15, 16]. На этом основании в этот период в качестве единичного интервала времени можно использовать длительность t_c клеточного цикла («детлаф»).

В предположении постоянства концентраций субстратов М₁ , М₂ кинетика цепного роста популяции, состоящей из особей С₁ и С_m , описывается системой:

Здесь c₁ , c_m – количества растущих и митотические клеток; a, b, p –коэффициенты автоингибирования, рождения и роста популяции в отсутствии ингибиторов. В коэффициенты р и b включены постоянные количества субстратов М₁ и М₂ . f - коэффициент размножения. Коэффициенты b_x и p_x – функции количества ингибиторов x₁ и x₂ :

Система уравнений (12) представляет собой закон обобщенного движения двухстадийной популяции в пространстве состояний. Преобразованная в виде:

система (12) определяет соотношение между интервалами биологического dc_i и физического dt времени.

В приближении квазистационарности для митотических клеток С_m система (12.1-12.2) сводится к одному уравнению:

Динамику численности популяции с₁ (t) в общем случае нельзя выразить в виде явной функции от времени t. Поэтому используют обратную функцию t(c₁ ), получаемую интегрированием (14) по с₁ :

Уравнение (16) в явном виде отображает физическое время на множество состояний популяции.

6. Интерпретация модели (I-компонент теории, interpretation).

На рис.1 приведены экспериментальные точки и графики функции (16), описывающие дрожжевых клеток в присутствии солей хрома и никеля [13]. При расчете графиков брали значения a, b, р , f, определенные по экспериментальным данным [17]. В пределах точности измерений расчетные кривые согласуются с экспериментом при измененении численности примерно на шесть порядков.

Хорошее согласие теории с экспериментом получено и для других биологических объектов [8, 9]. Поэтому интересно провести верификацию квазихимической модели по характеристикам, связанным с проблемами биологического времени.

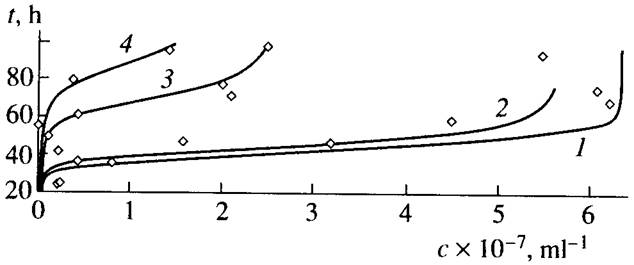
Рис.1. Экспериментальные точки и графики функции (16), описывающие рост пивных дрожжей при разных концентрациях (ммоль/л) солей хрома и никеля [13]: (1) c(Ni) = c(Cr) = 0.0, (2) c(Ni) = 0.5, (3) c(Cr) = 0.5, and (4) c(Ni) + c(Cr) = 0.5 + 0.5. Коэффициенты: a=1.25.10^-7 мл /ч, b=0.8ч^-1 , р=0.32 ч^-1 , f =2.

Уравнения (12a) можно представить в виде:

где величины K_c1 =(-p_x c₁ +f b c_m +w₁ )и K_cm = (p c₁ -b_x c_m -a c₁ c_m )представляют собой калибровочные коэффициенты для перехода от интервала физического времени dt к интервалам биологического времени dc_j .

На основе (17) получают соотношение между конечными временными интервалами:

D c1 =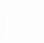c1 dt, D cm =ИНТЕГРАЛ( Kcm dt ).

( 17а)

Калибровочные соотношения (17) обладают следующими свойствами:

1. Коэффициенты K_c1 и K_cm зависят от кинетических констант, характеризующих внутри- и внесистемные взаимодействия. Это определяет специфику биологического времени данного объекта.

2. Коэффициенты K_c1 и K_cm зависят от наблюдаемого состояния объекта, то есть изменяются при движении по фазовой траектории.

3. Коэффициенты K_c1 и K_cm неодинаковы для однотипных элементов данного уровня иерархии. Это означает, что собственное время «течет» с разной скоростью не только на разных уровнях биологической системы, но и в различных элементах одного уровня.

Приращение суммарной массы dm_p или численности dN_p популяции определяют интервал биологического времени популяции в целом. Для двухстадийной популяции dN_p = V(с₁ +с_m ), где V – объем системы. Связь между популяционным и физическим временем согласно (17) определяется соотношением:

Через длительность клеточного цикла t_c в физической шкале (в «детлафах») эта величина выразится в виде:

Длительность клеточного цикла t_c в физической шкале рассчитывают либо по экпериментальным значениям прироста массы или численности клеток, либо по экпериментальным значениям параметров b и p модели (12).

Приращение численности популяции D с₁₂ =c₂ -c₁ в единице обьема наблюдается за время D t₁₂ =t₂ -t₁ , согласно (16) равное:

где c₁ ,c₂ – численности в моменты t₁ ,t₂ .

Среднее число делений n₁₂ каждой из c₁ клеток за это время равно:

Следователъно, t _c можно оценить по формуле:

Другую оценку значения t_c можно сделать по кинетическим коэффициентам b и p модели (12):

Расчет по по формулам (22) и (23) для дрожжей S. cerevisae (данные рис.1) дает близкие значения величины t_c ( 3,7 и 4,4 ч).

Формула (23) предлагаемой модели клеточной динамики позволяет количественно интерпретировать температурную зависимость длительности клеточного цикла t_c , хорошо известную из работ [14-16]. Зависимость коэффициентов b и p от температуры можно аппроксимировать формулой Аррениуса. Тогда согласно (23) температурная зависимость t_c выражается в виде:

где E_b , E_p – энергии активации скоростей деления и роста, a_b , a_b – соответствующие предэкспоненциальные множители, T – абсолютная температура.

На рис. 2а приведена кривая зависимости t_c , рассчитанная по уравнению (24) с помощью эмпирических параметров a_b , a_b и E_b , E_p . Модельная кривая качественно правильно описывает наблюдаемую закономерность [14- 16].

Подставляя аррениусовские выражения коэффициентов b и p в уравнение (20) получают формулу для расчета зависимости времени роста D t₁₂ популяции до разных ступеней развития (разные c₂ /c₁ ).

На рис. 2б приведены кривые зависимости D t₁₂ , рассчитанные по уравнению (20) с помощью эмпирических параметров a_b , a_b и E_b , E_p . Модельные кривые качественно правильно описывают экспериментально наблюдаемые зависимости [14-16].

а) б)

Рис. 2. Кривые температурной зависимости длительности развития элементов разных уровней: а) длительность клеточного цикла, рассчитанная по уравнению (24); б) длительности разных стадий развития популяции, рассчитанные по уравнению (20).

Модель (12) дает возможность проверить для популяции применимость функции Бакмана [14]:

где H – скорость роста популяции, T – время роста, k < 0 –нормировочная постоянная.

В аналитическом виде функцию Бакмана можно получить, подставляя в (25) выражения H и T, равные, соответственно, правым частям уравнений (14) (при w₁ =0) и (16). При этом получают зависимость (25) как явную функцию роста, выражаемого переменной величиной c₁ при заданном начальном значении c₀ . На рис. 4 приведен соответствующий график. Согласно (25), логарифм скорости роста должен быть пропорционален квадрату логарифма времени роста. Однако, как следует из рис. 4, такая зависимость для двухстадийной популяции не наблюдается.

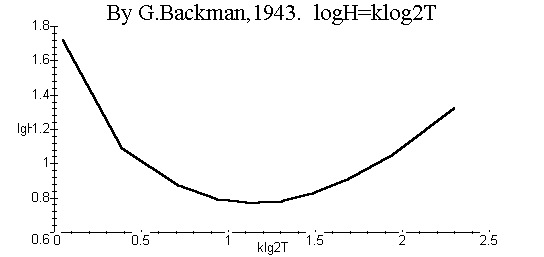
Рис. 3. Функция роста Бакмана (25), построенная на основе двухстадийной модели (16) динамики популяции.

ЛИТЕРАТУРА

1. Акчурин И.А. Единство естественнонаучного знания. М., 1974.

2. Левич А.П. // Конструкции времени в естествознании. М., 1996. С. 9-27, 235-288.

3. Шаров А.А. // Конструкции времени в естествознании. М., 1996. С. 96-111.

4. Мейен С.В. // Системность и эволюция. М., 1984. С. 7-32.

5. Ершов Ю.А .// Ж. Физ. химии. 1999. Т.73. № 10, с. 1817 – 1823.

6. Ершов Ю.А .// Ж. Физ. Химии, 2000, т. 74, № 6, с. 1087-1093.

7. Ершов Ю.А . Термодинамика квазиравновесий в биологических системах. М., ВИНИТИ, 1983. 140 с.

8. Гудвин Б . Аналитическая физиология клеток и развивающихся организмов. М.:Мир,1979,288 с.

9. Ершов Ю.А .// Докл. РАН. 1997. Т.72. № 5. с. 627-629.

10. Ершов Ю.А .// Ж. Физ. химии. 1998. Т. 352. № 3. с.553-559.

11. Ершов Ю.А. и др. Кинетика и термодинамика биохимических и физиологических процессов. М., Медицина,1990, 155с.

12. Романовский ю. м., Степанова Н.В., Чернавский Д.С. Математическая биофизика. М. Наука. 1984. - 304 с.

13. Математические проблемы химической кинетики. Сб. Ред. К.И. Замараев, Г.С. Яблонский. Новосибирск: Наука,1989, 335с.