|
Теоретическая часть
Практическая часть
Список литературы
Ясно объясните причины, лежащие в основе потребности в деньгах и ее удовлетворении и, используя график, объясните как экономисты – кенсианцы отличаются от монетаристов в определении эффективности денежной политики в достижении равновесия полной занятости
Что же такое деньги? Четкого, признаваемого всеми экономистами определения сущности денег, в общем-то, нет.
В марксистской трудовой теории стоимости мы можем найти такую дефиницию: деньги — это особый, общественно-признанный товар — всеобщий эквивалент.
Большинство же экономистов, занимавшихся и занимающихся вопросами теории денег, выводят их сущность из выполняемых деньгами функций и констатируют, что деньгами может быть все, что признается людьми за деньги и выполняет их функции. Среди современных экономистов существует несколько мнений по поводу числа и толкования функций денег, но единодушно признаются три основные: средство обращения, средство сохранения богатства (накопления), мера стоимости.
Выполняя функцию средства обращения, деньги выступают посредником при обмене товаров и услуг, благодаря чему преодолеваются индивидуальные, количественные, временные и пространственные границы, присущие бартеру. Кроме того, как отмечалось выше, сокращаются и издержки обращения. Эту функцию выполняют реальные деньги.
Деньги в функции меры стоимости позволяют выразить стоимость товаров (услуг) в терминах, известных каждому участнику товарообмена — в национальных денежных единицах. Денежные единицы используются как масштаб цен для соизмерения стоимости отдельных товаров и услуг, позволяя тем самым сориентироваться для принятия рациональных решений.
Средство сохранения стоимости (средство накопления) — это способность денег использовать соответствующую стоимость того, что было продано сегодня для будущей покупки. Эта функция денег является следствием их абсолютной ликвидности. Под абсолютной ликвидностью денег понимается то, что с их помощью владелец денег может в любой момент выполнить любое финансовое обязательство, поскольку деньги всегда могут быть использованы в качестве платежа и имеют фиксированную номинальную стоимость.
Реклама

Однако реальное выполнение деньгами этой функции имеет свои ограничения. Если номинальная стоимость денег фиксирована, то реальная их стоимость (покупательная способность) может меняться. Прежде всего, она зависит от цен на товары и услуги:
Z = 1 : Р
где Z — покупательная способность денег; Р — цены.
Так, в условиях инфляции реальная стоимость денег резко падает и сохранение богатства в виде денег теряет экономический смысл. Начинается погоня за менее ликвидными или вообще неликвидными, но реальными ценностями: идет скупка земельных участков, недвижимости, произведений искусства и т.д.
Кроме того, сохранение богатства в виде денег может привести к так называемым вмененным издержкам или издержкам упущенных возможностей, поскольку сохранение богатства в виде денег не приносит их владельцу процентного дохода за период хранения (по сравнению, например, с богатством в виде недвижимости, когда владелец дома, сдав его в аренду, получает доход в виде арендной платы и т.п.).
Выполняя названные функции, деньги играют важнейшую роль в рыночной экономике: они опосредуют кругооборот доходов и продуктов.
Американский экономист [Фишер (1993:37) сформулировал следующее уравнение обмена:
M·V=P·Q
где М — масса денег в обращении;
V — скорость обращения денег (среднегодовое количество оборотов, сделанных деньгами, которые находятся в обращении и используются на покупку конечных товаров и услуг или количество раз, которое денежная единица обменивалась на товары и услуги в течение года);
Р — средняя цена товаров и услуг,
Q — количество проданных товаров и оказанных услуг].
Иными словами, количество денег в обращении, умноженное на число их оборотов в актах купли-продажи за год, равняется объему валового национального продукта.
Уравнение обмена И.Фишера позволяет понять, почему колеблются цены и соответственно покупательная способность денег, объем реального национального продукта. Например, при постоянных V и Q изменение денежного предложения М будет прямо влиять на цены. Однако роста цен не произойдет, если увеличение денежного предложения будет происходить одновременно с расширением выпуска товаров и объема оказанных услуг в той же или большей степени.
Как мера стоимости деньги измеряют ценность всех благ. Определять цену любого товара можно с помощью идеальных денег, в качестве которых до 30-х гг. XX в. выступало золото, а в настоящее время используется обменный курс национальной валюты.
Реклама

Как средство обращения деньги выступают мимолетным посредником в сделках купли-продажи, что дает возможность использовать бумажные деньги. Если государство выпустит их сверх меры, то они обесценятся и будут замещены бартером. В конечном счете, обесценивание денег может привести к ограничению рыночных сделок с помощью карточек и талонов.
Деньги как средство платежа выражают отношения между должником и кредитором, так как акт купли-продажи часто бывает разорван во времени. Период оплаты товаров и услуг в этом случае по целому ряду причин не совпадает с поставкой продукции. Подобные сделки оформляются в виде долговых обязательств — векселей, банкнот, счетов, чеков и др. На их основе возникают кредитные деньги.
Деньги как средство накопления представляют собой запас финансовых ресурсов для будущих расходов, формируют сбережения домохозяйств и инвестиции предпринимателей.
Выполнение роли мировых денег состоит в том, что деньги функционируют в качестве средства обращения и средства платежа в международном экономическом обмене.
В экономической науке сложились три основные теории денег:
1. металлическая;
2. номиналистическая;
3. количественная.
Металлическая теория была разработана в рамках меркантилизма и сводила денежное обращение к двум функциям — средству накопления и мировым деньгам. Именно эти функции наиболее успешно выполняли благородные металлы, являясь олицетворением богатства нации.
Номиналистическая теория разрабатывалась классической школой в полемике со сторонниками металлической теории. Указывая на ограниченный подход меркантилистов к деньгам, сторонники этой теории впадали в другую крайность, абсолютизируя значение функций средства обращения и платежа и объявляя деньги чисто условными знаками, денежными единицами, которые участвовало государство.
Количественная теория денег возникла также в рамках классической школы. Постепенно она стала преобладать в экономической теории и развивалась даже в XX в. (уравнение количественной теории И. Фишера; кембриджское уравнение А. Лигу). Ее смысл сводится к тому, что деньги имеют стоимостную основу, поэтому их увеличение в экономике не приводит к росту национального богатства, а только к увеличению цен.
[Камаев (1999:341) отмечает, что в любой стране денежное обращение организуется государством на определенных принципах, т.е. в форме денежной системы]. Элементами денежной системы являются:
- национальная денежная единица (рубль, доллар, йена и т.д.), в которых выражаются цены на товары и услуги;
- виды денежных знаков в форме кредитных бумажных денег и бидонной разменной монеты, являющихся законным платежным средством в наличном обороте;
- организация эмиссии денег, т.е. порядок выпуска денег в обращение;
- государственные органы, регулирующие и контролирующие денежное обращение (учреждения Центрального банка страны, Министерство финансов, государственные казначейства).
В современных условиях денежное обращение не основано на золотом стандарте, а является системой бумажных кредитных денег.
Кредитные деньги, в свою очередь, породили систему кредитных карточек, которые с наступлением эры компьютеров породили так называемые «электронные деньги», выполняющие функции денег безбумажным способом, в виде сигналов ЭВМ.
Денежно-кредитная политика государства состоит в регулировании денежного обращения с целью оказания воздействия на рост производства и сдерживания инфляции и безработицы.
[Добрынин (2002:290) отмечает, что основным органом, реализующим эту политику, является Центральный банк страны, который должен:
- обеспечивать устойчивость национальной валюты;
- вырабатывать единые правила для денежного рынка и контролировать действия его агентов;
- осуществлять последовательную макроэкономическую политику, позволяющую задействовать разнообразные экономические регуляторы и стабилизаторы развития реального сектора экономики].
Для достижения перечисленных целей Центробанк манипулирует деньгами и кредитами.
В зависимости от экономической конъюнктуры Центральный банк проводит политику либо «дорогих», либо «дешевых» денег.
Если инфляция в стране приобретает опасные размеры, то Центральный банк ставит перед собой цель удержать денежную массу в существующих размерах, не допустить новой эмиссии денег. Тогда, несмотря на изменения в спросе на деньги, кривая совокупного предложения на рынке примет вертикальный вид (рис. 1).
  % MS % MS
 MD1 MD1
MD
 0 0
денежная масса
MD – денежная масса,
MD1
– перемещение денежной массы,
MS – предложение денег
Рис. 1. Жесткая денежная (монетарная) политика
В этом случае увеличение спроса на деньги вызовет рост процентной ставки (цены денег), что отрицательно скажется на инвестиционной активности предпринимательского сектора. Подобная денежная политика Центрального банка носит название жесткой монетарной политики с «дорогими» деньгами.
Если в стране необходимо создать благоприятные условия для инвестирования, то Центральный банк будет вынужден пожертвовать стабильностью денежной массы и станет контролировать уровень процентной ставки, не давая ему расти под влиянием спроса на деньги.
Такая денежная политика носит название гибкой монетарной политики, в основе которой лежат «дешевые» деньги (рис. 2).
 % %
    MS MS
 MD1 MD1
MD
 
0 денежная масса
MD – денежная масса,
MD1
– перемещение денежной массы,
MS – предложение денег
Рис. 2. Гибкая денежная (монетарная) политика
Если в стране ставится задача поддержки развития экономики или компенсируется замедление денежного оборота, то допускается одновременный рост денежной массы и процентной ставки.
Такую компромиссную политику принято называть промежуточной монетарной политикой.
[Фишер (1993:49) считает, что выбор Центральным банком той или иной политики в предложении денег зависит от причин, породивших изменения в спросе на деньги].
Совокупные спрос и предложение встречаются на рынке благ, формируя равновесную ситуацию: AD = AS.
В самом общем виде кривая AD пересекает AS на участке II, образуя равновесный объем национального производства (ВНП) и равновесную цену РЕ
.
Эта ситуация описывается графиком (рис. 3).
   Р AS Р AS
  РЕ
Е РЕ
Е
AD
 у у
уЕ
Рис. 3. Равновесие на рынке благ
Различные взгляды на кривую AS в коротком периоде приводят монетаристов и кейнсианцев к противоположной оценке макроэкономического равновесия на рынке благ. Представители монетаристской школы считают, что в условиях гибкости цен, зарплаты, процентной ставки они способны расти и сокращаться под влиянием спроса и предложения. В результате снижение AD не приводит к сокращению объема национального производства, а только изменяет цены. Отсюда делается вывод о том, что свободное ценообразование способно само, без всякого вмешательства государства, установить равновесие на рынке благ (рис. 4).
  Р AS Р AS
 РЕ
Е РЕ
Е
AD
 РЕ
1
Е1
AD1 РЕ
1
Е1
AD1

у у (ВНП)
Рис. 4. Монетаристская трактовка равновесия на рынке благ
Представители кейнсианской школы не признают такой оценки равновесия и предлагают свою: совокупное предложение AS лишь в длительном периоде имеет вертикальный вид, а в коротком — принимает горизонтальный: в экономике постоянно существуют незадействованные ресурсы (в том числе безработица), а цены и зарплата не являются гибкими, так как зафиксированы в договорах поставок продукции, закупленном сырье и оборудовании, заключенных трудовых соглашениях с работниками на длительный период (месяцы и годы) и т.д. (рис. 5).
   Р AS Р AS
   Е1
Е Е1
Е
AD
AD1

 уЕ
1
уЕ
у (ВНП) уЕ
1
уЕ
у (ВНП)
Рис. 5. Кейсианская трактовка равновесия на рынке благ
[Попов (2000:57) отмечает, что сокращение совокупного спроса AD ведет к сокращению объемов национального производства у (ВНП), поэтому, чтобы не допустить спада или даже кризиса в экономике, необходимо вмешательство государства с целью поддержки достаточного уровня совокупного спроса AD].
Классическая кривая совокупного предложения основана на предположении о том, что имеет место симметричная информация и все цены, включая номинальную заработную плату, являются абсолютно гибкими, как в краткосрочном, так и в долгосрочном периоде. В результате рынок труда всегда находиться в равновесии и всегда существует полная занятость рабочей силы. Как же при таких предпосылках будет выглядеть кривая совокупного предложения, связывающая выпуск с уровнем цен.
Рассмотрим некий исходный уровень цен P0
. При этом уровне цен на рынке труда будет достигнуто равновесие, если номинальная зарплата w0
будет такова, что реальная зарплата w0
/P0
будет равна равновесной реальной заработной плате (w/P), а занятость при этом будет равна L и, таким образом, уровню цен P0
будет соответствовать выпуск при полной занятости, который мы обозначаем через Yf.e.
Если уровень цен возрастет до P1
, то соответствующим образом изменится номинальная зарплата, а реальная заработная плата останется равной (w/P). В результате, по-прежнему, будет иметь место полная занятость, и выпуск останется прежним. Таким образом, мы получаем вертикальную кривую совокупного предложения (рис. 6), причем эта кривая имеет место одновременно в краткосрочном и долгосрочном периодах.
 Р Р

 Y Y
Yf.e
Рис. 6. Классическая кривая совокупного предложения
Итак, согласно классической теории, кривая совокупного предложения вертикальна.
Современная классическая теория подходит к вопросу о функционировании рынка труда несколько иначе. Неоклассики, по-прежнему, считают цены абсолютно гибкими, однако допускают наличие асимметричной информации в краткосрочном периоде. Итак, предположим, что фирмы, выбирая уровень занятости, ориентируются на действительный уровень цен данного периода, а рабочие не обладают этой информацией и их выбор предложения труда базируется лишь на ожидаемом уровне цен. В результате мы должны модифицировать графическое представление равновесия на рынке труда, поскольку агенты могут ориентироваться на разные уровни цен.
Изобразим кривые спроса и предложения труда, как функции от номинальной, а не реальной заработной платы. В этом случае кривая спроса на труд представляет произведение уровня цен на предельный продукт труда, и будет сдвигаться вверх/вниз при росте/падении уровня цен. Местоположение кривой предложения труда определяется ожидаемым уровнем цен. Так, рост ожидаемого уровня цен будет сдвигать эту кривую вверх и наоборот. Предположим, что в рассматриваемом периоде ожидаемый уровень цен (Pехр
) совпал с реальным уровнем цен P0
. В этом случае равновесие будет совпадать с равновесием в модели с симметричной информацией, и занятость будет равна L, а выпуск – Yf.e.
Что же произойдет, если в действительности уровень цен окажется выше ожидаемого рабочими: P1
> Pexp
=P0
. Кривая предложения останется на месте, а кривая спроса на труд сдвинется вверх, в результате, мы наблюдаем рост номинальной заработной платы и рост занятости.
Как же в результате изменилась реальная заработная плата? Очевидно, что она упала: w’/P1
<w0
/P0
(в противном случае величина спроса на труд не могла бы возрасти). Возникает вопрос, как возможен рост равновесной величины занятости, то есть, почему рабочие соглашаются работать больше при меньшей реальной заработной плате?
Этот парадокс объясняется асимметричной информацией. Рабочие наблюдают рост номинальной заработной платы, но не осознают, что при этом увеличился и уровень цен, поскольку они не могут наблюдать его в краткосрочном периоде и при принятии решений ориентируются лишь на ожидаемый уровень цен. В результате повышение номинальной заработной платы выступает для рабочих как повышение ожидаемой реальной заработной платы, что приводит к росту предложения труда и занятости в целом. Рост занятости, в свою очередь, означает рост выпуска, что дает кривую предложения с положительной зависимостью между выпуском и уровнем цен.
Заметим, что эта кривая соответствует определенному ожидаемому уровню цен. Если в следующем периоде рабочие пересмотрят свои ожидания в сторону повышения, то кривая краткосрочного предложения сдвинется вверх. И, наконец, при уровне цен, равном ожидаемому, мы будем иметь выпуск, соответствующий полной занятости.
Наличие асимметричной информации следует рассматривать лишь в краткосрочной перспективе. В долгосрочной перспективе ожидания соответствуют реальности, и мы имеем дело с классической вертикальной кривой совокупного предложения.
Теория предложения Фридмана-Фелпса основывалась на предположении о том, что фирмы обладают большим объемом информации по сравнению с рабочими. Обосновывалось это предположение тем, что фирмы интересуются лишь узким набором товаров и их ценами (ценами своей готовой продукции и ценами факторов производства), в результате фирмам значительно легче следить за изменением цен на интересующих их рынках, нежели рабочим, которым приходится иметь дело с большим разнообразием товаров и услуг. Адекватность подобной предпосылки вызывает определенные сомнения, поскольку работники сталкиваются с интересующими их товарами (и, соответственно ценами этих товаров) практически ежедневно, когда они делают покупки. Идея Фридмана о несовершенстве информации, как причине, порождающей положительную связь между уровнем цен и выпуском, получила дальнейшее развитие в работе Лукаса. Лукас привнес в модель Фридмана предпосылку о рациональных ожиданиях.
Экономические агенты имеют рациональные ожидания, если они делают наилучшие прогнозы при той информации, которой они обладают. Заметим, что эти прогнозы не обязаны всегда совпадать с действительностью, поскольку зачастую происходят непредвиденные события. Однако прогнозы должны быть корректны при отсутствии неожидаемых событий или «сюрпризов». Итак, рациональные ожидания означают, что люди не делают ошибок в прогнозах постоянно, то есть, в среднем прогнозы должны быть корректны. С этой точки зрения предпосылка Фридмана о том, что рабочие оказываются обманутыми, не вписывается в теорию рациональных ожиданий. Согласно идее Лукаса, на основе предыдущих периодов, когда рабочие оказывались обманутыми (то есть, когда рост занятости сопровождался падением реальной заработной платы) рабочие должны были сделать вывод о том, что предложение о дополнительной работе всегда сопровождается падением реальной заработной платы и, следовательно, не стоит соглашаться на эти предложения.
Рассмотрим модель, предложенную Лукасом. В соответствии с этой моделью фирмы наблюдают цены на своем рынке, а потому имеют точную информацию относительно изменения этих цен, но не могут при этом точно сказать, что происходит с уровнем цен в экономике в целом. Это означает, что фирмы не могут указать, например, причину роста цен на свою продукцию, поскольку это может быть как следствием роста спроса на их продукцию, так и результатом повышения уровня цен в экономике в целом. Эта неопределенность ставит фирмы в затруднительное положение, поскольку в первом случае фирмам следует наращивать выпуск, поскольку относительная цена выпускаемой продукции возросла, а во втором случае выпуск должен остаться неизменным. В силу неопределенности каждый раз, наблюдая рост цен на свою продукцию, фирма относит его с некоторой вероятностью к росту спроса на свой товар, а с некоторой вероятностью - к росту уровня цен, а потому повышает выпуск, но не очень сильно. Таким образом, на уровне экономики непредвиденный рост уровня цен в краткосрочном периоде ошибочно интерпретируется фирмами как рост спроса на их продукцию, побуждая увеличивать выпуск.
Традиционная кейнсианская теория предполагает негибкость уровня цен и номинальной заработной платы. Если номинальная зарплата фиксирована на уровне w0
, а производственная функция обладает постоянным предельным продуктом труда (MPL = a), то кривая предложения труда будет горизонтальной при уровне реальной заработной платы, равном предельному продукту труда w0
/P0
= MPL
=a .
Фиксированность номинальной заработной платы означает наличие безработицы, в силу чего занятость, а, следовательно, и выпуск определяются исключительно решением фирм, то есть спросом на труд. В результате, если уровень цен меньше P0
=w0
/a, то затраты на труд не покрываются отдачей от труда и фирмам невыгодно нанимать рабочих и производить продукт.
Итак, при цене, меньшей P0 выпуск равен нулю, а при цене равной P0
фирмы готовы производить сколь угодно много товара, в результате мы получаем горизонтальную кривую совокупного предложения при уровне цен P0.
Кейнсианское предположение об абсолютной негибкости цен и заработной платы выглядит реалистичным лишь в краткосрочном периоде. Современная кейнсианская теория строится на предположении о том, что номинальная заработная плата является фиксированной в краткосрочном периоде в силу того, что рабочие заранее подписывают контракт на определенный период времени, но зарплата может меняться при заключении нового контракта. При этом неокейнсианская теория не налагает никаких ограничений на предельный продукт труда, и соответственно, цены являются гибкими даже в краткосрочном периоде.
Как же выбирается уровень, на котором номинальная заработная плата будет зафиксирована в контракте. Он определяется, исходя из ожидаемого уровня цен и величины равновесной реальной заработной платы. Если мы обозначим равновесную реальную зарплату через (w/P), а ожидаемый уровень цен через p0
, то в контракте будет зафиксирована номинальная заработная плата w0
=P0
*(w/P)*. Такой выбор номинальной заработной платы означает, что в случае, если реальный уровень цен совпадет с ожидаемым, то будет иметь место полная занятость.
Согласно неокейнсианской теории, после заключения контракта, в котором фиксируется уровень номинальной заработной платы, уровень занятости определяется работодателем. Так, если в действительности уровень цен будет выше ожидаемого, то реальная заработная плата упадет и производителям будет выгодно увеличить занятость, что приведет к росту выпуска. Таким образом, неокейнсианская теория также как и неоклассическая приводит к положительно наклоненной кривой совокупного предложения. По истечении контракта, уровень номинальной заработной платы пересматривается в соответствии с новыми ожиданиями относительно уровня цен. Если ожидаемый уровень цен увеличивается с уровня P0
до уровня P1
, то номинальная зарплата будет зафиксирована на более высоком уровне w1
(w1
>w0
) и краткосрочная кривая совокупного предложения сдвинется вверх.
Мэнкью предложил в качестве причины положительной связи между уровнем цен и выпуском в краткосрочном периоде рассматривать вместо негибкой номинальной заработной платы негибкие цены. В качестве обоснования причины подобной негибкости было предложено рассматривать само изменение цен, как некий вид экономической деятельности, связанной с издержками. Издержки изменения цен принимают форму затрат на переиздание прайс-листов, каталогов, перепечатку ценников и т.д. Эти издержки в экономической литературе получили название «издержек меню». Мэнкью утверждал, что, принимая во внимание издержки изменения цен, фирмы, которые он считал монополистически конкурентными, могут найти выгодным и не всегда менять цены при изменении спроса. Он показал, что потери фирм от неизменности цен могут быть намного меньше, чем потери общества при наличии монопольной власти. Таким образом, даже при небольших издержках меню для потери фирм от неизменных цен могут оказаться ниже этих издержек и фирмы предпочтут не менять цены, хотя с точки зрения общества это влечет потери в благосостоянии. В результате вместо изменения цен фирмы реагируют посредством изменения выпуска. Если издержки меню для разных фирм различны, то одни сочтут выгодным изменить цены, а другие лишь изменят выпуск, и в результате мы будем наблюдать рост выпуска и повышение цен.
Итак, в долгосрочном периоде независимо от рассматриваемой теории мы получаем вертикальную кривую совокупного предложения. Относительно краткосрочного периода взгляды кейнсианцев и классиков были диаметрально противоположны: если первые, опираясь на негибкость цен, считали кривую совокупного предложения горизонтальной, то последние, напротив, считали, что в каждый момент времени рынок труда уравновешивается, и в результате получали вертикальную кривую предложения, как и для долгосрочной перспективы.
Современные взгляды на поведение совокупного предложения в краткосрочном периоде не столь противоречивы. Согласно как неоклассической, так и неокейнсианской теориям в краткосрочном периоде имеет место положительная зависимость между уровнем цен и выпуском, однако аргументы, объясняющие эту зависимость у этих теорий разные.
Кривая совокупного спроса (AD) показывает комбинации уровня цен и уровня выпуска, при которых рынки товаров и рынки активов одновременно находятся в равновесии. Ее легко получить из модели IS-LM.
Отрицательный наклон: повышение уровня цен ведет к сокращению реального предложения денег и порождает избыточный спрос на деньги или избыточное предложение облигаций. В результате цена облигаций падает, а значит ставка процента растет, что ведет к падению инвестиций и равновесного дохода.
На положение кривой AD влияют экзогенные параметры такие, как автономные расходы и номинальное предложение денег. Увеличение автономных расходов сдвигает кривую IS вправо, что ведет к росту выпуска при данном уровне цен и в результате кривая совокупного спроса также сдвигается вправо. Увеличение номинального предложения денег сдвигает вправо кривую LM, что в свою очередь приводит к сдвигу кривой совокупного спроса в том же направлении. Однако в данном случае, мы можем сказать точнее, каким именно образом будет сдвигаться кривая AD, если рассмотрим сдвиг вверх, то есть, изменение цен при данном уровне выпуска. Когда уровень цен растет, то кривая LM сдвигается вправо.
Для того чтобы выпуск остался неизменным нужно, чтобы кривая LM вернулась обратно. Это возможно, если цены вырастут в той же пропорции, что и номинальное предложение денег, тогда реальное предложение денег вернется к исходному уровню, и мы получим прежний выпуск при более высоком уровне цен.
Более того, если номинальное предложение денег увеличивается на x%, то и цены должны возрасти на x% при каждом уровне выпуска, что сдвигает кривую AD пропорционально вверх.
Итак, в основе денежно-кредитной политики лежит теория денег, изучающая, в том числе процесс воздействия денег и денежно-кредитной политики на состояние экономики в целом.
И современные кейнсианцы, и монетаристы признают, что изменение денежного предложения влияет на номинальный объем ВНП, но оценивают по-разному и значение этого влияния, и сам механизм: с точки зрения кейнсианцев, в основу денежно-кредитной политики должен быть положен определенный уровень процентной ставки, а с точки зрения монетаристов — само предложение денег.
Основные положения, отстаиваемые кейнсианцами в области теории денег, следующие:
1. Рыночная экономика представляет собой неустойчивую систему со многими внутренними «пороками». Поэтому государство должно регулярно использовать различные инструменты регулирования экономики, в том числе денежно-кредитные.
2. Цепочка причинно-следственных связей предложения денег и номинального ВНП такова: изменение денежного предложения является причиной изменения уровня процентной ставки, что, в свою очередь, приводит к изменению в инвестиционном спросе и через мультипликативный эффект — к изменению в номинальном ВНП.
3. Основное теоретическое уравнение, на котором базируется кейнсианство:
Y = C + G + I + NX
где Y — номинальный объем ВНП,
С — потребительские расходы,
G — государственные расходы на покупку товаров и услуг,
I — частные плановые инвестиции,
NX — чистый экспорт.
4. Кейнсианцы отмечают, что цель причинно-следственных связей между предложением денег и номинальным ВНП достаточно велика, а Центральный банк при проведении денежно-кредитной политики должен обладать значительным объемом экономической информации (например, о том, как скажется на инвестиционном спросе изменение процентной ставки и, соответственно, как изменится величина ВНП). Кроме того, между приростом денег в обращении, инвестициями и наполнением рынка товарами и услугами существует определенный временной лаг. И, наконец, наращивание денежного предложения при неизменном спросе может завести экономику, помимо прочего, в так называемую «ликвидную ловушку»: процентная ставка может снизиться до критического уровня, что будет означать исключительно высокое предпочтение ликвидности.
В самых общих чертах основные положения современного монетаризма таковы:
1. Монетаризм базируется на убеждении, что рыночная экономика — внутренне устойчивая система. Все негативные моменты — результат некомпетентного вмешательства государства в экономику, которое надо свести к минимуму.
2. Корреляция между, денежным фактором (массой денег в обращении) и номинальным объемом ВНП обнаруживается более тесная, чем между инвестициями и ВНП. Динамика ВНП следует непосредственно за динамикой денег. Монетаристы отмечают, что существует определенная взаимосвязь между количеством денег в обращении и общим объемом проданных товаров и услуг в рамках национальной экономики. Эта связь выражается уравнением обмена И.Фишера, или, иначе, уравнением количественной теории денег:
M·V=P·Q
где М — масса денег в обращении;
V — скорость обращения денег;
Р — средняя цена товаров и услуг,
Q — количество проданных товаров и оказанных услуг.
3. Сторонники количественной теории денег полагают, что вполне корректно сделать допущение о постоянстве скорости обращения денег. Такое допущение является абстракцией, поскольку показатель V, конечно, меняется, но очень незначительно, а существенные изменения могут быть обусловлены качественными преобразованиями в организации денежного обращения, что происходит нечасто и вполне предсказуемо.
4. Причинно-следственная связь между предложением денег и номинальным объемом ВНП осуществляется не через процентную ставку, а непосредственно. Тем самым известны как бы «входные и выходные данные» влияния предложения денег на ВНП, сам же механизм влияния денег скрыт.
5. Государство должно поддерживать обоснованный постоянный прирост денежной массы в обращении. Монетарное правило предполагает строго контролируемое увеличение денежной массы в обращении — в пределах 3—5% в год. Именно такой прирост денежной массы вызывает деловую активность в экономике. В случае неконтролируемого увеличения денежного предложения свыше 3—5% в год будет происходить раскручивание инфляции, а если темп вливаний в экономику будет ниже 3—5% годовых, то темп прироста ВНП будет падать.
Современные теоретические модели денежно-кредитной политики представляют собой синтез кейнсианства и монетаризма, в котором учтены рациональные моменты каждой из теорий. В долгосрочном периоде в денежно-кредитной политике сегодня преобладает монетаристский подход. Вместе с тем государство не отказывается в краткосрочном периоде от воздействия непосредственно на процентную ставку в целях быстрого экономического маневрирования.
Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания, так или иначе, определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции.
Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается, увеличение массы внесенных удобрений ведет к росту урожайности.
По направлению связи бывают прямыми,
когда зависимая переменная растет с увеличением факторного признака, и обратными,
при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными
и нелинейными.
В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем не линейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной.
Если изучаются более чем две переменные – множественной.
Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные сложные
связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые
и сильные
связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычисли тельных процедур, взаимодополнения при интерпретации результатов.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле, когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле, когда исследуется сила связи, и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.
Задачи собственно корреляционного анализа
сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа
лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы — параметрические — и принято называть корреляционными.
Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.
В данной работе теме корреляционного и регрессионного анализа посвящен вопрос № 2.
Вопрос № 2
Регрессия и корреляция
Условие задачи:
При проведении простой регрессионной модели для количества потребителей и площади размещенной рекламы (по размеру), используемой для привлечения потребителей, были получены следующие данные для шести рекламных стендов.
Площадь рекламного стенда (по размеру, в кв. метрах)
|
0.37
|
0.30
|
0.30
|
0.25
|
0.30
|
0.28
|
| Количество потребителей
|
240
|
150
|
182
|
95
|
210
|
125
|
2.1. Вычислите наименьшее равенство регрессии: y = a + bx.
2.2. Вычислите ожидаемое количество потребителей, если площадь рекламной вывески составляет 0.27 кв. метра.
2.3. Вычислите коэффициент корреляции для приведенных выше данных и прокомментируйте свой ответ.
Решение:
2.1 Вычислите уравнения регрессии
Для определения вида зависимости между количеством потребителей (y) и площадью рекламного стенда (х) построим корреляционное поле (scalter diagram) (рис. 1.).

Поскольку точки на корреляционном поле располагаются около некоторой прямой y = a + bx, то можно предположить наличие линейной регрессионной зависимости между переменными.
Для наглядности вычислений построим таблицу 1.
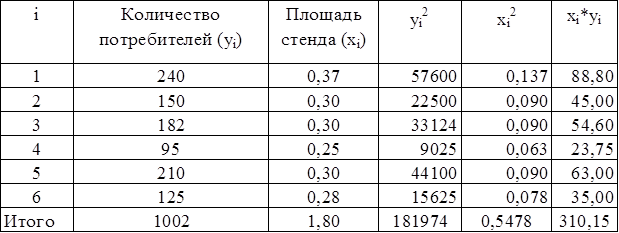
В соответствии с методом наименьших квадратов (МНК) коэффициенты уравнения линейной регрессии находятся по формулам:
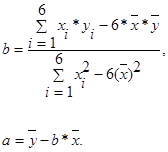
Для нашего примера имеем:
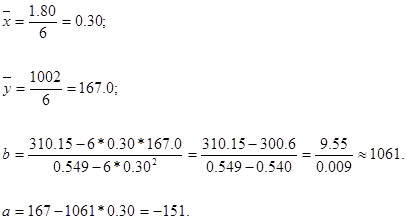
Таким образом, уравнение регрессии имеет вид:
Y = -151 + 1061Х.
При этом коэффициент в уравнении регрессии показывает, что увеличение площади рекламного стенда, например, на 0,01 кв. м. увеличивает количество потребителей приблизительно на 11 человек.
2.2 Вычислите ожидаемое количество потребителей, если площадь рекламной вывески составляет 0.27 кв. метра
Воспользовавшись уравнением линейной регрессии, получаем:
Y = -151 + 1061*0,27 ≈ 135 потребителей.
2.3 Вычислите коэффициент корреляции
Коэффициент корреляции вычисляется по следующей формуле:
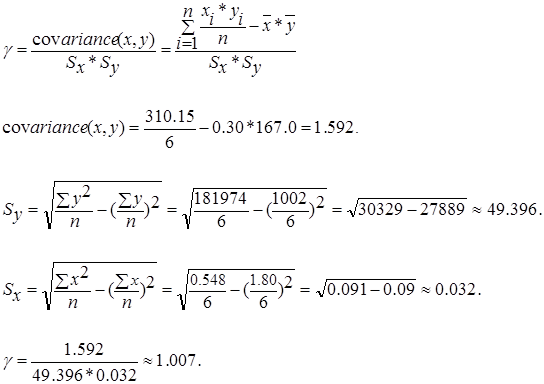
Для оценки значимости коэффициента корреляции на начальном этапе исследования можно пользоваться грубой оценкой:
При |γ| ≥ 0,70 имеется сильная линейная связь.
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. В частности, проверка качества отдельных видов продукции может быть связана с ее уничтожением (оценка крепости нити на разрыв, дегустация продуктов питания и т.п.); другие совокупности настолько велики, что было бы физически невозможно собрать данные в отношении каждого из их членов (например, при изучении пассажиропотоков или цен на рынках, исследованиях бюджетов семей). Выборочное наблюдение используют также для проверки результатов сплошного наблюдения.
Ту часть единиц, которые отобраны для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, – генеральной. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезен
тативна
(представительна).
Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо иной фактор, кроме случая.
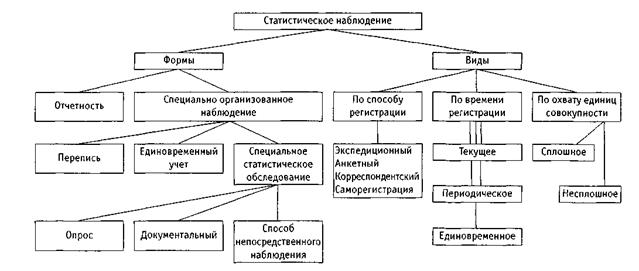
Рис.1. Формы, виды и способы статистического наблюдения
Существуют различные способы формирования выборочной совокупности. Это, во-первых, индивидуальный отбор, включающий такие разновидности, как собственно случайный, механический, стратифицированный, и, во-вторых, серийный, или гнездовой, отбор.
Собственно случайный отбор,
или случайная выборка, осуществляется с помощью жеребьевки либо по таблице случайных чисел. В первом случае всем элементам генеральной совокупности присваивается порядковый номер и на каждый элемент заводится жребий – пронумерованные шары или карточки-фишки, которые перемешиваются и помещаются в ящик, из которого затем отбираются наудачу. Во втором случае производится выбор случайных чисел (из специальных таблиц), которые образуют порядковые номера для отбора. Числа в таблицах обычно печатаются в виде блоков цифр (чтобы сделать таблицы более удобными для чтения по сравнению с не разбитой на блоки массой цифр), причем эти объединения в блоки не имеют статистического значения. Например, это могут быть числа:
5489, 5583, 3156, 0835,1988, 3912.
Применение комбинаций этих цифр зависит от размера совокупности: если в совокупности 1000 единиц, то порядковый номер каждой единицы должен состоять из трех цифр от 000 до 999. В таком случае приведенные выше случайные числа дали бы первые 8 номеров единиц выборочной совокупности:
548, 955, 833,156, 083, 519, 883, 912.
Дополнительные номера могут быть получены из последующих блоков тем же способом. Несколько сложнее выглядит процедура назначения номеров, отбираемых в выборочную совокупность, для случая произвольного объема генеральной. Теперь из случайных чисел таблиц формируется последовательность случайных величин, равномерно распределенных в интервале от 0 до 1. Могут использоваться и так называемые псевдослучайные числа, т.е. полученные по определенному алгоритму вручную или с помощью ПЭВМ. В нашем примере такими числами можно было бы считать:
0,5489, 0,5583, 0,3156, 0,0835; 0,1988, 0,3912 и т.д.
Предположим, что генеральная совокупность состоит из 7328 единиц. Тогда в выборочную совокупность должны войти единицы с номерами:
7328 х 0,5489 = 4022,3 или 4022;
7328 х 0,5583 = 4091,2 или 4091;
7328 х 0,3156 = 2312,7 или 2313;
7328x0,0835 = 611,9 или 612;
7328 х 0,1988 = 1456,8 или 1457;
7328 х 0,3912 = 2866,7 или 2867.
Процесс формирования случайных чисел и определения номера отбираемой единицы продолжается до тех пор, пока не будет получен заданный объем выборочной совокупности.
До настоящего времени на практике в качестве способа отбора обычно применяют механическое формирование выборочной совокупности, не связанное с процедурами получения случайных чисел. При этом способе отбирается каждый (n/N)-й элемент генеральной совокупности. Например, если имеется совокупность из 100 тыс. ед. и требуется выборка в 1000, то в нее попадет каждый сотый элемент. Если единицы в совокупности не ранжированы относительно изучаемого признака, то первый элемент выбирается наугад, произвольно, а если ранжированы, то из середины первой сотни. При достаточно большой совокупности этот способ отбора близок к собственно случайному, при условии, что применяемый список не составлен таким образом, чтобы какие-то единицы совокупности имели больше шансов попасть в выборку. К сожалению, это условие может нарушается. Так, использование 25%-й механической выборки при обследовании городского населения может привести к тому, что для каждого этажа при 4-квартирных площадках будет выбран один и тот же тип квартир (например, только трехкомнатные).
Отбор единиц из неоднородной совокупности осуществляется так называемым стратифицированным (расслоенным) способом, дающим модифицированную форму выборки. В этом случае генеральную совокупность предварительно разбивают на однородные группы с помощью типологической группировки, после чего производят отбор единиц из каждой группы в выборочную совокупность случайным или механическим способом. Этот метод гарантирует, что единицы разных групп (слоев) включаются в выборку пропорционально их численности в генеральной совокупности.
Особая форма составления выборки предполагает серийный, или гнездовой, отбор, при котором в порядке случайной или механической выборки выбирают не единицы, а определенные районы, серии (гнезда), внутри которых производится сплошное наблюдение.
Особенности обследуемых объектов определяют два метода отбора единиц в выборочную совокупность – повторный (отбор по схеме возвращенного шара) и бесповторный (отбор по схеме невозвращенного шара) При повторном отборе каждая попавшая в выборку единица или серия возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность всех единиц генеральной совокупности остается одинаковой. Бесповторный отбор означает, что каждая отобранная единица (или серия) не возвращается в генеральную совокупность и не может подвергнуться вторичной регистрации, а потому для остальных единиц вероятность попасть в выборку увеличивается.
Бесповторный отбор дает более точные результаты по сравнению с повторным, так как при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности. Поэтому он находит более широкое применение в статистической практике. И только в тех случаях, когда бесповторный отбор провести нельзя, используется повторная выборка (при обследовании потребительского спроса, пассажирооборота и т.п.).
В вопросе № 3 дается пример случайной выборки.
Вопрос № 3
Z-Тест
Условие задачи:
Булочная Truro отчиталась, что количество продаваемого ежедневно хлеба составляет 3000. Работник желает проверить точность данного отчета. Случайная выборка за 36 дней показала, что в среднем ежедневные продажи составляют 3150 с колебаниями в 300. Проверьте с 1% уровнем значимости, можно ли принять отчет булочной.
Решение:
1. Сформулируем нулевую и альтернативные гипотезы:
Н0
= {количество ежедневно продаваемого хлеба составляет}:μ = 3000.
Н1
= {количество ежедневно продаваемого хлеба не равно}:μ ≠ 3000.
2. Уровень значимости α = 0,01 (это вероятность отклонения верной гипотезы)
По таблице распределения Стьюдента при заданном уровне значимости α и числу степеней свободы df
, где df = n – 1 (n – объем выборки) находим квантили (критические точки)
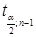 распределения Стьюдента. Они равны: распределения Стьюдента. Они равны:
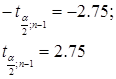
Accept H0
if -2.75 < Z < 2.75.
Reject H0
if Z ≤ -2.75; Z ≥ 2.75.
3. 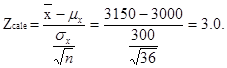
4. 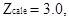 что свидетельствует о попадании в критическую область, то есть что свидетельствует о попадании в критическую область, то есть 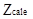 выпадает из зоны значений принятия гипотезы Н0
. выпадает из зоны значений принятия гипотезы Н0
.
5. Следовательно, гипотеза Н0
отвергается, то есть при 1% уровне значимости количество продаваемого ежедневно хлеба в количестве 3000 в виде отчета принята быть не может.
В качестве примеров распределений непрерывной случайной величины приведем следующие часто используемые в задачах управления качеством распределения, которые понадобятся нам для дальнейшей работы.
Нормальное (гауссовское) распределение имеет вид
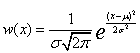 , , 
Здесь 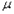 – среднее, – среднее, 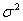 – дисперсия распределения СВ. – дисперсия распределения СВ.
Равномерное (равновероятное для дискретных СВ
) распределение на интервале [a,b] описывается соотношением
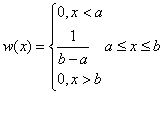
Среднее значение и дисперсия этого распределения равны соответственно
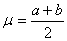 , , 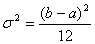 . .
Распределение 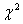 (хи – квадрат). Если (хи – квадрат). Если 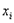 , , 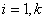 - независимые нормально распределенные числа с нулевым средним и единичной дисперсией, то статистика (функция случайных величин) - независимые нормально распределенные числа с нулевым средним и единичной дисперсией, то статистика (функция случайных величин)
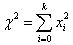 подчиняется распределению подчиняется распределению 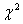 с k степенями свободы.
с k степенями свободы.
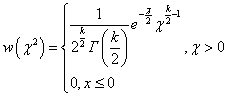
Здесь 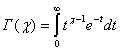 - гамма функция. Математическое ожидание и дисперсия данного распределения имеют вид соответственно - гамма функция. Математическое ожидание и дисперсия данного распределения имеют вид соответственно
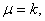 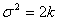 . .
Распределение Стьюдента (t - распределение).
Пусть z – нормальная случайная величина с нулевым математическим ожиданием и единичной дисперсией. Пусть также v – независимая от z СВ
, имеющая 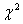 распределение с k степенями свободы. Тогда СВ
распределение с k степенями свободы. Тогда СВ
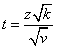
имеет t - распределение с k степенями свободы
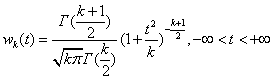
Среднее значение и дисперсия равны соответственно
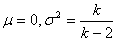 . .
Распределение Фишера-Снедекора.
Если u и v независимые СВ
, распределенные по закону 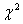 со степенями свободы
со степенями свободы  и и 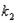 соответственно, то СВ соответственно, то СВ
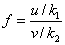
имеет распределение Фишера-Снедекора
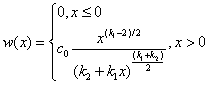
Здесь 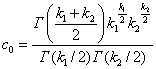 ., среднее значение и дисперсия равны соответственно ., среднее значение и дисперсия равны соответственно
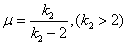 , , 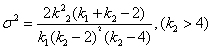 . .
Приведем примеры распределений дискретной СВ
, используемые в задачах управления качеством.
Гипергеометрическое распределение, часто применяемое в задачах выборочного контроля, имеет вид
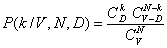
Здесь V - объем контролируемой партии, N – число изделий в выборке, k – число дефектных изделий в выборке, D – число дефектных изделий в партии,
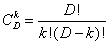 - число сочетаний из D по k. - число сочетаний из D по k.
Среднее значение и дисперсия этого распределения равны соответственно
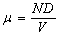 , , 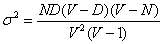 . .
В случае N<<V гипергеометрическое распределение хорошо аппроксимируется биномиальным распределением, вычисляемым по формуле

Здесь 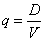 - вероятность дефекта, остальные обозначения соответствуют приведенным для гипергеометрического распределения. - вероятность дефекта, остальные обозначения соответствуют приведенным для гипергеометрического распределения.
Среднее значение и дисперсия для биномиального распределения вычисляются соответственно по формулам
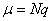 , , 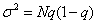 . .
В случае, если число испытаний N
возрастает, а вероятность q
уменьшается так, что Nq
= const, биномиальное распределение стремится к распределению Пуассона
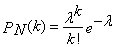 . .
Здесь N
– объем испытуемой выборки, k
– число интересующих исследователя событий, происшедших в процессе испытаний, 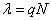 - среднее число событий в выборке (интенсивность потока событий). Среднее значение и дисперсия распределения Пуассона имеют вид - среднее число событий в выборке (интенсивность потока событий). Среднее значение и дисперсия распределения Пуассона имеют вид 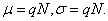
Вопросу распределения вероятности касаются вопросы № 4 и № 5.
Вопрос
№ 4
Chi-Squared Distribution
Условие задачи
Менеджер розничного магазина хочет установить, соотносится или нет количество покупателей, приходящих ежедневно в магазин со временем суток. Счетчик дает следующую информацию, касающуюся количества продаж в разное время дня.
| Период времени
|
Количество продаж
|
| 8.00 – 10.00
|
75
|
| 10.00 – 12.00
|
87
|
| 12.00 – 14.00
|
41
|
| 14.00 – 16.00
|
32
|
| 16.00 – 18.00
|
95
|
Если менеджер хочет проверить гипотезу, что продажи не соотносятся со временем суток на 5% уровне значимости, к какому выводу можно прийти.
Решение:
Сформулируем нулевую гипотезу:
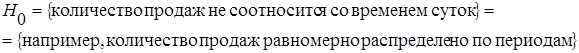
Пусть случайная величина Х – момент продажи. Тогда следующая формулировка нулевой гипотезы является эквивалентной:
Н0
= {случайная величина Х имеет равномерное распределение на [800
; 1800
]}; согласно равномерному закону, вероятность того, что случайная величина принадлежит одному из периодов равна:
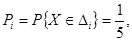 i = 1, …, 5, i = 1, …, 5,
где Δi
– длительность i-периода.
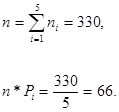
Расчетное значение статистики 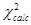 получаем по формуле: получаем по формуле:
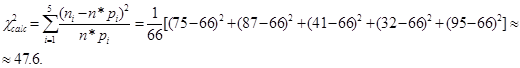
Табличное значение критерия при уровне значимости α = 0,05 и числе степеней свободы (k – 1) = (5-1) = 4 равно:
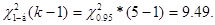
Так как 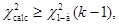 что гипотеза Н0
отвергается . что гипотеза Н0
отвергается .
Значит количество продаж в разные периоды времени за сутки действительно различное.
Вопрос № 5
Распределение вероятности
Условие задачи:
Существует 80% шанс, что обучаемый по программе в компании завершит программу успешно. Какова вероятность, что в группе из 4 выбранных случайным образом обучаемых:
5.1. Все четверо успешно завершат программу?
5.2. Максимум один обучающийся не справится с программой?
Решение:
В данной задаче имеем дело с числом Х появления события при 4 независимых опытах (обучаемые друг от друга независимы). Следовательно, дискретная случайная величина Х распределена по биномиальному закону, а ее возможные значения 0, 1, 2, 3, 4 соответствуют вероятностям:
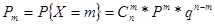
Где 0 < Р < 1; q = 1 – p, m = 1, …, n.
Данное распределение зависит от двух параметров: р и n (т.е. от р = 80%/100% = 4/5; n = 4).
Составим ряд распределения:
| Х:
|
0
|
1
|
2
|
3
|
4
|
| 1/625
|
16/625
|
192/625
|
256/625
|
256/625
|
Вероятность того, что никто не завершит успешно программу равна:
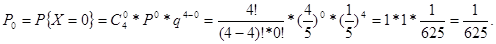
Вероятность того, что один человек завершит успешно программу равна:
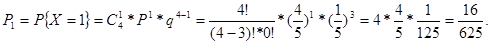
Вероятность того, что два человека завершат успешно программу равна:
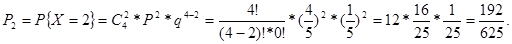
Вероятность того, что три человека завершат успешно программу равна:
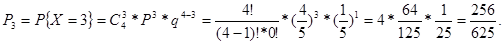
5.1. Вероятность того, что все четверо завершат успешно программу равна:

5.2. Вероятность того, что максимум один обучающийся не справится с программой, определяется следующим образом.
Для ответа на данный вопрос необходимо составить ряд распределения случайной величины Х – числа появлений противоположного события в 4 опытах.
| Х:
|
0
|
1
|
…
|
m
|
…
|
n
|
| Рn
|
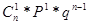
|
…
|
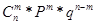
|
…
|
qn
|
При Х = 0: 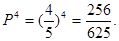
При Х = 1:  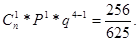
При Х = 2:  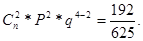
При Х = 3:  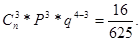
При Х = 4:  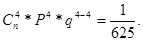
Вероятность того, что максимум один обучающийся не справится с программой равна 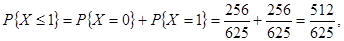 при этом математическое ожидание не справившихся с программой равно: при этом математическое ожидание не справившихся с программой равно:
Список литературы
1. Добрынин А.И., Салов А.И. Экономика. - М.: Юрайт, 2002.
2. Попов А.И. Экономическая теория. СПб.; М.; Харьков; Минск: Питер, 2000.
3. Фишер С., Дорнбут Р., Шмалензи Р. Экономика. - М.: Дело, 1993.
4. Экономическая теория. / Под ред. Видяпина В.И. и др. – М.: ИНФРА-М, 2000.
5. Экономическая теория. / Под ред. Камаева В.Д. – М.: ВЛАДОС, 1999.
|