| Министерство образования и науки
Российской федерации
Федеральное агентство по образованию
Новосибирский государственный университет
Механико-математический факультет
Кафедра математического моделирования
Дипломная работа
МИТКИНОВА Владимира Евгеньевича
Численный метод расчета нестационарных режимов гидравлических систем
Научный руководитель
Д. ф.-м. наук, профессор
А.Ф. Воеводин
Новосибирск 2010
Содержание
Содержание………………………………………………………………………..2
Введение…………………………………………………………………………...3
Постановка задачи………………………………………………………………...4
Математическая модель узла и условия сопряжения…………………………..7
Численный метод………………………………………………………………….9
Вычисление коэффициентов……………………………………………………12
Исследование свойств схемы…………………………………………………...13
Вычислительный эксперимент………………………………………………….15
Выводы…………………………………………………………………………...19
Литература……………………………………………………………………….20
Введение
Рассматривается математическая модель для расчета гидравлической системы на примере неустановившегося движения жидкости в системе трубопроводов. Результаты могут быть обобщены на любую гидравлическую систему (например, системы тепло-, водо-, нефте, и газоснабжения и т.п.).
Под гидравлической системой понимается совокупность участков труб произвольной трубопроводной системы и гидротехнических сооружений.
Движение жидкости в гидравлических системах описывается системой уравнений в частных производных гиперболического типа, причем область определения этих уравнений связана с ориентированным графом, отрезки (ребра) и вершины которого можно трактовать как различные элементы гидравлических систем.
Модель гидравлической системы представляется в виде композиции двух моделей: модели узла с сосредоточенными параметрами (т.е. все параметры функциями только времени), связываемой с вершинами графа. Модели трубы с распределенными параметрами (т.е. часть параметров являются функциями времени и пространственной координаты), связываемой с отрезками графа.
Для сопряжения этих двух моделей формулируются условия примыкания, выражающие связь между неизвестными на конце отрезка и параметрами в вершине, и балансовые соотношения, являющиеся функциональными связями между параметрами в вершине и неизвестными одновременно на всех отрезках, примыкающих к этой вершине.
Реклама

Постановка задачи
Уравнения, описывающие изотермические движение жидкости в трубах имеют вид [1,4]:
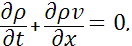
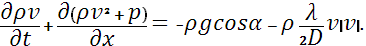
Здесь x-пространственная координата, t-время, ρ- плотность жидкости, g-ускорение силы тяжести, α-угол между осью канала и вектором силы тяжести. Последнее слагаемое во 2ом уравнение системы учитывает потери на трение жидкости о стенки канала, D-диаметр канала, λ-коэффициент трения.
Полагаем, что трение отсутствует, трубопровод горизонтальный, течение дозвуковое и жидкость слабо сжимаемая. Тогда исходная система перепишется в виде:
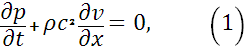
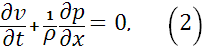
где 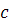 - скорость звука в жидкости. - скорость звука в жидкости.
Запишем систему в векторном виде:
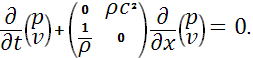
Решая характеристическое уравнение:
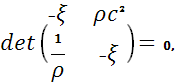
находим собственные значения 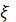 и характеристические направления нашей системы: и характеристические направления нашей системы:
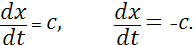
Заметим, что характеристики являются прямыми линиями, и их уравнения имеют вид:  . .
Также допускается запись системы (1), (2) в характеристической форме:
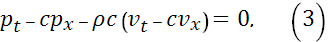

Определим инварианты Римана в виде:
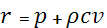
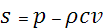
Учитывая (3) и (4), запишем систему уравнений гидроудара через инварианты:
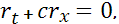
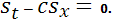
Система (1), (2) является гиперболической. Известно, что число граничных и начальных условий, задаваемых на границе области, равно числу характеристик, приходящих в область через эту границу, поэтому при  необходимо задавать два начальных условия: необходимо задавать два начальных условия:
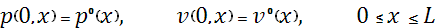
При 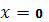 и и 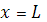 необходимо задавать по одному граничному условию, например: необходимо задавать по одному граничному условию, например:
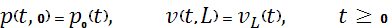
Для расчетов удобно систему уравнений (1), (2) представить в безразмерном виде. Пусть 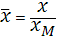 , , 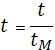 , , 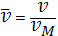 , , 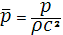 – безразмерные переменные, где – безразмерные переменные, где 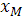 – масштаб длины, – масштаб длины, 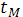 - масштаб времени, - масштаб времени, 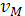 - масштаб скорости, - масштаб скорости, 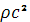 – масштаб давления. Тогда уравнения (1), (2) перепишутся в виде: – масштаб давления. Тогда уравнения (1), (2) перепишутся в виде:
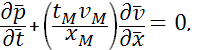
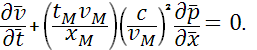
Выберем 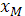 , , 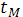 , , 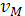 так, что так, что 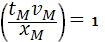 , и обозначим , и обозначим 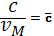 – безразмерная скорость звука. – безразмерная скорость звука.
В результате получим систему уравнений (1), (2) в безразмерной форме:
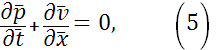
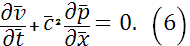
В дальнейшем для простоты выкладок черту над независимыми переменными и искомыми функциями будем опускать.
Математическая модель узла и условия сопряжения
Место соединения труб с дополнительным отводом (подводом) жидкости будем описывать моделью с сосредоточенными параметрами (моделью узла). При этом будем считать, что в узле:
а) происходит полное мгновенное перемешивание жидкости;
б) нет местных сопротивлений.
Пусть уравнения (1), (2) заданы на отрезках (ребрах) графа, содержащего J вершин и K отрезков; 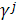 - множество номеров отрезков, примыкающих к j-ому узлу; - множество номеров отрезков, примыкающих к j-ому узлу; 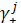 - множество номеров отрезков, из которых жидкость поступает в данный узел; - множество номеров отрезков, из которых жидкость поступает в данный узел; 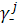 - множество номеров отрезков, которые отводят жидкость из узла. Тогда для j-го узла можно записать следующие балансовые соотношения, вытекающие из закона сохранения массы [1,2]: - множество номеров отрезков, которые отводят жидкость из узла. Тогда для j-го узла можно записать следующие балансовые соотношения, вытекающие из закона сохранения массы [1,2]:
Реклама

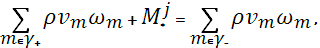
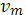 -скорость в концевом (начальном) сечении m-ой трубы. -скорость в концевом (начальном) сечении m-ой трубы.
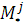 -сосредоточенный подвод (отвод) жидкости в узле. -сосредоточенный подвод (отвод) жидкости в узле.
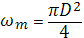 -площадь сечения m-ой трубы. -площадь сечения m-ой трубы.
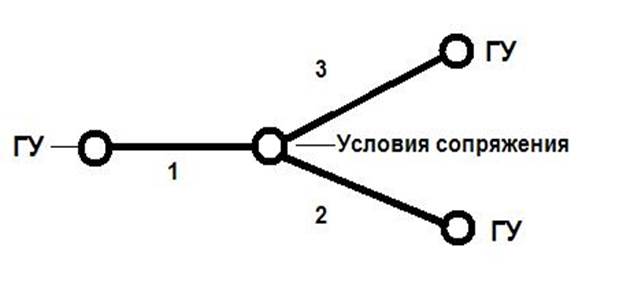
Рисунок 1
Для «стыковки» моделей трубы и узла сформулируем условия примыкания. Будем пренебрегать местными сопротивлениями вблизи узла по сравнению с гидравлическими сопротивлениями по длине труб. Тогда условия примыкания имеют вид:
 . .
Где 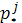 - сосредоточенный параметр в узле (узловое давление), - сосредоточенный параметр в узле (узловое давление), 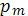 - давление в концевом (начальном) сечении m-й трубы. - давление в концевом (начальном) сечении m-й трубы.
В этом случае при заданных сосредоточенных параметрах условия примыкания обеспечивают единственность решения уравнений (1), (2) на отрезках, так как было отмечено, что для системы необходимо задавать по одному граничному условию на входных и выходных сечениях системы трубопровода.
Численный метод
Будем аппроксимировать систему (5), (6) схемой [2]:
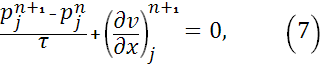
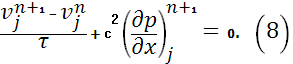
Выражаем из (7) 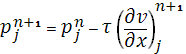 и подставляем в (8), получаем разностное уравнение: и подставляем в (8), получаем разностное уравнение:
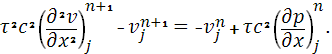
Это уравнение можно записать в виде:
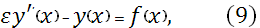
где: 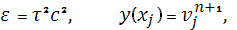
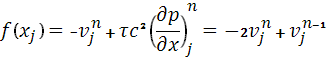 . .
Для решения уравнения (9) используем следующий способ дискретизации задачи [6].
Введем на отрезке [0,1] сетку с узлами 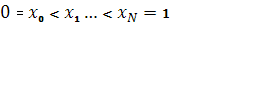 в общем случае с неравномерным шагом в общем случае с неравномерным шагом 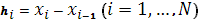 . .
Решение уравнения (9) будем искать например как решение задачи (преобразование Риккати)
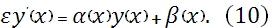
Тогда для прогоночных коэффициентов 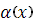 и и 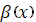 получим следующие уравнения: получим следующие уравнения:
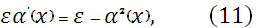
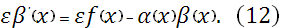
С учетом того, что начальные условия для прогоночных коэффициентов в узлах 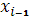 и и 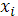 заранее неизвестны, вместо (10) рассматривается следующее уравнение для заранее неизвестны, вместо (10) рассматривается следующее уравнение для 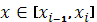 : :
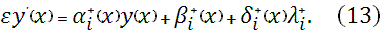
В отличии от уравнения (10) в (11) содержится дополнительное слагаемое, в котором 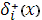 есть дополнительный прогоночный коэффициент, а параметр есть дополнительный прогоночный коэффициент, а параметр 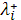 определяется как линейная комбинация значений определяется как линейная комбинация значений 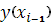 и и 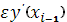 в виде: в виде:
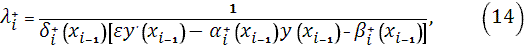
так, что (12) при 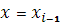 обращается в тождество. Тогда для вычисления прогоночных коэффициентов получаем следующие задачи обращается в тождество. Тогда для вычисления прогоночных коэффициентов получаем следующие задачи
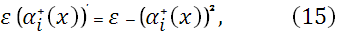
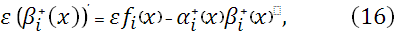
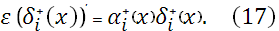
Отметим, что начальные значения для уравнений (15)-(17) 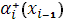 , , 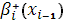 , , 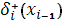 являются свободными параметрами и могут быть выбраны специальным образом с учетом свойств решения этих уравнений. являются свободными параметрами и могут быть выбраны специальным образом с учетом свойств решения этих уравнений.
Наряду с уравнением (13) на отрезке рассмотрим уравнение
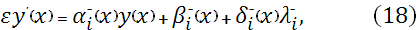
в котором прогоночные коэффициенты 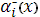 , ,  , , 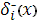 и параметр и параметр 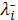 определяются аналогично предыдущему, но при задании начальных условий на правом конце отрезка, т.е. в точке определяются аналогично предыдущему, но при задании начальных условий на правом конце отрезка, т.е. в точке 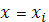 . В результате аналогично (14) получим . В результате аналогично (14) получим
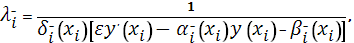
и, кроме того,
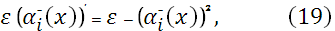
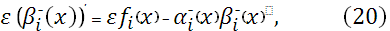
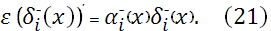
Тогда с помощью уравнения (13) при 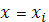 и уравнения (18) при и уравнения (18) при 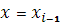 , полагая , полагая 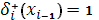 , , 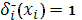 , , 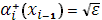 , , 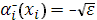 , , 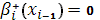 , , 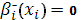 на каждом отрезке будем иметь систему двух уравнений: на каждом отрезке будем иметь систему двух уравнений:
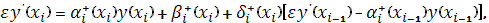
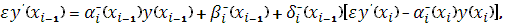
которые могут быть приведены к следующему виду
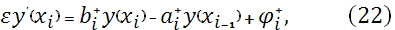
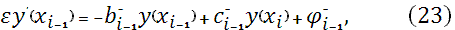
где
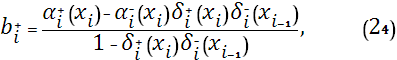
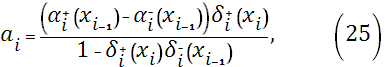
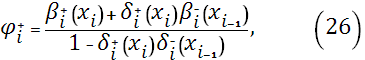
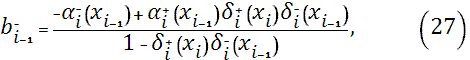
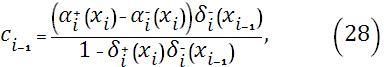
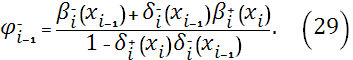
Приравнивая производные слева и справа, в узлах сетки 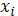 , из уравнения (22) на отрезке , из уравнения (22) на отрезке 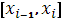 и уравнения (23) на отрезке и уравнения (23) на отрезке 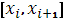 , получим разностные уравнения для неизвестных , получим разностные уравнения для неизвестных 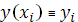 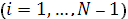
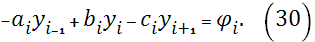
Здесь коэффициенты 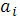 , , 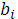 , , 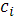 , , 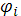 вычисляются по формулам (24)-(29), при этом: вычисляются по формулам (24)-(29), при этом:
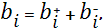
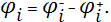
Для замыкания системы (30) привлекаем граничные условия.
Вычисление коэффициентов
Как было отмечено ранее граничные условия для уравнений (15)-(17), (19)-(21) являются свободными параметрами и могут быть выбраны специальным образом с учетом свойств решений этих уравнений.
Выбирая, для уравнений (15), (19) граничные условия: 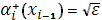 , , 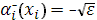 , для (16), (18) , для (16), (18)  , , 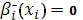 и для (17), (21) и для (17), (21) 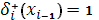 , , 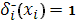 , в результате получаем: , в результате получаем:
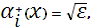
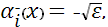
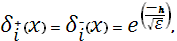
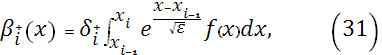
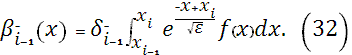
Для вычисления интегралов в значениях коэффициентов 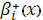 , , 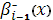 строим кубический сплайн Эрмита [7] для подынтегральной функции строим кубический сплайн Эрмита [7] для подынтегральной функции 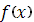 . При этом считается, что кроме значений функции . При этом считается, что кроме значений функции 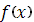 на концах отрезков задаются значения производных на концах отрезков задаются значения производных 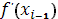 и и 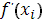 , которые вычислялись при помощи формул (22), (23). , которые вычислялись при помощи формул (22), (23).
Тогда интегралы в формулах (31), (32) вычисляются с локальной погрешностью 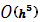 , и глобальная погрешность будет равняться , и глобальная погрешность будет равняться 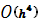 , что и подтверждается вычислительными экспериментами. , что и подтверждается вычислительными экспериментами.
Также для сравнения были проведены расчеты уравнений (31), (32) с помощью формулы трапеций.
Отметим, что коэффициенты системы (30) получаются в итоге постоянными величинами.
Исследования свойств схемы
Для исследования устойчивости метода прогонки и монотонности схемы используем принцип максимума, т.е. если в системе уравнений (30) 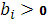 , , 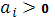 , , 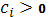 и и 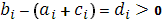 , то в матрице системы уравнений (30) присутствует диагональное преобладание, матрица является монотонной и выполняется оценка [6]. , то в матрице системы уравнений (30) присутствует диагональное преобладание, матрица является монотонной и выполняется оценка [6].
Рассмотрим коэффициенты системы уравнений (30):
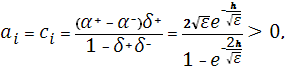
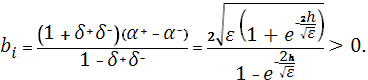
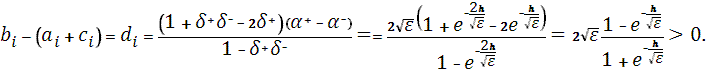
Отсюда следует, что схема является монотонной и метод прогонки устойчив.
Устойчивость по времени нетрудно показать с помощью спектрального признака устойчивости [5].
Перепишем уравнение (9) в следующей форме:
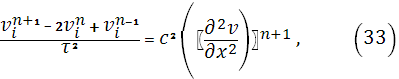
и решение (33) будем искать в виде: 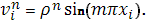 Тогда подставляя это выражение в (33) получим следующее уравнение: Тогда подставляя это выражение в (33) получим следующее уравнение:
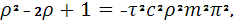
и следовательно,
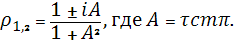
Очевидно, что
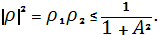
Отсюда следует, что схема абсолютно устойчива.
Для исследования порядка аппроксимации системы (5), (6) схемой (7), (8) разложим точное решение системы по формуле Тейлора в окрестности точки 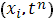 , предполагая наличие непрерывных вторых производных: , предполагая наличие непрерывных вторых производных:
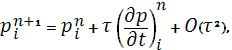
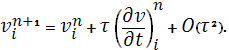
Подставляя эти значения в (7), (8) и, используя, свойства 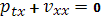 и и 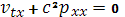 системы (5), (6) получим невязку: системы (5), (6) получим невязку:
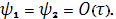
Таким образом, учтя погрешность при вычислении коэффициентов (31), (32) , система (5), (6) имеет аппроксимацию 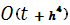 . .
Вычислительный эксперимент
Рассматривалась система трубопроводов, состоящая из 3 отрезков и 4 узлов. Длины всех отрезков одинаковы и равны 1, диаметры каналов одинаковы. Расчеты производились приведенным выше методом. Результаты расчетов сравнивались с точным решением системы (5), (6):
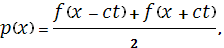
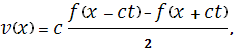
где 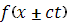 выбиралась: выбиралась:
1) 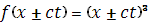 . .
Начальные условия: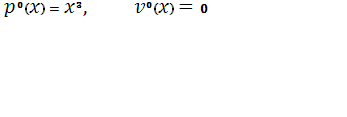 . .
Граничные условия: при 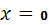 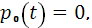
при 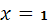 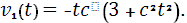
2) 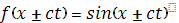 . .
Начальные условия:  . .
Граничные условия: при 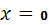 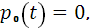
при 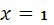 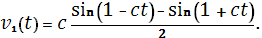
3) 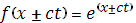 . .
Начальные условия: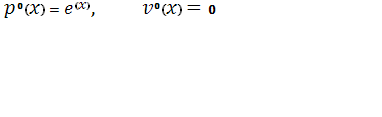 . .
Граничные условия: при 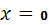 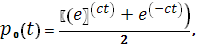
при 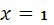 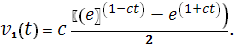
Таблицы погрешностей
Расчеты на момент времени 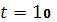 . .
1) Для первого случая:
| |
Сплайн Эрмита
|
Формула трапеций
|
| tau
|
h
|
Общая погрешность
|
Погрешность по h
|
Общая погрешность
|
Погрешность по h
|
| 0,1
|
0,1
|
0,832851872281
|
0,000005587977
|
0,883060158026
|
0,049862541589
|
| |
0,05
|
0,832846634174
|
0,000000349870
|
0,845471064588
|
0,012273448151
|
| |
0,025
|
0,832846305931
|
0,000000021627
|
0,836006949938
|
0,002809333501
|
| |
0,0125
|
0,832846285402
|
0,000000001098
|
0,833636730148
|
0,000439113711
|
| 0,05
|
0,1
|
0,411112170340
|
0,000014415426
|
0,555115166343
|
0,142993370234
|
| |
0,05
|
0,411098669010
|
0,000000914096
|
0,447750454263
|
0,035628658154
|
| |
0,025
|
0,411097811602
|
0,000000056688
|
0,420301941958
|
0,008180145849
|
| |
0,0125
|
0,411097757795
|
0,000000002881
|
0,413401372060
|
0,001279575951
|
| 0,025
|
0,1
|
0,201166720391
|
0,000030952418
|
0,635665878379
|
0,431272044005
|
| |
0,05
|
0,201137819976
|
0,000002052003
|
0,316227793596
|
0,111833959222
|
| |
0,025
|
0,201135896782
|
0,000000128809
|
0,230331588708
|
0,025937754334
|
| |
0,0125
|
0,201135774540
|
0,000000006567
|
0,208461455105
|
0,004067620731
|
2) Для второго случая:
| |
Сплайн Эрмита
|
Формула трапеций
|
| tau
|
h
|
Общая погрешность
|
Погрешность по h
|
Общая погрешность
|
Погрешность по h
|
| 0,1
|
0,1
|
0,0363862195882
|
0,0000003533755
|
0,0365225558362
|
0,0001361850555
|
| |
0,05
|
0,0363858866179
|
0,0000000204052
|
0,0364193116294
|
0,0000329408486
|
| |
0,025
|
0,0363858674276
|
0,0000000012149
|
0,0363940756462
|
0,0000077048655
|
| |
0,0125
|
0,0363858662825
|
0,0000000000698
|
0,0363878963462
|
0,0000015255654
|
| 0,05
|
0,1
|
0,0193290379468
|
0,0000003902564
|
0,0197702772371
|
0,0004398989059
|
| |
0,05
|
0,0193286704260
|
0,0000000227356
|
0,0194417061597
|
0,0001113278285
|
| |
0,025
|
0,0193286490606
|
0,0000000013702
|
0,0193567096123
|
0,0000263312812
|
| |
0,0125
|
0,0193286477694
|
0,0000000000790
|
0,0193356062043
|
0,0000052278731
|
| 0,025
|
0,1
|
0,0098628022883
|
0,0000008650402
|
0,0110834356765
|
0,0012156369665
|
| |
0,05
|
0,0098619896672
|
0,0000000524191
|
0,0102244373458
|
0,0003566386358
|
| |
0,025
|
0,0098619404102
|
0,0000000031621
|
0,0099557308589
|
0,0000879321489
|
| |
0,0125
|
0,0098619374304
|
0,0000000001824
|
0,0098854427220
|
0,0000176440120
|
3) Для третьего случая:
| |
Сплайн Эрмита
|
Формула трапеций
|
| tau
|
h
|
Общая погрешность
|
Погрешность по h
|
Общая погрешность
|
Погрешность по h
|
| 0,1
|
0,1
|
0,0503848043379
|
0,0000001782382
|
0,0505305705713
|
0,0001453810399
|
| |
0,05
|
0,0503846356429
|
0,0000000095432
|
0,0504215935780
|
0,0000364040466
|
| |
0,025
|
0,0503846266571
|
0,0000000005574
|
0,0503937716362
|
0,0000085821047
|
| |
0,0125
|
0,0503846261316
|
0,0000000000319
|
0,0503868920084
|
0,0000017024770
|
| 0,05
|
0,1
|
0,0276662900907
|
0,0000004434286
|
0,0284799145762
|
0,0008107561790
|
| |
0,05
|
0,0276658723062
|
0,0000000256441
|
0,0278803276463
|
0,0002111692492
|
| |
0,025
|
0,0276658481883
|
0,0000000015263
|
0,0277194379421
|
0,0000502795450
|
| |
0,0125
|
0,0276658467498
|
0,0000000000877
|
0,0276791571079
|
0,0000099987108
|
| 0,025
|
0,1
|
0,0143508893578
|
0,0000011533406
|
0,0175269261320
|
0,0031636285406
|
| |
0,05
|
0,0143498065190
|
0,0000000705018
|
0,0151730530598
|
0,0008097554684
|
| |
0,025
|
0,0143497402744
|
0,0000000042572
|
0,0145658072176
|
0,0002025096262
|
| |
0,0125
|
0,0143497362628
|
0,0000000002455
|
0,0144040736398
|
0,0000407760484
|
Замечание
1) Погрешность по 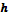 вычислялась путем, взятия разности, между общей погрешностью и погрешности по времени. Погрешностью по времени мы считаем общую погрешность при минимальном вычислялась путем, взятия разности, между общей погрешностью и погрешности по времени. Погрешностью по времени мы считаем общую погрешность при минимальном 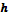 . .
2) С уменьшением шага 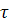 наблюдается увеличение погрешности по наблюдается увеличение погрешности по 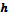 , это связано с зависимостью показателя диагонального преобладания , это связано с зависимостью показателя диагонального преобладания 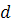 от шага от шага 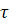 . .
Выводы
· В данной работе для решения начально-краевой задачи гиперболической системы дифференциальных уравнений была реализована схема с 4м порядком точности по пространственной переменной и 1м порядком по времени.
· Проведены исследования монотонности и устойчивости разностной схемы для линейной гиперболической системы второго порядка.
· Проведен сравнительный анализ численного и точного решения системы, подтверждающий теоретические выводы об устойчивости и точности схемы.
Литература
1. Воеводин А.Ф., Шугрин С.М. «Методы решения одномерных эволюционных систем». Новосибирск: Наука, 1993.
2. Воеводин А.Ф., Пономарев М.Ю. «Численный метод расчета нестационарных режимов гидравлических систем».
3. Годунов С.К. «Численное решение многомерных задач газовой динамики». Москва: Наука, 1976.
4. Меренков А.П. «Математическое моделирование и оптимизация систем тепло-, водо, нефте-, газоснабжения». Новосибирск: Наука, 1992.
5. Самарский А.А., Попов Ю.П. «Разностные схемы газовой динамики». Москва: Наука, 1975.
6. Воеводин А.Ф. «Метод факторизации для линейных и квазилинейных сингулярно возмущенных краевых задач для обыкновенных дифференциальных уравнений ». // Сиб. жур. вычисл. математики / РАН. Сиб. отд-ние.- Новосибирск, 2009.-Т. 12, №1.-с.1-15.
7. Волков Е.А. «Численные методы». Москва: Наука, 1987.
|