Определения
Графом 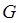 называется непустое конечное множество, состоящее из двух подмножеств называется непустое конечное множество, состоящее из двух подмножеств 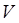 и и 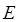 . Первое подмножество . Первое подмножество 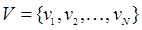 (вершины) состоит из любого множества элементов. Второе подмножество (вершины) состоит из любого множества элементов. Второе подмножество 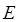 (дуги) состоит из упорядоченных пар элементов первого подмножества (дуги) состоит из упорядоченных пар элементов первого подмножества 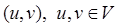 . Если вершины . Если вершины 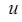 и и 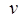 такие, что такие, что 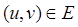 , то это вершины смежные. , то это вершины смежные.
Маршрутом в графе 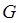 называется последовательность вершин называется последовательность вершин 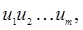 не обязательно попарно различных, где для любого не обязательно попарно различных, где для любого 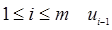 смежно с смежно с 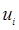 . Маршрут называется цепью, если все его ребра попарно различны. Если . Маршрут называется цепью, если все его ребра попарно различны. Если 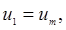 то маршрут называется замкнутым. Замкнутая цепь называется циклом. то маршрут называется замкнутым. Замкнутая цепь называется циклом.
Постановка задачи
Коммивояжер должен объездить n
городов. Для того чтобы сократить расходы, он хочет построить такой маршрут, чтобы объездить все города точно по одному разу и вернуться в исходный с минимумом затрат.
В терминах теории графов задачу можно сформулировать следующим образом. Задано n
вершин и матрица {c
ij
}, где c
ij
≥0 – длинна (или цена) дуги (i
, j
), 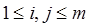 . Под маршрутом коммивояжера
z
будем понимать цикл i
1
, i
2
,…, i
n
,
i
1
точек 1,2,…, n. Таким образом, маршрут
является набором дуг. Если между городами i
и j
нет перехода, то в матрице ставится символ «бесконечность». Он обязательно ставится по диагонали, что означает запрет на возвращение в точку, через которую уже проходил маршрут коммивояжера
, длина маршрута l
(z
) равна сумме длин дуг, входящих в маршрут. Пусть Z
– множество всех возможных маршрутов. Начальная вершина i
1
– фиксирована. Требуется найти маршрут z0
ÎZ
, такой, что l
(z
0
)= minl
(z
), z
ÎZ
. . Под маршрутом коммивояжера
z
будем понимать цикл i
1
, i
2
,…, i
n
,
i
1
точек 1,2,…, n. Таким образом, маршрут
является набором дуг. Если между городами i
и j
нет перехода, то в матрице ставится символ «бесконечность». Он обязательно ставится по диагонали, что означает запрет на возвращение в точку, через которую уже проходил маршрут коммивояжера
, длина маршрута l
(z
) равна сумме длин дуг, входящих в маршрут. Пусть Z
– множество всех возможных маршрутов. Начальная вершина i
1
– фиксирована. Требуется найти маршрут z0
ÎZ
, такой, что l
(z
0
)= minl
(z
), z
ÎZ
.
Решение задачи
Основная идея метода ветвей и границ состоит в том, что вначале строят нижнюю границу φ длин множества маршрутов Z. Затем множество маршрутов разбивается на два подмножества таким образом, чтобы первое подмножество 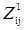 состояло из маршрутов, содержащих некоторую дугу (i, j), а другое подмножество состояло из маршрутов, содержащих некоторую дугу (i, j), а другое подмножество 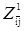 не содержало этой дуги. Для каждого из подмножеств определяются нижние границы по тому же правилу, что и для первоначального множества маршрутов. Полученные нижние границы подмножеств не содержало этой дуги. Для каждого из подмножеств определяются нижние границы по тому же правилу, что и для первоначального множества маршрутов. Полученные нижние границы подмножеств 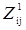 и и 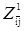 оказываются не меньше нижней границы множества всех маршрутов, т.е. φ(Z)≤ φ ( оказываются не меньше нижней границы множества всех маршрутов, т.е. φ(Z)≤ φ (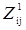 ), φ(Z) ≤ φ ( ), φ(Z) ≤ φ (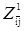 ). ).
Реклама

Сравнивая нижние границы φ
(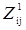 ) и φ
( ) и φ
(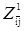 ), можно выделить то, подмножество маршрутов, которое с большей вероятностью содержит маршрут минимальной длины. ), можно выделить то, подмножество маршрутов, которое с большей вероятностью содержит маршрут минимальной длины.
Затем одно из подмножеств 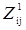 или или 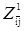 по аналогичному правилу разбивается на два новых по аналогичному правилу разбивается на два новых 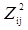 и и 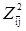 . Для них снова отыскиваются нижние границы φ
( . Для них снова отыскиваются нижние границы φ
(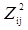 ), и φ
( ), и φ
(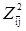 ) и т.д. Процесс ветвления продолжается до тех пор, пока не отыщется единственный маршрут. Его называют первым рекордом. Затем просматривают оборванные ветви. Если их нижние границы больше длины первого рекорда, то задача решена. Если же есть такие, для которых нижние границы меньше, чем длина первого рекорда, то подмножество с наименьшей нижней границей подвергается дальнейшему ветвлению, пока не убеждаются, что оно не содержит лучшего маршрута
. ) и т.д. Процесс ветвления продолжается до тех пор, пока не отыщется единственный маршрут. Его называют первым рекордом. Затем просматривают оборванные ветви. Если их нижние границы больше длины первого рекорда, то задача решена. Если же есть такие, для которых нижние границы меньше, чем длина первого рекорда, то подмножество с наименьшей нижней границей подвергается дальнейшему ветвлению, пока не убеждаются, что оно не содержит лучшего маршрута
.
Если же такой найдется, то анализ оборванных ветвей продолжается относительно нового значения длины маршрута. Его называют вторым рекордом. Процесс решения заканчивается, когда будут проанализированы все подмножества.
Для практической реализации метода ветвей и границ применительно к задаче коммивояжера укажем прием определения нижних границ подмножеств и разбиения множества маршрутов на подмножества (ветвление).
Для того чтобы найти нижнюю границу воспользуемся следующим соображением: если к элементам любого ряда матрицы задачи коммивояжера (строке или столбцу) прибавить или вычесть из них некоторое число, то от этого оптимальность плана не изменится. Длина же любого маршрутом коммивояжера
изменится на данную величину.
Вычтем из каждой строки число, равное минимальному элементу этой строки. Вычтем из каждого столбца число, равное минимальному элементу этого столбца. Полученная матрица называется приведенной по строкам и столбцам. Сумма всех вычтенных чисел называется константой приведения.
Константу приведения следует выбирать в качестве нижней границы длины маршрутов.
Разбиение множества маршрутов на подмножества
Для выделения претендентов на включение во множество дуг, по которым производится ветвление, рассмотрим в приведенной матрице все элементы, равные нулю. Найдем степени Θij
нулевых элементов этой матрицы. Степень нулевого элемента Θij
равна сумме минимального элемента в строке i
и минимального элемента в столбце j
(при выборе этих минимумов c
ij
– не учитывается). С наибольшей вероятностью искомому маршруту принадлежат дуги с максимальной степенью нуля.
Реклама

Для получения платежной матрицы маршрутов, включающей дугу (i
, j
) вычеркиваем в матрице строку i
и столбец j
, а чтобы не допустить образования цикла в маршруте, заменяем элемент, замыкающий текущую цепочку на бесконечность.
Множество маршрутов, не включающих дугу (i
, j
) получаем путем замены элемента c
ij
на бесконечность.
Пример решения задачи коммивояжера методом ветвей и границ
Коммивояжер должен объездить 6городов. Для того чтобы сократить расходы, он хочет построить такой маршрут, чтобы объездить все города точно по одному разу и вернуться в исходный с минимумом затрат. Исходный город A. Затраты на перемещение между городами заданы следующей матрицей:
| A |
B |
C |
D |
E |
F |
| A |
∞ |
26 |
42 |
15 |
29 |
25 |
| B |
7 |
∞ |
16 |
1 |
30 |
25 |
| C |
20 |
13 |
∞ |
35 |
5 |
0 |
| D |
21 |
16 |
25 |
∞ |
18 |
18 |
| E |
12 |
46 |
27 |
48 |
∞ |
5 |
| F |
23 |
5 |
5 |
9 |
5 |
∞ |
Решение задачи
Для удобства изложения везде ниже в платежной матрице заменим имена городов (A, B, …, F) номерами соответствующих строк и столбцов (1, 2, …, 6).
Найдем нижнюю границу длин множества всех маршрутов. Вычтем из каждой строки число, равное минимальному элементу этой строки, далее вычтем из каждого столбца число, равное минимальному элементу этого столбца, и таким образом приведем матрицу по строкам и столбцам. Минимумы по строкам: r1
=15, r2
=1, r3
=0, r4
=16, r5
=5, r6
=5.
После их вычитания по строкам получим:
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
11 |
27 |
0 |
14 |
10 |
| 2 |
6 |
∞ |
15 |
0 |
29 |
24 |
| 3 |
20 |
13 |
∞ |
35 |
5 |
0 |
| 4 |
5 |
0 |
9 |
∞ |
2 |
2 |
| 5 |
7 |
41 |
22 |
43 |
∞ |
0 |
| 6 |
18 |
0 |
0 |
4 |
0 |
∞ |
Минимумы по столбцам: h1
=5, h2
=h3
=h4
=h5
=h6
.
После их вычитания по столбцам получим приведенную матрицу:
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
11 |
27 |
0 |
14 |
10 |
| 2 |
1 |
∞ |
15 |
0 |
29 |
24 |
| 3 |
15 |
13 |
∞ |
35 |
5 |
0 |
| 4 |
0 |
0 |
9 |
∞ |
2 |
2 |
| 5 |
2 |
41 |
22 |
43 |
∞ |
0 |
| 6 |
13 |
0 |
0 |
4 |
0 |
∞ |
Найдем нижнюю границу φ
(Z
) = 15+1+0+16+5+5+5 = 47.
Для выделения претендентов на включение во множество дуг, по которым производится ветвление, найдем степени Θij
нулевых элементов этой матрицы (суммы минимумов по строке и столбцу). Θ14
= 10 + 0,
Θ24
= 1 + 0, Θ36
= 5+0, Θ41
= 0 + 1, Θ42
= 0 + 0, Θ56
= 2 + 0, Θ62
= 0 + 0,
Θ63
= 0 + 9, Θ65
= 0 + 2. Наибольшая степень Θ14
= 10. Ветвление проводим по дуге (1, 4).
Нижняя граница для множества 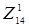 остается равной 47. Для всех маршрутов множества остается равной 47. Для всех маршрутов множества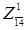 из города A мы не перемещаемся в город D. В матрице это обозначается выставлением в ячейку (1, 4) знака ∞. В этом случае выход из города A добавляет к оценке нижней границы по крайней мере наименьший элемент первой строки. φ
( из города A мы не перемещаемся в город D. В матрице это обозначается выставлением в ячейку (1, 4) знака ∞. В этом случае выход из города A добавляет к оценке нижней границы по крайней мере наименьший элемент первой строки. φ
(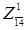 ) = 47 + 10. ) = 47 + 10.
В матрице, соответствующей 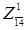 полагаем c
14
= ∞. полагаем c
14
= ∞.
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
11 |
27 |
∞ |
14 |
10 |
| 2 |
1 |
∞ |
15 |
0 |
29 |
24 |
| 3 |
15 |
13 |
∞ |
35 |
5 |
0 |
| 4 |
0 |
0 |
9 |
∞ |
2 |
2 |
| 5 |
2 |
41 |
22 |
43 |
∞ |
0 |
| 6 |
13 |
0 |
0 |
4 |
0 |
∞ |
После проведения процедуры приведения с r1
=10 получим новую нижнюю границу 57 + 10 = 67.
В матрице, соответствующей 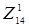 , вычеркиваем первую строку и четвертый столбец и положим c
41
= ∞, чтобы предотвратить появления цикла 1→ 4 → 1. Получим новую платежную матрицу {c
1
ij
}: , вычеркиваем первую строку и четвертый столбец и положим c
41
= ∞, чтобы предотвратить появления цикла 1→ 4 → 1. Получим новую платежную матрицу {c
1
ij
}:
| 1 |
2 |
3 |
5 |
6 |
| 2 |
1 |
∞ |
15 |
29 |
24 |
| 3 |
15 |
13 |
∞ |
5 |
0 |
| 4 |
∞ |
0 |
9 |
2 |
2 |
| 5 |
2 |
41 |
22 |
∞ |
0 |
| 6 |
13 |
0 |
0 |
0 |
∞ |
Для приведения надо вычесть минимум по первому столбцу: h1
=1. При этом нижняя граница станет равной 47+1 = 48. Сравнивая нижние границы
φ
(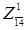 ) = 67 и φ
( ) = 67 и φ
(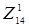 ) =48 < 67 выделяем подмножество маршрутов ) =48 < 67 выделяем подмножество маршрутов 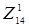 , которое с большей вероятностью содержит маршрут минимальной длины. , которое с большей вероятностью содержит маршрут минимальной длины.
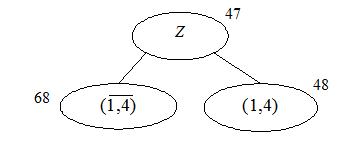
Рис. 1 Ветвление на первом шаге
Приведенная платежная матрица для 
| 1 |
2 |
3 |
5 |
6 |
| 2 |
0 |
∞ |
15 |
29 |
24 |
| 3 |
14 |
13 |
∞ |
5 |
0 |
| 4 |
∞ |
0 |
9 |
2 |
2 |
| 5 |
1 |
41 |
22 |
∞ |
0 |
| 6 |
12 |
0 |
0 |
0 |
∞ |
Далее продолжаем процесс ветвления. Найдем степени Θij
нулевых элементов этой матрицы Θ21
=16, Θ36
= 5, Θ42
= 2, Θ56
= 2, Θ62
= 0, Θ63
=9, Θ65
= 2. Наибольшая степень Θ21
. Затем множество  разбивается дуге (2, 1) на два новых разбивается дуге (2, 1) на два новых 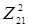 и и 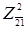 . .
В матрице для 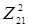 вычеркиваем строку 2 и столбец 1. дуги (1, 4) и (2, 1) образуют связный путь (2, 1, 4), положим c
42
= ∞, чтобы предотвратить появления цикла 2→1→ 4 → 2. вычеркиваем строку 2 и столбец 1. дуги (1, 4) и (2, 1) образуют связный путь (2, 1, 4), положим c
42
= ∞, чтобы предотвратить появления цикла 2→1→ 4 → 2.
| 2 |
3 |
5 |
6 |
| 3 |
13 |
∞ |
5 |
0 |
| 4 |
∞ |
9 |
2 |
2 |
| 5 |
41 |
22 |
∞ |
0 |
| 6 |
0 |
0 |
0 |
∞ |
Для приведения надо вычесть минимум по строке 4: r4
=2. При этом нижняя граница станет равной 48+2 = 50.
Нижняя граница для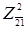 , полученная как на предыдущем шаге ветвления, равна 48 + 16 = 64. Сравнивая нижние границы φ
( , полученная как на предыдущем шаге ветвления, равна 48 + 16 = 64. Сравнивая нижние границы φ
(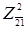 ) = 64 и φ
( ) = 64 и φ
(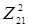 ) = 50 < 64 выбираем для дальнейшего разбиения подмножество маршрутов ) = 50 < 64 выбираем для дальнейшего разбиения подмножество маршрутов 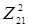 . .
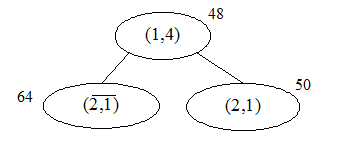
Рис. 2 Ветвление на втором шаге
Приведенная платежная матрица для 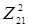
| 2 |
3 |
5 |
6 |
| 3 |
13 |
∞ |
5 |
0 |
| 4 |
∞ |
7 |
0 |
0 |
| 5 |
41 |
22 |
∞ |
0 |
| 6 |
0 |
0 |
0 |
∞ |
Степени Θij
нулевых элементов этой матрицы Θ36
= 5, Θ45
= 0, Θ56
= 22, Θ62
= 13, Θ63
=7, Θ65
= 0. Наибольшая степень Θ56.
Затем множество 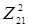 разбивается дуге (2, 1) на два новых разбивается дуге (2, 1) на два новых 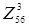 и и 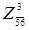 . .
Нижняя граница для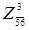 равна 50 + 22 = 72. В матрице для равна 50 + 22 = 72. В матрице для 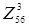 вычеркиваем строку 5 и столбец 6 и полагаем c
65
= ∞. Получим матрицу: вычеркиваем строку 5 и столбец 6 и полагаем c
65
= ∞. Получим матрицу:
| 2 |
3 |
5 |
| 3 |
13 |
∞ |
5 |
| 4 |
∞ |
7 |
0 |
| 6 |
0 |
0 |
∞ |
Для приведения надо вычесть минимум по строке 3: r3
=5. При этом нижняя граница станет равной 50+5 = 55. Выбираем для дальнейшего разбиения подмножество маршрутов 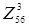 . .
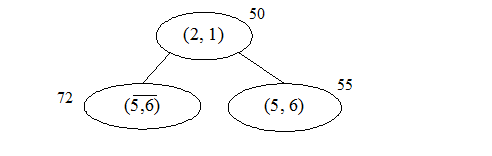
Рис. 3 Ветвление на третьем шаге
Приведенная платежная матрица для 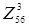
| 2 |
3 |
5 |
| 3 |
8 |
∞ |
0 |
| 4 |
∞ |
7 |
0 |
| 6 |
0 |
0 |
∞ |
Степени Θij
нулевых элементов этой матрицы Θ35
= 8, Θ45
= 7, Θ62
= 8, Θ63
=7. Выбираем Θ35
= 8. Разбиваем 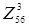 на на 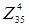 и и 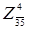 . .
Нижняя граница для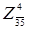 равна 55 + 8 = 64. В матрице для равна 55 + 8 = 64. В матрице для 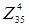 вычеркиваем строку 3 и столбец 5 и полагаем c
63
= ∞. Получим вычеркиваем строку 3 и столбец 5 и полагаем c
63
= ∞. Получим
Для приведения надо вычесть минимум по строке 4: r4=7. При этом нижняя граница станет равной 55+7 = 62. После приведения получим
Из матрицы 2´2 получаем два перехода с нулевой длинной: (4, 3) и (6, 2).
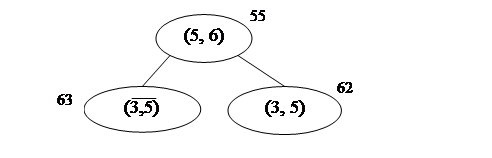
Рис. 4 Ветвление на четвертом шаге
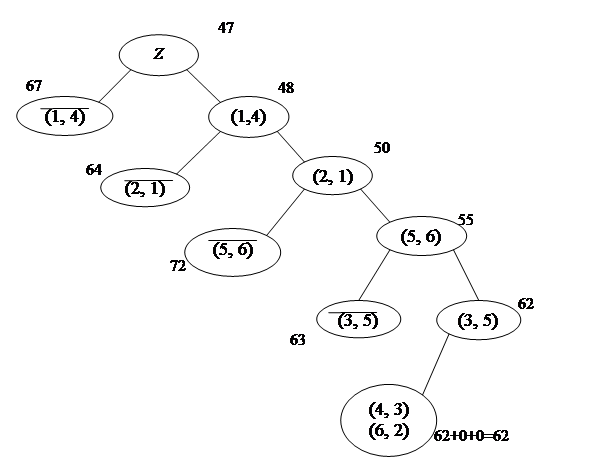
Рис. 5 Дерево ветвления с оценками
Полученный маршрутом коммивояжера
z
0
= (1, 4, 3, 5, 6, 2, 1) или (A-D-C-E-F-B-A).
|