|
Винтовые поверхности
Цилиндроид и Коноид
В разделе начертательной геометрии были рассмотрены наиболее распространенные в технике поверхности кругового цилиндра, кругового конуса, шара, прямой призмы, пирамиды. Эти поверхности являются не только наиболее распространенными, но и наиболее простыми по своему образованию. Наряду с такими поверхностями в технике применяются поверхности более сложного образования: цилиндроид, коноид, наклонный геликоид и винтовой цилиндр круглого нормального сечения. Для образования этих поверхностей в качестве направляющих часто используются винтовые линии. Поверхности, образованные с помощью винтовых линий, называют винтовыми поверхностями.
Цилиндроид. Поверхность цилиндроида образуется при перемещении прямой образующей линии 1 по двум кривым направляющим тип (рис. 298) при условии, что эта образующая все время остается параллельной некоторой заданной плоскости параллелизма σ (плоскость направления). Из комплексного чертежа видно, что образующие l, l1, l2, l3 параллельны плоскости параллелизма σ, так как их горизонтальные проекции l1, l2 и др. параллельны горизонтальной проекции χ горизонтально-проецирующей плоскости о. Цилиндроид подобного образования используется при конструировании и изготовлении отвалов плугов, в кузовостроении и при устройстве сводов.
Несколько иначе, с использованием винтовой линии, образуется поверхность винтового цилиндроида, применяющаяся при конструировании и изготовлении режущих инструментов (рис. 299).

Рис. 298. Цилиндроид
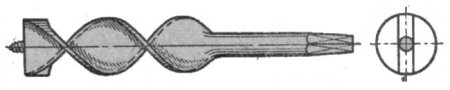
Рис. 299. Пример винтового цилиндроида — сверло по дереву
Коноид. Поверхность коноида образуется при перемещении образующей по двум направляющим, из которых одна — кривая, другая — прямая линия; образующая перемещается, оставаясь все время параллельной заданной плоскости параллелизма.
Для образования поверхности винтового коноида строят цилиндрическую винтовую линию 09 (рис. 300, а) и заставляют образующую перемещаться по этой винтовой и по ее оси так, чтобы она все время была параллельна горизонтальной плоскости (плоскости параллелизма). Если винтовой коноид рассечь цилиндром, имеющим с коноидом общую ось и меньший диаметр, то при пересечении получится винтовая линия того же шага. Часть поверхности, заключенной между винтовыми линиями, называется кольцевым коноидом (горизонтальная проекция имеет вид кольца). Любое сечение коноида плоскостью А—А, параллельной плоскости параллелизма, является прямой линией (прямая 10—11).
Реклама

Винтовой коноид применяют в прямоугольных резьбах (рис. 300, б). Для изображения винта строят ряд винтовых, линий различных диаметров (1 и 2 для большого диаметра d; 3 и 4 для малого — d1). На чертеже построен разрез винта горизонтальной плоскостью А—А. Изображенный винт — однозаходный. Винтовой коноид применяют также в транспортирующих устройствах (шнеки), при устройстве винтовых лестниц, въездов в многоэтажные гаражи (пандусы) и т. д
 . .
Рис. 300. Винтовой коноид и его применение
Винтовые поверхности
- Наклонный геликоид, Винтовой цилиндр круглого нормального сечения Машиностроительное черчение
Наклонный геликоид. Образование этой поверхности аналогично образованию винтового коноида: образующая перемещается по винтовой линии и по ее оси, оставаясь все время параллельной последовательным образующим, прямого кругового конуса (рис. 301, а). Если высоту направляющего конуса принять равной нулю, то наклонный геликоид превратится в винтовой коноид. Таким образом, винтовой коноид есть частный случай наклонного геликоида; образующие винтового коноида перпендикулярны к оси поверхности, в связи с чем эту поверхность иначе называют прямым геликоидом.
Наклонный геликоид так же, как и прямой, широко используется в резьбах. Для образования резьбы треугольного профиля (рис. 301, б) применяют два наклонных геликоида, имеющих обратный наклон образующих. По заданным диаметрам d и d1 и шагу h строят две винтовые линии; к их фронтальным проекциям проводят касательные прямые. Таким образом, изображение на плоскости П2 получается с закругленными углами. Для получения сечения горизонтальной плоскостью А—А проводят горизонтально-проецирующие плоскости. На чертеже проведена одна такая плоскость о. Точки, в которых эта плоскость пересекает винтовые линии, определяют треугольное сечение ABC. Пересечение треугольника А2В2С2 с линией сечения А—А позволяет определить точку Е2, а по ней — Е1 на горизонтальной проекции σ1 плоскости σ. Получившееся сечение винта ограничено двумя ветвями спирали Архимеда. В связи с последним наклонный геликоид иногда называют архимедовым геликоидом.
Реклама

Винтовой цилиндр круглого нормального сечения. Эта поверхность может быть образована двояко. В обоих случаях в качестве направляющей линии используется винтовая. По винтовой линии перемещается образующая окружность, причем центр ее скользит по винтовой, а плоскость окружности во все время движения остается перпендикулярной (нормальной) к винтовой. Для изображения поверхности более удобно пользоваться вторым способом образования поверхности с помощью шара, центр которого скользит по винтовой линии. Проекции перемещающегося шара изображаются на комплексном чертеже в виде ряда окружностей, касательно к которым должны быть проведены огибающие кривые (рис. 302). Оба способа образования поверхности винтового цилиндра известны, так как они аналогичны способам образования тора. На фронтальной проекции очерка поверхности, при известном соотношении радиуса винтовой линии, шага и радиуса образующей окружности появляются точки возврата А2, В2 и др., встречавшиеся ранее при изображении наклонно расположенного кругового кольца.
Поверхность винтового цилиндра круглого нормального сечения встречается в змеевиках и пружинах. Меридианное сечение поверхности представляет собой кривую, похожую на эллипс; в практике технического черчения ее условно заменяют окружностью.
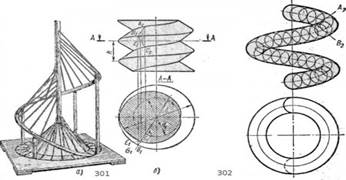
Рис. 301. Наклонный геликоид и его применение. Рис. 302. Пример винтового цилиндра — змеевик, пружина
Винтовые поверхности
На (фиг.366, а и б) показаны проекции винтовых поверхностей, образованных от движения отрезка, который своими концами перемещается по цилиндрической винтовой линии, находясь постоянно в плоскости, проходящей через ось вращения цилиндра (в плоскости меридионального сечения). Вид винтовой поверхности зависит от наклона отрезка по отношению к оси вращения цилиндра.

На (фиг.366, а) изображена винтовая поверхность, образованная отрезком, находящимся под углом 90° к оси вращения цилиндра, она называется прямой винтовой поверхностью, а на (фиг.366,б) - винтовая поверхность, образованная отрезком, находящимся под острым углом к оси, она называется косой винтовой поверхностью.
Обе эти винтовые поверхности можно встретить на винтах с упорной резьбой.
Винтовые линии, образованные точками А и В, соединены касательными прямыми условно, так как фактически они получаются пологими кривыми, приближающимися к прямым(фиг.366,б)
Винтовая поверхность
, поверхность, описываемая линией L, которая вращается с постоянной угловой скоростью вокруг неподвижной оси OO" и одновременно перемещается поступательно с постоянной скоростью вдоль этой оси (рис. 1). Винтовая поверхность, описываемая прямой, называется геликоидом (от греч. hélix, родительный падеж hélikos — спираль и éidos — вид). Если эта прямая пересекает ось OO" под прямым углом, то геликоид называется прямым (рис. 2). Прямой геликоид является минимальной поверхностью
. Любая Винтовая поверхность
может перемещаться по себе. Это свойство используется в технике (например, для устройства червячных передач). Винтовая поверхность
может быть посредством изгибания
наложена на поверхность вращения. В частности, прямой геликоид можно изогнуть Катеноид.
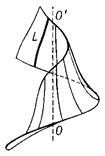 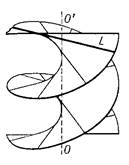
Рис. 1 к ст. Винтовая поверхность.
Рис. 2 Винтовая поверхность.
Минимальные поверхности
, поверхности, у которых средняя кривизна во всех точках равна нулю (см. Кривизна). Минимальные поверхности появляются при решении следующей вариационной задачи: в пространстве дана некоторая замкнутая кривая; среди всех возможных поверхностей, проходящих через эту кривую, найти такую, для которой часть её, заключённая внутри кривой, имела бы наименьшую площадь (минимальную площадь - отсюда название). Если заданная кривая - плоская, то решением, очевидно, будет ограниченный этой кривой кусок плоскости. В случае неплоской кривой необходимое условие, которому должна удовлетворять поверхность с минимальной площадью, было установлено Ж. Лагранжем в 1760 и несколько позже истолковано геометрически Ж. Мёнье в форме, эквивалентной требованию, чтобы средняя кривизна обращалась в нуль. Хотя это условие не является достаточным, т. е. не гарантирует минимума площади, однако впоследствии название «Минимальные поверхности» было сохранено за всякой поверхностью с нулевой средней кривизной. Если предположить поверхность заданной уравнением z = f (х, у), то, приравнивая нулю выражение для средней кривизны, приходят к дифференциальному уравнению с частными производными 2-го порядка:
(1 + q2)r - 2pqs + (1 + p2)t = 0,
где
Исследованием этого уравнения в различных формах занимались многие математики, начиная с Ж. Лагранжа и Г. Монжа. Примерами Минимальные поверхности могут служить: обыкновенная винтовая поверхность; катеноид - единственная (вещественная) Минимальные поверхности среди поверхностей вращения; «поверхность Шерка», определяемая уравнением
Минимальные поверхности
имеет во всех точках неположительную полную кривизну. Бельгийский физик Ж. Плато предложил способ экспериментального осуществления Минимальные поверхности при помощи мыльных плёнок, натянутых на проволочный каркаст. Винт
Изгибание (математическое), деформация поверхности, при которой длина каждой дуги любой линии, проведённой на этой поверхности, остаётся неизменной. Наглядный пример Изгибание - свёртывание листа бумаги в цилиндр или конус (при условии, что бумага нерастяжима; поэтому длина каждой дуги любой линии, проведённой на бумаге, остаётся неизменной). Напротив, раздувание шарика, изготовленного из тонкой резиновой плёнки, представляет собой пример деформации, которая не будет Изгибание
Изгибание поверхностей изучается в дифференциальной геометрии. Одна из теорем этой области - теорема Гаусса: при Изгибание поверхности произведение её главных кривизн (полная кривизна) в каждой точке остаётся неизменным. Из этой теоремы следует, что никакой кусок сферы при помощи Изгибание нельзя превратить в кусок сферы другого радиуса или придать ему плоскую форму. В современной дифференциальной геометрии особенно важное место занимают исследования возможности или невозможности Изгибание различных поверхностей. Доказано, что каждая замкнутая выпуклая поверхность (например, целая сфера, целый эллипсоид) не может изгибаться; если же из такой поверхности вырезать сколь угодно малый кусок, то оставшаяся часть будет допускать Изгибание Доказательство получено благодаря работам немецкого математика С. Кон-Фоссена и советских математиков А. Д. Александрова и А. В. Погорелова. Исследование Изгибание поверхности имеет важное значение для теории тонких оболочек в механике
Катеноид
(от лат. catema - цепь и греч. éidos - вид), поверхность, образуемая вращением цепной линии вокруг её оси; принадлежит к числу минимальных поверхностей. Форму Катеноид принимает мыльная плёнка (см. рис.), «натянутая» на 2 проволочных круга, плоскости которых перпендикулярны линии, соединяющей их центры.овая поверхность.на катеноид.

|