Міністерство освіти і науки України
Дніпропетровський Національний Університет
Дипломна робота
Оцінювання розподілу малої вибірки
Виконавець:
студентка групи МС-03-1
Яковенко В.В.
Дніпропетровськ
2008
Реферат
Дипломна робота: 65 сторінок, 10 джерел, 33 рисунки, 14 таблиць.
Перелік ключових слів: мала вибірка, обсяг вибірки, розподіл, відхилення емпіричної функції від гіпотетичної, емпірична функція розподілу, незміщена оцінка, спроможна оцінка.
Об’єкт дослідження: функція та щільність розподілу малої вибірки.
Мета роботи: порівняння класичного методу оцінювання розподілу вибірки, в основі якого лежить побудова емпіричної функції розподілу, з сучасними методами оцінювання розподілу малої вибірки.
Зміст
Вступ
1. Класичний метод оцінювання розподілу вибірки
1.1 Незміщені та спроможні оцінки
1.2 Емпірична функція розподілу
1.3 Моделювання неперервних випадкових величин
1.4 Критерій Смірнова
2. Сучасні методи оцінювання розподілу малої вибірки
2.1 Метод прямокутних внесків
2.2 Метод зменшення невизначеності
2.3 Метод апріорно-емпіричних функцій
3. Порівняння класичного методу та сучасних методів оцінювання розподілу малої вибірки
Висновки
Список використаних джерел
Вступ
Для математичної статистики проблема малої вибірки й досі залишається цікавою й актуальною. В сучасній науковій літературі відомості з цього питання різносторонні. Переважає умовний та суб'єктивний підхід. Деякі автори вважають малими вибірками вибірки обсягом до 200 спостережень, інші автори називають малими вибірками вибірки обсягом до 50 спостережень. Експериментально встановлено, що для знаходження стійких оцінок необхідна вибірка обсягом 40-50 спостережень. Вважається, що обсяг вибірки – 30 спостережень є граничним між малими та великими вибірками, оскільки для вибірок з обсягом менше 30 не можна застосовувати асимптотичні методи. Для дуже малих вибірок (обсягом 3-5 спостережень) практична цінність будь-якого висновку, знайденого класичними методами, незначна й для прийняття рішення необхідно використовувати інші методи (спеціально розроблені для вибірок малого обсягу [3]).
Малою вибіркою будемо називати вибірку, яку не можна проаналізувати методами, які базуються на групуванні вибіркових значень. З останнього випливає, що вибірку можна вважати великою, якщо при її обробці ми маємо можливість перейти до групування спостережень.
Реклама

Межу, яка відтинає великі й малі вибірки, не можна, звичайно, розуміти як точку в ряду дійсних цілих чисел. Достатні вибірки в силу випадковості вибору, утворюють деяку скінчену множину. З означення малої вибірки випливає необхідність індивідуального підходу до кожної окремої реалізації при обробці малої вибірки.
Важливою задачею математичної статистики є знаходження розподілу вибірки. Відомо багато класичних критеріїв для перевірки гіпотези про розподіл вибірки (наприклад, χ2
-критерій, критерій Колмогорова). Але для малої вибірки необхідні інші методи та підходи.
В дипломній роботі ставиться задача порівняння класичного методу оцінювання розподілу вибірки, в основі якого лежить побудова емпіричної функції розподілу, та сучасних методів оцінювання розподілу малої вибірки.
1. Класичний метод оцінювання розподілу вибірки
1.1 Незміщені та спроможні оцінки
Постановка задачі оцінювання параметрів розподілів. Нехай 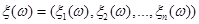 – реалізація вибірки – реалізація вибірки 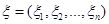 з розподілом з розподілом 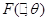 . Розподіл . Розподіл 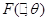 залежить від параметра залежить від параметра  , який набуває значень із множини , який набуває значень із множини  . Значення параметра . Значення параметра  в розподілі в розподілі 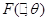 невідоме і його треба оцінити (визначити) за реалізацією невідоме і його треба оцінити (визначити) за реалізацією 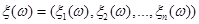 вибірки вибірки 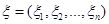 . У цьому полягає задача оцінювання параметрів розподілів. . У цьому полягає задача оцінювання параметрів розподілів.
Для оцінювання невідомого значення параметра  єдине, що нам відомо, та єдине, за допомогою чого ми можемо оцінювати (визначати) єдине, що нам відомо, та єдине, за допомогою чого ми можемо оцінювати (визначати)  , є реалізація вибірки , є реалізація вибірки 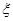 . Крім реалізації . Крім реалізації 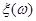 вибірки вибірки 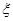 ми не маємо нічого, що надавало б якусь інформацію про значення параметра ми не маємо нічого, що надавало б якусь інформацію про значення параметра  . Тому оцінити (визначити) значення . Тому оцінити (визначити) значення  за реалізацією за реалізацією 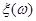 (точно чи хоча б наближено) означає, що реалізації (точно чи хоча б наближено) означає, що реалізації 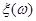 вибірки вибірки 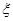 треба поставити у відповідність значення треба поставити у відповідність значення  . Точніше (формально) це означає, що для оцінювання . Точніше (формально) це означає, що для оцінювання  на вибірковому просторі – множині реалізації вибірок – необхідно визначити (побудувати, задати) функцію на вибірковому просторі – множині реалізації вибірок – необхідно визначити (побудувати, задати) функцію 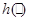 зі значеннями в зі значеннями в 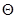 – множині можливих значень параметра – множині можливих значень параметра  - таку, що - таку, що
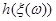 дорівнює дорівнює 
або хоча б
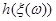 наближено дорівнює наближено дорівнює  . .
Значення  ми й будемо використовувати як ми й будемо використовувати як  . Слід зазначити, що для кожної реалізації . Слід зазначити, що для кожної реалізації 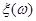 значення значення  , яке використовується як , яке використовується як  , буде своє; тому , буде своє; тому 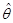 як функція як функція 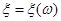 є випадковою величиною. є випадковою величиною.
Означення. Борелеву функцію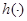 , задану на вибірковому просторі , задану на вибірковому просторі 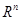 , зі значеннями в , зі значеннями в 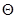 - множині можливих значень параметра - множині можливих значень параметра  - будемо називати статистикою, а - будемо називати статистикою, а 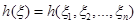 - борелеву функцію від вибірки зі значеннями в - борелеву функцію від вибірки зі значеннями в 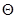 - оцінкою. - оцінкою.
Реклама

Будувати статистики 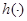 такі, щоб такі, щоб
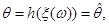 (1.1.1) (1.1.1)
тобто щоб за 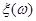 можна було точно визначити можна було точно визначити  , явно не вдається вже хоча б тому, що , явно не вдається вже хоча б тому, що  є константою, а оцінка є константою, а оцінка  як функція вибірки (функція випадкової величини) є випадковою величиною. Тому (хочемо ми того чи ні) для визначення як функція вибірки (функція випадкової величини) є випадковою величиною. Тому (хочемо ми того чи ні) для визначення  ми змушені задовольнятися значеннями ми змушені задовольнятися значеннями  , приймаючи (розглядаючи) їх за наближені значення , приймаючи (розглядаючи) їх за наближені значення  . Зазначимо, що для одного й того самого параметра . Зазначимо, що для одного й того самого параметра  можна запропонувати багато оцінок. можна запропонувати багато оцінок.
У зв’язку з постановкою задачі оцінювання параметрів розподілів як задачі одержання наближених значень  для для  треба вміти відповідати на запитання: наскільки великою є похибка треба вміти відповідати на запитання: наскільки великою є похибка 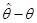 при заміні при заміні  на на 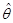 , інакше кажучи, як далеко можуть відхилятися значення оцінки , інакше кажучи, як далеко можуть відхилятися значення оцінки 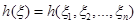 , обчисленої за вибіркою , обчисленої за вибіркою 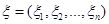 , від оцінюваної величини , від оцінюваної величини  ? ?
Кількісно міру похибки при заміні  на на 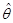 (міру розсіювання (міру розсіювання 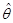 відносно відносно  ) будемо описувати величиною ) будемо описувати величиною
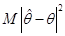 (1.1.2) (1.1.2)
Серед усіх оцінок з однією і тією самою дисперсією 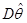 мінімальну міру розсіювання відносно мінімальну міру розсіювання відносно  мають оцінки, для яких мають оцінки, для яких 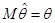 . Останнє випливає з нерівностей . Останнє випливає з нерівностей
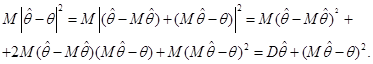 (1.1.3) (1.1.3)
Означення. Оцінку 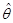 будемо називати незміщеною оцінкою параметра будемо називати незміщеною оцінкою параметра  , якщо , якщо
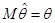 ,(1.1.4) ,(1.1.4)
або, що те саме, 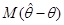 . .
Наочно незміщеність оцінки 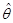 параметра параметра  можна трактувати так: при багаторазовому використанні оцінки можна трактувати так: при багаторазовому використанні оцінки 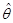 як значення як значення  , тобто при багаторазовій заміні , тобто при багаторазовій заміні  на на 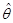 , середнє значення похибки , середнє значення похибки 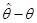 дорівнює нулеві. дорівнює нулеві.
Часто можна розглядати не одну оцінку 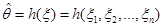 , побудовану за вибіркою , побудовану за вибіркою  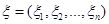 , а послідовність оцінок , а послідовність оцінок 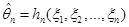 , , 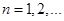 . У цій ситуації природно говорити про асимптотичну поведінку послідовності оцінок . У цій ситуації природно говорити про асимптотичну поведінку послідовності оцінок 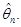
Означення. Послідовність оцінок 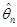 , , 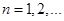 , будемо називати спроможною послідовністю оцінок параметра , будемо називати спроможною послідовністю оцінок параметра  , якщо для кожного , якщо для кожного 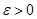
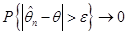 (1.1.5) (1.1.5)
при 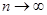 . .
Означення. Послідовність оцінок 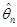 , , 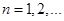 , будемо називати асимптотично незміщеною послідовністю оцінок параметра , будемо називати асимптотично незміщеною послідовністю оцінок параметра  , якщо , якщо
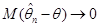 (1.1.6) (1.1.6)
або, що те саме, 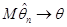 при при 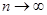 . .
1.2 Емпірична функція розподілу
Означення. Нехай 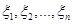 – вибірка з неперервного розподілу F. Функцію – вибірка з неперервного розподілу F. Функцію  , визначену на , визначену на  рівністю рівністю
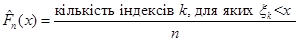 (1.2.1) (1.2.1)
будемо називати емпіричною функцією розподілу.  як функція випадкового вектора як функція випадкового вектора 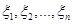 є випадковою величиною; тому є випадковою величиною; тому  також є функцією також є функцією 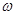 , тобто , тобто 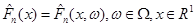 . .
Для кожного фіксованого х емпірична функція розподілу  є незміщеною та спроможною оцінкою значення функції розподілу є незміщеною та спроможною оцінкою значення функції розподілу 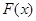 . .
Надалі буде зручно розглядати вибіркові значення 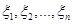 , розташовані в порядку зростання: , розташовані в порядку зростання: 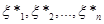 , тобто , тобто 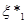 – найменше серед значень – найменше серед значень 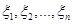 ; ; 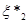 – друге за величиною і т. д.; – друге за величиною і т. д.; 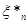 – найбільше з можливих значень – найбільше з можливих значень 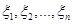 . .
Означення. Послідовність 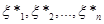 ,
будемо називати варіаційним рядом послідовності ,
будемо називати варіаційним рядом послідовності 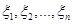 ,
а, ,
а, 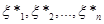 - порядковими статистиками. - порядковими статистиками.
У термінах порядкових статистик емпіричну функцію розподілу можна подати у вигляді
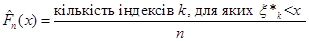 (1.2.2) (1.2.2)
Безпосередньо з рівності (1.2.2) знайдемо, що при фіксованому 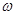 значення значення 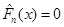 в кожній точці х відрізка в кожній точці х відрізка 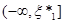 , оскільки кількість таких , оскільки кількість таких 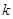 , для яких , для яких 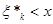 , дорівнює нулеві; , дорівнює нулеві; 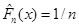 у кожній точці відрізка у кожній точці відрізка 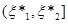 , тому що кількість тих , тому що кількість тих 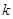 , при яких , при яких 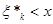 , дорівнює 1 і т. д.; нарешті, , дорівнює 1 і т. д.; нарешті, 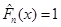 для кожного х з відрізка для кожного х з відрізка 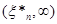 . .
Із вищенаведеного випливає, що для кожного фіксованого 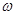 функція функція 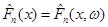 невід’ємна; вона є сталою на кожному з відрізків невід’ємна; вона є сталою на кожному з відрізків 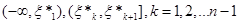 , , 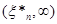 (а отже, неперервною зліва) і неспадною – зростає в точках (а отже, неперервною зліва) і неспадною – зростає в точках 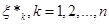 , стрибками , стрибками 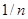 . .
Графік емпіричної функції розподілу  (точніше – реалізації (точніше – реалізації 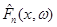 ) зображено на рис.1.2.1. ) зображено на рис.1.2.1.
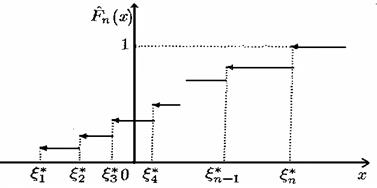
Рис.1.2.1. Графік реалізації емпіричної функції розподілу 
Зауваження 1. Для вибірок 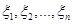 із неперервних розподілів імовірність збігу вибіркових значень дорівнює нулеві, але оскільки ми фіксуємо результати з заданою точністю (наприклад, до третього знака), деякі вибіркові значення можуть збігатися. При цьому стрибок емпіричної функції розподілу в точці із неперервних розподілів імовірність збігу вибіркових значень дорівнює нулеві, але оскільки ми фіксуємо результати з заданою точністю (наприклад, до третього знака), деякі вибіркові значення можуть збігатися. При цьому стрибок емпіричної функції розподілу в точці 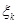 дорівнює дорівнює 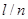 , де , де 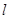 – кількість вибіркових значень, які збігаються з – кількість вибіркових значень, які збігаються з 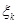 , враховуючи й , враховуючи й 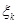 . .
Зауваження 2. Розподіл, що відповідає емпіричній функції розподілу  , будемо називати емпіричним. При кожному фіксованому , будемо називати емпіричним. При кожному фіксованому 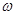 це дискретний розподіл, що ставить у відповідність кожній точці це дискретний розподіл, що ставить у відповідність кожній точці 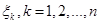 , "масу" , "масу" 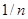 (або (або 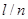 , якщо з , якщо з 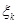 збігаються збігаються 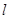 вибіркових значень, враховуючи й вибіркових значень, враховуючи й 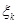 ) )
Про відхилення емпіричної функції розподілу  від функції розподілу від функції розподілу 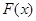 . .
Емпірична функція розподілу  є оцінкою функції розподілу є оцінкою функції розподілу 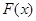 . Тому природно поставити запитання: наскільки емпірична функція розподілу . Тому природно поставити запитання: наскільки емпірична функція розподілу  , побудована за вибіркою , побудована за вибіркою 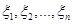 із F, відхиляється від із F, відхиляється від 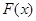 (якими можуть бути відхилення емпіричної функції розподілу (якими можуть бути відхилення емпіричної функції розподілу  від від 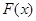 )? Зазначимо, що відхилення )? Зазначимо, що відхилення  від від 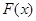 є випадковою величиною, і коли ми говоримо про таке відхилення, мусимо говорити про розподіл відхилення. є випадковою величиною, і коли ми говоримо про таке відхилення, мусимо говорити про розподіл відхилення.
Міру відхилення емпіричної функції розподілу  від функції розподілу від функції розподілу 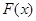 можна вводити різними способами. Розглянемо поки що відхилення емпіричної функції розподілу можна вводити різними способами. Розглянемо поки що відхилення емпіричної функції розподілу  від функції розподілу від функції розподілу 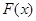 (коли остання неперервна), запропоноване А. М. Колмогоровим: (коли остання неперервна), запропоноване А. М. Колмогоровим:
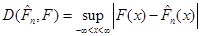 (1.2.3) (1.2.3)
(далі будемо писати 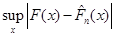 ). Ця міра відхилення має ту важливу властивість, що при досить великих ). Ця міра відхилення має ту важливу властивість, що при досить великих 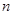 розподіл розподіл 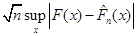 , незалежно від розподілу , незалежно від розподілу 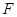 , з якого одержано вибірку , з якого одержано вибірку 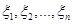 , близький до розподілу Колмогорова. , близький до розподілу Колмогорова.
Обчислення 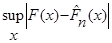 . Нехай . Нехай  – емпірична функція розподілу, побудована за вибіркою – емпірична функція розподілу, побудована за вибіркою 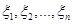 , точніше – за реалізацією вибірки; , точніше – за реалізацією вибірки; 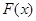 – неперервна функція розподілу. Часто виникає необхідність обчислити – неперервна функція розподілу. Часто виникає необхідність обчислити
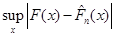 (1.2.4) (1.2.4)
для заданих  та та 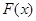 . Зазначимо, що . Зазначимо, що 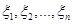 не обов’язково є вибіркою з розподілу не обов’язково є вибіркою з розподілу 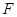 . .
Для того щоб обчислити
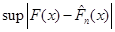 , ,
коли 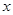 "перебігає" "перебігає"  , його досить обчислити на кожному з проміжків , його досить обчислити на кожному з проміжків
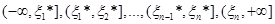 (1.2.5) (1.2.5)
й із знайдених чисел вибрати найбільше.
Обчислимо спочатку
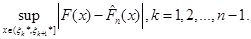 (1.2.6) (1.2.6)
Значення
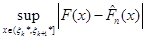 (1.2.7) (1.2.7)
дорівнює одному з чисел
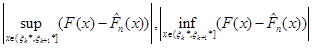 (1.2.8) (1.2.8)
Функція  стала на кожному з відрізків (1.2.5), стала на кожному з відрізків (1.2.5),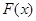 - неспадна функція; тому функція - неспадна функція; тому функція 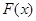 - - на відрізках (1.2.5) неспадна, й отже, (див. також рис.1.2.2) на відрізках (1.2.5) неспадна, й отже, (див. також рис.1.2.2)
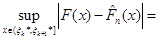
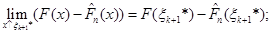 (1.2.9) (1.2.9)
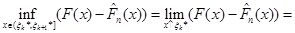
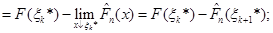 (1.2.10) (1.2.10)
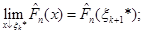 (1.2.11) (1.2.11)
(при обчисленні границь враховано, що  стала на проміжках (1.2.5) функція, а отже, неперервна зліва (див. також рис. 1.2.2). стала на проміжках (1.2.5) функція, а отже, неперервна зліва (див. також рис. 1.2.2).
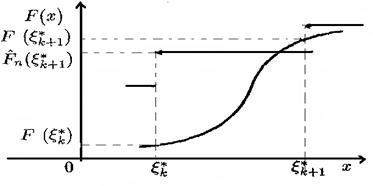
Рис.1.2.2. До обчислення 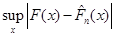
Отже,
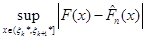
дорівнює
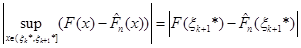 (1.2.12) (1.2.12)
або
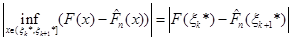 ,(1.2.13) ,(1.2.13)
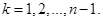
Для проміжків 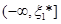 та та 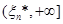 маємо маємо
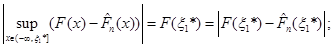 (1.2.14) (1.2.14)
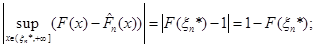 (1.2.15) (1.2.15)
Якщо через 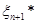 позначити довільну точку, що лежить праворуч від позначити довільну точку, що лежить праворуч від 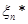 , то за означенням функції , то за означенням функції  її значення її значення 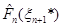 дорівнює 1 й останню рівність можна записати в тій самій формі, що й інші: дорівнює 1 й останню рівність можна записати в тій самій формі, що й інші:
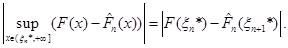 (1.2.16) (1.2.16)
Таким чином,
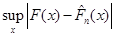
дорівнює найбільшому з чисел
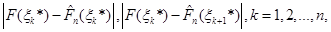 (1.2.17) (1.2.17)
де 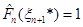 . .
1.3 Моделювання неперервних випадкових величин
Для розв’язання задач часто необхідно добути на ЕОМ послідовність вибіркових значень випадкової величини з заданим розподілом. Такий процес прийнято називати моделюванням випадкової величини. Випадкові величини зазвичай моделюються за допомогою перетворень одного або декількох незалежних значень рівномірно розподіленої на 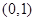 випадкової величини випадкової величини 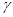 . .
Нехай випадкова величина 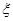 означена на інтервалі означена на інтервалі 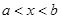 та має щільність та має щільність 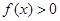 при при 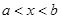 . Позначимо через . Позначимо через 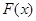 функцію розподілу функцію розподілу 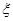 , яка при , яка при 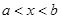 дорівнює дорівнює
 (1.3.1) (1.3.1)
Випадок 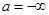 й (або) й (або) 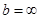 не виключається. не виключається.
Теорема 1.2.1. Випадкова величина 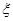 , яка задовольняє рівнянню , яка задовольняє рівнянню
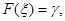 (1.3.2) (1.3.2)
має щільність розподілу 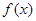 . .
Доведення. Оскільки функція 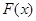 строго зростає в інтервалі строго зростає в інтервалі 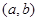 від від 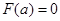 до до 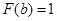 , тоді рівняння (1.3.2) має єдиний корень при кожному , тоді рівняння (1.3.2) має єдиний корень при кожному 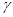 . При цьому . При цьому
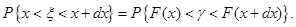 (1.3.3) (1.3.3)
Випадкова величина 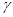 рівномірно розподілена в інтервалі рівномірно розподілена в інтервалі 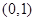 , тому , тому
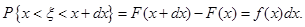 (1.3.4) (1.3.4)
Отже,
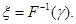 (1.3.5) (1.3.5)
Що і треба було довести.
1.4 Критерій Смірнова
Постановка задачі. Нехай 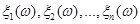 та та 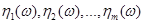 – реалізації вибірок – реалізації вибірок 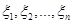 та та 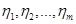 з неперервних розподілів з неперервних розподілів 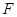 і і 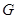 відповідно. Відносно невідомих розподілів відповідно. Відносно невідомих розподілів 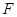 і і 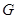 висувається гіпотеза висувається гіпотеза
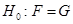 .(1.4.1) .(1.4.1)
Необхідно перевірити гіпотезу 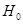 . .
Відхилення 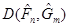 між емпіричними функціями розподілу між емпіричними функціями розподілу  та та 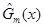 . Смірнов за відхилення між емпіричними функціями розподілу . Смірнов за відхилення між емпіричними функціями розподілу  та та 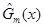 запропонував розглядати величину запропонував розглядати величину
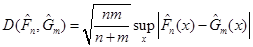 .(1.4.2) .(1.4.2)
Так введене відхилення задовольняє умовам, які забезпечують побудову критерію: 1) при справедливій гіпотезі 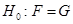 відхилення відхилення 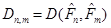 мінімально можливе в порівнянні зі значеннями мінімально можливе в порівнянні зі значеннями 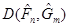 , коли , коли 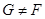 , оскільки , оскільки – незміщена та спроможна оцінка для – незміщена та спроможна оцінка для 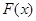 , , 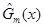 – незміщена та спроможна оцінка для – незміщена та спроможна оцінка для 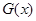 ; ;
2) при достатньо великих 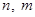 розподіл розподіл
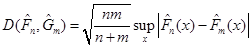 (1.4.3) (1.4.3)
мінімально можливого відхилення мало відрізняється від розподілу Колмогорова. Отже, за цей розподіл можна розглядати розподіл Колмогорова. Останнє випливає з теореми.
Теорема Смірнова. Нехай 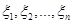 та та 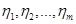 незалежні вибірки з неперервних розподілів незалежні вибірки з неперервних розподілів 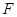 і і 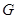 ; ;  та та 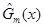 – емпіричні функції розподілів побудовані за вибірками – емпіричні функції розподілів побудовані за вибірками 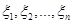 та та 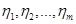 . .
Якщо 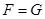 , тоді при , тоді при 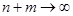 так, що відношення так, що відношення 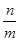 має границю, справедливо має границю, справедливо
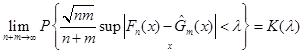 ,(1.4.4) ,(1.4.4)
де 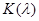 – функція розподілу Колмогорова. – функція розподілу Колмогорова.
Далі, обчислюємо відхилення (1.4.2) і порівнюємо його з мінімально можливим відхиленням 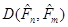 . При цьому, . При цьому, 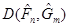 порівнюємо з порівнюємо з 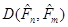 не безпосередньо (оскільки не безпосередньо (оскільки 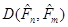 – випадкова величина), а порівнюємо з числом – випадкова величина), а порівнюємо з числом 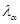 , що відокремлює малі значення , що відокремлює малі значення 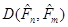 від великих. від великих.
Критерій Смірнова. Нехай 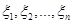 та та 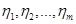 – незалежні вибірки з неперервних розподілів – незалежні вибірки з неперервних розподілів 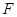 і і 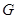 відповідно. відповідно. 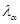 – верхня – верхня 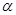 – границя розподілу Колмогорова. Якщо – границя розподілу Колмогорова. Якщо
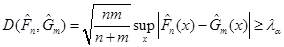 ,(1.4.5) ,(1.4.5)
то гіпотезу 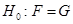 відхиляють, і не відхиляють в супротивному разі. відхиляють, і не відхиляють в супротивному разі.
Рівень значущості критерію – 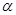 . .
Зауваження 1. 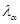 – верхня – верхня 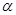 – границя розподілу Колмогорова визначається як розв’язок рівняння – границя розподілу Колмогорова визначається як розв’язок рівняння
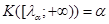 .(1.4.6) .(1.4.6)
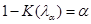 . .
2. Сучасні методи оцінювання розподілу малої вибірки
2.1 Метод прямокутних внесків (МПВ)
Метод прямокутних внесків був запропонований Чавчанідзе В.В. та Кумсішвілі В.А. в 1959 році [4]. Цей метод спрямований на побудову оцінки щільності розподілу f*(x).
Основні припущення метода такі. Множина можливих значень випадкових величин 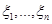 – відрізок [a,b]. Кожна випадкова величина використовується для побудови оцінки щільності окремо, при цьому кожна випадкова величина рівномірно "розмазується" в прямокутнику – відрізок [a,b]. Кожна випадкова величина використовується для побудови оцінки щільності окремо, при цьому кожна випадкова величина рівномірно "розмазується" в прямокутнику
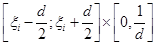 . .
За додаткову апріорну інформацію передбачається знання інтервалу [а;b], в якому випадкова величина 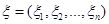 набуває значень. При цьому вважається, що щільність розподілу f(x) неперервна, не має дуже великих стрибків на заданому інтервалі й набуває значень. При цьому вважається, що щільність розподілу f(x) неперервна, не має дуже великих стрибків на заданому інтервалі й
f(x)≥0 при а≤x≤b;(2.1.1)
f(x)≡0 при x<a, x>b.(2.1.2)
Наявність подібної апріорної інформації, навіть за відсутності реалізацій 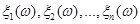 вибірки вибірки 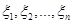 , дозволяє побудувати оцінку щільності f*(x). Жодній з можливих реалізацій , дозволяє побудувати оцінку щільності f*(x). Жодній з можливих реалізацій 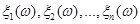 всередині інтервалу [а;b] не можна віддати перевагу. Саме таку особливість має рівномірний розподіл на [а;b] (див. рис 2.1.1) всередині інтервалу [а;b] не можна віддати перевагу. Саме таку особливість має рівномірний розподіл на [а;b] (див. рис 2.1.1)
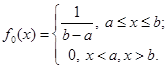 (2.1.3) (2.1.3)
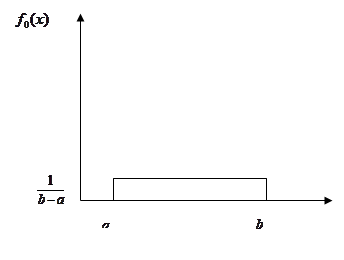
Рис. 2.1.1. Графік щільності рівномірного розподілу на [а;b]
Тому до проведення стохастичного експерименту оцінка щільності має вигляд
f*(x)= f0
(x).(2.1.4)
Функцію f0
(x) називатимемо апріорною щільністю розподілу.
Проводиться стохастичний експеримент, результатом якого є реалізація 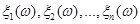 вибірки вибірки 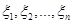 . Поява реалізацій . Поява реалізацій 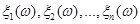 дає можливість уточнити оцінку (2.1.4). Останнє здійснюється шляхом індивідуального підходу до кожної окремої реалізації дає можливість уточнити оцінку (2.1.4). Останнє здійснюється шляхом індивідуального підходу до кожної окремої реалізації 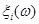 вибірки вибірки 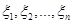 , при якому їй приписується елементарна рівномірна щільність на відрізку , при якому їй приписується елементарна рівномірна щільність на відрізку 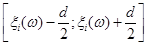 : :
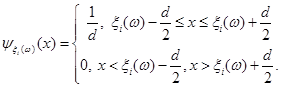 (2.1.5) (2.1.5)
Функцію 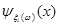 називають функцією внеску реалізації називають функцією внеску реалізації 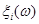 , при цьому d – ширина функції внеску, , при цьому d – ширина функції внеску, 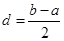 . .
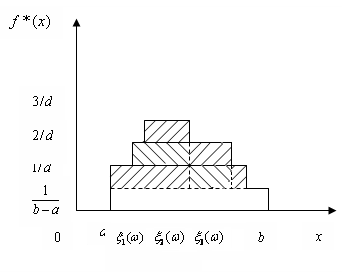
Функція внеску задається симетрично відносно точки 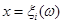 на інтервалі довжини d (див. рис. 2.1.2), отже, інформація про випадкову величину на інтервалі довжини d (див. рис. 2.1.2), отже, інформація про випадкову величину 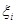 , одержана від реалізації , одержана від реалізації 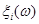 "розмазується". "розмазується".
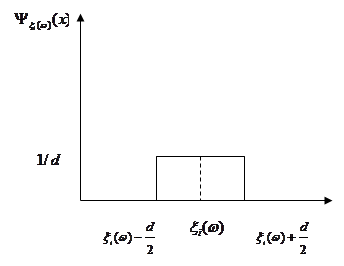
Рис. 2.1.2. Графік і-тої функції внеску
Тоді оцінка щільності 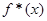 знаходиться підсумовуванням апріорної щільності знаходиться підсумовуванням апріорної щільності 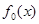 та всіх та всіх 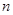 внесків реалізацій внесків реалізацій 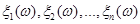 вибірки вибірки 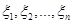 з однією й тією ж вагою з однією й тією ж вагою 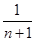 : :
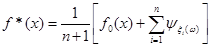 (2.1.6) (2.1.6)

Рис. 2.1.3. Графік оцінки щільності 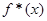
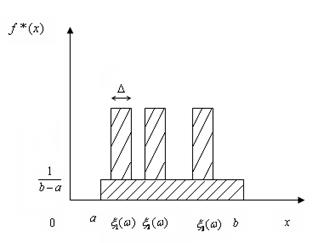
При побудові оцінки щільності МПВ за формулою (2.1.6) для внесків, що виходять за одну з меж інтервалу [а; b], рекомендується відкидати частини, що виходять за ці межі. Над частиною внеску, що знаходиться всередині інтервалу [а; b], як над основою, слід рівномірно надбудовувати прямокутник, площа якого дорівнює відкинутій.
Оцінка функції розподілу F*(x) для МПВ знайдена інтегруванням щільності f*(x)
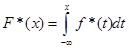 (2.1.7) (2.1.7)
2.2 Метод зменшення невизначеності (МЗН)
Метод зменшення невизначеності був запропонований Єременко В.І. та Свердликом А.Н. в 1963 році [5].
Цей метод дозволяє побудувати оцінку функції розподілу при апріорно відомому інтервалі [a,b], на якому вибірка 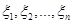 набуває значень. На відміну від МПВ, в якому інформація від реалізації набуває значень. На відміну від МПВ, в якому інформація від реалізації 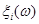 "розмазується" рівномірно на відрізку "розмазується" рівномірно на відрізку  , в МЗН пропонується "розподілити рівномірно стрибок імовірностей , в МЗН пропонується "розподілити рівномірно стрибок імовірностей 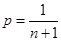 в точці в точці 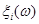 та розповсюдити вплив вказаного перетворення на весь відрізок та розповсюдити вплив вказаного перетворення на весь відрізок 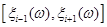 ". ".
Розглянемо рисунок 2.2.1, на якому за трьома реалізаціями 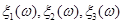 побудована оцінка F*(x). Для її знаходження необхідно на інтервалі [a,b] нанести на графік похилі лінії, число яких дорівнює (n+1)=4, під кутом побудована оцінка F*(x). Для її знаходження необхідно на інтервалі [a,b] нанести на графік похилі лінії, число яких дорівнює (n+1)=4, під кутом
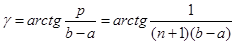 (2.2.1) (2.2.1)
до вісі абсцис на однаковій відстані одна від одної, яка дорівнює величині 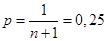 . Далі будується ламана лінія від точки (a;0) до точки (b;1) через середини відрізків, перпендикулярних вісі абсцис, що відновлені в точках . Далі будується ламана лінія від точки (a;0) до точки (b;1) через середини відрізків, перпендикулярних вісі абсцис, що відновлені в точках 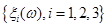 та замкнених між похилими лініями. Дана ламана лінія і є шуканою оцінкою F*(x). та замкнених між похилими лініями. Дана ламана лінія і є шуканою оцінкою F*(x).
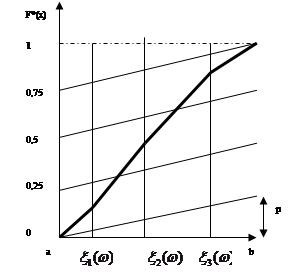
Рис. 2.2.1. Графік оцінки функції розподілу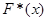
В загальному вигляді вираз для оцінки F*(x) на відрізку 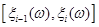 такий: такий:
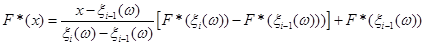 (2.2.2) (2.2.2)
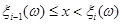
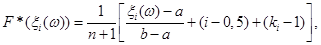 (2.2.3) (2.2.3)
де 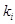 – число випадків збігу реалізацій – число випадків збігу реалізацій 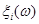 . .
МЗН є частинним випадком МПВ. Це легко перевірити. Для цього необхідно від оцінки функції розподілу F*(x) перейти до оцінки щільності f*(x). На рис. 2.2.2. зображена перша похідна від оцінки F*(x) за аргументом х, яка є нічим іншим, як оцінкою щільності f*(x). З рисунка 2.2.2, на якому цифри всередині прямокутників означають їх площі, видно, що f*(x) складається з:
1) апріорної рівномірної щільності 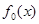 , яка займає 25% площі оцінки f*(x), та 2) трьох функцій внеску несиметричної форми, які займають по 25% площі оцінки f*(x). , яка займає 25% площі оцінки f*(x), та 2) трьох функцій внеску несиметричної форми, які займають по 25% площі оцінки f*(x).

Рис. 2.2.2. Графік оцінки щільності f*(x) розподілу
Аналітично функцію внеску реалізації 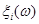 можна записати так: можна записати так:
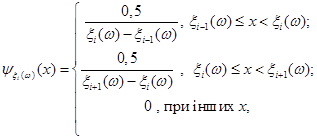 (2.2.4) (2.2.4)
де при 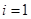 реалізація реалізація 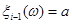 , а при , а при 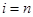 реалізація реалізація 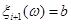 . .
Оцінка f*(x) знаходиться підсумовуванням всіх вказаних компонент 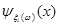 з вагами з вагами 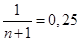 . Отже, вираз для МПВ визначає оцінку f*(x) для МЗН. Відміна лише в тому, що прямокутний внесок перетворений у внесок східчастої форми, що складається з двох прямокутників з рівною площею. . Отже, вираз для МПВ визначає оцінку f*(x) для МЗН. Відміна лише в тому, що прямокутний внесок перетворений у внесок східчастої форми, що складається з двох прямокутників з рівною площею.
Така заміна дозволяє досить легко будувати оцінку функції розподілу.
2.3 Метод апріорно-емпіричних функцій (АЕФ)
Метод апріорно-емпіричних функцій був запропонований Демковим І.П. та Потепун В.Е. в 1970 році [6].
Метод апріорно-емпіричних функцій дозволяє відразу отримати оцінку функції розподілу 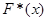 . .
Оцінка, побудована методом апріорно-емпіричних функцій, визначається так:
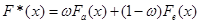 ,(2.3.1) ,(2.3.1)
де 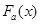 – апріорний розподіл, побудований за апріорними даними; – апріорний розподіл, побудований за апріорними даними;
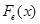 – емпіричний розподіл, побудований за вибіркою – емпіричний розподіл, побудований за вибіркою 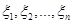 ; ;
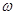 – коефіцієнт достовірності інформації про апріорний розподіл. – коефіцієнт достовірності інформації про апріорний розподіл.
З формули (2.3.1) випливає, що метод апріорно-емпіричних функцій також базується на використанні апріорної інформації, яка представляє собою інтервал [a,b], але при цьому їй приписується деяка вага 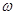 та передбачається, що та передбачається, що
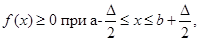 (2.3.2) (2.3.2)
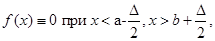 (2.3.3) (2.3.3)
де 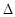 – інтервал дискретності, який визначається точністю спостереження (вимірювання) випадкової величини; – інтервал дискретності, який визначається точністю спостереження (вимірювання) випадкової величини; 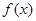 – щільність оцінюваної функції розподілу, яка є обмеженою функцією на – щільність оцінюваної функції розподілу, яка є обмеженою функцією на 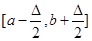 та має скінчене число точок розриву. Крім того, при побудові та має скінчене число точок розриву. Крім того, при побудові 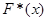 за допомогою метода апріорно- емпіричних функцій використовується індивідуальний підхід до кожної реалізації вибірки: інформація яка вкладена в реалізації за допомогою метода апріорно- емпіричних функцій використовується індивідуальний підхід до кожної реалізації вибірки: інформація яка вкладена в реалізації 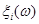 , розподіляється рівномірно на відрізку дискретності , розподіляється рівномірно на відрізку дискретності 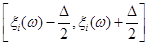 . .
Метод АЕФ передбачає наступний порядок дій для побудови оцінки функції розподілу.
1. Визначається відрізок [a,b] та відрізок дискретності 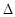 . За границі a та b, у випадку, якщо вони невідомі апріорно, рекомендується брати величини . За границі a та b, у випадку, якщо вони невідомі апріорно, рекомендується брати величини 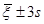 або або 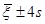 , де , де 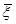 - середнє вибіркове для вибірки - середнє вибіркове для вибірки 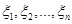 , , 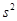 – вибіркова дисперсія, обчислена за вибіркою – вибіркова дисперсія, обчислена за вибіркою 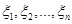 . Такий вибір меж відрізку базується на відомому в математичній статистиці "правилі . Такий вибір меж відрізку базується на відомому в математичній статистиці "правилі 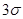 ". ".
2. Обчислюється відрізок означення функції 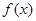 за умов (2.3.2), (2.3.3). за умов (2.3.2), (2.3.3).
3. Задається апріорна функція розподілу 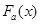 та будується на відрізку та будується на відрізку 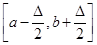 , при цьому , при цьому
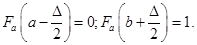 (2.3.4) (2.3.4)
4. Задається величина 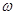 та будується на даному відрізку та будується на даному відрізку 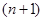 лінія обліку за формулою лінія обліку за формулою
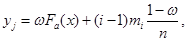 (2.3.5) (2.3.5)
де 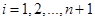 – номер лінії обліку; – номер лінії обліку; 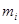 – число реалізацій, рівних за значенням до – число реалізацій, рівних за значенням до 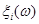 . .
5. В точках  відновлюються перпендикуляри до вісі абсцис та знаходяться точки перетину перпендикулярів: в точках відновлюються перпендикуляри до вісі абсцис та знаходяться точки перетину перпендикулярів: в точках 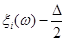 з і-ми лініями обліку, в точках з і-ми лініями обліку, в точках 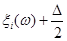 з (і+1)-ми лініями обліку. з (і+1)-ми лініями обліку.
6. Від точки 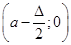 до точки до точки 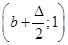 будується ламана лінія, яка з’єднує всі знайденні точки перетину, при цьому оскільки точки будується ламана лінія, яка з’єднує всі знайденні точки перетину, при цьому оскільки точки 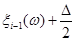 та та 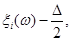 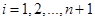 лежать на одній лінії обліку лежать на одній лінії обліку 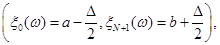 то ламана між цими точками йде за лініями обліку. Точки то ламана між цими точками йде за лініями обліку. Точки 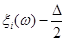 та та 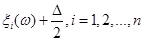 з’єднуються відрізком прямої. Знайдена ламана лінія є оцінкою функції розподілу. На рис. 2.3.1, як приклад наведено побудову з’єднуються відрізком прямої. Знайдена ламана лінія є оцінкою функції розподілу. На рис. 2.3.1, як приклад наведено побудову 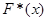 за вибіркою обсягом за вибіркою обсягом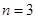 . .
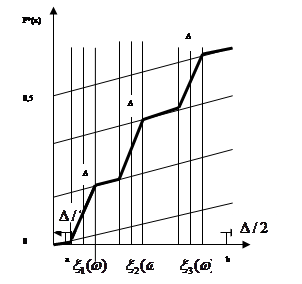
Рис. 2.3.1. Графік оцінки функції розподілу 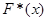
Методи АЕФ та МПВ, хоча й спрямовані на побудову оцінок різних функцій, відносяться до однієї групи методів, які базуються на використанні апріорної інформації, індивідуальному підході до реалізацій вибірок та "розмазуванні" інформації. Більш того, можна вважати, що метод АЕФ є теж методом прямокутних внесків. Розглянемо рисунок (2.3.2), де наведена оцінка щільності розподілу 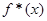 , побудована шляхом диференціювання , побудована шляхом диференціювання 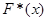 , що зображена на рис. 2.3.1, за змінною х. , що зображена на рис. 2.3.1, за змінною х.
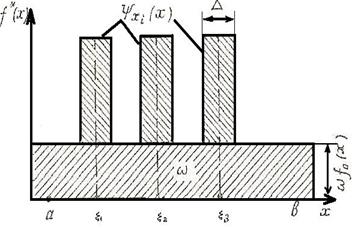
Рис. 2.3.2. Графік оцінки щільності розподілу 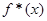
Оцінка 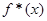 складається з лінійної суми апріорної рівномірної на відрізку складається з лінійної суми апріорної рівномірної на відрізку 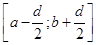 щільності щільності 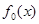 та прямокутних внесків та прямокутних внесків 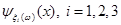 з відповідними вагами. Оцінка аналогічна до (2.1.6) в МПВ, але при цьому ширина внеску з відповідними вагами. Оцінка аналогічна до (2.1.6) в МПВ, але при цьому ширина внеску 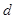 визначається тільки точністю вимірювальної апаратури визначається тільки точністю вимірювальної апаратури 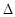 . В цьому істотна слабкість методу, оскільки зі зміною точності вимірювань (появи більш досконалого приладу) буде змінюватись ефективність оцінювання. . В цьому істотна слабкість методу, оскільки зі зміною точності вимірювань (появи більш досконалого приладу) буде змінюватись ефективність оцінювання.
Метод АЕФ має і сильну сторону. Відмова від прирівняння апріорної інформації та інформації, знайденої від окремої реалізації 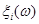 , та введення коефіцієнта достовірності інформації , та введення коефіцієнта достовірності інформації 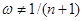 відрізняє метод АЕФ від МПВ та МЗН і є кроком вперед. Дійсно, апріорна інформація, яку має статистик, може мати різну природу, тому достовірність її може бути різною, а задання відрізняє метод АЕФ від МПВ та МЗН і є кроком вперед. Дійсно, апріорна інформація, яку має статистик, може мати різну природу, тому достовірність її може бути різною, а задання 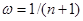 , як це зроблено в МПВ та МЗН, є обмеженням, яке знижує ефективність оцінювання розподілу вибірки. , як це зроблено в МПВ та МЗН, є обмеженням, яке знижує ефективність оцінювання розподілу вибірки.
3. Порівняння класичного методу та сучасних методів оцінювання малої вибірки
В дипломній роботі проведено експеримент, в якому кожен з розглянутих сучасних методів було порівняно з класичним методом.
Добувалась реалізація 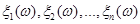 вибірки вибірки 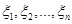 з відомого неперервного розподілу з відомого неперервного розподілу 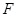 . Будувалась емпірична функція розподілу . Будувалась емпірична функція розподілу 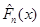 та оцінка функції розподілу та оцінка функції розподілу 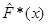 одним з трьох методів оцінювання функції розподілу малої вибірки. Далі обчислювалось колмогорівське відхилення емпіричної функції розподілу від гіпотетичної одним з трьох методів оцінювання функції розподілу малої вибірки. Далі обчислювалось колмогорівське відхилення емпіричної функції розподілу від гіпотетичної
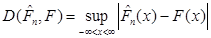 ,(3.1.1) ,(3.1.1)
а також відхилення побудоване аналогічно колмогорівському
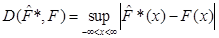 ,(3.1.2) ,(3.1.2)
в якому замість емпіричної функції розподілу береться оцінка функції розподілу 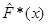 , обчислена одним з трьох методів (МПВ, МЗН, МАЕФ). , обчислена одним з трьох методів (МПВ, МЗН, МАЕФ).
Відхилення (3.1.1) та (3.1.2) порівнювались так: фіксувався обсяг вибірки n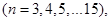 добувалось 20 реалізацій вибірки добувалось 20 реалізацій вибірки 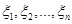 , обчислювалось 20 відхилень (3.1.1) та (3.1.2). Для класичного методу рахувалось середнє та дисперсія вибірок з 20 відхилень (3.1.1): , обчислювалось 20 відхилень (3.1.1) та (3.1.2). Для класичного методу рахувалось середнє та дисперсія вибірок з 20 відхилень (3.1.1):
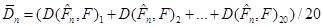 ;(3.1.3) ;(3.1.3)
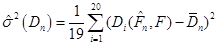 (3.1.4) (3.1.4)
Для методів оцінювання функції розподілу малої вибірки рахувалось середнє та дисперсія вибірок з 20 відхилень (3.1.2):
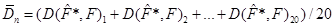 ;(3.1.5) ;(3.1.5)
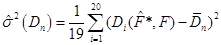 (3.1.6) (3.1.6)
Розглядались три розподіла 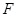 : рівномірний на проміжку [0,1], нормальний : рівномірний на проміжку [0,1], нормальний 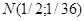 та експоненціальний з параметром та експоненціальний з параметром 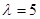 . .
В таблицях (3.1) – (3.9) наведено результати експериментів, які цілком очевидно свідчать на користь запропонованих методів оцінювання функції розподілу малої вибірки.
Метод прямокутних внесків
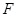 – рівномірний розподіл на [0;1] – рівномірний розподіл на [0;1]
Таблиця 3.1. Залежність величин 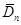 та та 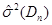 від обсягу вибіркиn від обсягу вибіркиn
Обсяг вибірки
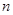
|
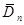 |
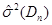 |
| Класичний метод |
Метод прямокутних внесків |
Класичний метод |
Метод прямокутних внесків |
| 3 |
0,456 |
0,166 |
0,023 |
0,008 |
| 4 |
0,436 |
0,166 |
0,013 |
0,008 |
| 5 |
0,351 |
0,129 |
0,009 |
0,006 |
| 6 |
0,316 |
0,118 |
0,007 |
0,002 |
| 7 |
0,319 |
0,141 |
0,013 |
0,007 |
| 8 |
0,275 |
0,116 |
0,006 |
0,004 |
| 9 |
0,269 |
0,114 |
0,007 |
0,003 |
| 10 |
0,251 |
0,111 |
0,008 |
0,003 |
| 11 |
0,240 |
0,111 |
0,003 |
0,001 |
| 12 |
0,201 |
0,103 |
0,003 |
0,003 |
| 13 |
0,191 |
0,096 |
0,002 |
0,001 |
| 14 |
0,229 |
0,097 |
0,003 |
0,001 |
| 15 |
0,195 |
0,093 |
0,004 |
0,002 |
За методом прямокутних внесків для рівномірного на [0;1] розподілу знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 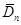 та та 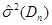 від обсягу вибірки n від обсягу вибірки n
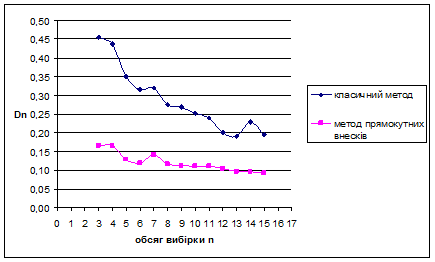
Рис. 3.1 Залежність величини 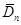 від обсягу вибірки n від обсягу вибірки n
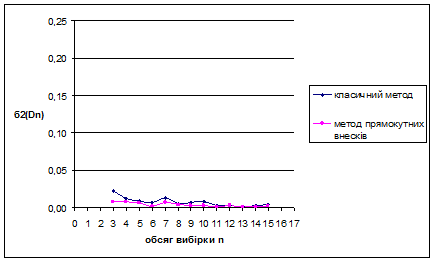
Рис. 3.2 Залежність величини 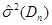 від обсягу вибірки n від обсягу вибірки n
Метод прямокутних внесків
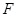 – нормальний розподіл N(1/2;1/36) – нормальний розподіл N(1/2;1/36)
Таблиця 3.2. Залежність величин 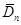 та та 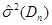 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
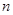
|
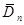 |
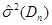 |
| Класичний метод |
Метод прямокутних внесків |
Класичний метод |
Метод прямокутних внесків |
| 3 |
0,455 |
0,355 |
0,024 |
0,002 |
| 4 |
0,414 |
0,351 |
0,016 |
0,003 |
| 5 |
0,361 |
0,323 |
0,013 |
0,005 |
| 6 |
0,333 |
0,331 |
0,008 |
0,003 |
| 7 |
0,303 |
0,369 |
0,011 |
0,002 |
| 8 |
0,295 |
0,344 |
0,004 |
0,010 |
| 9 |
0,270 |
0,374 |
0,000 |
0,007 |
| 10 |
0,253 |
0,363 |
0,001 |
0,007 |
| 11 |
0,254 |
0,397 |
0,009 |
0,016 |
| 12 |
0,216 |
0,374 |
0,004 |
0,000 |
| 13 |
0,245 |
0,378 |
0,006 |
0,000 |
| 14 |
0,209 |
0,378 |
0,004 |
0,000 |
| 15 |
0,207 |
0,373 |
0,004 |
0,000 |
За методом прямокутних внесків для нормального розподілу N(1/2;1/36) знайдено такі результати: метод виявився більш ефективним за класичний метод для вибірок обсягом менше ніж 6 спостережень. Для вибірок обсягом більше 6 спостережень метод не ефективний – це обумовлено тим, що за апріорну інформацію приймається рівномірний на [0;1] розподіл. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 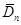 та та 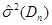 від обсягу вибірки n від обсягу вибірки n
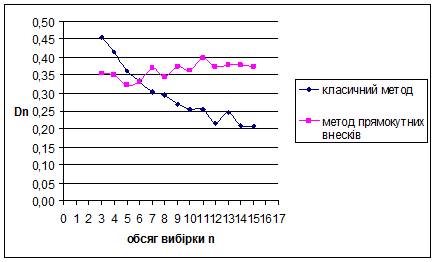
Рис. 3.3 Залежність величини 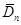 від обсягу вибірки n від обсягу вибірки n
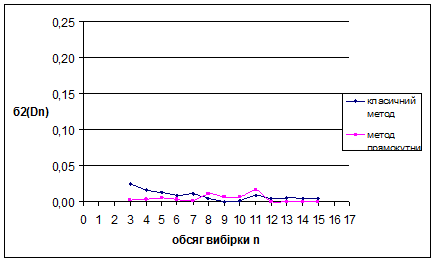
Рис. 3.4 Залежність величини 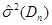 від обсягу вибірки n від обсягу вибірки n
Метод прямокутних внесків
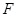 – експоненціальний розподіл з параметром λ=5 – експоненціальний розподіл з параметром λ=5
Таблиця 3.3. Залежність величин 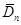 та та 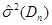 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
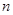
|
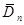 |
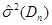 |
| Класичний метод |
Метод прямокутних внесків |
Класичний метод |
Метод прямокутних внесків |
| 3 |
0,460 |
0,299 |
0,015 |
0,006 |
| 4 |
0,400 |
0,305 |
0,010 |
0,003 |
| 5 |
0,320 |
0,279 |
0,009 |
0,003 |
| 6 |
0,287 |
0,273 |
0,008 |
0,002 |
| 7 |
0,288 |
0,273 |
0,006 |
0,002 |
| 8 |
0,283 |
0,273 |
0,010 |
0,002 |
| 9 |
0,281 |
0,270 |
0,009 |
0,003 |
| 10 |
0,280 |
0,267 |
0,005 |
0,002 |
| 11 |
0,244 |
0,282 |
0,003 |
0,001 |
| 12 |
0,222 |
0,283 |
0,003 |
0,001 |
| 13 |
0,221 |
0,280 |
0,004 |
0,001 |
| 14 |
0,201 |
0,269 |
0,002 |
0,001 |
| 15 |
0,191 |
0,266 |
0,002 |
0,001 |
За методом прямокутних внесків для експоненціального розподілу з параметром λ=5 знайдено такі результати: метод виявився більш ефективним за класичний метод для вибірок обсягом менше ніж 10 спостережень. Для вибірок обсягом більше 10 спостережень метод не ефективний – це обумовлено тим, що за апріорну інформацію приймається рівномірний на [0;1] розподіл. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 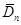 та та 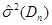 від обсягу вибірки n від обсягу вибірки n
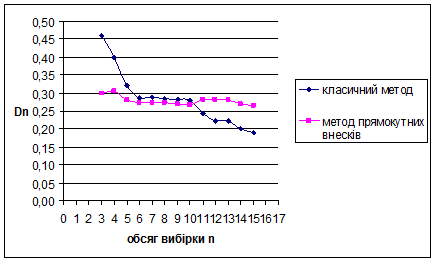
Рис. 3.5 Залежність величини 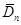 від обсягу вибірки n від обсягу вибірки n
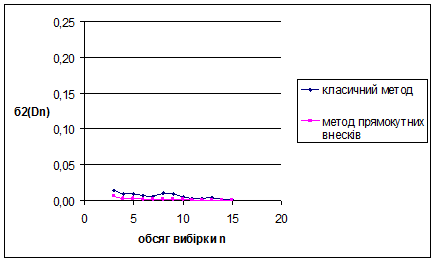
Рис. 3.6 Залежність величини 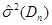 від обсягу вибірки n від обсягу вибірки n
Метод зменшення невизначеності
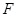 – рівномірний розподіл на [0;1] – рівномірний розподіл на [0;1]
Таблиця 3.4. Залежність величин 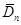 та та 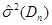 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
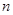
|
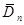 |
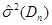 |
| Класичний метод |
Метод зменшення невизначеності |
Класичний метод |
Метод зменшення невизначеності |
| 3 |
0,433 |
0,190 |
0,024 |
0,007 |
| 4 |
0,362 |
0,190 |
0,012 |
0,008 |
| 5 |
0,338 |
0,198 |
0,005 |
0,003 |
| 6 |
0,301 |
0,190 |
0,006 |
0,004 |
| 7 |
0,292 |
0,193 |
0,009 |
0,007 |
| 8 |
0,275 |
0,192 |
0,009 |
0,006 |
| 9 |
0,253 |
0,177 |
0,004 |
0,004 |
| 10 |
0,241 |
0,174 |
0,003 |
0,003 |
| 11 |
0,235 |
0,173 |
0,003 |
0,003 |
| 12 |
0,223 |
0,168 |
0,004 |
0,003 |
| 13 |
0,217 |
0,166 |
0,003 |
0,002 |
| 14 |
0,204 |
0,157 |
0,003 |
0,003 |
| 15 |
0,200 |
0,156 |
0,002 |
0,002 |
За методом зменшення невизначеності для рівномірного на [0;1] розподілу знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 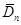 та та 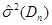 від обсягу вибірки n від обсягу вибірки n
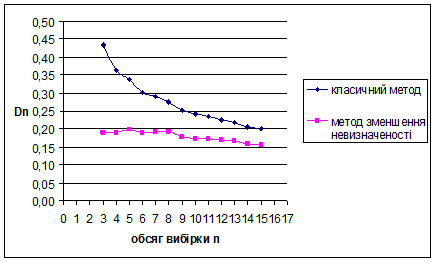
Рис. 3.7 Залежність величини 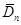 від обсягу вибірки n від обсягу вибірки n
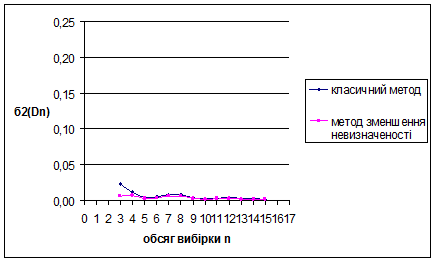
Рис. 3.8 Залежність величини 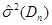 від обсягу вибірки n від обсягу вибірки n
Метод зменшення невизначеності
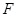 – нормальний розподіл N(1/2;1/36) – нормальний розподіл N(1/2;1/36)
Таблиця 3.5. Залежність величин 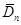 та та 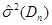 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
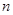
|
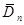 |
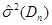 |
| Класичний метод |
Метод зменшення невизначеності |
Класичний метод |
Метод зменшення невизначеності |
| 3 |
0,443 |
0,256 |
0,018 |
0,016 |
| 4 |
0,412 |
0,259 |
0,020 |
0,015 |
| 5 |
0,359 |
0,244 |
0,012 |
0,009 |
| 6 |
0,296 |
0,204 |
0,011 |
0,010 |
| 7 |
0,314 |
0,221 |
0,015 |
0,013 |
| 8 |
0,276 |
0,210 |
0,011 |
0,008 |
| 9 |
0,265 |
0,194 |
0,006 |
0,004 |
| 10 |
0,256 |
0,192 |
0,007 |
0,006 |
| 11 |
0,216 |
0,169 |
0,004 |
0,003 |
| 12 |
0,214 |
0,169 |
0,005 |
0,004 |
| 13 |
0,201 |
0,169 |
0,003 |
0,002 |
| 14 |
0,190 |
0,158 |
0,005 |
0,004 |
| 15 |
0,194 |
0,157 |
0,003 |
0,003 |
За методом зменшення невизначеності для нормального розподілу N(1/2;1/36) знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий. Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 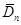 та та 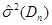 від обсягу вибірки n від обсягу вибірки n
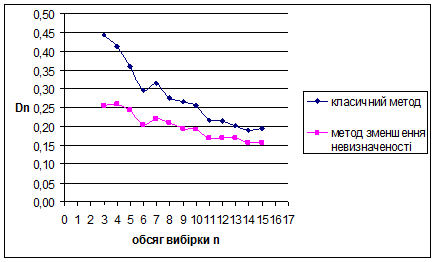
Рис. 3.9 Залежність величини 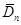 від обсягу вибірки n від обсягу вибірки n
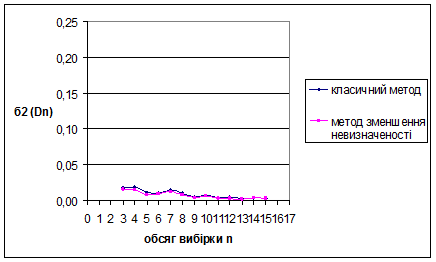
Рис. 3.10 Залежність величини 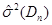 від обсягу вибірки n від обсягу вибірки n
Метод зменшення невизначеності
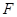 – експоненціальний розподіл з параметром λ=5 – експоненціальний розподіл з параметром λ=5
Таблиця 3.6. Залежність величин 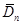 та та 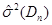 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
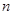
|
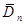 |
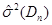 |
| Класичний метод |
Метод зменшення невизначеності |
Класичний метод |
Метод зменшення невизначеності |
| 3 |
0,442 |
0,252 |
0,030 |
0,022 |
| 4 |
0,383 |
0,260 |
0,014 |
0,010 |
| 5 |
0,360 |
0,263 |
0,012 |
0,013 |
| 6 |
0,308 |
0,225 |
0,011 |
0,011 |
| 7 |
0,264 |
0,186 |
0,004 |
0,002 |
| 8 |
0,246 |
0,185 |
0,006 |
0,006 |
| 9 |
0,253 |
0,183 |
0,005 |
0,005 |
| 10 |
0,226 |
0,171 |
0,005 |
0,005 |
| 11 |
0,226 |
0,169 |
0,004 |
0,003 |
| 12 |
0,207 |
0,160 |
0,002 |
0,002 |
| 13 |
0,220 |
0,156 |
0,002 |
0,002 |
| 14 |
0,219 |
0,164 |
0,004 |
0,003 |
| 15 |
0,201 |
0,158 |
0,004 |
0,003 |
За методом зменшення невизначеності для експоненціального розподілу з параметром λ=5 знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 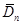 та та 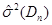 від обсягу вибірки n від обсягу вибірки n
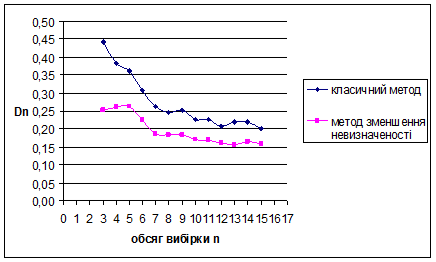
Рис. 3.11 Залежність величини 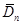 від обсягу вибірки n від обсягу вибірки n
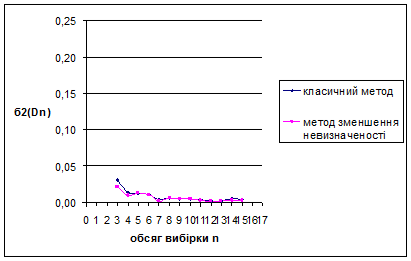
Рис. 3.12 Залежність величини 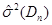 від обсягу вибірки n від обсягу вибірки n
Метод апріорно-емпіричних функцій
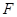 – рівномірний розподіл на [0;1] – рівномірний розподіл на [0;1]
Таблиця 3.7. Залежність величин 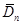 та та 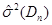 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
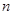
|
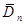 |
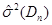 |
| Класичний метод |
Метод апріорно-емпіричних функцій |
Класичний метод |
Метод апріорно-емпіричних функцій |
| 3 |
0,413 |
0,044 |
0,011 |
0,000 |
| 4 |
0,387 |
0,040 |
0,012 |
0,000 |
| 5 |
0,320 |
0,041 |
0,012 |
0,000 |
| 6 |
0,302 |
0,040 |
0,009 |
0,000 |
| 7 |
0,303 |
0,043 |
0,008 |
0,000 |
| 8 |
0,279 |
0,040 |
0,007 |
0,000 |
| 9 |
0,275 |
0,040 |
0,003 |
0,000 |
| 10 |
0,234 |
0,034 |
0,002 |
0,000 |
| 11 |
0,229 |
0,032 |
0,005 |
0,000 |
| 12 |
0,240 |
0,037 |
0,004 |
0,000 |
| 13 |
0,219 |
0,033 |
0,002 |
0,000 |
| 14 |
0,199 |
0,032 |
0,006 |
0,000 |
| 15 |
0,209 |
0,033 |
0,004 |
0,000 |
За методом апріорно-емпіричних функцій для рівномірного на [0;1] розподілу знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 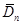 та та 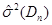 від обсягу вибірки n від обсягу вибірки n
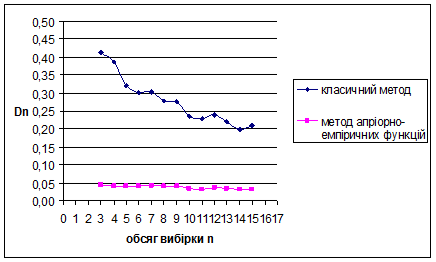
Рис. 3.13 Залежність величини 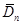 від обсягу вибірки n від обсягу вибірки n
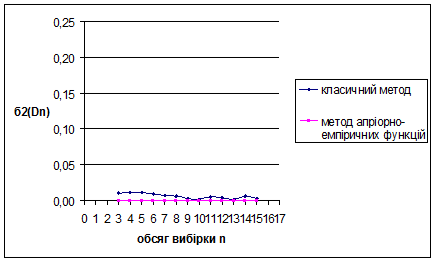
Рис. 3.14 Залежність величини 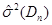 від обсягу вибірки n від обсягу вибірки n
Метод апріорно-емпіричних функцій
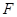 – нормальний розподіл N(1/2;1/36) – нормальний розподіл N(1/2;1/36)
Таблиця 3.8. Залежність величин 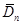 та та 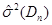 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
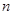
|
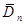 |
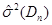 |
| Класичний метод |
Метод апріорно-емпіричних функцій |
Класичний метод |
Метод апріорно-емпіричних функцій |
| 3 |
0,508 |
0,226 |
0,019 |
0,012 |
| 4 |
0,421 |
0,186 |
0,014 |
0,013 |
| 5 |
0,335 |
0,178 |
0,013 |
0,005 |
| 6 |
0,288 |
0,171 |
0,004 |
0,003 |
| 7 |
0,290 |
0,161 |
0,005 |
0,004 |
| 8 |
0,264 |
0,135 |
0,006 |
0,004 |
| 9 |
0,250 |
0,141 |
0,006 |
0,001 |
| 10 |
0,227 |
0,142 |
0,004 |
0,003 |
| 11 |
0,227 |
0,133 |
0,004 |
0,002 |
| 12 |
0,212 |
0,137 |
0,005 |
0,002 |
| 13 |
0,207 |
0,139 |
0,004 |
0,002 |
| 14 |
0,214 |
0,136 |
0,005 |
0,002 |
| 15 |
0,208 |
0,133 |
0,004 |
0,002 |
За методом апріорно-емпіричних функцій для нормального розподілу N(1/2;1/36) знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 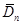 та та 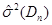 від обсягу вибірки n від обсягу вибірки n
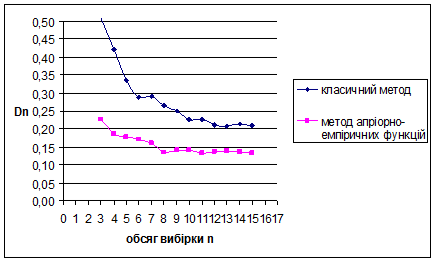
Рис. 3.15 Залежність величини 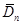 від обсягу вибірки n від обсягу вибірки n
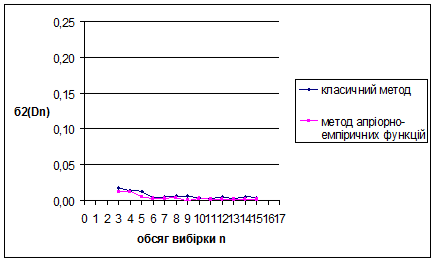
Рис. 3.16 Залежність величини 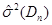 від обсягу вибірки n від обсягу вибірки n
Метод апріорно-емпіричних функцій
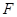 – експоненціальний розподіл з параметром λ=5 – експоненціальний розподіл з параметром λ=5
Таблиця 3.9. Залежність величин 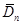 та та 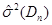 від обсягу вибірки n від обсягу вибірки n
Обсяг вибірки
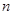
|
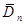 |
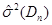 |
| Класичний метод |
Метод апріорно-емпіричних функцій |
Класичний метод |
Метод апріорно-емпіричних функцій |
| 3 |
0,446 |
0,235 |
0,014 |
0,007 |
| 4 |
0,440 |
0,234 |
0,014 |
0,012 |
| 5 |
0,345 |
0,229 |
0,007 |
0,009 |
| 6 |
0,343 |
0,197 |
0,012 |
0,008 |
| 7 |
0,298 |
0,196 |
0,008 |
0,011 |
| 8 |
0,297 |
0,188 |
0,008 |
0,007 |
| 9 |
0,250 |
0,186 |
0,003 |
0,005 |
| 10 |
0,243 |
0,184 |
0,006 |
0,004 |
| 11 |
0,239 |
0,183 |
0,008 |
0,007 |
| 12 |
0,220 |
0,173 |
0,005 |
0,004 |
| 13 |
0,220 |
0,170 |
0,003 |
0,004 |
| 14 |
0,222 |
0,170 |
0,003 |
0,003 |
| 15 |
0,217 |
0,164 |
0,003 |
0,005 |
За методом апріорно-емпіричних функцій для експоненціального розподілу з параметром λ=5 знайдено такі результати: метод виявився більш ефективним за класичний метод, внаслідок менших значень математичного сподівання вибірок. Оскільки дисперсія зі збільшенням обсягу вибірок зменшується, це свідчить про те, що метод стійкий.
Для наочності проілюструємо знайдені результати за допомогою графіків залежностей величин 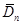 та та 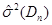 від обсягу вибірки n від обсягу вибірки n
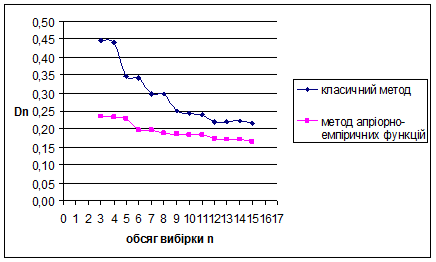
Рис. 3.17 Залежність величини 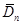 від обсягу вибірки n від обсягу вибірки n
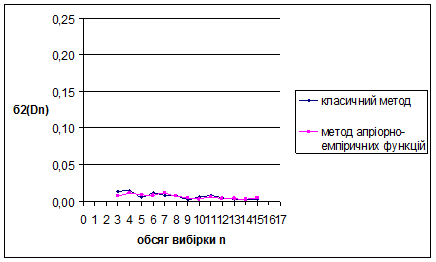
Рис. 3.18 Залежність величини 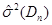 від обсягу вибірки n від обсягу вибірки n
Проведемо порівняння методів МПВ, МЗН та МАЕФ між собою за допомогою критеріїв:
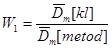 ;(3.1.3) ;(3.1.3)
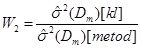 (3.1.4) (3.1.4)
де 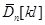 – математичне сподівання вибірки з колмогорівських відхилень, – математичне сподівання вибірки з колмогорівських відхилень,
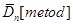 – математичне сподівання вибірки з відхилень, обчислених одним з трьох методів оцінювання функції розподілу малої вибірки, – математичне сподівання вибірки з відхилень, обчислених одним з трьох методів оцінювання функції розподілу малої вибірки,
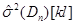 – дисперсія вибірки з колмогорівських відхилень, – дисперсія вибірки з колмогорівських відхилень,
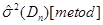 – дисперсія вибірки з відхилень, обчислених одним з трьох методів оцінювання функції розподілу малої вибірки. – дисперсія вибірки з відхилень, обчислених одним з трьох методів оцінювання функції розподілу малої вибірки.
Результати порівняння наведено в таблицях 3.10, 3.11.
Таблиця 3.10. Порівняння методу прямокутних внесків, методу зменшення невизначеності та методуапріорно-емпіричних функцій
| Обсяг вибірки |
Ефективність 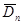 |
| Рівномірний розподіл |
Нормальний розподіл |
Експоненціальний розподіл |
| Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
| 3 |
2,750 |
2,284 |
9,286 |
1,282 |
1,733 |
2,249 |
1,541 |
1,749 |
1,897 |
| 4 |
2,618 |
1,908 |
9,593 |
1,181 |
1,592 |
2,263 |
1,312 |
1,472 |
1,879 |
| 5 |
2,726 |
1,705 |
7,721 |
1,119 |
1,473 |
1,880 |
1,147 |
1,369 |
1,506 |
| 6 |
2,680 |
1,585 |
7,556 |
1,007 |
1,455 |
1,688 |
1,051 |
1,370 |
1,736 |
| 7 |
2,263 |
1,514 |
6,978 |
0,844 |
1,421 |
1,804 |
1,055 |
1,415 |
1,523 |
| 8 |
2,369 |
1,429 |
6,948 |
0,815 |
1,313 |
1,956 |
1,037 |
1,331 |
1,579 |
| 9 |
2,371 |
1,424 |
6,875 |
0,818 |
1,369 |
1,776 |
1,042 |
1,378 |
1,342 |
| 10 |
2,255 |
1,388 |
6,857 |
0,805 |
1,331 |
1,601 |
1,050 |
1,324 |
1,322 |
| 11 |
2,151 |
1,353 |
7,069 |
0,682 |
1,283 |
1,711 |
0,866 |
1,333 |
1,303 |
| 12 |
1,938 |
1,332 |
6,478 |
0,577 |
1,266 |
1,546 |
0,785 |
1,293 |
1,271 |
| 13 |
1,991 |
1,308 |
6,570 |
0,647 |
1,187 |
1,496 |
0,792 |
1,408 |
1,293 |
| 14 |
2,366 |
1,299 |
6,115 |
0,554 |
1,206 |
1,574 |
0,746 |
1,339 |
1,305 |
| 15 |
2,094 |
1,280 |
6,330 |
0,555 |
1,234 |
1,566 |
0,718 |
1,271 |
1,318 |
Таблиця 3.11. Порівняння методу прямокутних внесків, методу зменшення невизначеності та методуапріорно-емпіричних функцій
| Обсяг вибірки |
Ефективність 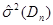 |
| Рівномірний розподіл |
Нормальний розподіл |
Експоненціальний розподіл |
| Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
Метод прямокутних внесків |
Метод зменшення невизначеності |
Метод апріорно-емпіричних функцій |
| 3 |
2,773 |
3,448 |
28,553 |
3,867 |
1,122 |
1,489 |
2,437 |
1,388 |
1,952 |
| 4 |
1,518 |
1,563 |
34,529 |
2,929 |
1,291 |
1,105 |
3,641 |
1,405 |
1,250 |
| 5 |
1,504 |
1,440 |
32,057 |
2,598 |
1,349 |
2,383 |
2,981 |
0,956 |
0,706 |
| 6 |
3,268 |
1,372 |
27,521 |
2,620 |
1,154 |
1,146 |
3,831 |
0,981 |
1,472 |
| 7 |
1,918 |
1,306 |
26,569 |
7,186 |
1,152 |
1,401 |
3,277 |
1,880 |
0,743 |
| 8 |
1,458 |
1,411 |
21,077 |
7,298 |
1,376 |
1,517 |
4,518 |
0,879 |
1,079 |
| 9 |
2,834 |
1,235 |
25,538 |
6,635 |
1,373 |
4,360 |
3,625 |
0,953 |
0,705 |
| 10 |
2,781 |
1,210 |
23,611 |
6,396 |
1,140 |
1,249 |
2,225 |
1,150 |
1,666 |
| 11 |
2,965 |
1,190 |
31,768 |
5,306 |
1,388 |
1,678 |
3,010 |
1,285 |
1,221 |
| 12 |
1,278 |
1,174 |
24,606 |
12,832 |
1,400 |
2,614 |
2,437 |
0,985 |
1,315 |
| 13 |
1,979 |
1,160 |
23,787 |
19,543 |
1,276 |
1,874 |
3,317 |
1,216 |
0,923 |
| 14 |
2,294 |
1,148 |
31,604 |
16,094 |
1,090 |
2,236 |
1,766 |
1,437 |
0,984 |
| 15 |
2,166 |
1,138 |
22,970 |
17,135 |
1,247 |
2,634 |
2,024 |
1,104 |
0,653 |
При порівнянні розглянутих сучасних методів між собою виявилось, що величини 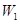 та та 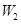 набагато більші для методу апріорно-емпіричних функцій, ніж для методу прямокутних внесків та методу зменшення невизначеності, внаслідок того, що математичне сподівання та дисперсія вибірок з відхилень (3.1.2) обернено пропорційні до величин набагато більші для методу апріорно-емпіричних функцій, ніж для методу прямокутних внесків та методу зменшення невизначеності, внаслідок того, що математичне сподівання та дисперсія вибірок з відхилень (3.1.2) обернено пропорційні до величин 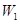 та та 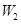 відповідно, а для методу апріорно-емпіричних функцій математичне сподівання та дисперсія вибірки з відхилень (3.1.2) набагато менші за математичне сподівання та дисперсію вибіркок з відхилень, обчислених за двома іншими методами. Це свідчить про те, що метод апріорно-емпіричних функцій є більш ефективним за метод прямокутних внесків та метод зменшення невизначеності. Це пов’язано з тим, що в методі апроіорно-емпіричних функцій, на відміну від методу прямокутних внесків та методу зменшення невизначеності, введено коефіцієнт достовірності апріорної інформації, який можна корегувати в залежності від конкретної ситуації. Це дійсно є важливим кроком вперед, тому що на практиці дані, які аналізує статистик, можуть мати різноманітну природу. відповідно, а для методу апріорно-емпіричних функцій математичне сподівання та дисперсія вибірки з відхилень (3.1.2) набагато менші за математичне сподівання та дисперсію вибіркок з відхилень, обчислених за двома іншими методами. Це свідчить про те, що метод апріорно-емпіричних функцій є більш ефективним за метод прямокутних внесків та метод зменшення невизначеності. Це пов’язано з тим, що в методі апроіорно-емпіричних функцій, на відміну від методу прямокутних внесків та методу зменшення невизначеності, введено коефіцієнт достовірності апріорної інформації, який можна корегувати в залежності від конкретної ситуації. Це дійсно є важливим кроком вперед, тому що на практиці дані, які аналізує статистик, можуть мати різноманітну природу.
Проілюструємо знайдені результати за допомогою графіків.
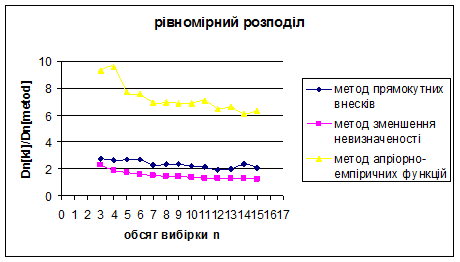
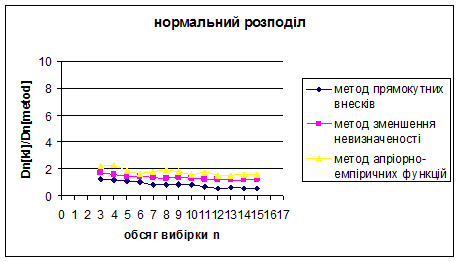
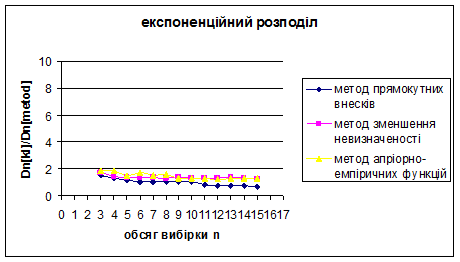
Рис. 3.19 – 3.21 Порівняння методу прямокутних внесків, методу зменшення невизначеності та методу апріорно-емпіричних функцій
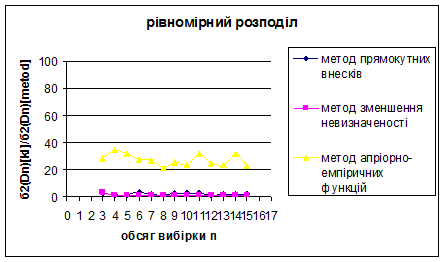
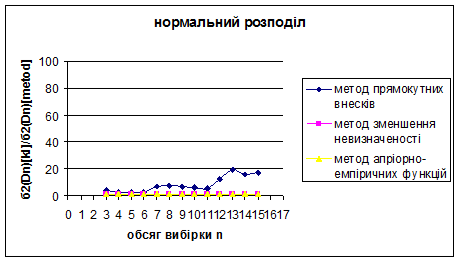
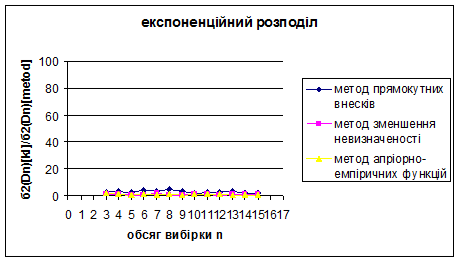
Рис. 3.22 – 3.24 Порівняння методу прямокутних внесків, методу зменшення невизначеності та методу апріорно-емпіричних функцій
З курсу матаматичної статистики відомо, що відхилення емпіричної функції від гіпотетичної, побудоване за формулою (3.1.1) при достатньо великих n має колмогорівський розподіл. За допомогою критерія Смірнова перевіримо гіпотезу про те, що відхилення, побудоване за формулою (3.1.2), має розподіл Колмогорова. Результати перевірки гіпотези наведено в таблицях 3.12-3.14.
Таблиця 3.12 Відхилення Смірнова
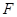 – рівномірний розподіл на [0;1] – рівномірний розподіл на [0;1] |
Обсяг вибірки 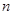 |
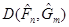 для методу прямокутних внесків для методу прямокутних внесків |
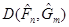 для методу зменшення невизначеності для методу зменшення невизначеності |
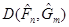 для методу апріорно-емпіричних функцій для методу апріорно-емпіричних функцій |
| 3 |
2,85 |
2,85 |
3,00 |
| 4 |
2,69 |
2,21 |
3,00 |
| 5 |
2,69 |
2,53 |
3,00 |
| 6 |
3,00 |
2,53 |
3,00 |
| 7 |
2,21 |
1,90 |
3,00 |
| 8 |
2,53 |
1,42 |
3,00 |
| 9 |
2,53 |
1,74 |
3,00 |
| 10 |
2,21 |
1,74 |
3,00 |
| 11 |
2,85 |
1,74 |
3,00 |
| 12 |
2,53 |
1,11 |
3,00 |
| 13 |
2,85 |
1,74 |
3,00 |
| 14 |
2,85 |
1,74 |
3,00 |
| 15 |
2,37 |
1,42 |
3,00 |
Таблиця 3.13 Відхилення Смірнова
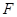 – нормальний розподіл N(1/2;1/36) – нормальний розподіл N(1/2;1/36) |
Обсяг вибірки 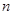 |
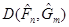 для методу прямокутних внесків для методу прямокутних внесків |
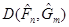 для методу зменшення невизначеності для методу зменшення невизначеності |
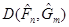 для методу апріорно-емпіричних функцій для методу апріорно-емпіричних функцій |
| 3 |
1,26 |
2,37 |
2,53 |
| 4 |
1,11 |
1,42 |
2,53 |
| 5 |
1,26 |
1,90 |
2,06 |
| 6 |
0,63 |
1,26 |
2,53 |
| 7 |
2,21 |
1,58 |
2,37 |
| 8 |
2,21 |
1,26 |
2,37 |
| 9 |
2,53 |
1,74 |
2,53 |
| 10 |
2,85 |
1,26 |
1,74 |
| 11 |
2,53 |
1,42 |
2,21 |
| 12 |
3,00 |
1,42 |
1,74 |
| 13 |
2,69 |
1,26 |
1,74 |
| 14 |
3,00 |
0,79 |
1,74 |
| 15 |
2,85 |
1,11 |
1,90 |
Таблиця 3.14 Відхилення Смірнова
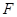 – експоненціальний розподіл з параметром λ=5 – експоненціальний розподіл з параметром λ=5 |
Обсяг вибірки 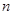 |
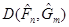 для методу прямокутних внесків для методу прямокутних внесків |
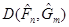 для методу зменшення невизначеності для методу зменшення невизначеності |
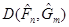 для методу апріорно-емпіричних функцій для методу апріорно-емпіричних функцій |
| 3 |
2,06 |
1,74 |
2,37 |
| 4 |
1,90 |
2,53 |
1,74 |
| 5 |
0,95 |
1,11 |
1,74 |
| 6 |
0,79 |
1,26 |
1,90 |
| 7 |
0,95 |
2,06 |
2,21 |
| 8 |
1,11 |
1,58 |
1,26 |
| 9 |
0,63 |
1,58 |
1,26 |
| 10 |
0,95 |
1,42 |
1,58 |
| 11 |
1,90 |
1,42 |
1,74 |
| 12 |
2,06 |
1,42 |
1,42 |
| 13 |
1,90 |
1,74 |
0,95 |
| 14 |
2,53 |
1,90 |
1,42 |
| 15 |
2,21 |
1,11 |
1,42 |
Відхилення Смірнова
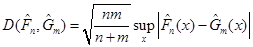 , ,
обчислене для кожного з методів порівнювалось з 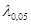 – верхньою – верхньою 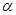 – границею розподілу Колмогорова ( – границею розподілу Колмогорова (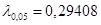 ). Оскільки ). Оскільки
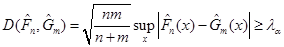 , ,
отже, гіпотеза про розподіл Колмогорова, відхилення (3.1.2), відхиляється.
Висновки
Для математичної статистики проблема малої вибірки завжди є цікавою та актуальною.
Трудоємність та матеріальні затрати не завжди дозволяють провести стохастичний експеримент достатню кількість разів для знаходження вибірки потрібного обсягу, тому на практиці доводиться приймати рішення, аналізуючи вибірку малого обсягу.
В сучасній науковій літературі відомості з цього питання різносторонні. Деякі автори вважають малими вибірками вибірки обсягом до 200 спостережень, інші автори називають малими вибірками вибірки обсягом до 50 спостережень. Експериментально встановлено, що для знаходження стійких оцінок необхідна вибірка обсягом 40-50 спостережень. На сьогоднішній день відкритим питанням залишається строго математичне означення малої вибірки.
Вибіркою малого обсягу, або малою вибіркою будемо називати вибірку, для аналізу якої не можна використати асимптотичні методи.
На практиці часто виникає питання: як оцінити розподіл малої вибірки? Яким методом? Адже методи, які засновані на групуванні вибіркових значень, застосовувати до малої вибірки неможна.
В дипломній роботі ставиться задача порівняння класичного методу оцінювання розподілу вибірки, в основі якого лежить побудова емпіричної функції розподілу, та сучасних методів оцінювання розподілу малої вибірки.
Розглянемо кожен з методів. Почнемо з класичного. Нехай 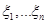 – вибірка з неперервного розподілу F. Функцію, визначену рівністю – вибірка з неперервного розподілу F. Функцію, визначену рівністю
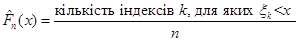
називають емпіричною функцією розподілу. Емпірична функція розподілу є незміщеною та спроможною оцінкою функції розподілу F(x). За міру відхилення функції розподілу 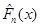 від функції розподілу від функції розподілу 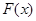 будемо розглядати міру, запропоновану А. М. Колмогоровим: будемо розглядати міру, запропоновану А. М. Колмогоровим:
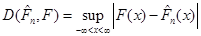
Розглянемо три методи оцінювання функції розподілу малої вибірки. Ці методи мають спільну ідею побудови оцінки функції розподілу, яка полягає в таких припущеннях: множина можливих значень випадкових величин 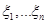 – відрізок [a,b], кожна випадкова величина використовується для побудови оцінки щільності окремо, при цьому кожна випадкова величина рівномірно "розмазується" в деякій області. – відрізок [a,b], кожна випадкова величина використовується для побудови оцінки щільності окремо, при цьому кожна випадкова величина рівномірно "розмазується" в деякій області.
Для всіх методів оцінка щільності розподілу складається з двох компонент: апріорної та апостеріорної:
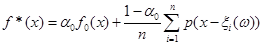
Різним методам оцінювання відповідають різні значення ваги 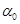 та різні внески апостеріорої компоненти. та різні внески апостеріорої компоненти.
Розглянемо докладніше перший метод.
Метод прямокутних внесків був запропонований Чавчанідзе В.В. та Кумсішвілі В.А. в 1959 році.
Жодній випадковій величині з відрізка [а;b] не можна віддати перевагу. Саме таку властивість має рівномірний розподіл, щільність якого
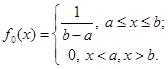
будемо називати апріорною щільністю розподілу.

За вагу 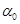 приймається величина приймається величина 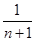 . .
Далі проводиться стохастичний експеримент, результатом якого є реалізація 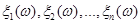 вибірки вибірки 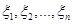 з відомого неперевного розподілу з відомого неперевного розподілу 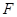 . За допомогою цієї реалізації можна уточнити апріорну щільність розподілу. . За допомогою цієї реалізації можна уточнити апріорну щільність розподілу.
Реалізація 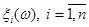 рівномірно "розмазується" в прямокутнику рівномірно "розмазується" в прямокутнику
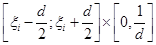
А саме: припишемо кожній реалізації 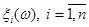 елементарну рівномірну щільність на відрізку елементарну рівномірну щільність на відрізку 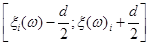 : :
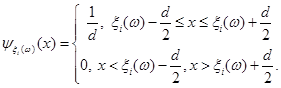
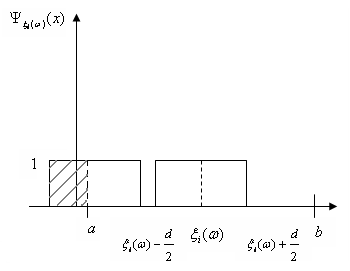
При цьому для прямокутників, що виходять за межі інтервалу 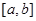 , необхідно відкидати частини, які виходять за межі, а над частиною внеску, що знаходиться всередині відрізку , необхідно відкидати частини, які виходять за межі, а над частиною внеску, що знаходиться всередині відрізку 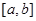 , як над основою, слід рівномірно надбудовувати прямокутник, площа якого дорівнює відкинутій. , як над основою, слід рівномірно надбудовувати прямокутник, площа якого дорівнює відкинутій.
Тоді оцінка щільності розподілу малої вибірки має вигляд
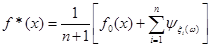
Оцінка функції розподілу F*(x) знаходиться інтегруванням щільності.
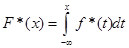
Наступний метод – метод зменшення невизначеності був запропонований Єременко В.І. та Свердликом А.Н. в 1963 році.
В цьому методі за апріорну компоненту також береться рівномірний розподіл, а за вагу 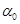 - величина - величина 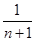 . .
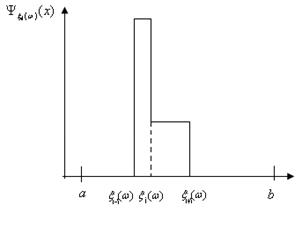
На відміну від МПВ, випадкова величина рівномірно "розмазується" у внеску східчатої форми, вигляду
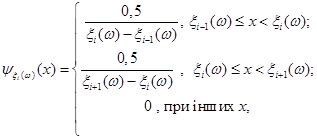
який складається з двох прямокутників однакової площі. Така заміна дозволяє досить легко будувати оцінку щільності розподілу, але виграшу вефективності дати не може, тому, що ширина внеску 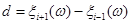 є випадкова величина. є випадкова величина.

Наступний метод – метод апріорно-емпіричних функцій був запропонований Демковим І.П. та Потепун В.Е. в 1970 році.
Оцінка, побудована методом апріорно-емпіричних функцій, визначається формулою:
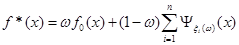 , ,
де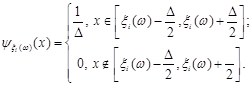
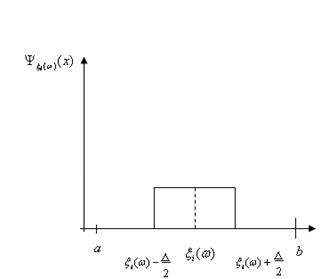
ширина внеску визначається тільки точністюапаратури 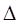 . В цьому істотна слабкість методу, оскільки зі зміною точності вимірювань (появи більш досконалого приладу) буде змінюватись ефективність оцінювання. Але цей метод має і сильну сторону. Ввведення коефіцієнта достовірності інформації , . В цьому істотна слабкість методу, оскільки зі зміною точності вимірювань (появи більш досконалого приладу) буде змінюватись ефективність оцінювання. Але цей метод має і сильну сторону. Ввведення коефіцієнта достовірності інформації ,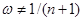 , який можна корегувати в залежності від конкретної ситуації, відрізняє метод АЕФ від попередніх. Це дійсно є важливим кроком вперед, тому що на практиці дані, які аналізує статистик, можуть мати різноманітну природу. , який можна корегувати в залежності від конкретної ситуації, відрізняє метод АЕФ від попередніх. Це дійсно є важливим кроком вперед, тому що на практиці дані, які аналізує статистик, можуть мати різноманітну природу.
В дипломній роботі проведено експеримент, в якому кожен з трьох методів було порівняно з класичним методом.
Добувалась реалізація 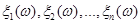 вибірки вибірки 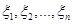 з відомого розподілу з відомого розподілу 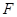 . Будувалася емпірична функція розподілу та оцінка функції розподілу одним з трьох методів оцінювання функції розподілу малої вибірки. Далі обчислювалось колмогорівське відхилення емпіричної функції розподілу від гіпотетичної . Будувалася емпірична функція розподілу та оцінка функції розподілу одним з трьох методів оцінювання функції розподілу малої вибірки. Далі обчислювалось колмогорівське відхилення емпіричної функції розподілу від гіпотетичної
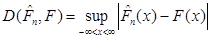 , ,
а також відхилення побудоване аналогічно колмогорівському
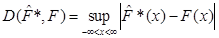 , ,
в якому замість емпіричної функції розподілу береться оцінка функції розподілу 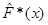 , обчислена одним з трьох методів оцінювання функції розподілу малої вибірки (МПВ, МЗН, МАЕФ). , обчислена одним з трьох методів оцінювання функції розподілу малої вибірки (МПВ, МЗН, МАЕФ).
Відхилення порівнювались так: фіксувався обсяг вибірки n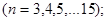 добувалось 20 реалізацій вибірки добувалось 20 реалізацій вибірки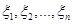 ; обчислювалось 20 відхилень вигляду ; обчислювалось 20 відхилень вигляду 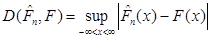 та та 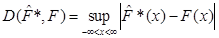 , рахувалось середнє та дисперсія вибірок даних відхилень. , рахувалось середнє та дисперсія вибірок даних відхилень.
За розподіл 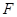 розглядались рівномірний, нормальний та експоненціальний розподіли. розглядались рівномірний, нормальний та експоненціальний розподіли.
За методом прямокутних внесків знайдено такі результати.
Для рівномірного на [0;1] розподілу метод виявився більш ефективним за класичний метод, в тому сенсі, що середні значення відхилень, знайдені методом прямокутних внесків, менші за середні відхилення, знайдені класичним методом.
Для нормального N(1/2;1/36) та експоненціального з параметром 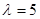 розподілів метод виявився більш ефективним за класичний метод для вибірок обсягом менше ніж 6 та 10 спостережень відповідно. Для вибірок більшого обсягу метод не ефективний – це обумовлено тим, що за апріорну інформацію приймається рівномірний на [0;1] розподіл. розподілів метод виявився більш ефективним за класичний метод для вибірок обсягом менше ніж 6 та 10 спостережень відповідно. Для вибірок більшого обсягу метод не ефективний – це обумовлено тим, що за апріорну інформацію приймається рівномірний на [0;1] розподіл.
За методом зменшення невизначеності та методом апріорно-емпіричних функцій отримано такі результати.
Для всіх розглянутих розподілів методи виявилися більш ефективними за класичний метод. Середні значення відхилень, знайдені даними методоми, менші за середні відхилення, знайдені класичним методом. Оскільки дисперсія зі збільшенням обсягу вибірки зменшується методи можна вважати стійкими.
Крім цього експерименту було проведено порівняння методів МПВ, МЗН та МАЕФ між собою.
При порівнянні виявилось, що метод апріорно-емпіричних функцій ефективніший ніж метод прямокутних внесків та метод зменшення невизначеності, внаслідок того, що відхилення 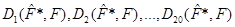 набагато менші за відхилення набагато менші за відхилення 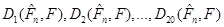 , знайдені класичним методом. Це пов’язано з тим, що в методі апроіорно-емпіричних функцій, на відміну від методу прямокутних внесків та методу зменшення невизначеності, введено коефіцієнт достовірності апріорної інформації. , знайдені класичним методом. Це пов’язано з тим, що в методі апроіорно-емпіричних функцій, на відміну від методу прямокутних внесків та методу зменшення невизначеності, введено коефіцієнт достовірності апріорної інформації.
Список використаних джерел
1. Турчин В.Н., Теория вероятностей и математическая статистика: В 2 т. - Т.2: Математическая статистика, Днепропетровск: ДГУ, 1996. - 248 с.
2. Турчин В.М., Математична статистика, К.: "Академія", 1999. – 240 с.
3. Гаскаров Д.В., Шаповалов В.И. Малая выборка. М., "Статистика", 1978. – 248 с.
4. Чавчанидзе В.В., Кумсишвили В.А., Об определении законов распределения на основе малого числа наблюдений. – В кн.: Применение вычислительной техники для автоматизации производства (Труды совещания 1959 г.). М., Машгиз, 1961, с. 71-75.
5. Еременко И.В., Свердлик А.Н. Об одном методе построения законов распределения величин при малом числе испытаний. – В кн.: Некоторые вопросы специального применения вычислительной техники. Л., ЛВИКА им.А.Ф. Можайского, 1963, с. 18 – 29.
6. Демаков И.П., Потепун В.Е. Статистические методы определения законов распределения при анализе точности и надежности промышленных изделий по результатам эксперимента. Л., 1970. 39 с.
7. Методы статистического анализа и обработка малого числа наблюдений при контроле качества и надежности приборов и машин. Л., 1974. 92 с.
8. Березин О.П. Определение законов распределения малых выборок методом прямоугольных вкладов. – Доклады к НТК по надежности судового электрооборудования, вып. 65. Л., 1965, с. 190 – 198.
9. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. – 2-е изд., дополн. – М.: Наука, 1982. – 296 с.
10. Корн Г., Корн Т. Справочник по математике. М., Наука, 1970. 720 с.
|