МИНИСТЕРСТВО СЕЛЬСКОГОХОЗЯЙСТВА РФ
ДЕПАРТАМЕНТ НАУЧНО – ТЕХНОЛОГИЧЕСКОЙ
ПОЛИТИКИ И ОБРАЗОВАНИЯ
ФГОУ ВПО «ПРИМОРСКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
ИНСТИТУТ ЭКОНОМИКИ И БИЗНЕСА
Реферат
Тема: «Функция»
Выполнил: Ярмонтович Д.А.
Проверила:
УССУРИЙСК 2006
СОДЕРЖАНИЕ
· 1)Введние
· 2)Линейная функция
· 3)Квадратичная функция
· 4)Степенная функция
· 5)Показательная функция (экспонента)
· 6)Логарифмическая функция
· 7)Тригонометрическая функция
· -Функция синус
·
-Функция косинус· -Функция тангенс
· -Функция котангенс
· 8)Обратная функция
· -Arcsinx
· -Arctgx
· 9)Список Литературы
введение
К элементарным функциям относятся рациональные, степенные, показательная и логарифмические функции, а также тригонометрические и обратные тригонометрические функции. К классу элементарных функций, кроме того, относят также сложные функции, образованные из перечисленных выше элементарных функций.
Функция-
зависимость переменной у
от переменной x
,
если каждому значению х
соответствует единственное значение у
.
Переменная х -
независимая переменная или аргумент.
Переменная у -
зависимая переменная
Значение функции -
значение у
, соответствующее заданному значению х
.
Область определения функции-
все значения, которые принимает независимая переменная.
Область значений функции (множество значений)-
все значения, которые принимает функция.
Функция является четной -
если для любого х
из области определения функции выполняется равенство f
(
x
)=
f
(-
x
)
Функция является нечетной -
если для любого х
из области определения функции выполняется равенство f
(-
x
)=-
f
(
x
)
Возрастающая функция -
если для любых х1
и х2
,
таких, что х1
< х2
, выполняется неравенство f
(х1
)<
f
(х2
)
Убывающая функция -
если для любых х1
и х2
,
таких, что х1
< х2
, выполняется неравенство f
(х1
)>
f
(х2
)
Линейная функция.
Это функция вида 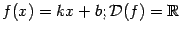 . Число . Число 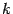 называется угловым коэффициентом
, а число называется угловым коэффициентом
, а число 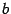 - свободным членом
. Графиком - свободным членом
. Графиком 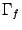 линейной функции служит прямая на координатной плоскости линейной функции служит прямая на координатной плоскости 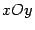 , не параллельная оси , не параллельная оси 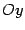 . .
Угловой коэффициент 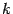 равен тангенсу угла равен тангенсу угла 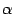 наклона графика наклона графика 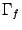 к горизонтальному направлению - положительному направлению оси к горизонтальному направлению - положительному направлению оси 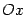 . .
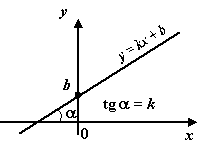
График линейной функции - прямая
1. Область определения – все действительные числа.
2. Область значений – все действительные числа.
3. Если k=0, то график будет параллелен оси абсцисс и будет проходить через точку (0; b).
4. Линейная функция ни четная ни нечетная.
5. Функция возрастает если k>0,
Реклама

Функция убывает если k<0.
6. Функция непрерывна.
Квадратичная функция.
Это функция вида 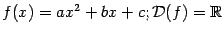 , ,
Графиком 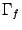 квадратичной функции служит парабола
с осью, параллельной оси квадратичной функции служит парабола
с осью, параллельной оси 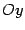 . При . При 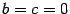 вершина параболы оказывается в точке вершина параболы оказывается в точке 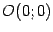 . .
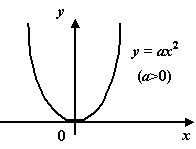
Парабола 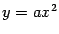 ( (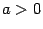 ) )
В общем случае вершина лежит в точке 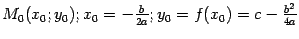 . Если . Если 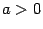 , то "рога" параболы направлены вверх, если , то "рога" параболы направлены вверх, если 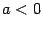 , то вниз. , то вниз.
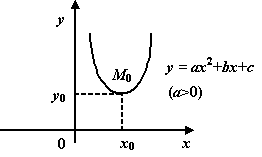
.Парабола с вершиной в точке 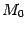 ( (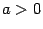 ) )
1.
Область определения квадратичной функции – вся числовая прямая.
2.
При b
¹0 функция не является четной и не является нечетной. При b
=0 квадратичная функция – четная.
3.
Рис. 4 Рис. 54.
Квадратичная функция непрерывна и дифференцируема во всей области определения.
5.
Функция имеет единственную критическую точку
6.
x
=-
b
/(2
a
)
. Если a
>0, то в точке x
=-
b
/(2
a
)
функция имеет минимум. При x
<-
b
/(2
a
)
функция монотонно убывает, при x
>-
b
/(2
a
)
монотонно возрастает.
a. Если а
<0, то в точке x
=-
b
/(2
a
)
функция имеет максимум. При x
<-
b
/(2
a
)
функция монотонно возрастает, при x
>-
b
/(2
a
)
монотонно убывает.
b. Точка графика квадратичной функции с абсциссой x
=-
b
/(2
a
)
и ординатой y
= -((
b
2
-4
ac
)/4
a
)
называется вершиной параболы
.
7.
Область изменения функции: при a
>0 – множество значений функции [-((
b
2
-4
ac
)/4
a
); +
¥
)
; при a
<0 – множество значений функции (-
¥
;-((
b
2
-4
ac
)/4
a
)]
.
8.
График квадратичной функции пересекается с осью 0
y
в точке y
=
c
. В случае, если b
2
-4
ac
>0
, график квадратичной функции пересекает ось 0
x
в двух точках (различные действительные корни квадратного уравнения); если b
2
-4
ac
=0
(квадратное уравнение имеет один корень кратности 2), график квадратичной функции касается оси 0x
в точке x
=-
b
/(2
a
)
; если b
2
-4
ac
<0
, пересечения с осью 0
x
нет.
a. Из представления квадратичной функции в виде (1) также следует, что график функции симметричен относительно прямой x
=-
b
/(2
a
)
– образа оси ординат при параллельном переносе r
=(-
b
/(2
a
); 0)
.
b. График функции
9.
f
(
x
)=
ax
2
+
bx
+
c
10.
(или f
(
x
)=
a
(
x
+
b
/(2
a
))2
-(
b
2
-4
ac
)/(4
a
))
может быть получен из графика функции f
(
x
)=
x
2
следующими преобразованиями:
а) параллельным переносом r
=(-
b
/(2
a
); 0)
;
б) сжатием (или растяжением) к оси абсцисс в а
раз;
Реклама

в) параллельным переносом r
=(0; -((
b
2
-4
ac
)/(4
a
)))
.
Степенная функция.
Это функция вида 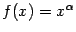 , , 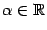 . Рассматриваются такие случаи: . Рассматриваются такие случаи:
а). Если 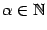 , то , то 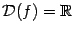 . Тогда . Тогда 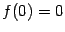 , , 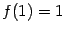 ; если число ; если число 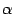 - чётное, то и функция - чётное, то и функция 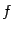 - чётная (то есть - чётная (то есть 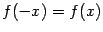 при всех при всех 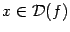 ); если число ); если число 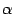 - нечётное, то и функция - нечётное, то и функция 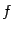 - нечётная (то есть - нечётная (то есть 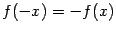 при всех при всех 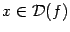 ). ).
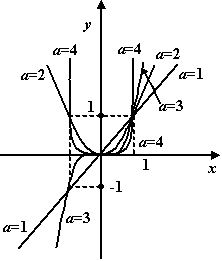
График степенной функции при 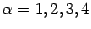
б) Если 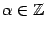 , , 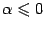 , то , то 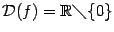 . Ситуация с чётностью и нечётностью при этом такая же, как и для . Ситуация с чётностью и нечётностью при этом такая же, как и для 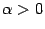 : если : если 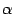 - чётное число, то и - чётное число, то и 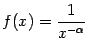 - чётная функция; если - чётная функция; если 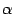 - нечётное число, то и - нечётное число, то и 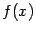 - нечётная функция. - нечётная функция.
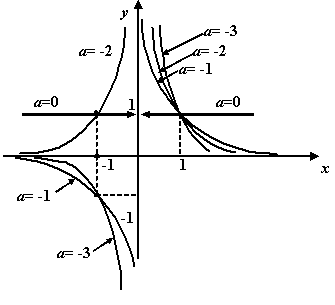
График степенной функции при 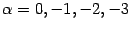
Снова заметим, что 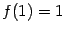 при всех при всех 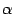 . Если . Если 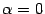 , то , то 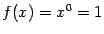 при всех при всех 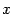 , кроме , кроме 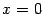 (выражение (выражение 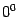 не имеет смысла). не имеет смысла).
в). Если 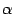 - не целое число, то, по определению, при - не целое число, то, по определению, при 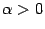 : : 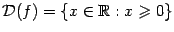 ; тогда ; тогда 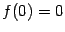 , , 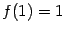 . .
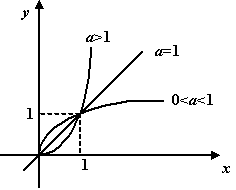
График степенной функции при 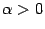
При 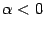 , по определению, , по определению, 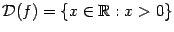 ; тогда ; тогда 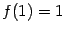 . .
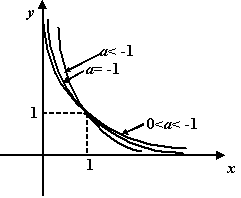
График степенной функции при 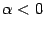
1. Область определения степенной функции – множество всех положительных чисел.
2. Область значения степенной функции – множество всех положительных чисел.
3. Степенная функция непериодична, не является четной и не является нечетной.
4. Степенная функция непрерывна во всей области определения.
5. Степенная функция дифференцируема во всей области определения, и ее производная вычисляется по формуле
(
x
a
)
¢
=
a
.
x
a
-1
.
Степенная функция x
a
монотонно возрастает во всей области определения при a
<0.
6.
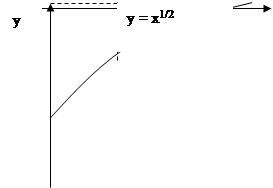
0 1 x 0 1 x
7. При a
<0 и a
>1 график степенной функции направлен вогнутостью вверх, а при 0<a
<1 – вогнутостью вниз.
Показательная функция (экспонента).
Это функция вида 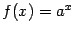 ( (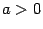 , , 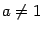 ). Для неё ). Для неё 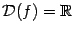 , , 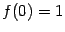 , , 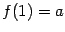 , и при , и при 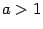 график имеет такой вид: график имеет такой вид:
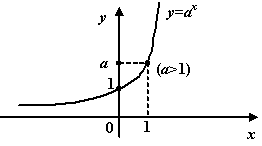
.График показательной функции при 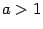
При 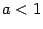 вид графика такой: вид графика такой:
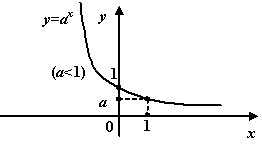
Рис.1.20.График показательной функции при 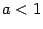
1. Число 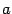 называется основанием
показательной функции. Область определения функции – вся числовая прямая. называется основанием
показательной функции. Область определения функции – вся числовая прямая.
2. Область значения функции – множество всех положительных чисел.
3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле
(a
x
)¢ =a
x
lna
4. При а
>1 функция монотонно возрастает, при а
<1 монотонно убывает.
5. Показательная функция имеет обратную функцию, называемую логарифмической функцией.
6. График любой показательной функции пересекает ось 0y
в точке y
=1.
7. График показательной функции – кривая, направленная вогнутостью вверх.
Логарифмическа
я
функция
.
Это функция вида 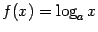 ( (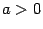 , , 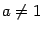 ). Для неё ). Для неё 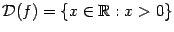 , , 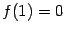 , , 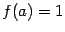 , и при , и при 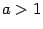 график имеет такой вид: график имеет такой вид:
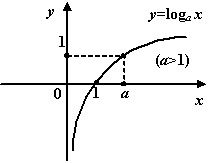
График логарифмической функции при 
При  график получается такой: график получается такой:
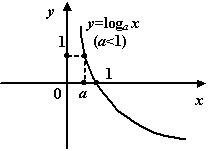
График логарифмической функции при 
1. Число 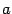 называется основанием
логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия. Область определения логарифмической функции – промежуток (0; +¥). называется основанием
логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия. Область определения логарифмической функции – промежуток (0; +¥).
2. Область значения логарифмической функции – вся числовая прчмая.
3. Логарифмическая функция непрерывна и дифференцируема во всей области определения. Производная логарифмической функции вычисляется по формуле
(
loga
x)
¢
= 1/(x ln a).
4. Логарифмическая функция монотонно возрастает, если а
>1. При 0<a
<1 логарифмическая функция с основанием а
монотонно убывает.
5. При любом основании a
>0, a
¹1, имеют место равенства
loga
1
=
0, loga
a
=1.
6. При а
>1 график логарифмической функции – кривая, направленная вогнутостью вниз; при 0<a
<1 – кривая, направленная вогнутостью вверх.
тригонометрические функции
Функции sin
a
,
cos
a
,
tg
a
,
ctg
a
называются тригонометрическими функциями
угла a. Кроме основных тригонометрических функций sina, cosa, tga, ctga.
Функция синус
.
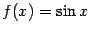 . Для неё . Для неё 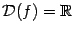 ; функция периодична с периодом ; функция периодична с периодом 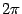 и нечётна. Её график таков: и нечётна. Её график таков:
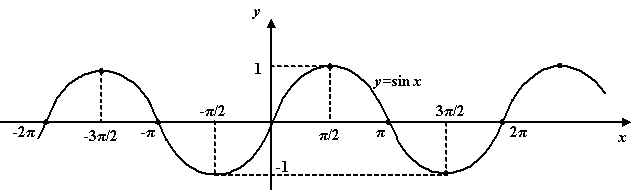
График функции 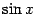
Синусом
числа х
называется число, равное синусу угла в радианах.
1. Область определения – множество всех действительных чисел.
2. Область значения – промежуток [-1; 1].
3. Функцияsin х – нечетная: sin (-х)=- sin х.
4. Функция sin х – периодическая. Наименьший положительный период равен 2p:
sin (х+2p)= sin х.
5. Нули функции: sin х=0 при x=pn, n
ÎZ
.
6. Промежутки знакопостоянства:
sin х>0 при xÎ (2pn
; p+2pn
), n
ÎZ
,
sin х<0 при xÎ (p+2pn
; 2p+2pn
), n
ÎZ
.
7. Функция sin х непрерывна и имеет производную при любом значении аргумента:
(sin х)¢ =cos x.
8. Функция sin х возрастает при xÎ ((-p/2)+2pn;
(p/2)+2pn
), n
ÎZ
,
и убывает при xÎ ((p/2)+2pn
; ((3p)/2)+ 2pn
), n
ÎZ
.
9. Функция sin х имеет минимальные значения, равные –1, при х=(-p/2)+2pn
, n
ÎZ
, и максимальные значения, равные 1, при х=(p/2)+2pn
, n
ÎZ
.
Функция косинус.
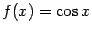 . Эта функция связана с синусом формулой приведения: . Эта функция связана с синусом формулой приведения: 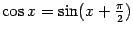 ; ; 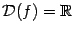 ; период функции ; период функции 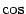 равен равен 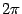 ; функция ; функция 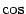 чётна. Её график таков: чётна. Её график таков:
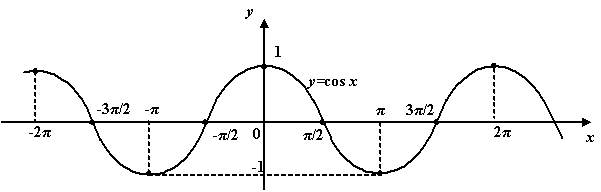
1.График функции 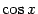 Область определения – множество всех действительных чисел. Область определения – множество всех действительных чисел.
2.Область значения – промежуток [-1; 1].
3.Функцияcos х – четная: cos (-х)=cos х.
4.Функция cos х – периодическая. Наименьший положительный период равен 2p:
cos (х+2p)= cos х.
5.Нули функции: cosх=0 при x=(p/2)+2pn, n
ÎZ
.
6.Промежутки знакопостоянства:
cos х>0 при xÎ ((-p/2)+2pn;
(p/2)+2pn
)), n
ÎZ
,
cos х<0 при xÎ ((p/2)+2pn
); ((3p)/2)+ 2pn
)), n
ÎZ
.
7.Функция cos х непрерывна и дифференцируема при любом значении аргумента:
(cos х)¢ =-sin x.
8.Функция cos х возрастает при xÎ (-p+2pn;
2pn
), n
ÎZ
,
и убывает при xÎ (2pn
; p+ 2pn
), n
ÎZ
.
Функция cos х имеет минимальные значения, равные –1, при х=p+2pn
, n
ÎZ
, и максимальные
Функция тангенс.
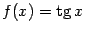 (в англоязычной литературе обозначается также (в англоязычной литературе обозначается также 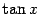 ). По определению, ). По определению, 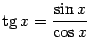 . Функция . Функция 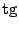 нечётна и периодична с периодом нечётна и периодична с периодом 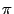 ; ;
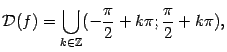
то есть 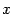 не может принимать значений не может принимать значений 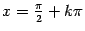 , , 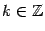 , при которых , при которых 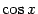 (стоящий в знаменателе) обращается в ноль. (стоящий в знаменателе) обращается в ноль.
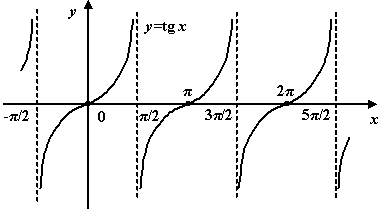
1.График функции 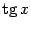 Область определения функции – множество всех действительных чисел, кроме числа х=p/2+pn
, n
ÎZ
. Область определения функции – множество всех действительных чисел, кроме числа х=p/2+pn
, n
ÎZ
.
2.Область значения – множество всех действительных чисел.
3.Функцияtg х – нечетная: tg (-х)=- tg х.
4.Функция tg х – периодическая. Наименьший положительный период функции равен p:
tg (х+p)= tg х.
5.Нули функции: tg х=0 при x=pn, n
ÎZ
.
6.Промежутки знакопостоянства:
tg х>0 при xÎ (pn
; (p/2)+pn
), n
ÎZ
,
tg х<0 при xÎ ((-p/2)+pn
; pn
), n
ÎZ
.
7.Функция tg х непрерывна и дифференцируема при любом значении аргумента из области определения:
(tg х)¢ =1/cos2
x.
8.Функция tg х возрастает в каждом из промежутков ((-p/2)+pn;
(p/2)+pn
), n
ÎZ
,
Функция котангенс.
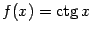 (в англоязычной литературе также (в англоязычной литературе также 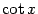 ). По определению, ). По определению, 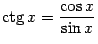 . Если . Если  ( ( 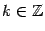 ), то ), то 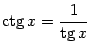 . Функция . Функция 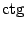 нечётна и периодична с периодом нечётна и периодична с периодом 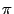 ; ;
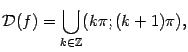
то есть 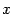 не может принимать значения вида не может принимать значения вида 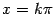 , , 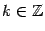 , при которых , при которых 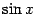 обращается в 0. обращается в 0.
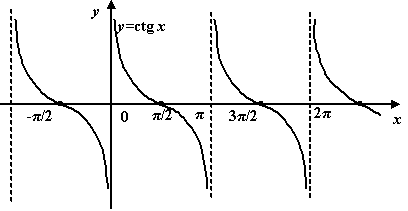
1.График функции 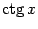 Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn
, n
ÎZ
. Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn
, n
ÎZ
.
2.Область значения – множество всех действительных чисел.
3.Функциясtg х – нечетная: сtg (-х)=- сtg х.
4.Функция сtg х – периодическая. Наименьший положительный период функции равен p:
сtg (х+p)= ctg х.
5.Нули функции: ctg х=0 при x=(p/2)+pn, n
ÎZ
.
6.Промежутки знакопостоянства:
ctg х>0 при xÎ (pn
; (p/2)+pn
), n
ÎZ
,
ctg х<0 при xÎ ((p/2)+pn
; p(n
+1)), n
ÎZ
.
7.Функция ctg х непрерывна и дифференцируема при любом значении аргумента из области определения:
(ctg х)¢ =-(1/sin2
x).
8.Функция ctg х убывает в каждом из промежутков (pn;
p(n
+1)), n
ÎZ
.
Обратные тригонометрические функции.
Это функции арксинус, арккосинус, арктангенс и арккотангенс. Они определяются как функции, обратные к главным ветвям
синуса, косинуса, тангенса и котангенса соответственно.
Arcsin x
:
1. Область определения – [-1; 1].
2. Область значений – [-П\2; п\2].
3. Монотонно возрастающая функция. (рис. 12)
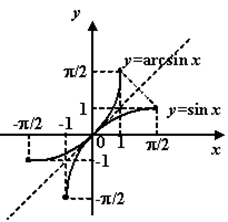
Графики главной ветви 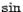 и и 
Arctg x
:
1. Область определений – R.
2. Область значений - интервал (-П\2; П\2).
3. Монотонно возрастающая функция.
4. прямые у=-П\2 и у=П\2 – горизонтальные асимптоты.(рис. 13)
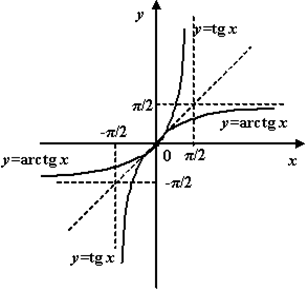
Графики главной ветви 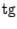 и и 
Список использованной литературы
1. Ш. А. Алимов «Алгебра», М., 1981 г.
2. А. Н. Колмогоров «Алгебра и начала анализа», М., 1991 г.
|