Равномерная непрерывность
Определение 28.7:
Функция 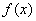 называется равномерно непрерывной на множестве называется равномерно непрерывной на множестве 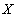 , если: , если: 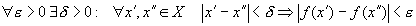 . (в отличие от критерия Коши: . (в отличие от критерия Коши: 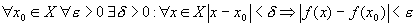 ). ).
Пояснение:
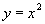 Пусть: Пусть: 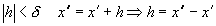 . Тогда: . Тогда: 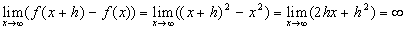 Т.е. функция Т.е. функция 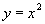 не является равномерно непрерывной на множестве не является равномерно непрерывной на множестве 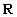 . .
Теорема 28.3:
Непрерывная на отрезке функция – равномерно непрерывна на нём.
Классы интегрируемых функций
Теорема 28.4:
Непрерывная на отрезке функция – интегрируема на нём.
Теорема 28.5:
Монотонная на отрезке функция – интегрируема на нём.
Теорема 28.5:
Если функция 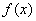 определена и ограничена на отрезке определена и ограничена на отрезке  , и если , и если 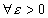 можно указать конечное число интервалов, покрывающих все точки разрыва этой функции на можно указать конечное число интервалов, покрывающих все точки разрыва этой функции на  . Причём общая длина этих интервалов меньше . Причём общая длина этих интервалов меньше 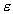 . То . То 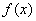 - интегрируема на - интегрируема на  . .
Замечание:
Очевидно, что если 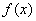 - интегрируема на - интегрируема на  , а , а 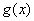 отличается от отличается от 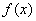 только в конечном числе точек, то только в конечном числе точек, то 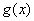 - интегрируема на - интегрируема на  и и 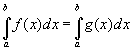 . .
Существование первообразной
Определение 28.9:
Пусть 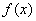 - интегрируема на - интегрируема на  , , 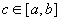 , тогда: , тогда: 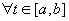 функция функция 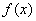 интегрируема на интегрируема на 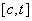 и функция и функция 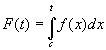 называется интегралом с переменным верхним пределом, аналогично функция называется интегралом с переменным верхним пределом, аналогично функция 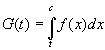 - интеграл с переменным нижним пределом. - интеграл с переменным нижним пределом.
Теорема 28.6:
Если функция 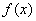 - непрерывна на - непрерывна на  , то у неё существует на , то у неё существует на  первообразная, одна из которых равна: первообразная, одна из которых равна: 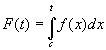 , где , где 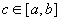 . .
Замечание 1:
Из дифференцируемости функции 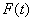 следует её непрерывность, т.е. следует её непрерывность, т.е. 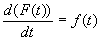
Замечание 2:
Поскольку  - одна из первообразных - одна из первообразных 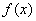 , то по определению неопределённого интеграла и теореме о разности первообразных: , то по определению неопределённого интеграла и теореме о разности первообразных:  . Это связь между определённым и неопределённым интегралами . Это связь между определённым и неопределённым интегралами
Интегрирование подстановкой
Пусть для вычисления интеграла 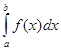 от непрерывной функции сделана подстановка от непрерывной функции сделана подстановка 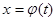 . .
Теорема.
Если 1. Функция 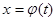 и ее производная и ее производная 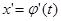 непрерывны при непрерывны при 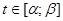
2. множеством значений функции 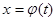 при при 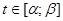 является отрезок [a;b] является отрезок [a;b]
3. 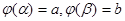 , то , то 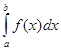 = =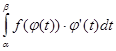 . .
Док-во:
Пусть F(x) есть первообразная для f(x) на отрезке [a;b]. Тогда по формуле Ньютона-Лейбница 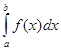 = =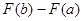 . Т.к. . Т.к. 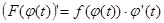 , то , то 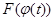 является первообразной для функции является первообразной для функции 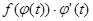 , , 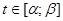 . Поэтому по формуле Ньютона-Лейбница имеем . Поэтому по формуле Ньютона-Лейбница имеем
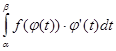 = =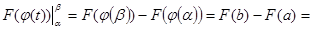 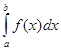 . .
Формула замены переменной в определенном интеграле.
1. при вычислении опред. интег-ла методом подстановки возвращаться к старой переменной не требуется;
2. часто вместо подстановки 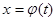 применяют подстановку t=g(x) применяют подстановку t=g(x)
3. не следует забывать менять пределы интегрирования при замене переменных.
Реклама

Интегрирование заменой переменной
.
а). Метод подведения под знак дифференциала
Пусть требуется вычислить интеграл 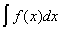 . Предположим, что существуют дифференцируемая функция . Предположим, что существуют дифференцируемая функция 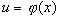 и функция и функция 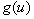 такие, что подынтегральное выражение такие, что подынтегральное выражение 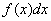 может быть записано в виде: может быть записано в виде:
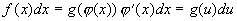 . .
Тогда: 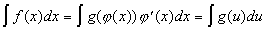 . Т.е. вычисление интеграла . Т.е. вычисление интеграла 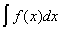 сводится к вычислению интеграла сводится к вычислению интеграла 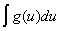 (который может оказаться проще) и последующей подстановке (который может оказаться проще) и последующей подстановке 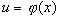 . .
Пример:
Вычислить 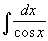 . .
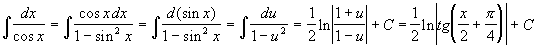 . .
Подстановка: 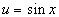 . .
б). Метод подстановки
Пусть требуется вычислить интеграл 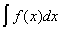 , где , где 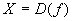 . Введём новую переменную формулой: . Введём новую переменную формулой: 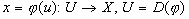 , где функция , где функция 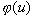 дифференцируема на дифференцируема на 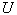 и имеет обратную и имеет обратную 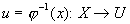 , т.е. отображение , т.е. отображение 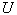 на на 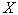 - взаимно-однозначное. Получим: - взаимно-однозначное. Получим: 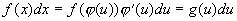 . Тогда . Тогда 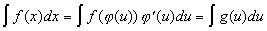 . Т.е. вычисление интеграла . Т.е. вычисление интеграла 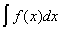 сводится к вычислению интеграла сводится к вычислению интеграла 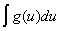 (который может оказаться проще) и последующей подстановке (который может оказаться проще) и последующей подстановке 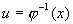 . .
Пример:
Вычислить 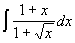 . .
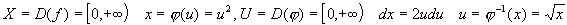 , откуда: , откуда: 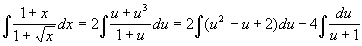 . .
Интегрирование по частям
.
Пусть 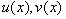 - дифференцируемые функции, тогда справедлива формула: - дифференцируемые функции, тогда справедлива формула: 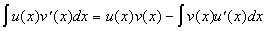 , или короче: , или короче: 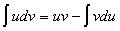 . Эта формула используется в тех случаях, когда подынтегральное выражение . Эта формула используется в тех случаях, когда подынтегральное выражение 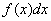 можно так представить в виде можно так представить в виде 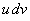 , что интеграл , что интеграл 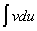 вычисляется проще исходного. вычисляется проще исходного.
Пример:
Вычислить 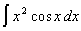 . .
Положим 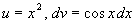 . Тогда . Тогда 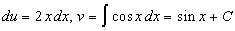 . В качестве . В качестве  выберем первообразную при выберем первообразную при 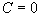 . Получим . Получим 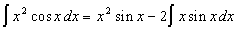 . Снова . Снова 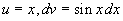 . Тогда . Тогда 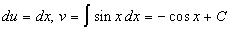 . Окончательно получим: . Окончательно получим: 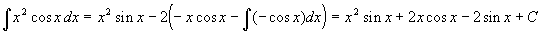 . .
Замечание 26.5:
Иногда при вычислении интеграла 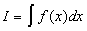 методом интегрирования по частям получается зависимость: методом интегрирования по частям получается зависимость: 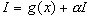 . Откуда можно получить выражение для первообразной: . Откуда можно получить выражение для первообразной: 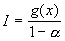 . .
Интегрирование рациональных функций
Постановка задачи:
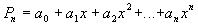 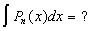 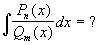
т.е. все задачи сводятся к задаче B.2).
Теорема 1:
Пусть 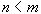 , тогда, если: , тогда, если: 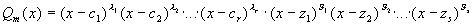 , где , где 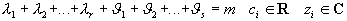 , то , то 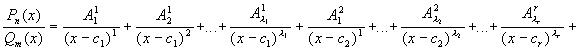 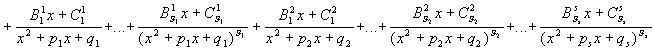 Из этой теоремы следует, что для интегрирования любой рациональной функции необходимо уметь интегрировать следующие функции: Из этой теоремы следует, что для интегрирования любой рациональной функции необходимо уметь интегрировать следующие функции:
1. 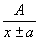 |
2. 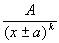 |
3. 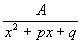 |
4. 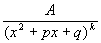 |
5. 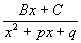 |
6. 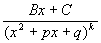 |
7. 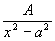 |
8. 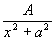 |
9. 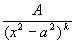 |
10. 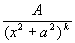 . . |
Интегрирования дробно-линейных и квадратичных иррациональностей
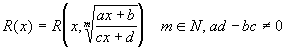
Сделав подстановку: 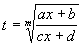 , получим: , получим: 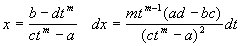 . .
тогда 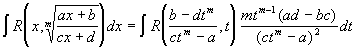
a). Подстановки Эйлера.
1). Корни многочлена 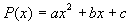 - комплексные, сделав подстановку: - комплексные, сделав подстановку: 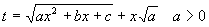 , получим: , получим: 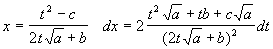 . .
2). Корни многочлена 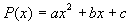 - действительные: - действительные: 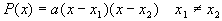 . Подстановка: . Подстановка: 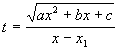 , получаем: , получаем: 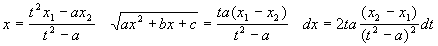 . .
b). Подстановка: 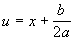 , далее, если: , далее, если:
1).  подстановка - подстановка - 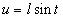 |
2). 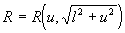 подстановка - подстановка - 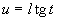 |
3). 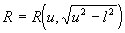 подстановка - подстановка - 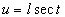 |
c).
Если 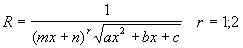 подстановка - подстановка - 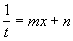
Интегрирование функций, рационально зависящих от тригонометрических
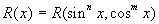
Универсальная подстановка: 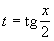 , тогда: , тогда: 
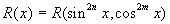 подстановка: подстановка: 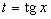
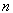 или или 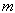 - нечётные: вносим функцию при нечётной степени под знак дифференциала - нечётные: вносим функцию при нечётной степени под знак дифференциала
Интегрируется по частям
Неопределенный интеграл
Определение 26.1:
Функция 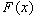 называется первообразной для функции называется первообразной для функции  на на 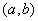 , если: , если: 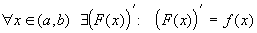 . .
Пусть 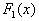 и и 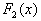 - первообразные функции - первообразные функции  на на 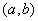 . Тогда: . Тогда: 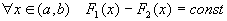 . .
Определение 26.2:
Неопределённым интегралом от функции  на на 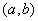 называется объединение всех первообразных называется объединение всех первообразных  на этом интервале. Обозначается: на этом интервале. Обозначается: 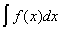 . .
Замечание 26.1:
Если 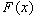 - одна из первообразных - одна из первообразных  на на 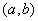 , то , то 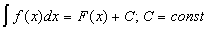 . .
Замечание 26.2:
Подынтегральное выражение в определении представляет из себя полный дифференциал первообразной 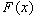 на на 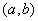 , т.е. , т.е. 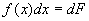 . .
Замечание 26.3:
Два неопределённых интеграла равны “с точностью до постоянной”.
Реклама

Св-ва неопределенного интеграла:
1.Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопред. интегр. равна подынтегр. функции. Благодаря этому св-ву правильность интегрирования проверяется дифференцированием.
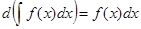 , , 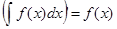
2. Неопред. интегр. от дифференциала нек-рой функции равен сумме этой функции и производной постоянной:
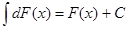
3. Постоянный множитель м. выносить за знак интеграла:
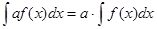 , где a , где a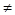 0-постоянная. 0-постоянная.
4. Неопред. интегр. от алгебраич. суммы конечного числа непрерывных функций равен алгебраич. сумме интегралов от слагаемых функций:
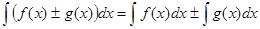
5. (Инвариантность формулы интегрирования). Если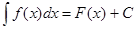 , то и , то и 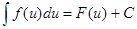 , где u= , где u=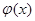 - произвольн. функция, имеющая непрерывную производную. - произвольн. функция, имеющая непрерывную производную.
Табличные интегралы
Определённый интеграл.
Интегрируемость
Определение 28.1:
Множество точек отрезка  таких, что: таких, что: 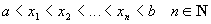 называют разбиением отрезка называют разбиением отрезка  . Длины частичных отрезков разбиения обозначим: . Длины частичных отрезков разбиения обозначим: 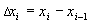 . Мелкостью разбиения . Мелкостью разбиения 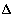 (читается – “дельта большое”) назовем максимальнуя из длин отрезков разбиения, т.е. (читается – “дельта большое”) назовем максимальнуя из длин отрезков разбиения, т.е. 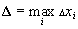 . .
Определение 28.2:
Пусть в определении 28.1 для всех 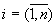 точки точки 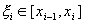 . Интегральной суммой функции . Интегральной суммой функции  на отрезке на отрезке  с разбиением с разбиением 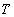 будем называть сумму (зависящую от разбиения будем называть сумму (зависящую от разбиения 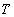 и выбора точек и выбора точек 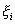 ) вида: ) вида:  . .
Определение 28.3:
Пределом интегральных сумм функции 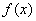 на отрезке на отрезке  назовём такое число назовём такое число 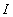 , что , что 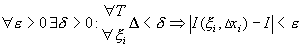 . Обозначается: . Обозначается: 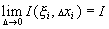 . . 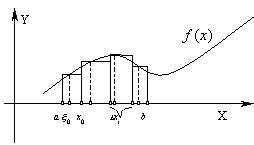
Определение 28.4:
Функция 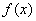 называется интегрируемой на отрезке называется интегрируемой на отрезке  , если существует конечный предел её интегнральных сумм на , если существует конечный предел её интегнральных сумм на  . Обозначается: . Обозначается: 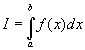 . .
Теорема 28.1:
Если 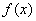 интегрируема на отрезке интегрируема на отрезке  , то она ограничена на нём. , то она ограничена на нём.
Замечание 1:
Эта теорема является необходимым, но недостаточным условием интегрируемости функции. Пример – функция Дирихле (ограничена, но неинтегрируема).
Критерий интегрируемости функций
Теорема 28.2:
Для того, чтобы ограниченная на некотором отрезке функция, была интегрируема на нём, необходимо и достаточно, чтобы выполнялось условие: 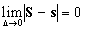 . .
Следствие 1:
Условие Т.2 эквивалентно условию: 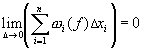 . .
Следствие 2:
Если функция интегрируема на , то: 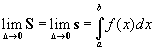 . .
Определение 28.8:
Определённым интегралом функции 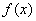 на на  называется число называется число 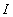 , равное пределу интегральных сумм , равное пределу интегральных сумм 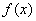 на на  . Условие интегрируемости эквивалентно существованию определённого интеграла. . Условие интегрируемости эквивалентно существованию определённого интеграла.
Свойства определённого интеграла
1. Если с
– постоянное число и функция f(x) интегрируема на [a;b], то 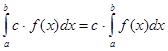 , т.е. пост. множитель с
можно выносить за знак определенного интег-ла. , т.е. пост. множитель с
можно выносить за знак определенного интег-ла.
2. Если функции f(x), g(x) интегрируемы на [a;b], тогда интегрируема на [a;b] их сумма и разность
 , , 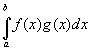
3. Если 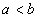 , то: , то: 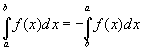
4. Если функция f(x) интегрируема на [a;b] и a<c<b, то
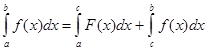 , т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это св-во наз-ют аддивностью
определенного интеграла. , т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это св-во наз-ют аддивностью
определенного интеграла.
Сравнение определённых интегралов
Если 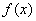 - интегрируема на - интегрируема на  и и 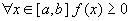 , то: , то: 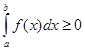 . .
Если 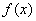 - интегрируема на - интегрируема на  и и 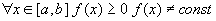 , то: , то: 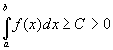
Неравенство м\у непрерывными функциями на отрезке [a;b], можно интегрировать. Если 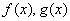 - интегрируемы на - интегрируемы на  и почти для всех и почти для всех 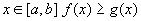 , то: , то: 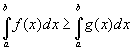
Модуль определенного интег-ла не превосходит интег-ла от модуля подынтегральной функции. Если 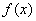 - интегрируема на - интегрируема на  , то , то 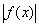 - также интегрируема на - также интегрируема на  (обратное неверно), причём: (обратное неверно), причём: 
Оценка интеграла. Если m и M-соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке [a;b]. Если 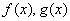 - интегрируемы на - интегрируемы на  и и 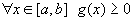 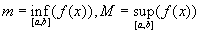 , то: , то: 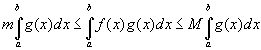
Теорема о среднем значении
Если функция f(x) непрерывна на отрезке [a;b], то существует точка 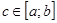 такая, что такая, что 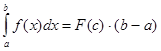 . .
Док-во: По формуле Ньютона-Лейбница имеем
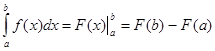 , где F’(x)=f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F’(c)*(b-a)=f(c)*(b-a). , где F’(x)=f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F’(c)*(b-a)=f(c)*(b-a).
Эта теорема при f(x)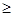 0 имеет простой геометрич. смысл: значение определенного интег-ла равно, при нек-ром 0 имеет простой геометрич. смысл: значение определенного интег-ла равно, при нек-ром 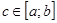 , площади прямоугольника с высотой f(с) и основанием b-a. , площади прямоугольника с высотой f(с) и основанием b-a.
Число 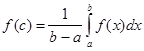 наз-ся средним значением
функции f(x) на отрезке [a;b]. наз-ся средним значением
функции f(x) на отрезке [a;b].
Формула Ньютона-Лейбница
Если 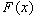 - первообразная непрерывной функции - первообразная непрерывной функции  на на 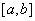 , то: , то: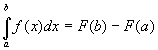 . .
Док-во: Рассмотрим тождество
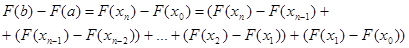
Преобразуем каждую разность в скобках по формуле Лагранжа
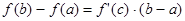 . Получим . Получим 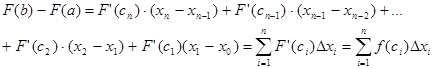 т.е. т.е. 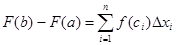 , где , где 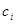 есть нек-рая точка интервала есть нек-рая точка интервала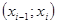 . Т.к. функция y=f(x) непрерывна на [a;b]. Поэтому существует предел интегральной суммы, равный определенному интегралу от f(x) на [a;b]. . Т.к. функция y=f(x) непрерывна на [a;b]. Поэтому существует предел интегральной суммы, равный определенному интегралу от f(x) на [a;b].
Переходя к пределу при 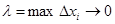 , получаем F(b)-F(a)= , получаем F(b)-F(a)=
=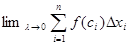 , т.е. , т.е. 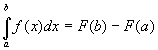 . .
интеграл с переменным верхним пределом
Если изменять, например, верхний предел так, чтобы не выйти за пределы отрезка [a;b], то величина интеграла будет изменяться. Другими словами, интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела. Производная определенного интег-ла по переменному верхнему пределу равна подынтегральной функции, в к-рой переменная интегрирования заменена этим пределом, т.е.
 . .
Док-во: По формуле Ньютона-Лейбница имеем: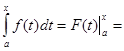 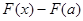 . .
Следовательно, 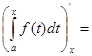
=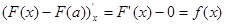 . .
Это значит, что определенный интег-л с переменным верхним пределом есть одна из первообразных подынтегральной функции.
|