КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ
Общее число неповторяющихся сообщений, которое может быть составлено из алфавита m
путем комбинирования по n
символов в сообщении,
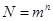 . (1) . (1)
Неопределенность, приходящаяся на символ первичного (кодируемого)[1]
алфавита, составленного из равновероятностных и взаимонезависимых символов,
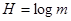 . (2) . (2)
Основание логарифма влияет лишь на удобство вычисления. В случае оценки энтропии:
а) в двоичных единицах
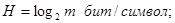
б) в десятичных единицах
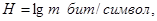
где 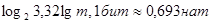 ; ;
в) в натуральных единицах
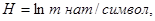
где 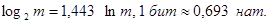
Так как информация есть неопределенность, снимаемая при получении сообщения, то количество информации может быть представлено как произведение общего числа сообщений к
на среднюю энтропию Н
, приходящуюся на одно сообщение:
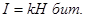 (3) (3)
Для случаев равновероятностных и взаимонензависимых символов первичного алфавита количество информации в к
сообщениях алфавита m
равно
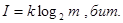
а количество информации в сообщении, составленном из к
неравновероятностных символов,
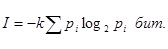 (5) (5)
Для неравновероятностных алфавитов энтропия на символ алфавита
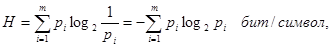 (4) (4)
При решении задач, в которых энтропия вычисляется как сумма произведений вероятностей на их логарифм, независимо от того, являются ли они безусловными 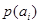 , условными , условными 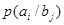 или вероятностями совместных событий или вероятностями совместных событий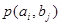 . .
Количество информации определяется исключительно характеристиками первичного алфавита, объем – характеристиками вторичного алфавита. Объем[2]
информации
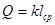 (6) (6)
где l
ср
– средняя длина кодовых слов вторичного алфавита. Для равномерных кодов (все комбинации кода содержат одинаковое количество разрядов)
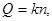
где n
– длина кода (число элементарных посылок в коде). Согласно (3), объем равен количеству информации, если l
ср
=Н
, т.е. в случае максимальной информационной нагрузки на символ сообщения. Во всех остальных случаях 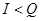 . .
Например, если кодировать в коде Бодо некоторые равновероятный алфавит, состоящий из 32 символов, то
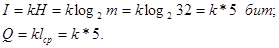
Если закодировать в коде Бодо русский 32-буквенный алфавит, то без учета корреляции между буквами количество информации
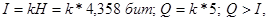
т.е. если в коде существует избыточность и 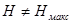 , то объем в битах всегда больше количества информации в тех же единицах. , то объем в битах всегда больше количества информации в тех же единицах.
Тема 2. Условная энтропия и энтропия объединения
Понятие условной энтропии в теории информации используется при определении взаимозависимости[3]
между символами кодируемого алфавита, для определения потерь при передаче информации по каналам связи, при вычислении энтропии объединения.
Реклама

Во всех случаях при вычислении условной энтропии в том или ином виде используются условные вероятности.
Если при передаче n
сообщений символ А
появился m
раз, символ В
появился l
раз, а символ А
вместе с символом В
– к
раз, то вероятность появления символа А
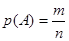 ; вероятность появления символа В ; вероятность появления символа В
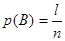 ; вероятность совместного появления символов А
и В ; вероятность совместного появления символов А
и В
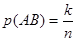 ; условная вероятность появления символа А
относительно символа В
и условная вероятность появления символа В
относительно символа А ; условная вероятность появления символа А
относительно символа В
и условная вероятность появления символа В
относительно символа А
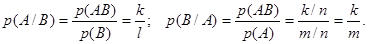 (7) (7)
Если известна условная вероятность, то можно легко определить и вероятность совместного появления символов А
и В
, используя выражения (7)
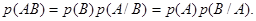 (8) (8)
От классического выражения (4) формула условной энтропии отличается тем, что в ней вероятности – условные:
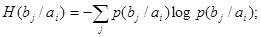 (9) (9)
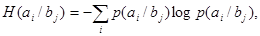 (10) (10)
где индекс i
выбран для характеристики произвольного состояния источника сообщения А, индекс j выбран для характеристики произвольного состояния адресата В.
Различают понятия частной и общей условной энтропии. Выражение (9) и (10) представляют собой частные условные энтропии.
Общая условная энтропия
сообщения В относительно сообщения А характеризует количество информации, содержащейся в любом символе алфавита, и определяется усреднением по всем символам, т. е. по всем состояниям с учетом вероятности появления каждого из состояний, и равна сумме вероятностей появления символов алфавита на неопределенность, которая остается после того, как адресат принял сигнал
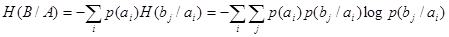 (11) (11)
Выражение (11) является общим выражением для определения количества информации на один символ сообщения для случая неравномерных и взаимонезависимых символов.
Так как 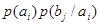 представляет собой вероятность совместного появления двух событий представляет собой вероятность совместного появления двух событий 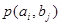 , то формула (11) можно записать следующим образом: , то формула (11) можно записать следующим образом:
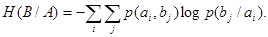 (12) (12)
Понятие общей и частной условной энтропии широко используется при вычислении информационных потерь в каналах связи с шумами.
В общем случае, если мы передаем m
сигналов А
и ожидаем получить m
сигналов В
, влияние помех в канале связи полностью описывается канальной матрицей
, которую мы приводим ниже:

В
А
|
b1
b2
… bj
… bm
|
а1
а2
…
аi
…
аm
|
 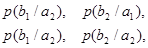 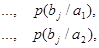  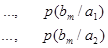
…………………………………………………………..
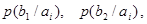 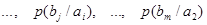
……………………………………………………………
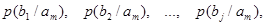 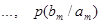
|
Вероятности, которые расположены по диагонали, определяют правильный прем, остальные – ложный. Значение цифр, заполняющих колонки канальной матрицы, обычно уменьшаются по мере удаления от главной диагонали и при полном отсутствии помех всех, кроме цифр, расположенных на главной диагонали, равны нулю.
Если описывать канал связи со стороны источника сообщений, то прохождение данного вида сигнала в данном канале связи описывается распределением условных вероятностей вида 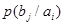 , так для сигнала , так для сигнала 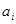 распределением вида распределением вида
Реклама

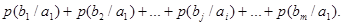 (13) (13)
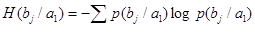 (14) (14)
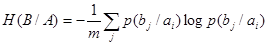 (15) (15)
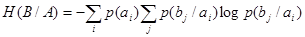 (16) (16)
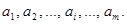
В
А
|
b1
b2
… bj
… bm
|
а1
а2
…
аi
…
аm
|
 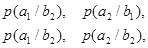 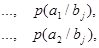  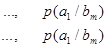
…………………………………………………………..
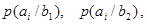 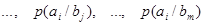
……………………………………………………………
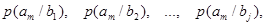 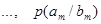
|
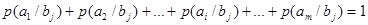
 (17) (17)
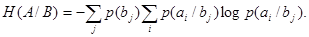 (18) (18)
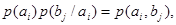
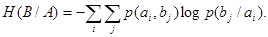 (19) (19)
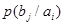
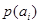
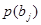
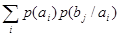
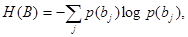
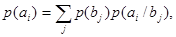
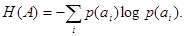
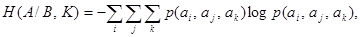
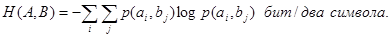
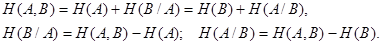
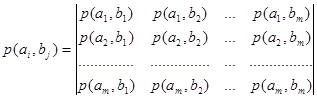
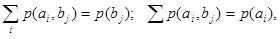
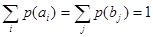
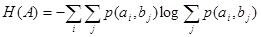
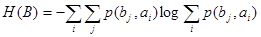
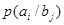 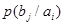
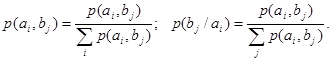
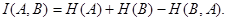
тема 3. Вычисление информационных потерь при передаче сообщений по каналам связи с шумами
Потери информации в каналах связи с шумами обычно описывают при помощи условной энтропии и энтропии объединения.
Если помех нет или их уровень настолько низок, что они не в состоянии уничтожить сигнал или имитировать полезный сигнал в отсутствие передачи, то при передаче мы будем твердо уверены, что получим - сигнал, соответствующий переданному ai
-му сигналу. События А и В статистически жестко связаны, условная вероятность максимальна , а условная энтропия
!!!!1
так как !!!!. В этом случаи количество информации, содержащейся в принятом ансамбле сообщений В, равно энтропии передаваемых сообщений ансамбля А, т.е. I(В, А) = Н (А).
При высоком уровне помех любой из принятых сигналов bj
может соответствовать любому принятому сигналу ai
, статистическая связь между переданными и принятыми сигналами отсутствует. В этом случае вероятности!!!!!! Есть вероятности независимых событий и !!!!!!
!!!!1
так как !!11, т.е. условная энтропия равна безусловной, а количество информации, содержащейся в В, относительно А равно нулю:
!!!!
Информационные характеристики реальных каналов связи лежат между этими двумя предельными случаями. При этом потери информации при передаче !! символов по данному каналу связи
!!!!!
Несмотря на то, что часть информации поражается помехами, между принятыми и переданными сообщениями существует статистическая зависимость. Это позволяет описывать информационные характеристики реальных каналов связи при помощи энтропии объединения статистически зависимых событий. Так как
!!!!1
то потери в канале связи могут быть учтены при помощи энтропии объединения следующим образом:
!!1!
а с использованием условной энтропии
!!!
Для вычисления среднего количества информации, содержащегося в принятом ансамбле сообщений В относительно передаваемого ансамбля сообщений А в условиях действия помех, пользуются следующими выражениями, выведенными непосредственно из выражения (25):
!!!!!!!!
Для вычисления часто удобно применять выражения (26-28) в виде
!!!!!!!
Для полного и всестороннего описания канала связи необходимо задать: канальную матрицу вида !!!!!! и безусловные вероятности вида !!!! или канальную матрицу вида !!!!!! и безусловные вероятности вида !!!!!. В последнем случае сумма значений матрицы по столбцам дает безусловные вероятности вида !!!!!!!!!!, а сумма по строкам дает безусловные вероятности вида !!!!!!. Условные вероятности могут быть найденными из выражений:
!!!!!!!
Зная условные и безусловные вероятности, можно найти Н (А), Н(В), Н(А/В) и Н(В/А).
Если уровень помех настолько высок, что с равной вероятностью можно ожидать переход любого символа источника сообщения в произвольный символ первичного алфавита,. то энтропия канала связи будет равна !!!!!, а количество информации !!!!!!!, при этом значение I может быть отрицательной величиной, что означает, что канал связи вносит дезинформацию.
ТЕМА 5. ОПРЕДЕЛЕНИЕ ИЗБЫТОЧНОСТИ СООБЩЕНИЙ. ОПТИМАЛЬНОЕ КОДИРОВАНИЕ
Если энтропия источника сообщений не равна максимальной энтропии для алфавита с данным количеством качественных признаков (имеются в виду качественные признаки алфавита, при помощи которых составляются сообщения), то это прежде всего означает, что сообщения данного источника могли бы нести большее количество информации. Абсолютная
недогруженность на символ сообщений такого источника
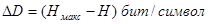
Для определения количества «лишней» информации, которая заложена в структуре алфавита либо в природе кода, вводится понятие избыточности.
Избыточность, с которой мы имеем дело в теории информации, не зависит от содержания сообщения и обычно заранее известна из статистических данных[4]
. Информационная избыточность
показывает относительную
недогруженность на символ алфавита и является безразмерной величиной:
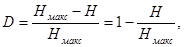 (45) (45)
где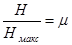 —
коэффициент сжатия (относительная энтропия). —
коэффициент сжатия (относительная энтропия).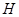 и и 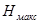 берутся относительно одного и того же алфавита. берутся относительно одного и того же алфавита.
Кроме общего понятия избыточности существуют частные виды избыточности.
Избыточность, обусловленная неравновероятным распределением символов в сообщении,
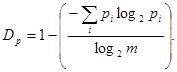 (46) (46)
Избыточность, вызванная статистической связью между символами сообщения,
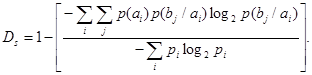 (47) (47)
Полная информационная избыточность
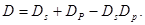 (48) (48)
Избыточность, которая заложена в природе данного кода,
получается в результате неравномерного распределения в сообщениях качественных признаков этого кода и не может быть задана одной цифрой на основании статистических испытаний.
Так при передаче десятичных цифр двоичным кодом максимально загруженными бывают только те символы вторичного алфавита, которые передают значения, являющиеся целочисленными степенями двойки. В остальных случаях тем же количеством символов может быть передано большее количество цифр (сообщений). Например, тремя двоичными разрядами мы можем передать и цифру 5, и цифру 8, т. е. на передачу пяти сообщений тратится столько же символов, сколько тратится и на восемь сообщений.
Фактически для передачи сообщения достаточно иметь длину кодовой комбинации
 , ,
где N -
общее количество передаваемых сообщений.
L можно представить и как
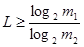 , ,
где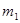 и и 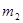 —соответственно качественные признаки первичного и вторичного алфавитов. Поэтому для цифры 5 в двоичном коде можно записать —соответственно качественные признаки первичного и вторичного алфавитов. Поэтому для цифры 5 в двоичном коде можно записать
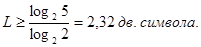
Однако эту цифру необходимо округлить
до ближайшего целого числа, так как длина кода не может быть выражена дробным числом. Округление, естественно, производится в большую сторону. В общем случае, избыточность от округления
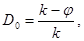
где 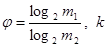 —
округленное до ближайшего целого числа значение —
округленное до ближайшего целого числа значение  . Для нашего примера . Для нашего примера
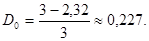
Избыточность — не всегда нежелательное явление. Для повышения помехоустойчивости кодов избыточность необходима и ее вводят искусственно в виде добавочных  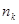 символов (см. тему 6). Если в коде всего п
разрядов и символов (см. тему 6). Если в коде всего п
разрядов и 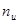 из них несут информационную нагрузку, то из них несут информационную нагрузку, то 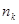 = =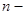 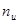 характеризует абсолютную корректирующую избыточность,
а величина характеризует абсолютную корректирующую избыточность,
а величина 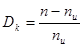 характеризует относительную
корректирующую избыточность. характеризует относительную
корректирующую избыточность.
Информационная избыточность - обычно явление естественное, заложена она в первичном алфавите. Корректирующая избыточность - явление искусственное, заложена онав кодах,
представленных во вторичном алфавите.
Наиболее эффективным способом уменьшения избыточности сообщения является построение оптимальных кодов.
Оптимальные коды[5]
-
коды с практически нулевой избыточностью. Оптимальные коды имеют минимальную среднюю длину кодовых слов - L. Верхняя и нижняя границыL
определяютсяиз неравенства
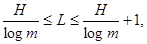 (49) (49)
где Н -
энтропия первичного алфавита, т -
число качественных признаков вторичного алфавита.
В случае поблочного кодирования, где каждый из блоков состоит из М
независимых букв 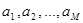 ,
минимальная средняя длина кодового блока лежит в пределах ,
минимальная средняя длина кодового блока лежит в пределах
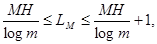 (50) (50)
Общее выражение среднего числа элементарных символов на букву сообщения при блочном кодировании
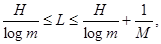 (51) (51)
С точки зрения информационной нагрузки на символ сообщения поблочное кодирование всегда выгоднее, чем побуквенное.
Суть блочного кодирования можно уяснить на примере представления десятичных цифр в двоичном коде. Так, при передаче цифры 9 в двоичном коде необходимо затратить 4 символа, т. е. 1001. Для передачи цифры 99 при побуквенном кодировании - 8, при поблочном - 7, так как 7 двоичных знаков достаточно для передачи любой цифры от 0 до 123; при передаче цифры 999 соотношение будет 12 - 10, при передаче цифры 9999 соотношение будет 16 - 13 и т. д. В общем случае «выгода» блочного кодирования получается и за счет того, что в блоках происходит выравнивание вероятностей отдельных символов, что ведет к повышению информационной нагрузки на символ.
При построении оптимальных кодов наибольшее распространение нашли методики Шеннона—Фано и Хаффмена.
Согласно методике Шеннона - Фано построение оптимального кода ансамбля из сообщений сводится к следующему:
1-й шаг. Множество из сообщений располагается в порядке убывания вероятностей.
2-й шаг. Первоначальный ансамбль кодируемых сигналов разбивается на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны. Если равной вероятности в подгруппах нельзя достичь, то их делят так, чтобы в верхней части (верхней подгруппе) оставались символы, суммарная вероятность которых меньше суммарной вероятности символов в нижней части (в нижней подгруппе).
3-й шаг. Первой группе присваивается символ 0, второй группе символ 1.
4-й шаг. Каждую из образованных подгрупп делят на две части таким образом, чтобы суммарные вероятности вновь образованных подгрупп были по возможности равны.
5-й шаг. Первым группам каждой из подгрупп вновь присваивается 0, а вторым - 1. Таким образом, мы получаем вторые цифры кода. Затем каждая из четырех групп вновь делится на равные (с точки зрения суммарной вероятности) части до тех пор, пока в каждой из подгрупп не останется по одной букве.
Согласно методике Хаффмена, для построения оптимального кода N
символы первичного алфавита выписываются в порядке убывания вероятностей. Последние 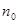 символов, где символов, где 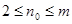 [6]
и [6]
и 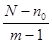 - целое число, объединяют в некоторый новый символ с вероятностью, равной сумме вероятностей объединенных символов Последние символы с учетом образованного символа вновь объединяют, получают новый, вспомогательный символ, опять выписывают символы в порядке убывания вероятностей с учетом вспомогательного символа и т. д. до тех пор, пока сумма вероятностей т
оставшихся символов после - целое число, объединяют в некоторый новый символ с вероятностью, равной сумме вероятностей объединенных символов Последние символы с учетом образованного символа вновь объединяют, получают новый, вспомогательный символ, опять выписывают символы в порядке убывания вероятностей с учетом вспомогательного символа и т. д. до тех пор, пока сумма вероятностей т
оставшихся символов после 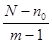 -го выписывания в порядке убывания вероятностей не даст в сумме вероятность, равную 1. На практике обычно, не производят многократного выписывания вероятностей символов с учетом вероятности вспомогательного символа, а обходятся элементарными геометрическими построениями, суть которых сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность. Затем с учетом вновь образованных символов, которым присваивается значение суммарной вероятности двух предыдущих, строят кодовое дерево, в вершине которого стоит символ с вероятностью 1. При этом отпадает необходимость в упорядочивании символов кодируемого алфавита в порядке убывания вероятностей. -го выписывания в порядке убывания вероятностей не даст в сумме вероятность, равную 1. На практике обычно, не производят многократного выписывания вероятностей символов с учетом вероятности вспомогательного символа, а обходятся элементарными геометрическими построениями, суть которых сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность. Затем с учетом вновь образованных символов, которым присваивается значение суммарной вероятности двух предыдущих, строят кодовое дерево, в вершине которого стоит символ с вероятностью 1. При этом отпадает необходимость в упорядочивании символов кодируемого алфавита в порядке убывания вероятностей.
Построенные по указанным выше (либо подобным) методикам коды с неравномерным распределением символов, имеющие минимальную среднюю длину кодового слова, называют оптимальным, неравномерным, кодами
(ОНК). Равномерные коды могут быть оптимальными только для передачи сообщений с равновероятным распределением символов первичного алфавита, при этом число символов первичного алфавита должно быть равно целой степени числа, равного количеству качественных признаков вторичного алфавита, а в случае двоичных кодов - целой степени двух.
Максимально эффективными будут те ОНК, у которых
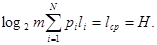
Для двоичных кодов
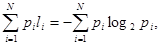 (52) (52)
так как log2
2 = 1. Очевидно, что равенство (52) удовлетворяется при условии, что длина кода во вторичном алфавите
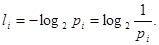
Величина 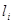 точно равна Н,
если точно равна Н,
если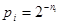 , где п -
любое целое число. Если п
не является целым числом для всех значений букв первичного алфавита, то , где п -
любое целое число. Если п
не является целым числом для всех значений букв первичного алфавита, то 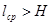 и, согласно основной теореме кодирования[7]
, средняя длина кодового слова приближается к энтропии источника сообщений по мере укрупнения кодируемых блоков. и, согласно основной теореме кодирования[7]
, средняя длина кодового слова приближается к энтропии источника сообщений по мере укрупнения кодируемых блоков.
Эффективность ОНК. оценивают при помощи коэффициента статистического сжатия:
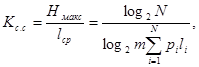 (53) (53)
который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением методов нестатистического кодирования и коэффициента относительной эффективности
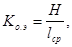 (54) (54)
который показывает, насколько используется статистическая избыточность передаваемого сообщения.
Для наиболее общего случая неравновероятных и взаимонезависимых символов
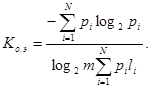
Для случая неравновероятных и взаимозависимых символов
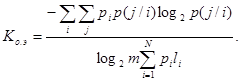
ТЕМА 6. ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК В СООБЩЕНИЯХ
Понятие об идее коррекции ошибок
Для того чтобы в принятом сообщении можно было обнаружить ошибку это сообщение должно обладать некоторой избыточной информацией, позволяющей отличить ошибочный код от правильного Например, если переданное сообщение состоит из трех абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:
10110 - переданная кодовая комбинация;
10010 -
1-я принятая комбинация;
10100 - -я принятая комбинация;
00110 - 3-я принятая комбинация;
10110 - накопленная комбинация.
Как видим, несмотря на то, что во всех трех принятыхкомбинациях были ошибки, накопленная не содержит ошибок[8]
.
Принятое сообщение может также состоять из кода и его инверсии. Код и инверсия посылаются в канал связи как одно целое. Ошибка на приемном конце выделяется при сопоставлении кода и его инверсии.
Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации, необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом.
Для двоичных кодов число кодовых комбинаций в кодах с постоянным весом длиной в п
символов равно
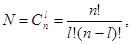 (55) (55)
где 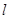 - число единиц в кодовом слове. Если бы не существовало условия постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно - число единиц в кодовом слове. Если бы не существовало условия постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 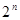 . Примером кода с постоянным весом может служить стандартный телеграфный код № 3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течение которых должна быть принята одна кодовая комбинация, всегда приходятся три токовые и четыре безтоковые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибки. . Примером кода с постоянным весом может служить стандартный телеграфный код № 3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течение которых должна быть принята одна кодовая комбинация, всегда приходятся три токовые и четыре безтоковые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибки.
Еще одним примером введения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их всегда. была четной или нечетной. Сбой любого одного символа всегда нарушит условие четности (нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах, т. е. ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот).
Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бьг не многократное повторение одного и того же кода, не добавление к коду его инверсии, не несущей никакой информации, если бы. не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходится вводить для того, чтобы можно было отличить ошибочную комбинацию от правильной.
Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут[9]
.
Минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга, называется кодовым расстоянием.
Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называется минимальным кодовым расстоянием.
Минимальное кодовое расстояние - параметр, определяющий помехоустойчивость кода и заложенную в коде избыточность. Минимальным кодовым расстоянием определяются корректирующие свойства кодов.
В общем случае для обнаружения r
ошибок минимальное кодовое расстояние
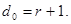 (56) (56)
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
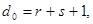 (57) (57)
где s - число исправляемых ошибок.
Для кодов, только исправляющих ошибки,
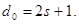 (58) (58)
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и подсчитать число единиц в полученной комбинации.
Понятие кодового расстояния хорошо усваивается на примере построения геометрических моделей кодов. На геометрических моделях в вершинах n-угольников, где n-значность кода, расположены кодовые комбинации, а количество ребер n-угольника, отделяющих одну комбинацию от другой, равно кодовому расстоянию.
Если кодовая комбинация двоичного кода А
отстоит от кодовой комбинации В
на расстоянии d
,
то это значит, что в коде А
нужноd
символов заменить на обратные, чтобы получить код В,
но это не означает, что нужно d
добавочных символов, чтобы кодобладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимальное кодовое расстояние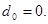
Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов 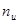 и числом корректирующих разрядов и числом корректирующих разрядов 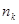 должно удовлетворять следующим условиям: должно удовлетворять следующим условиям:
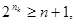 (59) (59)
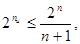 60) 60)
при этом подразумевается, что общая длина кодовой комбинации
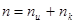 . (61) . (61)
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием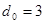 удобно пользоваться выражениями: удобно пользоваться выражениями:
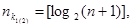 (62) (62)
если известна длина полной кодовой комбинации п,
и
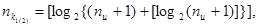 (63) (63)
если при расчетах удобнее исходить из заданного числа информационных символов 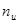 [10]
. [10]
.
Для кодов, обнаруживающих все трехкратные ошибки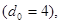
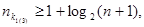 (64) (64)
или
 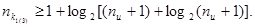 (65) (65)
Для кодов длиной в п
символов, исправляющих одну или две ошибки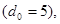
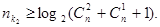 (66) (66)
Для практических расчетов можно пользоваться выражением
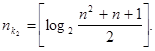 (67) (67)
Для кодов, исправляющих 3 ошибки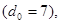
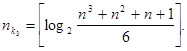 (68) (68)
Для кодов, исправляющих s ошибок 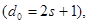
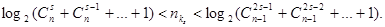 (69) (69)
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильберта [3][11]
Для приближенных расчетов можно пользоваться выражением
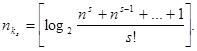 (70) (70)
Можно предположить, что значение 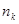 будет приближаться к верхней границе в зависимости от того, насколько выражение под знаком логарифма приближается к целой степени двух. будет приближаться к верхней границе в зависимости от того, насколько выражение под знаком логарифма приближается к целой степени двух.
Линейные групповые коды
Линейными
называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Правила сложения по модулю 2 определяются следующими равенствами:
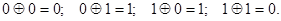
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.
Свойство линейных кодов:
сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.
Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами.
Свойство группового кода:
минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора
(кодовой комбинации) равен числу его ненулевых компонентов.
Расстояние между двумя кодовыми векторами
равно весу вектора, полученного в результате сложения исходных векторов помодулю 2. Таким образом, для данного группового кода
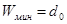 . .
Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода 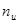 и и 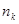 .
Число строк матрицы равно .
Число строк матрицы равно 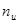 , число столбцов равно , число столбцов равно 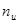 + +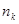 = =
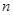 : :
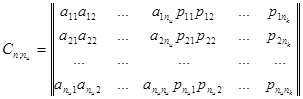 (71) (71)
Коды, порождаемые этими матрицами, известны как 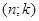 -коды,
где -коды,
где 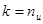 ,
а соответствующие им матрицы называют порождающими, производящими, образующими. ,
а соответствующие им матрицы называют порождающими, производящими, образующими.
Порождающая матрица С
может быть представлена двумя матрицами И и П (информационной и проверочной). Число столбцов матрицы П равно 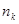 ,
число столбцов матрицы И равно ,
число столбцов матрицы И равно 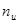 : :
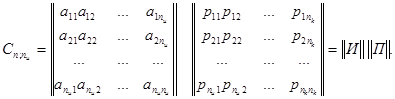 (72) (72)
Теорией и практикой установлено, что в качестве матрицы И удобно брать единичную матрицу в канонической форме:
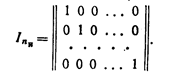
При выборе матрицы П исходят из следующих соображений:чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному[12]
, с другой стороны, число единиц в матрице П определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, т. е. чем больше единиц в матрице П, тем сложнее аппаратура.
Вес каждой строки матрицы П должен быть не менее 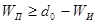 ,
где ,
где 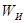 - вес соответствующей строки матрицы И. Если матрица И - единичная, то - вес соответствующей строки матрицы И. Если матрица И - единичная, то (удобство выбора в качестве матрицы И единичной матрицы очевидно: при (удобство выбора в качестве матрицы И единичной матрицы очевидно: при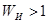 усложнилось бы как построение кодов, так и их техническая реализация). усложнилось бы как построение кодов, так и их техническая реализация).
При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:
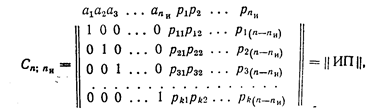
называемому левой канонической формой порождающей матрицы.
Для кодов с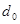 =2 производящая матрица С
имеет вид =2 производящая матрица С
имеет вид
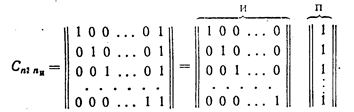
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.
Для кодов с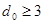 порождающая матрица не может быть представлена в форме, общей для всех кодов с данным порождающая матрица не может быть представлена в форме, общей для всех кодов с данным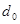 .
Вид матрицы зависит от конкретных требований к порождаемому коду. Этими требованиями могут быть либо минимум корректирующих разрядов, либо максимальная простота аппаратуры. .
Вид матрицы зависит от конкретных требований к порождаемому коду. Этими требованиями могут быть либо минимум корректирующих разрядов, либо максимальная простота аппаратуры.
Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными
или совершенными кодами.
Для кодов с соотношения п
и соотношения п
и 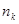 .
следующие: (3; 1), (7;4), (15; 11), (31; 26), (63; 57) и т. д. .
следующие: (3; 1), (7;4), (15; 11), (31; 26), (63; 57) и т. д.
Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью r + 1; r + 2 и т. д. и имеющие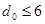 и и 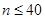 , были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь комбинации с максимальным весом. Для этого при построении кодов с , были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь комбинации с максимальным весом. Для этого при построении кодов с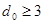 последовательно используются векторы длиной п последовательно используются векторы длиной п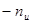 , весом
, весом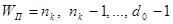 . Тем же Слепяном в работе [11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность.
Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом . Тем же Слепяном в работе [11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность.
Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом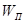 = 2, 3, ..., = 2, 3, ...,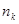 . Если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяющих условию . Если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяющих условию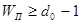 , больше , больше 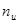 ,
то в первом случаене используют наборы с наименьшим весом, а во втором - с наибольшим. ,
то в первом случаене используют наборы с наименьшим весом, а во втором - с наибольшим.
Строчки образующей матрицы С
представляют собой 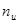 комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй, третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита. комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй, третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита.
Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:
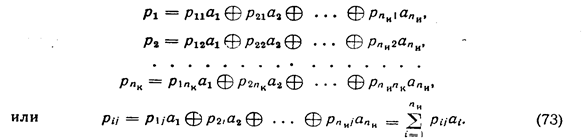
В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:
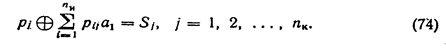
Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом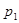 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд 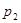 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода 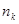 . .
В результате осуществления проверок образуется проверочный вектор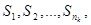 ,
который называют синдромом.
Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор.
,
который называют синдромом.
Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор.
Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н,
которая представляет собой транспонированную матрицу П, дополненную единичной матрицей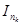 ,
число столбцов которой равно числу проверочныхразрядов кода: ,
число столбцов которой равно числу проверочныхразрядов кода:
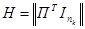 . .
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н
.
Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.
Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы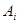 .
В первом столбце второй строки размещается вектор .
В первом столбце второй строки размещается вектор 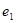 ,
вес которого равен 1. ,
вес которого равен 1.
Остальные позиции второй строки заполняются векторами, полученными в результате суммирования по модулю 2 вектора 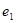 c вектором c вектором 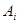 ,
расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор ,
расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор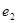 ,
вес которого также равен 1, однако, если вектор ,
вес которого также равен 1, однако, если вектор 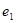 содержит единицу в первом разряде, то содержит единицу в первом разряде, то 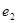 - во втором. В остальные позиции третьей строки записывают суммы - во втором. В остальные позиции третьей строки записывают суммы 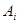 и и 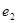 . .
Аналогично поступают до тех пор, пока не будут просуммированы с векторами 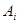 все векторы все векторы 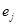 , весом 1, с единицами в каждом из п
разрядов. Затем суммируются по модулю 2 векторы , весом 1, с единицами в каждом из п
разрядов. Затем суммируются по модулю 2 векторы 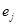 , весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора , весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора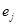 определяет число исправляемых ошибок. Числовекторов определяет число исправляемых ошибок. Числовекторов 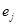 ,
определяется возможным числом неповторяющихся синдромов и равно ,
определяется возможным числом неповторяющихся синдромов и равно 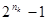 (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор 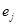 . Векторы . Векторы 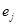 ,
есть векторы ошибок, которые могут быть исправлены данным групповым кодом. ,
есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации 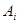 с вектором ошибки с вектором ошибки 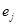 , т. е. к определенной строке кодовой табл.6.1. , т. е. к определенной строке кодовой табл.6.1.
Таблица6.1
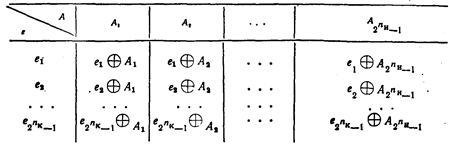
Принятая кодовая комбинация 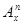 сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок 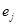 . .
Векторы 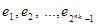 не должны быть равны ни одномуизвекторов не должны быть равны ни одномуизвекторов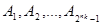 , в противном случае в таблице появились бы нулевые векторы. , в противном случае в таблице появились бы нулевые векторы.
Тривиальные систематические коды.
Код Хэмминга
Систематические коды
представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.
Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее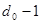 единиц, а сумма по модулю два любых строк не менее единиц, а сумма по модулю два любых строк не менее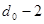 единиц (где единиц (где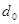 - минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю два строк производящей матрицы во всех возможных сочетаниях. - минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю два строк производящей матрицы во всех возможных сочетаниях.
Код Хэмминга
является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных комбинаций 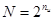 .
При помощи (59) и (60) вычисляются .
При помощи (59) и (60) вычисляются 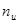 и и 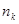 .
Соотношения между .
Соотношения между 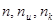 для кода Хэмминга представлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону для кода Хэмминга представлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону 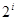 , где , где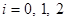 и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т. д. и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т. д.
Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной.
Если эта сумма четна,тозначение контрольного коэффициента - 0, в противном случае - 1.
Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы
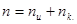
Первой строке соответствует проверочный коэффициент 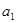 , второй , второй 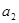 и т.д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. и т.д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. 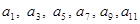 и т. д.; во вторую - коэффициенты, содержащие 1 во втором разряде, т.е. и т. д.; во вторую - коэффициенты, содержащие 1 во втором разряде, т.е. 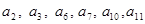 и т.д.; в третью проверку - коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также порядок следования разрядов в полученном двоичном коде. и т.д.; в третью проверку - коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также порядок следования разрядов в полученном двоичном коде.
Если в принятом коде есть ошибка, то результаты проверок по контрольным позициям образуют двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции на обратный.
Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки
Циклические коды
Циклические коды [4,
6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинаций кода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически[13]
, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных
кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.
Идея построения циклических кодов базируется на использовании неприводимых
в поле[14]
двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.
Неприводимые многочлены в теории циклических кодов играют роль образующих
(генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.
Предположим, требуйся закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация - 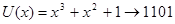 . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен 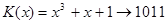 . Затем умножим . Затем умножим 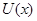 на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени п
степень каждого члена многочлена повысится на на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени п
степень каждого члена многочлена повысится на 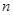 , что эквивалентно приписыванию , что эквивалентно приписыванию 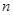 нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени: нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
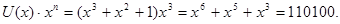
Это делается для того, чтобы впоследствии на месте этих нулей можно было бы записать корректирующие разряды.
Значение корректирующих разрядов находят по результатуотделения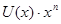 на на 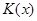 : :
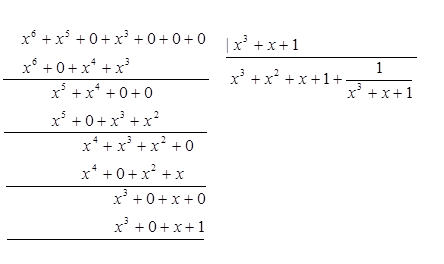 
или
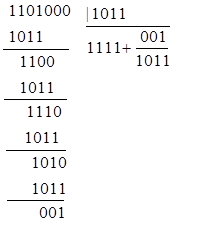
Таким образом,
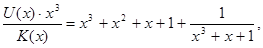
или в общем виде
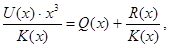 (75) (75)
где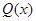 - частное, a - частное, a 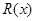 - остаток от деления - остаток от деления 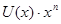 на на 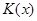 . .
Так как в двоичной арифметике 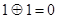 , а значит, , а значит, 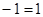 , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида 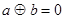 можно записать и как можно записать и как 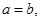 и как и как 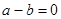 . Все три равенства в данном случае означают, что либо . Все три равенства в данном случае означают, что либо 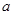 и и 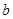 равны 0, либо а
и равны 0, либо а
и 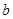 равны 1, т. е. имеют одинаковую четность. равны 1, т. е. имеют одинаковую четность.
Таким образом, выражение (75) можно записать как
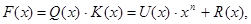 (76) (76)
что в случае нашего примера даст
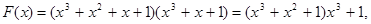
или
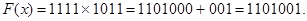
Многочлен 1101001 и есть искомая комбинация, где 1101 - информационная часть, а 001 - контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в данном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имел вид 001).
Таким образом, мы уже знаем два способа образования комбинаций линейных систематических кодов, к которым относятся и интересующие нас циклические коды. Эти способы явились теоретическим основанием для построения кодирующих и декодирующих устройств.
Шифраторы циклических кодов, в том или ином виде, построены по принципу умножения двоичных многочленов. Кодовые комбинации получаются в результате сложения соседних комбинаций по модулю два, что, как мы увидим ниже, эквивалентно умножению первой комбинации на двучлен 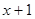 . .
Итак, комбинации циклических кодов можно представлять в виде многочленов, у которых показатели степени 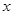 соответствуют номерам разрядов, коэффициенты при х
равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации, которую представляет данный многочлен. Например, соответствуют номерам разрядов, коэффициенты при х
равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации, которую представляет данный многочлен. Например,
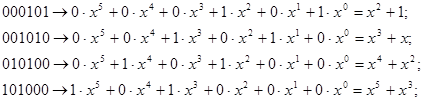
Циклический сдвиг кодовой комбинации аналогичен умножению соответствующего многочлена нах:
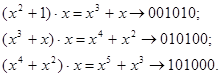
Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при 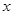 .
В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда. Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентно операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен .
В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда. Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентно операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен 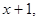 если приведение подобных членов осуществляется по модулю 2: если приведение подобных членов осуществляется по модулю 2:
 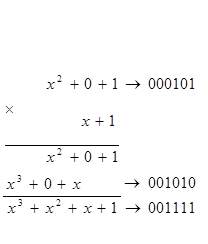
т. е. существует принципиальная возможность получения любой кодовой комбинации циклического кода путем умножения соответствующим образом подобранного образующего многочлена на некоторый другой многочлен.
Однако мало построить циклический код. Надо уметь выделить из него возможные ошибочные разряды, т. е. ввести некоторые опознаватели ошибок, которые выделяли бы ошибочный блок из всех других. Так как циклические коды - блочные, то каждый блок должен иметь свой опознаватель. И тут решающую роль играют свойства образующего многочлена 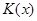 .
Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклических кодов. .
Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклических кодов.
С другой стороны, остатки от деления единицы с нуляминаобразующий многочлен используются для построения циклических кодов (возможность этого видна из выражения (76)).
При делении единицы с нулями на образующий многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулей.Например,
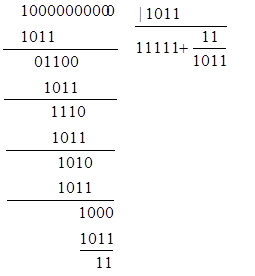 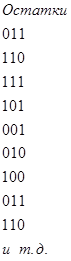
начиная с восьмого, остатки будут повторяться.
Остатки от деления используют для построения образующих матриц, которые, благодаря своей наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матрицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен 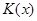 [15]
.
Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой - нули, кроме элементов, расположенных по диагонали справа налево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева направо сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы. [15]
.
Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой - нули, кроме элементов, расположенных по диагонали справа налево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева направо сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
Однако не все остатки от деления единицы с нулями на образующий многочлен могут быть использованы в качестве элементов дополнительной матрицы. Использоваться могут лишь те остатки, вес которых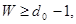 где где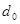 - минимальное кодовое расстояние. Длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов. - минимальное кодовое расстояние. Длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
Строки образующей матрицы представляют собой первые комбинации искомого кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы[16]
.
Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее, чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, в которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен.
Образующая матрица может быть построена также путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга 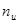 на образующий многочлен. на образующий многочлен.
В заключение предлагаем еще один метод построения циклических кодов. Достоинством этого метода является исключительная простота схемных реализации кодирующих и декодирующих устройств.
Для получения комбинаций циклического кода в этом случае достаточно произвести циклический сдвиг строки образующей матрицы и комбинации, являющейся ее зеркальным отображением. При построении кодов с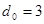 , ,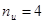 , , 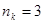 число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при 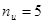 число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы. число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы.
Число ненулевых комбинаций, получаемых в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы,
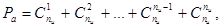 (77) (77)
где 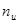 - число информационных разрядов кода[17]
. - число информационных разрядов кода[17]
.
Число ненулевых комбинаций, получаемых в результате циклического сдвига любой строки образующей матрицы и зеркальной ей комбинации,
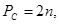 (78) (78)
где 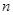 -
длина кодовой комбинации. -
длина кодовой комбинации.
При числе информационных разрядов 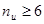 число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий. число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок,
но не указывают непосредственно на место ошибки в циклическом коде.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов “ подгоняется ” под остаток таким образом, что в сумме с остатком она дает исправленную комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок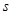 , исправляемых данным кодом (код исправляет 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации - 1 ошибка). , исправляемых данным кодом (код исправляет 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации - 1 ошибка).
Место ошибки в кодовой комбинации не имеет значения. Если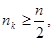 то после определенного количества сдвигов все ошибкиокажутся в зоне “разового” действия образующего многочлена, т. е. достаточно получить один остаток, вес которого то после определенного количества сдвигов все ошибкиокажутся в зоне “разового” действия образующего многочлена, т. е. достаточно получить один остаток, вес которого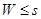 , и этого уже будет достаточно для исправления искаженной комбинации. В этом смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s. , и этого уже будет достаточно для исправления искаженной комбинации. В этом смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
Построение и декодирование конкретных циклических кодов
I. Коды, исправляющие одиночную ошибку,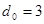 . .
1.Расчет соотношения между контрольными и информационными символами кода
производится на основании выражений (59) - (69).
Если задано число информационных разрядов 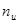 , то число контрольных разрядов , то число контрольных разрядов 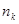 находимиз выражения находимиз выражения
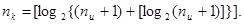
Общее число символов кода
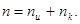
Если задана длина кода 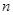 , то число контрольных разрядов , то число контрольных разрядов
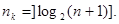
Соотношение числа контрольных и информационных символов для кодов с 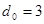 приведены в табл. 3 приложения 9. приведены в табл. 3 приложения 9.
2. Выбор образующего многочлена
производится по таблицам неприводимых двоичных многочленов.
Образующий многочлен 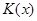 следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов 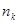 , а число ненулевых членов - не меньше минимальногокодового расстояния , а число ненулевых членов - не меньше минимальногокодового расстояния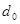 . .
3. Выбор параметров единичной транспонированной матрицы
происходитиз условия, что число столбцов (строк) матрицы определяется числом информационных разрядов, т. е. ранг единичнойматрицы равен 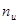 . .
4. Определение элементов дополнительной матрицы
производится по остаткам от деления последней строки транспонированной матрицы (единицы с нулями) на образующий многочлен. Полученные остатки должны удовлетворять следующим требованиям:
а) число разрядов каждого остатка должно быть равно числу контрольных символов 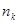 , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена; , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
б) число остатков должно быть не меньше числа строк единичной транспонированной матрицы, т. е. должно быть равно числу информационных разрядов 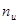 ; ;
в) число единиц каждого остатка, т. е. его вес, должно быть не менее величины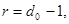 , где , где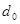 - минимальное кодовое расстояние, не меньшее числа обнаруживаемых ошибок; - минимальное кодовое расстояние, не меньшее числа обнаруживаемых ошибок;
г) количество нулей, приписываемых к единице с нулями при делении ее на выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались условия а), б), в).
5. Образующая матрица
составляется дописыванием элементов дополнительной матрицы справа от единичной транспонированной матрицы либо умножением элементов единичной матрицы на образующий многочлен.
6. Комбинациями искомого кода
являются строки образующей матрицы и все возможные суммы по модулю 2 различных сочетаний строк образующей матрицы.
7. Обнаружение и исправление ошибок
производится по остаткам от деления принятой комбинации на образующий многочлен на образующий многочлен 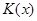 . Если принятая комбинация делится на образующий многочлен без остатка, то код принят безошибочно.
Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции: . Если принятая комбинация делится на образующий многочлен без остатка, то код принят безошибочно.
Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
а) принятую комбинацию делят на образующий многочлен и
б) подсчитывают количество единиц в остатке (вес остатка).
Если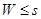 , где s - допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если , где s - допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если 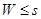 ,
то ,
то
в) производят циклический сдвиг принятой комбинации влево на один разряд. Комбинацию, полученную в результате циклического сдвига, делят на влево на один разряд. Комбинацию, полученную в результате циклического сдвига, делят на 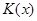 .
Если в результате этого повторного деления .
Если в результате этого повторного деления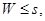 то делимое суммируют с остатком, затем то делимое суммируют с остатком, затем
г) производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делимого с последним остатком. Полученная в результате комбинация уже не содержит ошибок. Если после первого циклического сдвига и последующего деления остаток получается таким, что его вес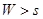 ,
то ,
то
д) повторяют операцию пункта в) до тех пор, пока не будет 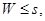 .
В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатком от деления этой комбинации на образующий многочлен, а затем .
В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатком от деления этой комбинации на образующий многочлен, а затем
е) производят циклический сдвиг вправо ровно на столько разрядов,на сколько была сдвинута суммируемая с последним остаткомкомбинация относительно принятой комбинации. В результате получим исправленную комбинацию[18]
.
II. Коды, обнаруживающие трехкратные ошибки,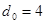 . .
1. Выбор числа корректирующих разрядов
производитсяиз соотношения
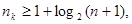
или
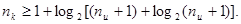
2. Выбор образующего многочлена
производят, исходя из следующих соображений: для обнаружения трехкратной ошибки
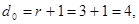
поэтому степень образующего многочлена не может быть меньше четырех; многочлен третьей степени, имеющий •число ненулевых членов больше или равное трем, позволяет обнаруживать все двойные ошибки, многочлен первой степени 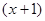 обнаруживает любое количество нечетных ошибок, следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки, а также одну и три, т. е. все трехкратные ошибки. обнаруживает любое количество нечетных ошибок, следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки, а также одну и три, т. е. все трехкратные ошибки.
3. Построение образующей матрицы
производят либо нахождением остатков от деления единицы с нулями на образующий многочлен, либо умножением строк единичной матрицы на образующий многочлен.
4. Остальные комбинации корректирующего кода
находят суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.
5. Обнаружение ошибок
производится по остаткам от деления принятой комбинации на образующий многочлен на образующий многочлен 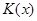 .
Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3. .
Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.
Пример: Исходная кодовая комбинация - 0101111000, принятая - 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки, если известно, что комбинации кода были образованы при помощи многочлена 101111.
Решение:
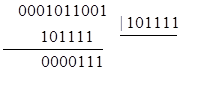
Остаток не нулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.
III. Циклические коды, исправляющие две и большее количество ошибок,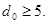
Методика построения циклических кодов с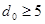 отличается от методики построения циклических кодов с отличается от методики построения циклических кодов с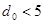 только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем - авторов методики построения циклических кодов с только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем - авторов методики построения циклических кодов с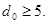 ). ).
Построение образующего многочлена зависит, в основном, от двух параметров: от длины кодового слова п.
и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена, в зависимости от заданных 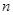 и и 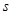 могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже. могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.
Для исправления числа ошибок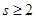 еще не достаточно условия, чтобы между комбинациями кода минимальное кодовое расстояние еще не достаточно условия, чтобы между комбинациями кода минимальное кодовое расстояние 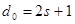 . необходимо также, чтобы длина кода . необходимо также, чтобы длина кода 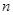 удовлетворяла условию удовлетворяла условию
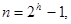 (79) (79)
при этом п
всегда будет нечетным числом. Величинаh
определяет выбор числа контрольных символов 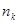 и связана с и связана с 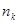 и s следующим соотношением: и s следующим соотношением:
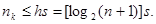 (80) (80)
С другой стороны, число контрольных символов определяется образующим многочленом и равно его степени. При больших значениях h
длина кода п
становится очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h
удобно пользоваться выражением
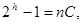 (81) (81)
где 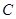 являетсяодним из сомножителей, на которые разлагается число п. являетсяодним из сомножителей, на которые разлагается число п.
Соотношения между 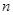 , С иh
могут быть сведены в следующую таблицу , С иh
могут быть сведены в следующую таблицу
| № п/п |
h |
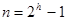 |
C |
1
2
3
4
5
6
7
8
9
10
|
3
4
5
6
7
8
9
10
11
12
|
7
15
31
63
127
255
511
1023
2047
4095
|
1
5; 3
1
7; 3; 3
1
17; 5; 3
7; 3; 7
31; 11; 3
89; 23
3; 3; 5; 7; 13
|
Например, при h
= 10 длина кодовой комбинации может быть равна и 1023 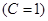 и 341 (С = 3), и 33 (С =31), и 31 (С = 33), понятно, что п
не может быть меньше и 341 (С = 3), и 33 (С =31), и 31 (С = 33), понятно, что п
не может быть меньше 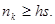 Величина С
влияет на выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются на С. Величина С
влияет на выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются на С.
Построение образующего многочлена 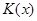 производится при помощи так называемых минимальных многочленов производится при помощи так называемых минимальных многочленов 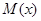 ,
которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и являетсяих наименьшим общим кратным (НОК). Максимальный порядок ,
которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и являетсяих наименьшим общим кратным (НОК). Максимальный порядок 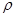 определяет номер последнего из выбираемых табличных минимальных многочленов определяет номер последнего из выбираемых табличных минимальных многочленов
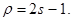 (82) (82)
Порядок многочлена используется при определении числа сомножителей 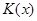 .
Например, если s = 6, то .
Например, если s = 6, то 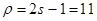 . Так как для построения . Так как для построения 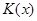 используются только нечетные многочлены, то ими будут: используются только нечетные многочлены, то ими будут: 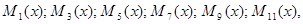 старший из них имеет порядок старший из них имеет порядок 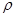 . Как видим, число сомножителей . Как видим, число сомножителей 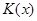 равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена, равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
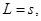 (83) (83)
а старшая степень
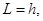 (84) (84)
(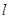 указывает колонку в таблице минимальных многочленов,из которой обычно выбирается многочлен для построения указывает колонку в таблице минимальных многочленов,из которой обычно выбирается многочлен для построения 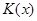 ). ).
Степень образующего многочлена, полученного в результате перемножения выбранных минимальных многочленов,
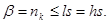 (85) (85)
В общем виде
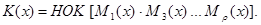 (86) (86)
Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с 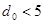 . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с 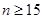 , могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию, полученную после , могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию, полученную после 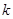 -кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на -кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на 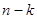 циклических сдвигов. Это целесообразно делать только при циклических сдвигов. Это целесообразно делать только при 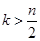 . .
ТЕМА 8. СЖАТИЕ ИНФОРМАЦИИ
Сжатие информации
представляет собой операцию, в результате которой данному коду или сообщению ставится в соответствие более короткий код или сообщение[19]
.
Сжатие информации имеет целью - ускорение и удешевление процессов механизированной обработки, хранения и поиска информации, экономия памяти ЭВМ. При сжатии следует стремиться к минимальной неоднозначности сжатых кодов при максимальной простоте алгоритма сжатия. Рассмотрим наиболее характерные методы сжатия информации.
Сжатие информации делением кода на части, меньшие некоторой наперед заданной величины А,
заключается в том, что исходный код делится на части, меньшие А,
после чего полученные части кода складываются между собой либо по правилам .двоичной арифметики, либо по модулю 2. Например, исходный код 101011010110; A = 4
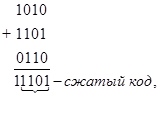 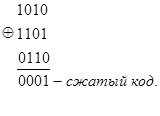
Сжатие информации с побуквенным сдвигом в каждом разряде
[5], как и предыдущий способ, не предусматривает восстановления сжимаемых кодов, а применяется лишь для сокращения адреса либо самого кода сжимаемого слова в памяти ЭВМ.
Предположим, исходное слово «газета» кодируетсякодом, в котором длина кодовой комбинации буквы l
= 8:
Г - 01000111; а - 11110000; з - 01100011; е - 00010111; т - 11011000.
Полный код слова «Газета»
010001111111000001100011000101111101100011110000.
Сжатие осуществляется сложением по модулю 2 двоичных кодов букв сжимаемого слова с побуквенным сдвигом в каждом разряде.

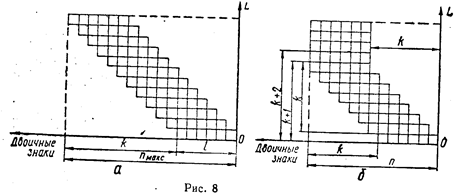
Допустимое количество разрядов сжатого кода является вполне определенной величиной, зависящей от способа кодирования и от емкости ЗУ. Количество адресов, а соответственно максимальное количество слов в выделенном участке памяти машины определяется из следующего соотношения
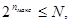 (88) (88)
где 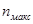 - максимально допустимая длина (количество двоичных разрядов) сжатого кода; N - возможное количество адресов в ЗУ. Если представить процесс побуквенного сдвига в общем виде, как показано на рис. 1, а, то длина сжатого кода - максимально допустимая длина (количество двоичных разрядов) сжатого кода; N - возможное количество адресов в ЗУ. Если представить процесс побуквенного сдвига в общем виде, как показано на рис. 1, а, то длина сжатого кода
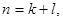
гдеk -
число побуквенных сдвигов; 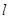 - длина кодовой комбинации буквы. - длина кодовой комбинации буквы.
Так как сдвигаются все буквы, кроме первой, то и число сдвигов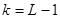 , гдеL -
число букв в слове. Тогда , гдеL -
число букв в слове. Тогда
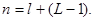
В русском языке наиболее длинные слова имеют 23 - 25 букв. Если принять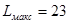 , с условием осуществления побуквенного сдвига с каждым шагом ровно на один разряд, для n и l
могут быть получены следующие соотношения , с условием осуществления побуквенного сдвига с каждым шагом ровно на один разряд, для n и l
могут быть получены следующие соотношения
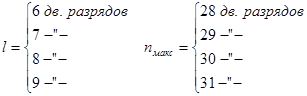
Если значение 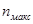 не удовлетворяет неравенству (88),можноконечные буквы слова складывать по модулю 2 без сдвига относительно предыдущей буквы, как это показано на рис 1, б. не удовлетворяет неравенству (88),можноконечные буквы слова складывать по модулю 2 без сдвига относительно предыдущей буквы, как это показано на рис 1, б.
Например, если для предыдущего примера со словом “Газета”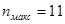 , сжатый код будет иметь вид: , сжатый код будет иметь вид:
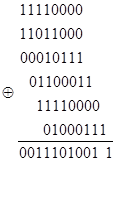
Метод сжатия информации на основе исключения повторения в старших разрядах последующих строк, массивов одинаковых элементов старших разрядов предыдущих строк массивов
основан на том, что в сжатых массивах повторяющиеся элементы старших разрядов заменяются некоторым условным символом.
Очень часто обрабатываемая информация бывает представлена в виде набора однородных массивов, в которых элементы столбцов или строк массивов расположены в нарастающем порядке. Если считать старшими разряды, расположенные левее данного элемента, а младшими - расположенные правее, то можно заметить, что во многих случаях строки матриц отличаются друг от друга в младших разрядах. Если при записи каждого последующего элемента массива отбрасывать все повторяющиеся в предыдущем элементы, например в строке стоящие подряд элементы старших разрядов,то массивы могут быть сокращены от 2 до 10 и более разрядов [2].
Для учета выброшенных разрядов вводится знак раздела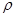 ,
который позволяет отделить элементы в свернутом массиве. В случае полного повторения строк записывается соответствующеколичество ,
который позволяет отделить элементы в свернутом массиве. В случае полного повторения строк записывается соответствующеколичество 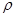 . При развертывании вместознака . При развертывании вместознака 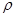 восстанавливаются все пропущенные разряды, которые были до элемента, стоящего непосредственно за восстанавливаются все пропущенные разряды, которые были до элемента, стоящего непосредственно за 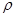 в сжатом тексте. в сжатом тексте.
Для примера рассмотрим следующий массив:
Свернутый массив будет иметь вид:
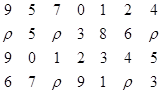
Расшифровка (развертывание) происходит с конца массива. Переход на следующую строку происходит по двум условиям: либо по заполнению строки, либо при встрече 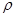 . .
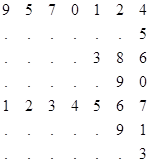
Пропущенные цифры заполняются автоматически по аналогичным разрядам предыдущей строки. Заполнение производится с начала массива. Этот метод можно развить и для свертывания массивов, в которых повторяющиеся разряды встречаются не только с начала строки. Если в строке один повторяющийся участок, то кроме 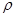 добавляется еще один дополнительный символ К,
означающий конец строки. Расшифровка ведется от К
до К.
Длина строки известна. Нужно, чтобы оставшиеся между K
цифры вместе с пропущенными разрядами составляли полную строку. При этом нам все равно, в каком месте строки выбрасываются повторяющиесяразряды, лишь бы в строке было не более одного участка с повторяющимися разрядами. Например: добавляется еще один дополнительный символ К,
означающий конец строки. Расшифровка ведется от К
до К.
Длина строки известна. Нужно, чтобы оставшиеся между K
цифры вместе с пропущенными разрядами составляли полную строку. При этом нам все равно, в каком месте строки выбрасываются повторяющиесяразряды, лишь бы в строке было не более одного участка с повторяющимися разрядами. Например:

Если в строке есть два повторяющихся участка,то,
используя этот метод, выбрасываем больший.
Процесс развертывания массива осуществляется следующим образом: переход на следующую строку происходит при встрече К
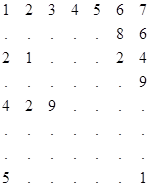
Пропущенные цифры заполняются по аналогичным разрядам предыдущей строки начиная с конца массива.
Если в строке массива несколько повторяющихся участков, томожно вместо 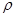 вставлять специальные символы, указывающие на необходимое число пропусков. вставлять специальные символы, указывающие на необходимое число пропусков.
Например, если обозначить количество пропусков, соответственно, Х
-
2;
Y -
3; Z - 5, то исходный и свернутый массивы будут иметь вид:
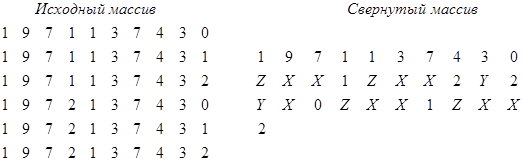
Процесс развертывания массива осуществляется следующим образом: длина строки известна, количество пропусков определяется символами X,
Y, Z
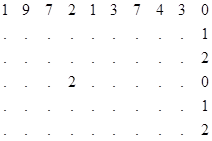
Пропущенные цифры заполняются по аналогичным разрядам предыдущей строки. Условием перехода на следующую строку является заполнение предыдущей строки.
Метод Г. В. Ливинского
основан на том, что в памяти машины хранятся сжатые числа, разрядность которых меньше разрядности реальных чисел. Эффект сжатия достигается за счет того, что последовательности предварительно упорядоченных чисел разбиваются на ряд равных отрезков, внутри которых отсчет ведется не по их абсолютной величине, а от границы предыдущего отрезка. Разрядность чисел, получаемых таким образом, естественно, меньше разрядности соответствующих им реальных чисел [18, 21].
Для размещения в памяти ЭВМ М
кодов, в которых наибольшее из кодируемых чисел равноN,
необходим объем памяти
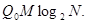
С ростом N
длина кодовой комбинации будет расти как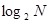 .
Для экономии объема памятиQ,
число .
Для экономии объема памятиQ,
число 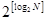 , где выражение в скобках - округленное значение , где выражение в скобках - округленное значение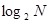 до ближайшего целого числа, разбивают наL
равных частей. Максимальное число в полученном интервале чисел будет не больше до ближайшего целого числа, разбивают наL
равных частей. Максимальное число в полученном интервале чисел будет не больше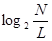 . Величина . Величина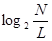 определяет разрядность хранимых чисел, объем памяти дляих хранения будет не больше определяет разрядность хранимых чисел, объем памяти дляих хранения будет не больше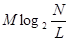 .
Если в памяти ЭВМ хранить адреса границ отрезков и порядковые номера хранимых чисел, отсчитываемых от очередной границы, то .
Если в памяти ЭВМ хранить адреса границ отрезков и порядковые номера хранимых чисел, отсчитываемых от очередной границы, то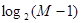 определяет разрядность чисел для выражения номера границы (в последнем интервале должно быть хотя бы одно число); объем памяти для хранения номеров границ будет определяет разрядность чисел для выражения номера границы (в последнем интервале должно быть хотя бы одно число); объем памяти для хранения номеров границ будет 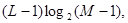 где где 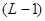 - число границ между отрезками (это число всегда на единицу меньше, чем число отрезков). Общий объем памяти приэтом будет не больше - число границ между отрезками (это число всегда на единицу меньше, чем число отрезков). Общий объем памяти приэтом будет не больше
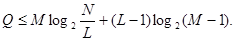 (89) (89)
Чтобы найти, при каких L
выражение (89) принимает минимальное значение, достаточно продифференцировать его по L
и,
приравнять производную к нулю. Нетрудно убедиться, что 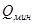 будет при будет при
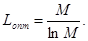 [20]
(90) [20]
(90)
Если подставить значение 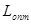 в выражение (89), то получим. значение объема памяти при оптимальном количестве зон, на,
которые разбиваются хранимые в памяти ЭВМ числа, в выражение (89), то получим. значение объема памяти при оптимальном количестве зон, на,
которые разбиваются хранимые в памяти ЭВМ числа,
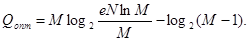 (91) (91)
Для значений 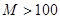 при вычислениях можно пользоваться приближенной формулой при вычислениях можно пользоваться приближенной формулой
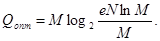 (92) (92)
При поиске информации в памяти ЭВМ прежде всего определяют значение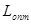 и находят величину интервала между двумя границами и находят величину интервала между двумя границами

Затем определяют, в каком именно из интервалов находится искомое число х
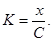
Послеэтого определяется адрес искомого числа как разность между абсолютным значением числа и числом, которое является граничным для данного интервала.
[1]
Первичный алфавит составлен из m1
символов (качественных признаков), при помощи которых записано передаваемое сообщение. Вторичный алфавит состоит из m2
символов, при помощи которых сообщение трансформируется в код.
[2]
Строго говоря, объема информации не существует. Мы вкладываем в этот термин то, что привыкли под этим подразумевать, - количество элементарных символов в принятом (вторичном) сообщении.
[3]
Суть взаимозависимости символов букв алфавита заключается в том, что вероятность появления i-й буквы в любом месте сообщения зависит от того, какие буквы стоят перед ней и после нее, и будет отличаться от безусловной вероятности pi
,
известной из статистических свойств данного алфавита.
' Рассмотрение семантической избыточности не входит в задачи теории информации.
[5]
Здесь и далее под термином «оптимальный код» будем подразумевать коды с практически нулевой избыточностью, так как сравниваем длину кодовой комбинации с энтропией источника сообщений, не учитывая взаимозависимость символов. С учетом взаимозависимости символов эффективность кодирования никогда не будет 100 %, т. е.
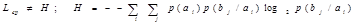
Кроме того, являясь оптимальным с точки зрения скорости передачи информации, код может быть неоптимальным с течки зрения предъявляемых к нему требований помехоустойчивости.
[6]
т—
-число качественных признаков строящегося оптимального кода.
[7]
С основной теоремой кодирования для каналов связи без шумов можно ознакомиться в работе К. Шеннона «Работы по теории информации и кибернетике* либо в популярном изложении в работах [18, 22].
[8]
Рассмотренный принцип заложен в основу мажоритарного декодирования.-корректирующих кодов и известен как метод Бодо—Вердана.
[9]
В какой-то мере исключением из этого правила являются рефлексные коды. В этих кодах последующая комбинация отличается от предыдущей одним символом. В таких, в общем-то безызбыточных кодах, одновременное изменение нескольких символов в принятом сообщении говорит о наличии ошибки. Однако обнаруживать ошибку такие коды могут только в том случае, если кодовые комбинации следуют строго друг за другом. На практике это возможно при передаче информации о плавно изменяющихся процессах.
[10]
В обоих выражениях квадратные скобки означают, что берется округленное значение до ближайшего целого числа в большую сторону. Индекс при 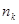 показывает количество исправляемых ошибок, а число в круглых скобках при индексе - число обнаруживаемых ошибок. показывает количество исправляемых ошибок, а число в круглых скобках при индексе - число обнаруживаемых ошибок.
[11]
Условие верхней и нижней границ для максимально допустимого числа информационных разрядов может быть записано следующим образом:
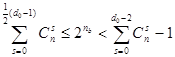 . .
[12]
' Оптимальным корректирующим кодом для симметричного канала называется групповой код, при использовании которого вероятность ошибки не больше, чеу при использовании лю5ого другого кода с такими же п„ и Лц [1, 2, б]. У этихкодов критерий оптимальности не имеет ничего общего с критерием оптимальности ОНК.
[13]
Практически», так как контрольные символы циклических кодов, построенных путем простого перемножения многочленов, могут оказаться в произвольном месте кодовой комбинации.
[14]
Упрощенно, множество элементов принадлежит к одному полю, если над ними можно производить операции сложения и умножения по правилам данного поля, при этом сложение и умножение должны подчиняться дистрибутивному закону 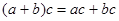 для всех для всех 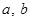 и и 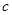 . .
[15]
О возможности представления линейного кода в виде единичной и некоторой дополнительной матрицы см., например, [22, с. 408, 409].
[16]
Следует сказать, что не все циклические коды могут быть полученытакимпростым способом, однако не будем пока усложнять изложение.
[17]
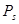 можно определятьи по формуле
можно определятьи по формуле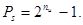
[18]
Коды сd0
= 2, обнаруживающие одиночную ошибку, здесь сознательно не рассматриваются, так как они не имеют практического значения. В двоичных кодах всегда проще подобрать контрольный символ 0 или 1 таким образом, чтобы сумма единиц в кодовом слове была четной, чем строить циклический код для получения того же результата.
[19]
Кодирование от сжатия отличается тем, что коды почти всегда длиннее кодируемых сообщений, так как число качественных признаков вторичного алфавита (кода) обычно не бывает больше числа качественных признаков первичного алфавита (кодируемых сообщений). Говоря «сжатый код», будем иметь в виду комбинацию, представляющую кодируемое понятие после процедуры сжатия.
[20]
При M<100 следует братьболее точное выражение для  , а именно: , а именно: 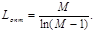
|