№506 На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l = 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin
пленки, если показатель преломления материала пленки n = 1,4.
Дано: Решение:
l = 500 нм= В условии не указано, что пленка нанесена на стеклянную
=500*10-9 м
пластину. Поэтому оптическая разница хода световых волн,
 n = 1,4 возникающая при отражении монохроматического света от
dmin
- ? от тонкой пленки: Δ=2dncosi2
+λ/2 (1), где
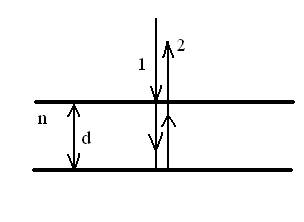
d – толщина пленки;
n – показатель преломления;
i2
– угол преломления света в пленке, i2
=0;
λ/2 – добавочная разность хода, возникающая из-за отражения от оптически более плотной среды.
Условие максимума: Δ =kλ (2)
(1)=(2) 2dn+λ/2=kλ
2dn=(λ/2)*(2k-1)
d=(λ/4n)*(2k-1)
dmin
приk=1 dmin
=λ/4n=(500*10-9
)/(4*1.4)=89,3*10-9
м=89,3нм
Ответ: dmin
= 89,3нм
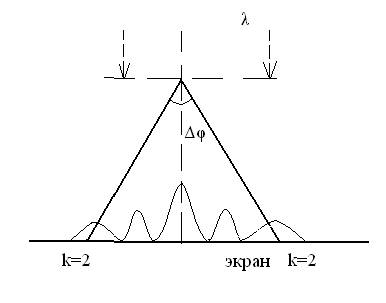
№516 На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Dj = 16°. Определить длину волны l света, падающего на решетку.
Дано: Решение:
n=100 штр/мм= Условие наблюдения максимума на дифракционной решетке
=100000 штр/м dsinφ=kλ (1), где
k=2 k – порядок максимума;
 Δφ=16° φ – угол дифракции.
λ - ? φ=Δφ/2 (2) – в силу симметрии максимумов
d=1/n (3) – постоянная (период решетки)
Тогда (1) перепишется: (1/n)sin(Δφ/2)= kλ (4)
λ=(1/kn)sin(Δφ/2)=(1/105
*2)sin8°=6.96*10-7
м
Ответ: λ=6.96*10-7
м
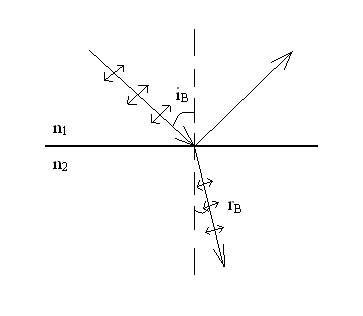
№526. Пучок света переходит из жидкости в стекло. Угол падения i пучка равен 60°, угол преломления r = 50°. При каком угле падения iв
пучок света, отраженный от границы раздела этих сред, будет максимально поляризован?
Дано: Решение:
i=60° Согласно закону Брюстера, пучок света максимально поляризован,
 r=50° если тангенс угла падения iВ
: tgiВ
=n21
(1), где
iВ
- ? n21
– относительный показатель преломления среды.
Найдем n21
из закона преломления
sini/sinr= n2
/ n1
= n21
(2), подставив в первое уравнение получаем
tg iВ
= sin i/sin r iВ
=arctg(sin60°/sin50°)=48,5°
Ответ: iВ
=48,5°
№536 Муфельная печь, потребляющая мощность Р = 1 кВт, имеет отверстие площадью S = 100 см2
. Определить долю h мощности, рассеиваемой стенки печи, если температура ее внутренней поверхности равна 1 кК.
Дано: Решение:
Р=1 кВт= Излучаемая печью мощность P':
=103
Вт Р'=ReS, где Re – излучательность абсолютно черного тела.
S=100 см2
= Согласно закону Стефана-Больцмана:
=10-2 м2
Re=ςТ4
, где ς=5,68*10-8
Вт/м2
К4
– постоянная Стефана-Больцмана.
Т=1 кК= Тогда доля рассеиваемой мощности η:
 =103
К η=1-(Р'/Р)=1-(ςТ4
S/P)=1-(5,67*10-8
*(103
)4
*10-2
/103
)=0,43
η - ?
Ответ: η=0,43 или 43%
№546 На поверхность металла падает монохроматический свет с длиной волны l = 0,1 мкм. Красная граница фотоэффекта lк
= 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
Дано: Решение:
l=0,1 мкм= Согласно уравнению Эйнштейна для внешнего фотоэффекта
=10-7 м (закон сохранения энергии):
hυ=Aвых
+Tmax
(1), где
lк
=0,3 мкм= hυ=hc/λ (2) – энергия падающего кванта излучения;
 =3*10-7 м
h=6,63*10-34
Дж*с – постоянная Планка;
k - ? с=3*108
м/с – скорость света;
Авых
– работа выхода электронов из метала Авых
=hc/lк
(3);
Tmax
– максимальная кинетическая энергия фотоэлектронов.
Доля энергии фотона k на сообщение кинетической энергии
k= Tmax
/(hc/λ) (4)
(1), с условием (2),(3) переписывается hc/λ= hc/lк
+Tmax
(5)
Tmax
=hc(1/λ-1/lк
)
(6) подставляем в (4) и получаем
k= (hc(1/λ-1/lк
))/(hc/λ)= λ(1/λ-1/lк
)=10-7
(1/10-7
-1/(3*10-7
))=0,67
Ответ: k=0,67 или 67%
№556 Найти дефект массы, энергию связи и удельную энергию связи ядра атома углерода 12
6
С.
Дано: Решение:
 12
6
С Дефект массы Δm: Δm=Zmp
+(A-Z)mn
-me
(1)
Δm - ? Z=6 – число протонов (зарядовое число);
Есв
- ? A-Z=12-6=6 – число нейтронов.
εуд
- ? (1) в другом виде Δm=ZmH
+(A-Z)mn
-ma
(2), где
ma
=12 а.e.m. – масса атома;
mH
= 1,00783 а.e.m.
mn
=1,00867 а.e.m. – масса нейтрона.
Δm=(6*1,00783+6*1,00867)-12,00000=0,099 а.e.m.;
Энергия связи Есв
=931Δm МэВ
Есв
=931*0,099=92,17 МэВ;
Удельная энергия связи εуд
= Есв
/А
εуд
=92,17/12=7,68 МэВ/нуклон.
Ответ: Δm=0,099 а.e.m.
Есв
=92,17 МэВ
εуд
=7,68 МэВ/нуклон
№566 Активность А некоторого изотопа за время t = 10 сут уменьшилась на 20%. Определить период полураспада Т1/2
этого изотопа.
Дано: Решение:
ΔА/А0
=0,2 Согласно закону радиоактивного распада, активность уменьшается
t=10 сут по закону А=А0
е-λ
t
(1), где
Т1/2
- ? А0
– начальная активность изотопа при t=0;
А – активность изотопа через время t;
λ – постоянная радиоактивного распада.
λ=ln2/Т1/2
(2), где Т1/2
– период полураспада.
А=А0
-ΔА=А0
-0,2А0
=0,8А0
(3)
(2) и (3) уравнения подставляем в (1) и получаем
0,8А0
= А0
е-
ln2/T *t
ln0,8=-(ln2/Т1/2
*t) откуда Т1/2
=-ln2*t/ln0,8
Т1/2
=- ln2/ln0,8*10=31 cут.
Ответ: Т1/2
=31 cут
№576 Тепловая мощность ядерного реактора 10000 кВт. Какое количество 235
92
U будет израсходовано реактором за сутки? При каждом распаде выделяется энергия 200 МэВ.
Дано: Решение:
t=1 сут= Мощность ядерного реактора P=E/t (1), где
=24*3600 с Е – энергия, выделившаяся при распаде урана массы m
Р=10000 кВт= E= ε0
N (2), где N – количество распавшихся атомов
=107
Вт N=m/μ*NA
(3), где
ε0
=200МэВ μ=235*10-3
кг/моль – молярная масса
 235
92
UNA
=6,02*1023
моль-1
– постоянная Авогадро
m - ? Тогда (2) принимает вид: Е= ε0
m/μ*NA
(4)
Подставляем (4) уравнение в (1), в результате поучаем
P=ε0
mNA
/μt (5)
m=Pμt/ ε0
NA
(6) – масса 1эВ=1,6*10-19
Дж
m=107
*235*10-3
*24*3600/(200*106
*1,6*10-19
*6,02*1023
)=10,5*10-3
кг=10,5 г.
Ответ:m=10,5 г
|
